31.九年级数学(下)第二十七章 相似专题卷A——核心考点归纳一点通(含答案)
文档属性
| 名称 | 31.九年级数学(下)第二十七章 相似专题卷A——核心考点归纳一点通(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 379.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 19:52:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
31.九年级数学(下)第27章《相似》专题卷A——核心考点归纳一点通
核心考点1 平行线分线段成比例定理
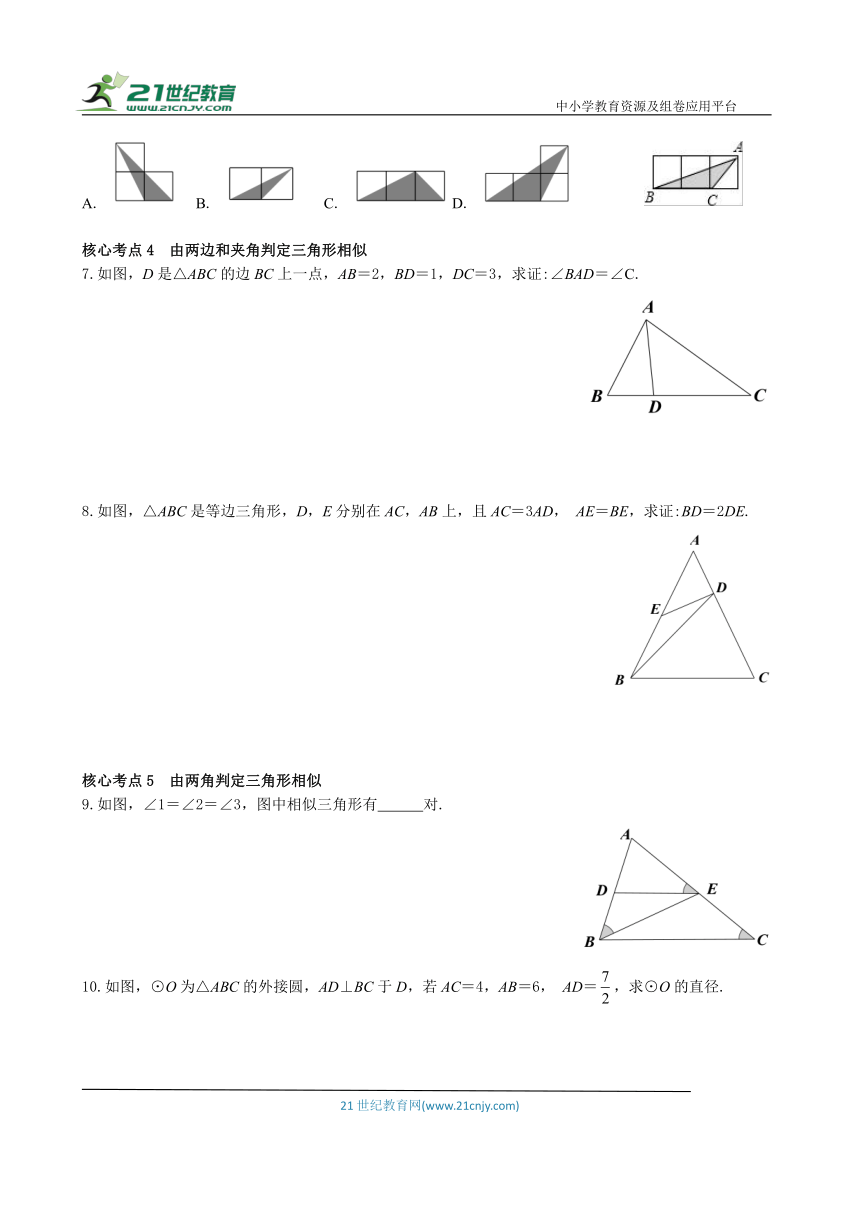
1.已知AB//CD//EF,下列结论正确的是( )
A. B. C. D.
2.如图,已知l1//l2//l3,AB=3,DE=2,DF=5,则BC= .
核心考点2利用 平行线判定三角形相似
3.如图,ABCD中,EF//AD,EF交AC于点G,则图中与△AEG相似的三角形有 .
4.如图,△ABC中,D是AB上一点,DF//BC,延长BC至E,使CE=BC,DE交AC于G,
求证:AD·EG=AB·DG.
核心考点3 利用三边的比判定三角形相似
5.△ABC和△DEF中,AB=4,BC=5,CA=8,DE=15,EF=12,FD=24,则△ABC和△DEF (填“相似” 或“不相似”).
6.下图中的小正方形的边长均为1,则选项中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
核心考点4 由两边和夹角判定三角形相似
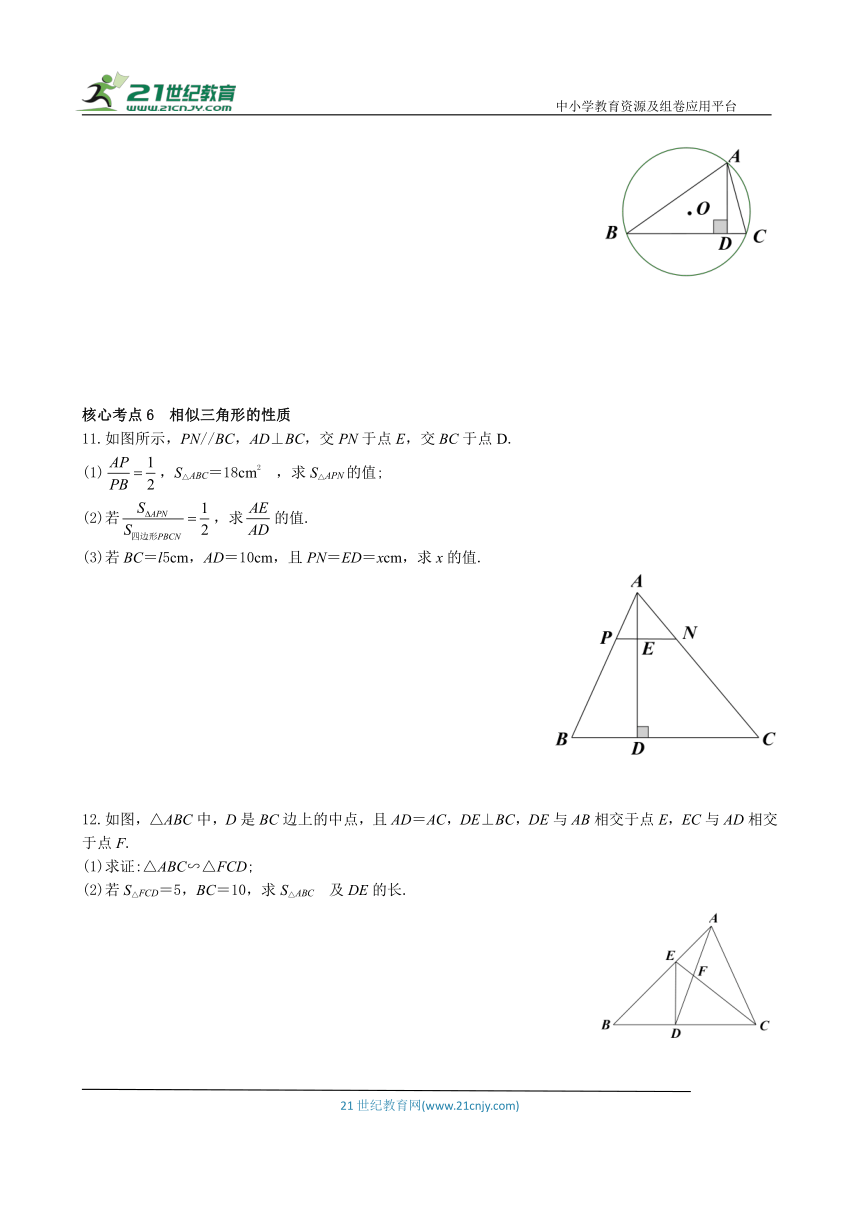
7.如图,D是△ABC的边BC上一点,AB=2,BD=1,DC=3,求证:∠BAD=∠C.
8.如图,△ABC是等边三角形,D,E分别在AC,AB上,且AC=3AD, AE=BE,求证:BD=2DE.
核心考点5 由两角判定三角形相似
9.如图,∠1=∠2=∠3,图中相似三角形有 对.
10.如图,⊙O为△ABC的外接圆,AD⊥BC于D,若AC=4,AB=6, AD=,求⊙O的直径.
核心考点6 相似三角形的性质
11.如图所示,PN//BC,AD⊥BC,交PN于点E,交BC于点D.
(1),S△ABC=18cm2 ,求S△APN的值;
(2)若,求的值.
(3)若BC=l5cm,AD=10cm,且PN=ED=xcm,求x的值.
12.如图,△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若S△FCD=5,BC=10,求S△ABC 及DE的长.
核心考点7 相似三角形的实际应用
(一)利用影子长测量物体高度
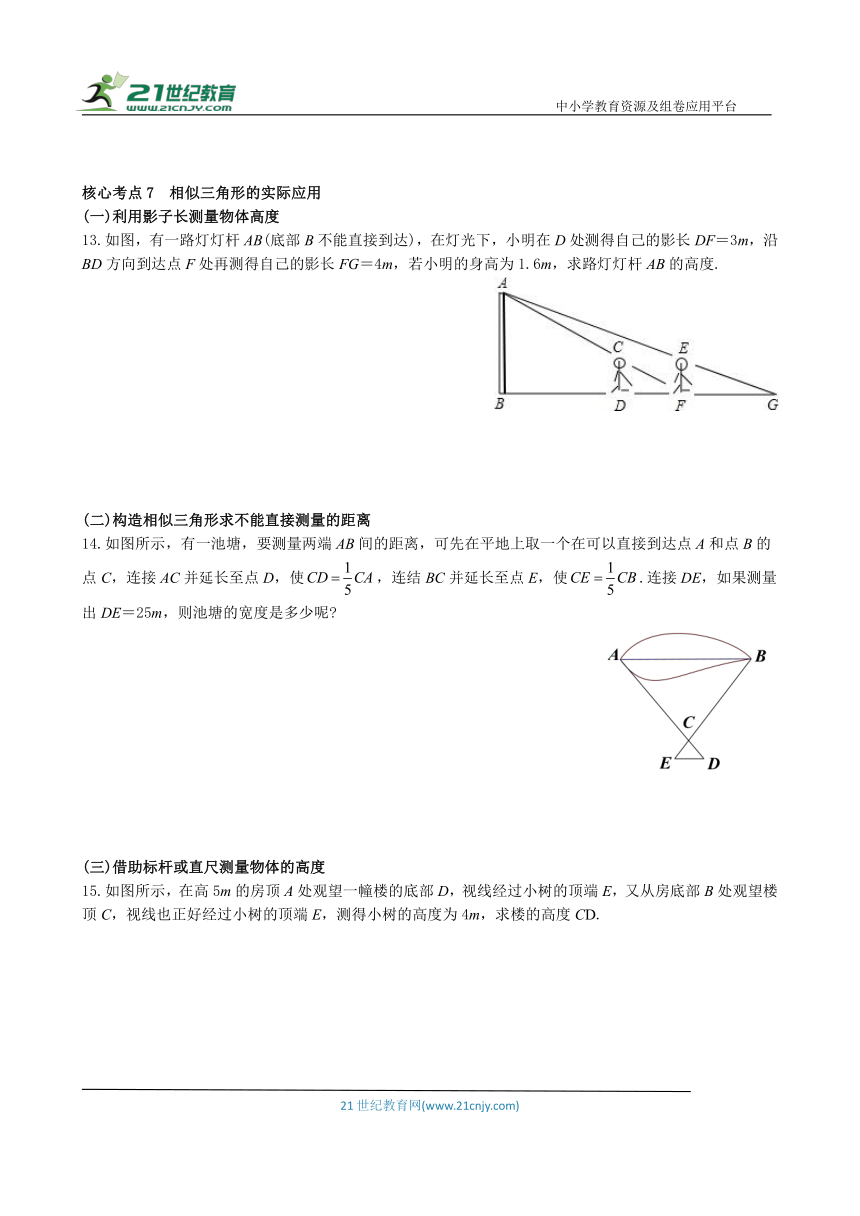
13.如图,有一路灯灯杆AB(底部B不能直接到达),在灯光下,小明在D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m,若小明的身高为1.6m,求路灯灯杆AB的高度.
(二)构造相似三角形求不能直接测量的距离
14.如图所示,有一池塘,要测量两端AB间的距离,可先在平地上取一个在可以直接到达点A和点B的点C,连接AC并延长至点D,使,连结BC并延长至点E,使.连接DE,如果测量出DE=25m,则池塘的宽度是多少呢
(三)借助标杆或直尺测量物体的高度
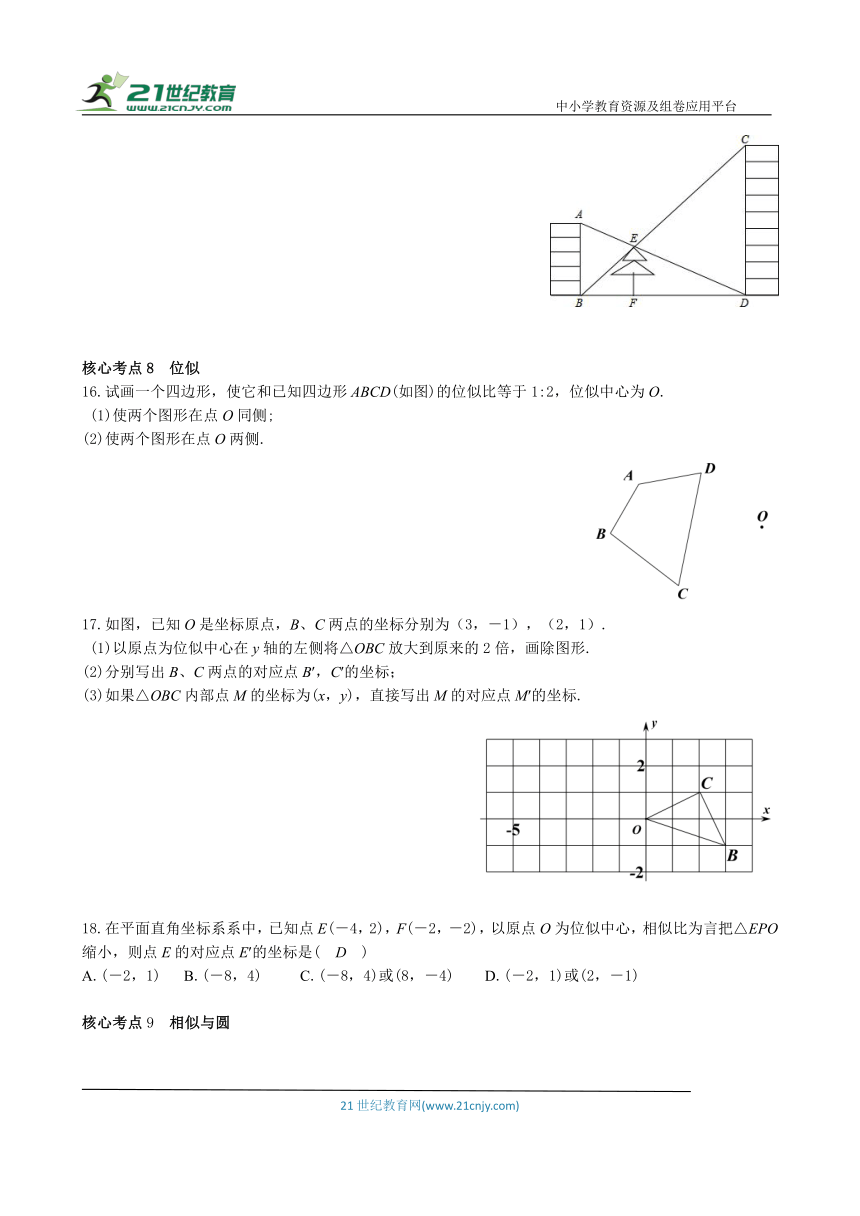
15.如图所示,在高5m的房顶A处观望一幢楼的底部D,视线经过小树的顶端E,又从房底部B处观望楼顶C,视线也正好经过小树的顶端E,测得小树的高度为4m,求楼的高度CD.
核心考点8 位似
16.试画一个四边形,使它和已知四边形ABCD(如图)的位似比等于1:2,位似中心为O.
(1)使两个图形在点O同侧;
(2)使两个图形在点O两侧.
17.如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).
(1)以原点为位似中心在y轴的左侧将△OBC放大到原来的2倍,画除图形.
(2)分别写出B、C两点的对应点B,C的坐标;
(3)如果△OBC内部点M的坐标为(x,y),直接写出M的对应点M的坐标.
18.在平面直角坐标系系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为言把△EPO缩小,则点E的对应点E的坐标是( D )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
核心考点9 相似与圆
19.如图,△ABC内接于⊙O,BD是⊙O的直径,AC,BD相交于点E, AC=BC,AD=5,DE=2,求⊙O的半径.
20.如图,△BCD中,DB=DC,点O在BC上,过B,D两点的⊙O与CD交于点E,若E为CD的中点,求的值.
核心考点10 相似与二次函数
21.如图,抛物线y=x2-3x-4交x轴交于A,B两点。且过点C(2,m),点G在线段AC上运动(不与A,C重合),若ABG=ACB,求点G的坐标.
22. 如图,抛物线y=x2-2x-1交y轴于点P,且经过点E(3,2),点F为抛物线上一点,且PFPE,求点F的坐标.
核心考点11 相似与反比例函数
23.如图,过原点O的直线与双曲线交于点A,与双曲线交于点B,若OB=2OA,则k的值是 .
24.如图,若双曲线与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,且0C=3BD,则k的值是 .
31.九年级数学(下)第27章《相似》专题卷A——核心考点归纳一点通
核心考点1 平行线分线段成比例定理
1.已知AB//CD//EF,下列结论正确的是( A )
A. B. C. D.
2.如图,已知l1//l2//l3,AB=3,DE=2,DF=5,则BC=
核心考点2利用 平行线判定三角形相似
3.如图,ABCD中,EF//AD,EF交AC于点G,则图中与△AEG相似的三角形有△ABC,△CFG,△ADC_.
4.如图,△ABC中,D是AB上一点,DF//BC,延长BC至E,使CE=BC,DE交AC于G,求证:AD·EG=AB·DG.
证明:∵DF//BC,∴△ADF∽△ABC,∴,
∵DF//CE,∴△GDF∽△GEC,,
∵CE=BC.∴AD·EG=AB·DG.
核心考点3 利用三边的比判定三角形相似
5.△ABC和△DEF中,AB=4,BC=5,CA=8,DE=15,EF=12,FD=24,则△ABC和△DEF 相似 (填“相似” 或“不相似”).
6.下图中的小正方形的边长均为1,则选项中的三角形(阴影部分)与△ABC相似的是( B )
A. B. C. D.
核心考点4 由两边和夹角判定三角形相似
7.如图,D是△ABC的边BC上一点,AB=2,BD=1,DC=3,求证:∠BAD=∠C.
证明:∵,∠B =∠B,∴△BAD∽△BCA,∴∠BAD=∠C.
8.如图,△ABC是等边三角形,D,E分别在AC,AB上,且AC=3AD, AE=BE,求证:BD=2DE.
证明:∵,∠A=∠C,∴AED∽△CBD,
∴.∴BD=2DE.
核心考点5 由两角判定三角形相似
9.如图,∠1=∠2=∠3,图中相似三角形有_ 4 对.
10.如图,⊙O为△ABC的外接圆,AD⊥BC于D,若AC=4,AB=6, AD=,求⊙O的直径.
解:作直径AE,连接BE,易证△ABE∽△ADC,.AB·AC=AD·AE,∴AE= .
核心考点6 相似三角形的性质
11.如图所示,PN//BC,AD⊥BC,交PN于点E,交BC于点D.
(1),S△ABC=18cm2 ,求S△APN的值;
(2)若,求的值.
(3)若BC=l5cm,AD=10cm,且PN=ED=xcm,求x的值.
解:(1)2cm2 ;
(2);
(3)6cm.
12.如图,△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若S△FCD=5,BC=10,求S△ABC 及DE的长.
解:(1)证∠B=∠DCF,∠ADC=∠ACB即可.
(2)∵,∴S△ABC=20.作AM⊥BC于M.∴BC·AM=20,.AM=4,易证DM=CM,∴,∴
核心考点7 相似三角形的实际应用
(一)利用影子长测量物体高度
13.如图,有一路灯灯杆AB(底部B不能直接到达),在灯光下,小明在D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m,若小明的身高为1.6m,求路灯灯杆AB的高度.
解:∵△ABF∽△CDF,∴.△ABG∽△EFG.
∴.∴BD=9,AB=6.4.
(二)构造相似三角形求不能直接测量的距离
14.如图所示,有一池塘,要测量两端AB间的距离,可先在平地上取一个在可以直接到达点A和点B的点C,连接AC并延长至点D,使,连结BC并延长至点E,使.连接DE,如果测量出DE=25m,则池塘的宽度是多少呢
解:∵,. ∴.
又∵∠ECD=∠BCA,∴△ECD∽△BCA.
∴.
∵ED =25m,∴AB=255=125(m),
故池塘的宽度是125m.
(三)借助标杆或直尺测量物体的高度
15.如图所示,在高5m的房顶A处观望一幢楼的底部D,视线经过小树的顶端E,又从房底部B处观望楼顶C,视线也正好经过小树的顶端E,测得小树的高度为4m,求楼的高度CD.
解:∵,∴.∵,∴,∴CD = 20m.
核心考点8 位似
16.试画一个四边形,使它和已知四边形ABCD(如图)的位似比等于1:2,位似中心为O.
(1)使两个图形在点O同侧;
(2)使两个图形在点O两侧.
17.如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).
(1)以原点为位似中心在y轴的左侧将△OBC放大到原来的2倍,画除图形.
(2)分别写出B、C两点的对应点B,C的坐标;
(3)如果△OBC内部点M的坐标为(x,y),直接写出M的对应点M的坐标.
解:(1)略
(2)B(-6,2),C(-4,-2),
(3)M(-2x,-2y).
18.在平面直角坐标系系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为言把△EPO缩小,则点E的对应点E的坐标是( D )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
核心考点9 相似与圆
19.如图,△ABC内接于⊙O,BD是⊙O的直径,AC,BD相交于点E, AC=BC,AD=5,DE=2,求⊙O的半径.
解:连接CO并延长交AB于H,∵AC=BC,.∴ CH⊥AB,
∵BD是⊙O的直径,DA⊥AB,∴CH//DA,
∴△COE∽△ADE,∴,
设⊙O的半径为r,则OC=OD=r,OE=r-2,
∴解得.
20.如图,△BCD中,DB=DC,点O在BC上,过B,D两点的⊙O与CD交于点E,若E为CD的中点,求的值.
解:作OH⊥DE于H,作ON⊥BD于N.
设DH=EH=x,则CE=2x,BN=DN=2x,
∵.
核心考点10 相似与二次函数
21.如图,抛物线y=x2-3x-4交x轴交于A,B两点。且过点C(2,m),点G在线段AC上运动(不与A,C重合),若ABG=ACB,求点G的坐标.
解:易求A(-1,0),B(4,0),C(2,-6),可来AC解新式为y=-2x-2,
由△ABG∽△ACB,,AB=5,AC=,,
设G(t,-2t-2),则,,∴
22. 如图,抛物线y=x2-2x-1交y轴于点P,且经过点E(3,2),点F为抛物线上一点,且PFPE,求点F的坐标.
解:分别过E,F作y轴垂线FG,EM,垂足分别为M,G,
∴△MEP∽△GPF,,
又MP=3,ME=3,∴PG=GF,
设F(t,t2-2t-1),GF=t,PG=-1-(t2-2t-1),
t=-1-(t2-2t-1),t1=0(舍去),t2=1,∴F(1,-2).
注:此题还可延长PF交工轴于N,由P,N坐标求PF解析式,后求点F坐标。
核心考点11 相似与反比例函数
23.如图,过原点O的直线与双曲线交于点A,与双曲线交于点B,若OB=2OA,则k的值是 .
解:作AE⊥x轴于E,BF⊥x轴于F.∴△AOE∽△BOF,又OB=2OA,. BF=2AE,FO=2EO,∴k=4.
24.如图,若双曲线与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,且0C=3BD,则k的值是 .
解:过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F,∠AOB=ABO=60°,
设BF=x,则DF=, △COE∽△DBF,
∵OC=3BD,∴OE=3BF=3x,CE=3DF=
∴C(3x,),D(5-x,),
∴,x1=0(舍去),x2=,.
21世纪教育网(www.21cnjy.com)
31.九年级数学(下)第27章《相似》专题卷A——核心考点归纳一点通
核心考点1 平行线分线段成比例定理
1.已知AB//CD//EF,下列结论正确的是( )
A. B. C. D.
2.如图,已知l1//l2//l3,AB=3,DE=2,DF=5,则BC= .
核心考点2利用 平行线判定三角形相似
3.如图,ABCD中,EF//AD,EF交AC于点G,则图中与△AEG相似的三角形有 .
4.如图,△ABC中,D是AB上一点,DF//BC,延长BC至E,使CE=BC,DE交AC于G,
求证:AD·EG=AB·DG.
核心考点3 利用三边的比判定三角形相似
5.△ABC和△DEF中,AB=4,BC=5,CA=8,DE=15,EF=12,FD=24,则△ABC和△DEF (填“相似” 或“不相似”).
6.下图中的小正方形的边长均为1,则选项中的三角形(阴影部分)与△ABC相似的是( )
A. B. C. D.
核心考点4 由两边和夹角判定三角形相似
7.如图,D是△ABC的边BC上一点,AB=2,BD=1,DC=3,求证:∠BAD=∠C.
8.如图,△ABC是等边三角形,D,E分别在AC,AB上,且AC=3AD, AE=BE,求证:BD=2DE.
核心考点5 由两角判定三角形相似
9.如图,∠1=∠2=∠3,图中相似三角形有 对.
10.如图,⊙O为△ABC的外接圆,AD⊥BC于D,若AC=4,AB=6, AD=,求⊙O的直径.
核心考点6 相似三角形的性质
11.如图所示,PN//BC,AD⊥BC,交PN于点E,交BC于点D.
(1),S△ABC=18cm2 ,求S△APN的值;
(2)若,求的值.
(3)若BC=l5cm,AD=10cm,且PN=ED=xcm,求x的值.
12.如图,△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若S△FCD=5,BC=10,求S△ABC 及DE的长.
核心考点7 相似三角形的实际应用
(一)利用影子长测量物体高度
13.如图,有一路灯灯杆AB(底部B不能直接到达),在灯光下,小明在D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m,若小明的身高为1.6m,求路灯灯杆AB的高度.
(二)构造相似三角形求不能直接测量的距离
14.如图所示,有一池塘,要测量两端AB间的距离,可先在平地上取一个在可以直接到达点A和点B的点C,连接AC并延长至点D,使,连结BC并延长至点E,使.连接DE,如果测量出DE=25m,则池塘的宽度是多少呢
(三)借助标杆或直尺测量物体的高度
15.如图所示,在高5m的房顶A处观望一幢楼的底部D,视线经过小树的顶端E,又从房底部B处观望楼顶C,视线也正好经过小树的顶端E,测得小树的高度为4m,求楼的高度CD.
核心考点8 位似
16.试画一个四边形,使它和已知四边形ABCD(如图)的位似比等于1:2,位似中心为O.
(1)使两个图形在点O同侧;
(2)使两个图形在点O两侧.
17.如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).
(1)以原点为位似中心在y轴的左侧将△OBC放大到原来的2倍,画除图形.
(2)分别写出B、C两点的对应点B,C的坐标;
(3)如果△OBC内部点M的坐标为(x,y),直接写出M的对应点M的坐标.
18.在平面直角坐标系系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为言把△EPO缩小,则点E的对应点E的坐标是( D )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
核心考点9 相似与圆
19.如图,△ABC内接于⊙O,BD是⊙O的直径,AC,BD相交于点E, AC=BC,AD=5,DE=2,求⊙O的半径.
20.如图,△BCD中,DB=DC,点O在BC上,过B,D两点的⊙O与CD交于点E,若E为CD的中点,求的值.
核心考点10 相似与二次函数
21.如图,抛物线y=x2-3x-4交x轴交于A,B两点。且过点C(2,m),点G在线段AC上运动(不与A,C重合),若ABG=ACB,求点G的坐标.
22. 如图,抛物线y=x2-2x-1交y轴于点P,且经过点E(3,2),点F为抛物线上一点,且PFPE,求点F的坐标.
核心考点11 相似与反比例函数
23.如图,过原点O的直线与双曲线交于点A,与双曲线交于点B,若OB=2OA,则k的值是 .
24.如图,若双曲线与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,且0C=3BD,则k的值是 .
31.九年级数学(下)第27章《相似》专题卷A——核心考点归纳一点通
核心考点1 平行线分线段成比例定理
1.已知AB//CD//EF,下列结论正确的是( A )
A. B. C. D.
2.如图,已知l1//l2//l3,AB=3,DE=2,DF=5,则BC=
核心考点2利用 平行线判定三角形相似
3.如图,ABCD中,EF//AD,EF交AC于点G,则图中与△AEG相似的三角形有△ABC,△CFG,△ADC_.
4.如图,△ABC中,D是AB上一点,DF//BC,延长BC至E,使CE=BC,DE交AC于G,求证:AD·EG=AB·DG.
证明:∵DF//BC,∴△ADF∽△ABC,∴,
∵DF//CE,∴△GDF∽△GEC,,
∵CE=BC.∴AD·EG=AB·DG.
核心考点3 利用三边的比判定三角形相似
5.△ABC和△DEF中,AB=4,BC=5,CA=8,DE=15,EF=12,FD=24,则△ABC和△DEF 相似 (填“相似” 或“不相似”).
6.下图中的小正方形的边长均为1,则选项中的三角形(阴影部分)与△ABC相似的是( B )
A. B. C. D.
核心考点4 由两边和夹角判定三角形相似
7.如图,D是△ABC的边BC上一点,AB=2,BD=1,DC=3,求证:∠BAD=∠C.
证明:∵,∠B =∠B,∴△BAD∽△BCA,∴∠BAD=∠C.
8.如图,△ABC是等边三角形,D,E分别在AC,AB上,且AC=3AD, AE=BE,求证:BD=2DE.
证明:∵,∠A=∠C,∴AED∽△CBD,
∴.∴BD=2DE.
核心考点5 由两角判定三角形相似
9.如图,∠1=∠2=∠3,图中相似三角形有_ 4 对.
10.如图,⊙O为△ABC的外接圆,AD⊥BC于D,若AC=4,AB=6, AD=,求⊙O的直径.
解:作直径AE,连接BE,易证△ABE∽△ADC,.AB·AC=AD·AE,∴AE= .
核心考点6 相似三角形的性质
11.如图所示,PN//BC,AD⊥BC,交PN于点E,交BC于点D.
(1),S△ABC=18cm2 ,求S△APN的值;
(2)若,求的值.
(3)若BC=l5cm,AD=10cm,且PN=ED=xcm,求x的值.
解:(1)2cm2 ;
(2);
(3)6cm.
12.如图,△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若S△FCD=5,BC=10,求S△ABC 及DE的长.
解:(1)证∠B=∠DCF,∠ADC=∠ACB即可.
(2)∵,∴S△ABC=20.作AM⊥BC于M.∴BC·AM=20,.AM=4,易证DM=CM,∴,∴
核心考点7 相似三角形的实际应用
(一)利用影子长测量物体高度
13.如图,有一路灯灯杆AB(底部B不能直接到达),在灯光下,小明在D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m,若小明的身高为1.6m,求路灯灯杆AB的高度.
解:∵△ABF∽△CDF,∴.△ABG∽△EFG.
∴.∴BD=9,AB=6.4.
(二)构造相似三角形求不能直接测量的距离
14.如图所示,有一池塘,要测量两端AB间的距离,可先在平地上取一个在可以直接到达点A和点B的点C,连接AC并延长至点D,使,连结BC并延长至点E,使.连接DE,如果测量出DE=25m,则池塘的宽度是多少呢
解:∵,. ∴.
又∵∠ECD=∠BCA,∴△ECD∽△BCA.
∴.
∵ED =25m,∴AB=255=125(m),
故池塘的宽度是125m.
(三)借助标杆或直尺测量物体的高度
15.如图所示,在高5m的房顶A处观望一幢楼的底部D,视线经过小树的顶端E,又从房底部B处观望楼顶C,视线也正好经过小树的顶端E,测得小树的高度为4m,求楼的高度CD.
解:∵,∴.∵,∴,∴CD = 20m.
核心考点8 位似
16.试画一个四边形,使它和已知四边形ABCD(如图)的位似比等于1:2,位似中心为O.
(1)使两个图形在点O同侧;
(2)使两个图形在点O两侧.
17.如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).
(1)以原点为位似中心在y轴的左侧将△OBC放大到原来的2倍,画除图形.
(2)分别写出B、C两点的对应点B,C的坐标;
(3)如果△OBC内部点M的坐标为(x,y),直接写出M的对应点M的坐标.
解:(1)略
(2)B(-6,2),C(-4,-2),
(3)M(-2x,-2y).
18.在平面直角坐标系系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为言把△EPO缩小,则点E的对应点E的坐标是( D )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
核心考点9 相似与圆
19.如图,△ABC内接于⊙O,BD是⊙O的直径,AC,BD相交于点E, AC=BC,AD=5,DE=2,求⊙O的半径.
解:连接CO并延长交AB于H,∵AC=BC,.∴ CH⊥AB,
∵BD是⊙O的直径,DA⊥AB,∴CH//DA,
∴△COE∽△ADE,∴,
设⊙O的半径为r,则OC=OD=r,OE=r-2,
∴解得.
20.如图,△BCD中,DB=DC,点O在BC上,过B,D两点的⊙O与CD交于点E,若E为CD的中点,求的值.
解:作OH⊥DE于H,作ON⊥BD于N.
设DH=EH=x,则CE=2x,BN=DN=2x,
∵.
核心考点10 相似与二次函数
21.如图,抛物线y=x2-3x-4交x轴交于A,B两点。且过点C(2,m),点G在线段AC上运动(不与A,C重合),若ABG=ACB,求点G的坐标.
解:易求A(-1,0),B(4,0),C(2,-6),可来AC解新式为y=-2x-2,
由△ABG∽△ACB,,AB=5,AC=,,
设G(t,-2t-2),则,,∴
22. 如图,抛物线y=x2-2x-1交y轴于点P,且经过点E(3,2),点F为抛物线上一点,且PFPE,求点F的坐标.
解:分别过E,F作y轴垂线FG,EM,垂足分别为M,G,
∴△MEP∽△GPF,,
又MP=3,ME=3,∴PG=GF,
设F(t,t2-2t-1),GF=t,PG=-1-(t2-2t-1),
t=-1-(t2-2t-1),t1=0(舍去),t2=1,∴F(1,-2).
注:此题还可延长PF交工轴于N,由P,N坐标求PF解析式,后求点F坐标。
核心考点11 相似与反比例函数
23.如图,过原点O的直线与双曲线交于点A,与双曲线交于点B,若OB=2OA,则k的值是 .
解:作AE⊥x轴于E,BF⊥x轴于F.∴△AOE∽△BOF,又OB=2OA,. BF=2AE,FO=2EO,∴k=4.
24.如图,若双曲线与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,且0C=3BD,则k的值是 .
解:过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F,∠AOB=ABO=60°,
设BF=x,则DF=, △COE∽△DBF,
∵OC=3BD,∴OE=3BF=3x,CE=3DF=
∴C(3x,),D(5-x,),
∴,x1=0(舍去),x2=,.
21世纪教育网(www.21cnjy.com)
