32.九年级数学(下)第二十七章 相似专题卷B——核心思想方法归纳一点通(选用)(含答案)
文档属性
| 名称 | 32.九年级数学(下)第二十七章 相似专题卷B——核心思想方法归纳一点通(选用)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 639.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 19:55:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
32.九年级数学(下)第27章《相似》专题卷B——核心思想方法归纳一点通(选用)
一、核心解题方法归纳
核心解题方法1 巧证比例式或等积式
一、三点定型法
【方法技巧】要证明的比例式的四条线段恰好是两个三角形的对应边时,可直接用三点定型法找相似三角形.
1.如图,在等边△ABC中,P为BC上任一点,AP的垂直平分线交AB,AC于M,N两点.求证:BP·PC=BM·CN.
二、等线段代换法
【方法技巧】从要证的结论难以找到相似三角形时,往往可用相等的线段去替换结论中的某些线段,再用三点定型法找相似三角形.
2.如图,在△ABC中,D是BC边上一点,E是AC边上一点,且满足AD=AB,∠ADE=∠C.
求证:AB2=AE·AC.
三、等比代换法(找中间比)
【方法技巧】要证明的比例式无法直接通过平行或相似证出时,往往要找中间比进行过渡.
3.如图,D,E,F分别为△ABC的边上的点,且EF∥AB,交CD于G.求证:=.
四、等积代换(找中间积)
【方法技巧】常借助于射影定理的基本图形和结论找中间积.
4.如图,在△ABC中,AD,BF分别是BC,AC边上的高,过D作AB的垂线交AB于E,交BF于G,交AC的延长线于H.求证:=EG·EH.
核心解题方法2 作平行构造A,X型相似
【方法技巧】同一直线上有公共端点的两条线段的比,常过两线段的三个端点之一作平行线,构造A,X型基本图形解题.
5.如图,在△ABC中,AB>AC,D,E分别在AB,AC上,且AD=AE,DE,BC的延长线交于点P.
(1)若=,求的值.
(2)若=,DE=PE,求的值.
核心解题方法3 作垂线构造直角三角形相似
【方法技巧】作垂线构造两个直角三角形相似.
6.如图,在△ABC中,AB=AC,E,F,G分别是BC,AB,AC上一点,∠FEG=2∠B.
(1)求证:∠BFE=∠AGE;
(2)若=,求的值.
7.如图,P是等边△ABC的边BC上一点,且=,AP的垂直平分线分别交AB,AC于M,N两点,AP和MN交于点Q,求的值.
二、核心数学思想归纳
核心数学思想1 分类讨论思想
8.如图,点P是Rt△ABC的斜边BC上异于B,C的一点.过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )
A.1条 B.2条 C.3条 D.4条
9.在△ABC中,AB=5,AC=9,BC=10,点D为AC上一点,AD=3,在AB上取一点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.
10.如图,在四边形ABCD中,AB∥CD,DA⊥AB,CD=2,AB=3,AD=7,在AD上是否存在点P,使得以点P,A,B为顶点的三角形和以点P,C,D为顶点的三角形相似 若存在,请求出PD的长;若不存在,请说明理由.
核心数学思想2 方程思想
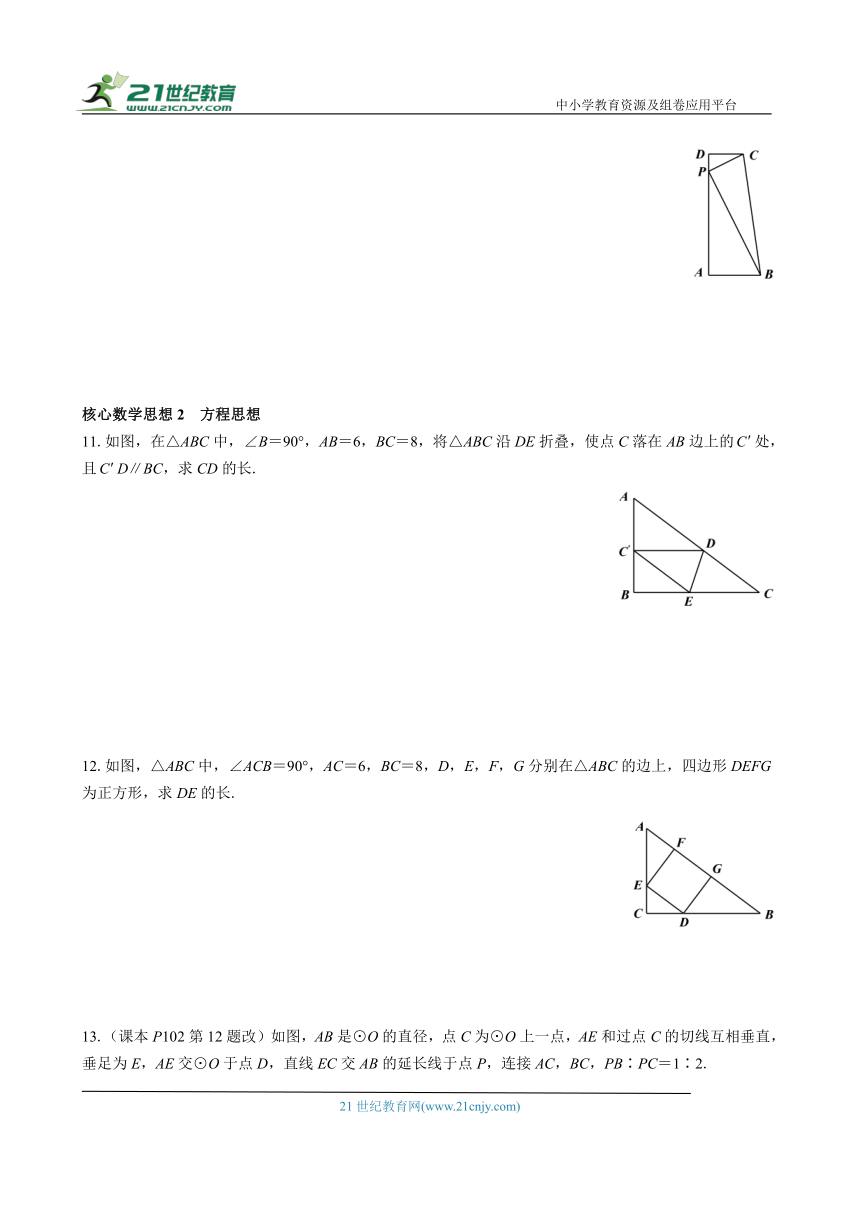
11.如图,在△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边上的处,且D∥BC,求CD的长.
12.如图,△ABC中,∠ACB=90°,AC=6,BC=8,D,E,F,G分别在△ABC的边上,四边形DEFG为正方形,求DE的长.
13.(课本P102第12题改)如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB∶PC=1∶2.
(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求⊙O的半径.
核心数学思想3 转化思想
(一)多边形问题转化为三角形问题
14.如图,已知在四边形ABCD中,AB∥CD,CE平分∠BCD,CE⊥AD于点E,DE=2AE,若△CED的面积为1,求四边形ABCE的面积.
(二)一般问题转化为特殊问题
15.在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F.若AC=mBC,CE=nEA(m,n为实数).试探究线段EF与EG的数量关系.
(1)如图①,当m=1,n=1时,EF与EG的数量关系是 ;
(2)如图②,当m=1,n为任意实数时,探究EF与EG之间的数量关系;
(3)如图③,当m,n为任意实数时,直接写出EF与EG的数量关系是 ;
32.九年级数学(下)第27章《相似》专题卷B——核心思想方法归纳一点通(选用)
一、核心解题方法归纳
核心解题方法1 巧证比例式或等积式
一、三点定型法
【方法技巧】要证明的比例式的四条线段恰好是两个三角形的对应边时,可直接用三点定型法找相似三角形.
1.如图,在等边△ABC中,P为BC上任一点,AP的垂直平分线交AB,AC于M,N两点.求证:BP·PC=BM·CN.
解:证∠MPN=∠BAC=60°,∠BMP=∠NPC,证△PBM∽△NCP即可.
二、等线段代换法
【方法技巧】从要证的结论难以找到相似三角形时,往往可用相等的线段去替换结论中的某些线段,再用三点定型法找相似三角形.
2.如图,在△ABC中,D是BC边上一点,E是AC边上一点,且满足AD=AB,∠ADE=∠C.求证:AB2=AE·AC.
解:证∠AED=∠ADC,可得△AED∽△ADC,得=AE·AC,∵AD=AB,∴=AE·AC.
三、等比代换法(找中间比)
【方法技巧】要证明的比例式无法直接通过平行或相似证出时,往往要找中间比进行过渡.
3.如图,D,E,F分别为△ABC的边上的点,且EF∥AB,交CD于G.求证:=.
解:证=,=,∴=,∴=.
四、等积代换(找中间积)
【方法技巧】常借助于射影定理的基本图形和结论找中间积.
4.如图,在△ABC中,AD,BF分别是BC,AC边上的高,过D作AB的垂线交AB于E,交BF于G,交AC的延长线于H.求证:=EG·EH.
解:先证=BE·AE,再证BE·AE=EG·EH.
核心解题方法2 作平行构造A,X型相似
【方法技巧】同一直线上有公共端点的两条线段的比,常过两线段的三个端点之一作平行线,构造A,X型基本图形解题.
5.如图,在△ABC中,AB>AC,D,E分别在AB,AC上,且AD=AE,DE,BC的延长线交于点P.
(1)若=,求的值.
思路一:作平行线构造“A”型相似
解法一:作CF∥BD交PE于F,∴==,∵AD=AE,AD∥CF,∴CE=CF,∴=.
解法二:过C作CF∥DE交BD于F,易证AF=AC,CE=DF,∴===.
思路二:作平行线构造“X”型相似
解:过B作BF∥PE交EC的延长线于F,易证AB=AF,BD=EF,∴===.
(2)若=,DE=PE,求的值.
思路:作平行线构造“A,X”型
解:过B作BF∥CE交PD的延长线于F,∵AD=AE,∴BF=BD,
∵==,∴==,∵PE=DE,∴==.
核心解题方法3 作垂线构造直角三角形相似
【方法技巧】作垂线构造两个直角三角形相似.
6.如图,在△ABC中,AB=AC,E,F,G分别是BC,AB,AC上一点,∠FEG=2∠B.
(1)求证:∠BFE=∠AGE;
(2)若=,求的值.
解:(1)∵2∠B+∠A=180°,∴∠FEG+∠A=180°,∴∠BFE=∠AGE;
(2)过E作EM⊥AB于M,作EN⊥AC于N,∴△EMF∽△ENG,∴=,
易证△EBM∽△ECN,∴==,∴=.
7.如图,P是等边△ABC的边BC上一点,且=,AP的垂直平分线分别交AB,AC于M,N两点,AP和MN交于点Q,求的值.
解:过点P分别向AB、AC作垂线PE、PF,E、F为垂足,
可得△AMQ∽△APE和△ANQ∽△APF,
∴=①,=②,由①÷②可得=,
由=可设BP=2,CP=3,
∴AB=AC=5,Rt△BPE中BE=BP=1,∴AE=4,
Rt△PCF中,CF=CP=,∴AF=,∴==.
二、核心数学思想归纳
核心数学思想1 分类讨论思想
8.如图,点P是Rt△ABC的斜边BC上异于B,C的一点.过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( C )
A.1条 B.2条 C.3条 D.4条
9.在△ABC中,AB=5,AC=9,BC=10,点D为AC上一点,AD=3,在AB上取一点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.
解:①当△ADE∽△ABC时,由=,可得DE=6;
②当△ADE∽△ACB时,由=可得DE=.
10.如图,在四边形ABCD中,AB∥CD,DA⊥AB,CD=2,AB=3,AD=7,在AD上是否存在点P,使得以点P,A,B为顶点的三角形和以点P,C,D为顶点的三角形相似 若存在,请求出PD的长;若不存在,请说明理由.
解:假设存在符合題意的点P,有如下两种情况:设PD=x,则AP=7-x.
①若△PDC∽△PAB,则=,∵CD=2,AB=3,∴=,解得x=.
②若△PDC∽△BAP,则=,∴=,即-7x+6=0.解得x=1或6.
当x=或1或6时,均符合题意.
综上:PD长为或1或6.
核心数学思想2 方程思想
11.如图,在△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边上的处,且D∥BC,求CD的长.
解:AC=10,设CD=D=x,AD=10-x,∵=,∴=,x=,∴CD=.
12.如图,△ABC中,∠ACB=90°,AC=6,BC=8,D,E,F,G分别在△ABC的边上,四边形DEFG为正方形,求DE的长.
解:作CM⊥AB于M,交DE于N,∵AC·BC=AB·CM,∴CM=,设DE=x,
∵=,∴=,∴x=,∴DE的长为.
13.(课本P102第12题改)如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB∶PC=1∶2.
(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求⊙O的半径.
解:(1)连接OC,则OC∥AE,证∠EAC=∠OCA=∠OAC.
(2)证△PBC∽△PCA,∴=PB·PA,∴4PB2=PB·PA,∴PA=4PB,∴AB=3PB.
(3)作OH⊥AD于H,则AH=DH=,四边形OHEC为矩形,
设⊙O的半径为R,则HE=OC=R,∴AE=+R,
∵△POC∽△PAE,∴=,∵AB=3PB,∴PB=R,∴=,∴R=.
核心数学思想3 转化思想
(一)多边形问题转化为三角形问题
14.如图,已知在四边形ABCD中,AB∥CD,CE平分∠BCD,CE⊥AD于点E,DE=2AE,若△CED的面积为1,求四边形ABCE的面积.
解:如图,分别延长CB、DA交于点F.又∵CE平分∠BCD,CE⊥AD,
∴△FCD为等腰三角形,E为FD的中点,∴=FD·CE=×2ED·CE=2=2.
∵DE=2AE,DE=EF,∴EF=2AE,∴FA=AE=FD.
又∵AB∥CD,∴△FBA∽△FCD,===,
∴==,∴=--=2-1-=.
(二)一般问题转化为特殊问题
15.在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F.若AC=mBC,CE=nEA(m,n为实数).试探究线段EF与EG的数量关系.
(1)如图①,当m=1,n=1时,EF与EG的数量关系是 ;
(2)如图②,当m=1,n为任意实数时,探究EF与EG之间的数量关系;
(3)如图③,当m,n为任意实数时,直接写出EF与EG的数量关系是 ;
解:(1)EF=EG,证明△FEA≌△GED;
(2)EG=nEF,证明:过E作EP⊥CD于P,EQ⊥AB于Q,
证明△CEP∽△AEQ,∴==n,
∵∠FEG=∠GEP=90°,∴∠FEQ=∠GEP,
又∠EQF=∠EPG=90°,∴△FEQ∽△GEP,∴==n,∴EG=nEF;
(3)EG=mnEF.
提示:证==n,∴CP=n·EQ,
证==m,∴EP=m·CP=mn·EQ,
证===mn.
21世纪教育网(www.21cnjy.com)
32.九年级数学(下)第27章《相似》专题卷B——核心思想方法归纳一点通(选用)
一、核心解题方法归纳
核心解题方法1 巧证比例式或等积式
一、三点定型法
【方法技巧】要证明的比例式的四条线段恰好是两个三角形的对应边时,可直接用三点定型法找相似三角形.
1.如图,在等边△ABC中,P为BC上任一点,AP的垂直平分线交AB,AC于M,N两点.求证:BP·PC=BM·CN.
二、等线段代换法
【方法技巧】从要证的结论难以找到相似三角形时,往往可用相等的线段去替换结论中的某些线段,再用三点定型法找相似三角形.
2.如图,在△ABC中,D是BC边上一点,E是AC边上一点,且满足AD=AB,∠ADE=∠C.
求证:AB2=AE·AC.
三、等比代换法(找中间比)
【方法技巧】要证明的比例式无法直接通过平行或相似证出时,往往要找中间比进行过渡.
3.如图,D,E,F分别为△ABC的边上的点,且EF∥AB,交CD于G.求证:=.
四、等积代换(找中间积)
【方法技巧】常借助于射影定理的基本图形和结论找中间积.
4.如图,在△ABC中,AD,BF分别是BC,AC边上的高,过D作AB的垂线交AB于E,交BF于G,交AC的延长线于H.求证:=EG·EH.
核心解题方法2 作平行构造A,X型相似
【方法技巧】同一直线上有公共端点的两条线段的比,常过两线段的三个端点之一作平行线,构造A,X型基本图形解题.
5.如图,在△ABC中,AB>AC,D,E分别在AB,AC上,且AD=AE,DE,BC的延长线交于点P.
(1)若=,求的值.
(2)若=,DE=PE,求的值.
核心解题方法3 作垂线构造直角三角形相似
【方法技巧】作垂线构造两个直角三角形相似.
6.如图,在△ABC中,AB=AC,E,F,G分别是BC,AB,AC上一点,∠FEG=2∠B.
(1)求证:∠BFE=∠AGE;
(2)若=,求的值.
7.如图,P是等边△ABC的边BC上一点,且=,AP的垂直平分线分别交AB,AC于M,N两点,AP和MN交于点Q,求的值.
二、核心数学思想归纳
核心数学思想1 分类讨论思想
8.如图,点P是Rt△ABC的斜边BC上异于B,C的一点.过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )
A.1条 B.2条 C.3条 D.4条
9.在△ABC中,AB=5,AC=9,BC=10,点D为AC上一点,AD=3,在AB上取一点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.
10.如图,在四边形ABCD中,AB∥CD,DA⊥AB,CD=2,AB=3,AD=7,在AD上是否存在点P,使得以点P,A,B为顶点的三角形和以点P,C,D为顶点的三角形相似 若存在,请求出PD的长;若不存在,请说明理由.
核心数学思想2 方程思想
11.如图,在△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边上的处,且D∥BC,求CD的长.
12.如图,△ABC中,∠ACB=90°,AC=6,BC=8,D,E,F,G分别在△ABC的边上,四边形DEFG为正方形,求DE的长.
13.(课本P102第12题改)如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB∶PC=1∶2.
(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求⊙O的半径.
核心数学思想3 转化思想
(一)多边形问题转化为三角形问题
14.如图,已知在四边形ABCD中,AB∥CD,CE平分∠BCD,CE⊥AD于点E,DE=2AE,若△CED的面积为1,求四边形ABCE的面积.
(二)一般问题转化为特殊问题
15.在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F.若AC=mBC,CE=nEA(m,n为实数).试探究线段EF与EG的数量关系.
(1)如图①,当m=1,n=1时,EF与EG的数量关系是 ;
(2)如图②,当m=1,n为任意实数时,探究EF与EG之间的数量关系;
(3)如图③,当m,n为任意实数时,直接写出EF与EG的数量关系是 ;
32.九年级数学(下)第27章《相似》专题卷B——核心思想方法归纳一点通(选用)
一、核心解题方法归纳
核心解题方法1 巧证比例式或等积式
一、三点定型法
【方法技巧】要证明的比例式的四条线段恰好是两个三角形的对应边时,可直接用三点定型法找相似三角形.
1.如图,在等边△ABC中,P为BC上任一点,AP的垂直平分线交AB,AC于M,N两点.求证:BP·PC=BM·CN.
解:证∠MPN=∠BAC=60°,∠BMP=∠NPC,证△PBM∽△NCP即可.
二、等线段代换法
【方法技巧】从要证的结论难以找到相似三角形时,往往可用相等的线段去替换结论中的某些线段,再用三点定型法找相似三角形.
2.如图,在△ABC中,D是BC边上一点,E是AC边上一点,且满足AD=AB,∠ADE=∠C.求证:AB2=AE·AC.
解:证∠AED=∠ADC,可得△AED∽△ADC,得=AE·AC,∵AD=AB,∴=AE·AC.
三、等比代换法(找中间比)
【方法技巧】要证明的比例式无法直接通过平行或相似证出时,往往要找中间比进行过渡.
3.如图,D,E,F分别为△ABC的边上的点,且EF∥AB,交CD于G.求证:=.
解:证=,=,∴=,∴=.
四、等积代换(找中间积)
【方法技巧】常借助于射影定理的基本图形和结论找中间积.
4.如图,在△ABC中,AD,BF分别是BC,AC边上的高,过D作AB的垂线交AB于E,交BF于G,交AC的延长线于H.求证:=EG·EH.
解:先证=BE·AE,再证BE·AE=EG·EH.
核心解题方法2 作平行构造A,X型相似
【方法技巧】同一直线上有公共端点的两条线段的比,常过两线段的三个端点之一作平行线,构造A,X型基本图形解题.
5.如图,在△ABC中,AB>AC,D,E分别在AB,AC上,且AD=AE,DE,BC的延长线交于点P.
(1)若=,求的值.
思路一:作平行线构造“A”型相似
解法一:作CF∥BD交PE于F,∴==,∵AD=AE,AD∥CF,∴CE=CF,∴=.
解法二:过C作CF∥DE交BD于F,易证AF=AC,CE=DF,∴===.
思路二:作平行线构造“X”型相似
解:过B作BF∥PE交EC的延长线于F,易证AB=AF,BD=EF,∴===.
(2)若=,DE=PE,求的值.
思路:作平行线构造“A,X”型
解:过B作BF∥CE交PD的延长线于F,∵AD=AE,∴BF=BD,
∵==,∴==,∵PE=DE,∴==.
核心解题方法3 作垂线构造直角三角形相似
【方法技巧】作垂线构造两个直角三角形相似.
6.如图,在△ABC中,AB=AC,E,F,G分别是BC,AB,AC上一点,∠FEG=2∠B.
(1)求证:∠BFE=∠AGE;
(2)若=,求的值.
解:(1)∵2∠B+∠A=180°,∴∠FEG+∠A=180°,∴∠BFE=∠AGE;
(2)过E作EM⊥AB于M,作EN⊥AC于N,∴△EMF∽△ENG,∴=,
易证△EBM∽△ECN,∴==,∴=.
7.如图,P是等边△ABC的边BC上一点,且=,AP的垂直平分线分别交AB,AC于M,N两点,AP和MN交于点Q,求的值.
解:过点P分别向AB、AC作垂线PE、PF,E、F为垂足,
可得△AMQ∽△APE和△ANQ∽△APF,
∴=①,=②,由①÷②可得=,
由=可设BP=2,CP=3,
∴AB=AC=5,Rt△BPE中BE=BP=1,∴AE=4,
Rt△PCF中,CF=CP=,∴AF=,∴==.
二、核心数学思想归纳
核心数学思想1 分类讨论思想
8.如图,点P是Rt△ABC的斜边BC上异于B,C的一点.过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( C )
A.1条 B.2条 C.3条 D.4条
9.在△ABC中,AB=5,AC=9,BC=10,点D为AC上一点,AD=3,在AB上取一点E,使以A,D,E为顶点的三角形与△ABC相似,求DE的长.
解:①当△ADE∽△ABC时,由=,可得DE=6;
②当△ADE∽△ACB时,由=可得DE=.
10.如图,在四边形ABCD中,AB∥CD,DA⊥AB,CD=2,AB=3,AD=7,在AD上是否存在点P,使得以点P,A,B为顶点的三角形和以点P,C,D为顶点的三角形相似 若存在,请求出PD的长;若不存在,请说明理由.
解:假设存在符合題意的点P,有如下两种情况:设PD=x,则AP=7-x.
①若△PDC∽△PAB,则=,∵CD=2,AB=3,∴=,解得x=.
②若△PDC∽△BAP,则=,∴=,即-7x+6=0.解得x=1或6.
当x=或1或6时,均符合题意.
综上:PD长为或1或6.
核心数学思想2 方程思想
11.如图,在△ABC中,∠B=90°,AB=6,BC=8,将△ABC沿DE折叠,使点C落在AB边上的处,且D∥BC,求CD的长.
解:AC=10,设CD=D=x,AD=10-x,∵=,∴=,x=,∴CD=.
12.如图,△ABC中,∠ACB=90°,AC=6,BC=8,D,E,F,G分别在△ABC的边上,四边形DEFG为正方形,求DE的长.
解:作CM⊥AB于M,交DE于N,∵AC·BC=AB·CM,∴CM=,设DE=x,
∵=,∴=,∴x=,∴DE的长为.
13.(课本P102第12题改)如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB∶PC=1∶2.
(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求⊙O的半径.
解:(1)连接OC,则OC∥AE,证∠EAC=∠OCA=∠OAC.
(2)证△PBC∽△PCA,∴=PB·PA,∴4PB2=PB·PA,∴PA=4PB,∴AB=3PB.
(3)作OH⊥AD于H,则AH=DH=,四边形OHEC为矩形,
设⊙O的半径为R,则HE=OC=R,∴AE=+R,
∵△POC∽△PAE,∴=,∵AB=3PB,∴PB=R,∴=,∴R=.
核心数学思想3 转化思想
(一)多边形问题转化为三角形问题
14.如图,已知在四边形ABCD中,AB∥CD,CE平分∠BCD,CE⊥AD于点E,DE=2AE,若△CED的面积为1,求四边形ABCE的面积.
解:如图,分别延长CB、DA交于点F.又∵CE平分∠BCD,CE⊥AD,
∴△FCD为等腰三角形,E为FD的中点,∴=FD·CE=×2ED·CE=2=2.
∵DE=2AE,DE=EF,∴EF=2AE,∴FA=AE=FD.
又∵AB∥CD,∴△FBA∽△FCD,===,
∴==,∴=--=2-1-=.
(二)一般问题转化为特殊问题
15.在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F.若AC=mBC,CE=nEA(m,n为实数).试探究线段EF与EG的数量关系.
(1)如图①,当m=1,n=1时,EF与EG的数量关系是 ;
(2)如图②,当m=1,n为任意实数时,探究EF与EG之间的数量关系;
(3)如图③,当m,n为任意实数时,直接写出EF与EG的数量关系是 ;
解:(1)EF=EG,证明△FEA≌△GED;
(2)EG=nEF,证明:过E作EP⊥CD于P,EQ⊥AB于Q,
证明△CEP∽△AEQ,∴==n,
∵∠FEG=∠GEP=90°,∴∠FEQ=∠GEP,
又∠EQF=∠EPG=90°,∴△FEQ∽△GEP,∴==n,∴EG=nEF;
(3)EG=mnEF.
提示:证==n,∴CP=n·EQ,
证==m,∴EP=m·CP=mn·EQ,
证===mn.
21世纪教育网(www.21cnjy.com)
