33.九年级数学(下)第二十七章 相似单元检测题(含答案)
文档属性
| 名称 | 33.九年级数学(下)第二十七章 相似单元检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 470.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 19:46:31 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
33.九年级数学(下)第27章《相似》单元检测题
(考试范围:全章综合测试 解答参考时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.(教材变式·9下P25习题1改)将等边三角形的三边各扩大2倍后得到的三角形是( )
A.等边三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
2.在△ABC和△A′B′C′中,∠A=62°,∠B=50°,∠A′=62°,∠C′=68°,那么这两个三角形( )
A.相似 B.全等 C.不相似 D.无法确定
3.如图,△ABC中,DE∥BC,AD=3,BD=6,AE=2,则CE的长为( )
A.9 B.6 C.3 D.4
第3题图 第4题图 第5题图
4.如图,将△AOB以O为位似中心,扩大到△COD,各点坐标分别为A(1,2),B(3,0),D(6,0),则点C的坐标为( )
A.(2,3) B.(2,4) C.(3,3) D.(3,4)
5.图中的两个三角形是位似图形,则它们的位似中心是( )
A.点P B.点Q C.点R D.点S
6.如图,点D在△ABC的边AC上,要使△ADB与△ABC相似,添加一个条件,错误的是( )
A.∠ABD=∠C B.∠ADB=∠ABC
C. D.
7.如图,□ABCD中,点N是AB上一点,且BN=2AN,AC、DN相交于点M,则AM:MC的值是( )
A.1:4 B.1:3 C.1:9 D.3:10
第7题图 第8题图 第9题图
8.△ABC中,∠ACB=90°,将△ABC按如图的位置放在直角坐标系中,若点A的坐标为(0,2),点C的坐标为(1,0),点B的横坐标为4,则点B的纵坐标为( )
A.1 B.1.5 C.1.2 D.1.8
9.如图,△ABC中,∠C=90°,以AB上一点O为圆心作⊙O,分别切AC、BC于E、D,AC=8,BC=6,则⊙O的半径长为( )
A. 5 B. C. D.
10.如图,在△ABC中,AB=8,AC=6,若D在AC上,且AD=2,若要在AB上找一点E,要使△ADE与△ABC相似,则AE的长为( )
A. B. C. D.
二、填空题(每小题3分,共18分)
11.如图,请你补充一个条件,使△ABC∽△ACD,这个条件是 .
第10题图 第13题图 第14题图
12.△ABC与△DEF的相似比为2:5,则△ABC与△DEF的面积比为 .
13.在□ABCD中,E在DC上,若DE:EC=2:3,则△CEF与△ABF的周长比为 .
14.(教材变式·9下P42习题5改)如图,△ABC中,DE∥FG∥BC,AD:DF:FB=1:2:3,若EG=4,则AC= .
15.如图,在平面直角坐标系中,△OBA∽△DOC,边OA、OC都在x轴的正半轴上,已知B(6,8),∠BAO=∠OCD=90°,OD=5,双曲线经过点D,则k的值是 .
16.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,DE⊥AP交AP于E,若∠APD=60°,则 .
三、解答题(共8小题,共72分)
17.(本题8分)如图,点D、E在BC上,且FD∥AB,FE∥AC,若BD+CE=DE,求的值
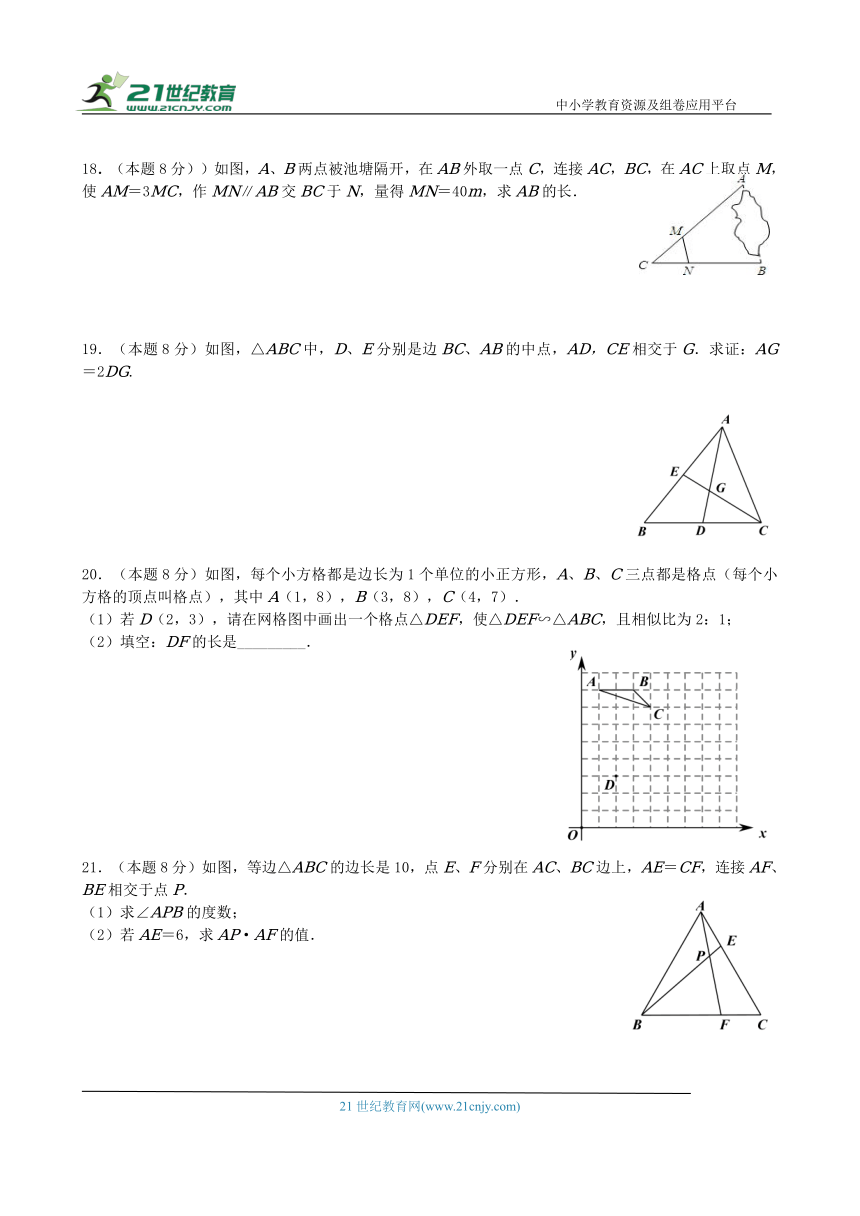
18.(本题8分))如图,A、B两点被池塘隔开,在AB外取一点C,连接AC,BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于N,量得MN=40m,求AB的长.
19.(本题8分)如图,△ABC中,D、E分别是边BC、AB的中点,AD,CE相交于G.求证:AG=2DG.
20.(本题8分)如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
(1)若D(2,3),请在网格图中画出一个格点△DEF,使△DEF∽△ABC,且相似比为2:1;
(2)填空:DF的长是_________.
21.(本题8分)如图,等边△ABC的边长是10,点E、F分别在AC、BC边上,AE=CF,连接AF、BE相交于点P.
(1)求∠APB的度数;
(2)若AE=6,求AP·AF的值.
22.(本题10分)如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO.并延长AO交⊙0于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若求 的值
23.(本题10分)如图,矩形ABCD中,AB=6,AD=8,动点P从点D出发,以每秒5个单位的速度向点B匀速运动,同时动点Q从点A出发,以每秒4个单位的速度向点D匀速运动,运动的时间为t秒(0<t<2).
(1)如图1,连接CQ,当t为何值时CQ=BC;
(2)如图2,连接AP、BQ,若BQ⊥AP,求t的值.
24.(本题12分)如图1,过原点的抛物线y=-x2+b x的对称轴为x=2,直线y=kx+4与y轴,抛物线依次交于点D,E,F.
(1)求抛物线的解析式;
(2)若求k的值
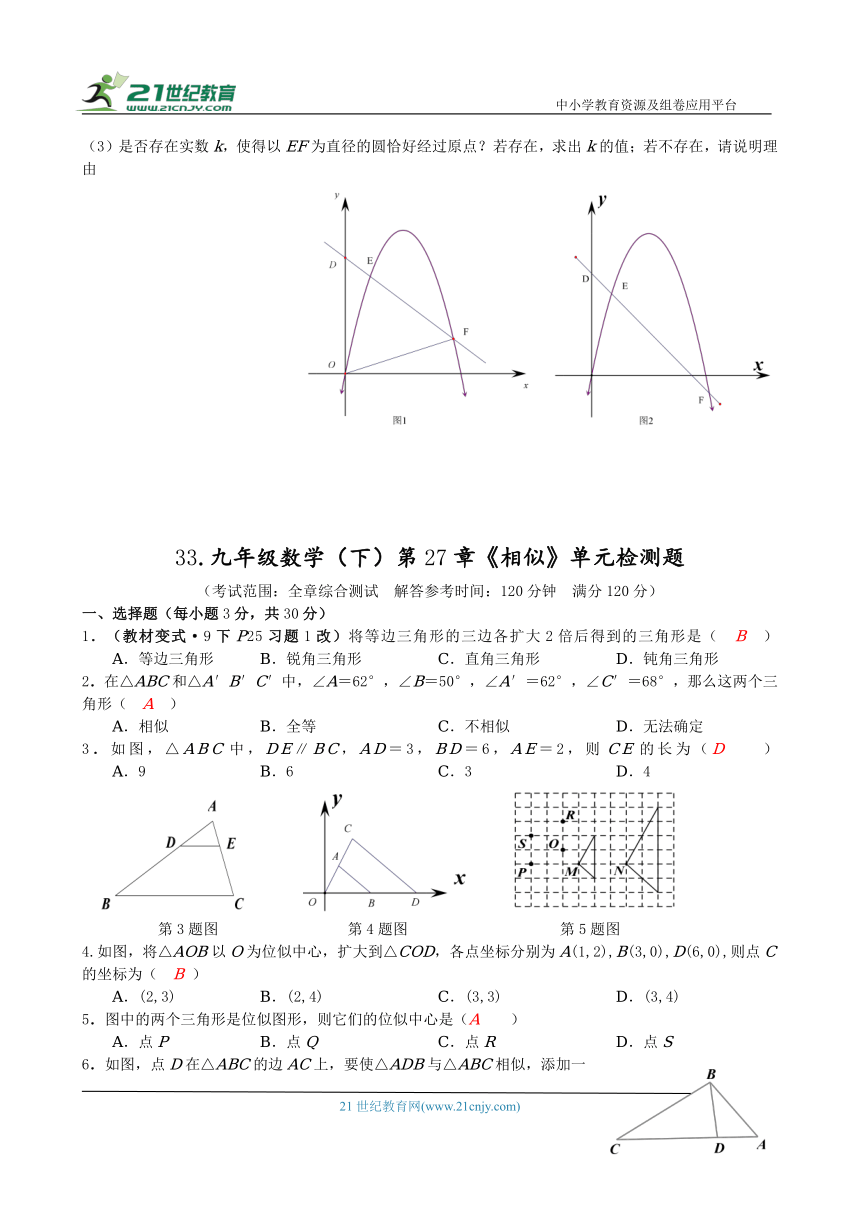
(3)是否存在实数k,使得以EF为直径的圆恰好经过原点?若存在,求出k的值;若不存在,请说明理由
33.九年级数学(下)第27章《相似》单元检测题
(考试范围:全章综合测试 解答参考时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.(教材变式·9下P25习题1改)将等边三角形的三边各扩大2倍后得到的三角形是( B )
A.等边三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
2.在△ABC和△A′B′C′中,∠A=62°,∠B=50°,∠A′=62°,∠C′=68°,那么这两个三角形( A )
A.相似 B.全等 C.不相似 D.无法确定
3.如图,△ABC中,DE∥BC,AD=3,BD=6,AE=2,则CE的长为(D )
A.9 B.6 C.3 D.4
第3题图 第4题图 第5题图
4.如图,将△AOB以O为位似中心,扩大到△COD,各点坐标分别为A(1,2),B(3,0),D(6,0),则点C的坐标为( B )
A.(2,3) B.(2,4) C.(3,3) D.(3,4)
5.图中的两个三角形是位似图形,则它们的位似中心是(A )
A.点P B.点Q C.点R D.点S
6.如图,点D在△ABC的边AC上,要使△ADB与△ABC相似,添加一个条件,错误的是( C)
A.∠ABD=∠C B.∠ADB=∠ABC
C. D.
7.如图,□ABCD中,点N是AB上一点,且BN=2AN,AC、DN相交于点M,则AM:MC的值是( A )
A.1:4 B.1:3 C.1:9 D.3:10
第7题图 第8题图 第9题图
8.△ABC中,∠ACB=90°,将△ABC按如图的位置放在直角坐标系中,若点A的坐标为(0,2),点C的坐标为(1,0),点B的横坐标为4,则点B的纵坐标为( B )
A.1 B.1.5 C.1.2 D.1.8
9.如图,△ABC中,∠C=90°,以AB上一点O为圆心作⊙O,分别切AC、BC于E、D,AC=8,BC=6,则⊙O的半径长为( D )
A. 5 B. C. D.
10.如图,在△ABC中,AB=8,AC=6,若D在AC上,且AD=2,若要在AB上找一点E,要使△ADE与△ABC相似,则AE的长为(D)
A. B. C. D.
二、填空题(每小题3分,共18分)
11.如图,请你补充一个条件,使△ABC∽△ACD,这个条件是∠ACD=∠B.
第10题图 第13题图 第14题图
12.△ABC与△DEF的相似比为2:5,则△ABC与△DEF的面积比为 4:25 .
13.在□ABCD中,E在DC上,若DE:EC=2:3,则△CEF与△ABF的周长比为 3:5 .
14.(教材变式·9下P42习题5改)如图,△ABC中,DE∥FG∥BC,AD:DF:FB=1:2:3,若EG=4,则AC=12.
15.如图,在平面直角坐标系中,△OBA∽△DOC,边OA、OC都在x轴的正半轴上,已知B(6,8),∠BAO=∠OCD=90°,OD=5,双曲线经过点D,则k的值是 12 .
16.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,DE⊥AP交AP于E,若∠APD=60°,则.
三、解答题(共8小题,共72分)
17.(本题8分)如图,点D、E在BC上,且FD∥AB,FE∥AC,
若BD+CE=DE,求的值
解:∵ FD∥AB,∴∠B =∠FDE, 由∵EF∥AC,∴∠C =∠FEDE,
∴△ABC∽△FDE,∴
18.(本题8分))如图,A、B两点被池塘隔开,在AB外取一点C,连接AC,BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于N,量得MN=40m,求AB的长.
解:AB=160m
19.(本题8分)如图,△ABC中,D、E分别是边BC、AB的中点,AD,CE相交于G.求证:AG=2DG.
解:连ED,则ED∥AC,且ED=证△DEG∽△ACG,
∴
20.(本题8分)如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
(1)若D(2,3),请在网格图中画出一个格点△DEF,使△DEF∽△ABC,且相似比为2:1;
(2)填空:DF的长是_________.
解:(1)略;
(2)DF=
21.(本题8分)如图,等边△ABC的边长是10,点E、F分别在AC、BC边上,AE=CF,连接AF、BE相交于点P.
(1)求∠APB的度数;
(2)若AE=6,求AP·AF的值.
解:(1)易证△ABE∽△CAF, 易求∠APB=120°
(2)证△APE∽△ACF,∴AP·AF=AE·AC=4×10=40.
22.(本题10分)如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO.并延长AO交⊙0于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若求 的值
解:(1)证OP垂直平分AB,△PAO≌△PBD即可
(2)∵ 故设OC=2x,AC=3x,由 得PC=
∴PO=PC+OC=易证∠ABE=90°,OC∥BE,
∴BE=2CO=4x,∴∴.
23.(本题10分)如图,矩形ABCD中,AB=6,AD=8,动点P从点D出发,以每秒5个单位的速度向点B匀速运动,同时动点Q从点A出发,以每秒4个单位的速度向点D匀速运动,运动的时间为t秒(0<t<2).
(1)如图1,连接CQ,当t为何值时CQ=BC;
(2)如图2,连接AP、BQ,若BQ⊥AP,求t的值.
解:(1)∵AQ=4t,AD=8,∴DQ=8-4t,
又∵AB=6,∴由勾股定理得,
∵CQ=BC,解得t=2-
(2)过P作PE⊥AD于E,∴AB∥PE,∴△DEP∽△DAB,∴
∴
∵∠ABQ+∠BAP=90°, ∠EAP+∠BAP=90°,∴∠ABQ=∠EAP∵∠AEP=∠BAQ,
∴△BAQ∽△AEP,∴即
24.(本题12分)如图1,过原点的抛物线y=-x2+b x的对称轴为x=2,直线y=kx+4与y轴,抛物线依次交于点D,E,F.
(1)求抛物线的解析式;
(2)若求k的值
(3)是否存在实数k,使得以EF为直径的圆恰好经过原点?若存在,求出k的值;若不存在,请说明理由
解:(1)y=-x2十4x
(2)过E作EM⊥OD于M,过F作FN⊥EM于N,由
得-x2+(4-k)x-4=0, +=4-k①,·=4②,
可得△DEM∽△FEN,=4,③由①②③即xE>0,
得=1,=4,+=5=4-k,k=-1;
3)作EP⊥OD于P,作FQ⊥y轴于Q、可得∠EOF=90°,∠PEO=∠QOF,
∵△OPE∽△FQO,∴∴-+4=
-·+4(+)-16=1 得=4,+=4-k,代入上式得,
-4+16-4k-16=1,k
第16题图
第15题图
图2
图1
第16题图
第15题图
图2
图1
21世纪教育网(www.21cnjy.com)
33.九年级数学(下)第27章《相似》单元检测题
(考试范围:全章综合测试 解答参考时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.(教材变式·9下P25习题1改)将等边三角形的三边各扩大2倍后得到的三角形是( )
A.等边三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
2.在△ABC和△A′B′C′中,∠A=62°,∠B=50°,∠A′=62°,∠C′=68°,那么这两个三角形( )
A.相似 B.全等 C.不相似 D.无法确定
3.如图,△ABC中,DE∥BC,AD=3,BD=6,AE=2,则CE的长为( )
A.9 B.6 C.3 D.4
第3题图 第4题图 第5题图
4.如图,将△AOB以O为位似中心,扩大到△COD,各点坐标分别为A(1,2),B(3,0),D(6,0),则点C的坐标为( )
A.(2,3) B.(2,4) C.(3,3) D.(3,4)
5.图中的两个三角形是位似图形,则它们的位似中心是( )
A.点P B.点Q C.点R D.点S
6.如图,点D在△ABC的边AC上,要使△ADB与△ABC相似,添加一个条件,错误的是( )
A.∠ABD=∠C B.∠ADB=∠ABC
C. D.
7.如图,□ABCD中,点N是AB上一点,且BN=2AN,AC、DN相交于点M,则AM:MC的值是( )
A.1:4 B.1:3 C.1:9 D.3:10
第7题图 第8题图 第9题图
8.△ABC中,∠ACB=90°,将△ABC按如图的位置放在直角坐标系中,若点A的坐标为(0,2),点C的坐标为(1,0),点B的横坐标为4,则点B的纵坐标为( )
A.1 B.1.5 C.1.2 D.1.8
9.如图,△ABC中,∠C=90°,以AB上一点O为圆心作⊙O,分别切AC、BC于E、D,AC=8,BC=6,则⊙O的半径长为( )
A. 5 B. C. D.
10.如图,在△ABC中,AB=8,AC=6,若D在AC上,且AD=2,若要在AB上找一点E,要使△ADE与△ABC相似,则AE的长为( )
A. B. C. D.
二、填空题(每小题3分,共18分)
11.如图,请你补充一个条件,使△ABC∽△ACD,这个条件是 .
第10题图 第13题图 第14题图
12.△ABC与△DEF的相似比为2:5,则△ABC与△DEF的面积比为 .
13.在□ABCD中,E在DC上,若DE:EC=2:3,则△CEF与△ABF的周长比为 .
14.(教材变式·9下P42习题5改)如图,△ABC中,DE∥FG∥BC,AD:DF:FB=1:2:3,若EG=4,则AC= .
15.如图,在平面直角坐标系中,△OBA∽△DOC,边OA、OC都在x轴的正半轴上,已知B(6,8),∠BAO=∠OCD=90°,OD=5,双曲线经过点D,则k的值是 .
16.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,DE⊥AP交AP于E,若∠APD=60°,则 .
三、解答题(共8小题,共72分)
17.(本题8分)如图,点D、E在BC上,且FD∥AB,FE∥AC,若BD+CE=DE,求的值
18.(本题8分))如图,A、B两点被池塘隔开,在AB外取一点C,连接AC,BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于N,量得MN=40m,求AB的长.
19.(本题8分)如图,△ABC中,D、E分别是边BC、AB的中点,AD,CE相交于G.求证:AG=2DG.
20.(本题8分)如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
(1)若D(2,3),请在网格图中画出一个格点△DEF,使△DEF∽△ABC,且相似比为2:1;
(2)填空:DF的长是_________.
21.(本题8分)如图,等边△ABC的边长是10,点E、F分别在AC、BC边上,AE=CF,连接AF、BE相交于点P.
(1)求∠APB的度数;
(2)若AE=6,求AP·AF的值.
22.(本题10分)如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO.并延长AO交⊙0于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若求 的值
23.(本题10分)如图,矩形ABCD中,AB=6,AD=8,动点P从点D出发,以每秒5个单位的速度向点B匀速运动,同时动点Q从点A出发,以每秒4个单位的速度向点D匀速运动,运动的时间为t秒(0<t<2).
(1)如图1,连接CQ,当t为何值时CQ=BC;
(2)如图2,连接AP、BQ,若BQ⊥AP,求t的值.
24.(本题12分)如图1,过原点的抛物线y=-x2+b x的对称轴为x=2,直线y=kx+4与y轴,抛物线依次交于点D,E,F.
(1)求抛物线的解析式;
(2)若求k的值
(3)是否存在实数k,使得以EF为直径的圆恰好经过原点?若存在,求出k的值;若不存在,请说明理由
33.九年级数学(下)第27章《相似》单元检测题
(考试范围:全章综合测试 解答参考时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.(教材变式·9下P25习题1改)将等边三角形的三边各扩大2倍后得到的三角形是( B )
A.等边三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
2.在△ABC和△A′B′C′中,∠A=62°,∠B=50°,∠A′=62°,∠C′=68°,那么这两个三角形( A )
A.相似 B.全等 C.不相似 D.无法确定
3.如图,△ABC中,DE∥BC,AD=3,BD=6,AE=2,则CE的长为(D )
A.9 B.6 C.3 D.4
第3题图 第4题图 第5题图
4.如图,将△AOB以O为位似中心,扩大到△COD,各点坐标分别为A(1,2),B(3,0),D(6,0),则点C的坐标为( B )
A.(2,3) B.(2,4) C.(3,3) D.(3,4)
5.图中的两个三角形是位似图形,则它们的位似中心是(A )
A.点P B.点Q C.点R D.点S
6.如图,点D在△ABC的边AC上,要使△ADB与△ABC相似,添加一个条件,错误的是( C)
A.∠ABD=∠C B.∠ADB=∠ABC
C. D.
7.如图,□ABCD中,点N是AB上一点,且BN=2AN,AC、DN相交于点M,则AM:MC的值是( A )
A.1:4 B.1:3 C.1:9 D.3:10
第7题图 第8题图 第9题图
8.△ABC中,∠ACB=90°,将△ABC按如图的位置放在直角坐标系中,若点A的坐标为(0,2),点C的坐标为(1,0),点B的横坐标为4,则点B的纵坐标为( B )
A.1 B.1.5 C.1.2 D.1.8
9.如图,△ABC中,∠C=90°,以AB上一点O为圆心作⊙O,分别切AC、BC于E、D,AC=8,BC=6,则⊙O的半径长为( D )
A. 5 B. C. D.
10.如图,在△ABC中,AB=8,AC=6,若D在AC上,且AD=2,若要在AB上找一点E,要使△ADE与△ABC相似,则AE的长为(D)
A. B. C. D.
二、填空题(每小题3分,共18分)
11.如图,请你补充一个条件,使△ABC∽△ACD,这个条件是∠ACD=∠B.
第10题图 第13题图 第14题图
12.△ABC与△DEF的相似比为2:5,则△ABC与△DEF的面积比为 4:25 .
13.在□ABCD中,E在DC上,若DE:EC=2:3,则△CEF与△ABF的周长比为 3:5 .
14.(教材变式·9下P42习题5改)如图,△ABC中,DE∥FG∥BC,AD:DF:FB=1:2:3,若EG=4,则AC=12.
15.如图,在平面直角坐标系中,△OBA∽△DOC,边OA、OC都在x轴的正半轴上,已知B(6,8),∠BAO=∠OCD=90°,OD=5,双曲线经过点D,则k的值是 12 .
16.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,DE⊥AP交AP于E,若∠APD=60°,则.
三、解答题(共8小题,共72分)
17.(本题8分)如图,点D、E在BC上,且FD∥AB,FE∥AC,
若BD+CE=DE,求的值
解:∵ FD∥AB,∴∠B =∠FDE, 由∵EF∥AC,∴∠C =∠FEDE,
∴△ABC∽△FDE,∴
18.(本题8分))如图,A、B两点被池塘隔开,在AB外取一点C,连接AC,BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于N,量得MN=40m,求AB的长.
解:AB=160m
19.(本题8分)如图,△ABC中,D、E分别是边BC、AB的中点,AD,CE相交于G.求证:AG=2DG.
解:连ED,则ED∥AC,且ED=证△DEG∽△ACG,
∴
20.(本题8分)如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
(1)若D(2,3),请在网格图中画出一个格点△DEF,使△DEF∽△ABC,且相似比为2:1;
(2)填空:DF的长是_________.
解:(1)略;
(2)DF=
21.(本题8分)如图,等边△ABC的边长是10,点E、F分别在AC、BC边上,AE=CF,连接AF、BE相交于点P.
(1)求∠APB的度数;
(2)若AE=6,求AP·AF的值.
解:(1)易证△ABE∽△CAF, 易求∠APB=120°
(2)证△APE∽△ACF,∴AP·AF=AE·AC=4×10=40.
22.(本题10分)如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO.并延长AO交⊙0于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若求 的值
解:(1)证OP垂直平分AB,△PAO≌△PBD即可
(2)∵ 故设OC=2x,AC=3x,由 得PC=
∴PO=PC+OC=易证∠ABE=90°,OC∥BE,
∴BE=2CO=4x,∴∴.
23.(本题10分)如图,矩形ABCD中,AB=6,AD=8,动点P从点D出发,以每秒5个单位的速度向点B匀速运动,同时动点Q从点A出发,以每秒4个单位的速度向点D匀速运动,运动的时间为t秒(0<t<2).
(1)如图1,连接CQ,当t为何值时CQ=BC;
(2)如图2,连接AP、BQ,若BQ⊥AP,求t的值.
解:(1)∵AQ=4t,AD=8,∴DQ=8-4t,
又∵AB=6,∴由勾股定理得,
∵CQ=BC,解得t=2-
(2)过P作PE⊥AD于E,∴AB∥PE,∴△DEP∽△DAB,∴
∴
∵∠ABQ+∠BAP=90°, ∠EAP+∠BAP=90°,∴∠ABQ=∠EAP∵∠AEP=∠BAQ,
∴△BAQ∽△AEP,∴即
24.(本题12分)如图1,过原点的抛物线y=-x2+b x的对称轴为x=2,直线y=kx+4与y轴,抛物线依次交于点D,E,F.
(1)求抛物线的解析式;
(2)若求k的值
(3)是否存在实数k,使得以EF为直径的圆恰好经过原点?若存在,求出k的值;若不存在,请说明理由
解:(1)y=-x2十4x
(2)过E作EM⊥OD于M,过F作FN⊥EM于N,由
得-x2+(4-k)x-4=0, +=4-k①,·=4②,
可得△DEM∽△FEN,=4,③由①②③即xE>0,
得=1,=4,+=5=4-k,k=-1;
3)作EP⊥OD于P,作FQ⊥y轴于Q、可得∠EOF=90°,∠PEO=∠QOF,
∵△OPE∽△FQO,∴∴-+4=
-·+4(+)-16=1 得=4,+=4-k,代入上式得,
-4+16-4k-16=1,k
第16题图
第15题图
图2
图1
第16题图
第15题图
图2
图1
21世纪教育网(www.21cnjy.com)
