34.人教版九年级下册月考数学试题(二)(含答案)
文档属性
| 名称 | 34.人教版九年级下册月考数学试题(二)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 568.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 19:56:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
34.九年级数学(下)月考(二)
(测试范围:第26章反比例函数~第27章相似 考试时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.一反比例函数的图象经过点(-2,4),则此函数的图象也经过点( )
A.(2,4) B.(-2,-4) C.(2,-4) D.(-4,-2)
2.已知函数y=的图象过点(-3,-2),则该函数的图象分别在( )
A.第二、三象限 B.第二、四象限 C.第一、三象限 D.第三、四象限
3.为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足解析式是V=Sh(V≠0),则S关于h的函数图象大致是( )
4.△ABC和△A'B'C'是相似图形,且面积之比为1:25,则△ABC和△A'B'C'的对应边AB和A'B'的比为( )
A.5:1 B.1:4 C.1:5 D.1:25
5.已知△MNP如图,则下列四个三角形中与△MNP相似的是( )
6.如图,线段CD两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(6,0),则点A的坐标为( )
A.(3,6) B.(2.5,5) C.(3,5) D.(2,6)
7.双曲线y=-上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y3<y1<y2 C.y2<y1<y3 D.y3<y2<y1
8.如图,身高1.8m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
A.4.8m B.6.4m C.8m D.9m
9.如图,双曲线y=与直线y=kx+b交于点M,N,且点M的坐标为(1,3),点N的纵坐标为-1,则关于x的方程=kx+b的解为( )
A.-3,1 B.-3,3 C.-1,1 D.-1,3
10.如图,△ABC中,AB=BC,∠ABC=90°,O为AC的中点,∠ACB的平分线交AB于M,交OB于点N,若CN=,则CM的长为( )
A.2 B.2 C. D.
二、填空题(每小题3分,共18分)
11.反比例函数y=的图象经过点(2,-4),则k的值为 .
12.已知正比例函数y=-4x与反比例函数y=的图象的一个交点坐标为(-1,4),则另一个交点的坐标为 .
13.若反比例函数y=的图象位于第一、三象限内,正比例函数y=(2k-9)x的图象过第二、四象限.则k的取值范围是 .
14.在比例尺1:6000 000的地图上,量得南京到北京的距离是20cm,这两地的实际距离是 km.
15.如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,=,若△CEF的面积为1,则△AEB的面积为 .
16.如图,直线y=-0.5x+2与x轴,y轴分别交于A,B两点,AC⊥AB,交双曲线y=(x>0)于点C,BC交x轴于点D,若S△ACD=2S△ABD,则k的值是 .
三、解答题(共8题,共72分)
17.(本题8分)已知反比例函数的图象与直线y=4x相交于点A(1,a),求这个反比例函数的解析式.
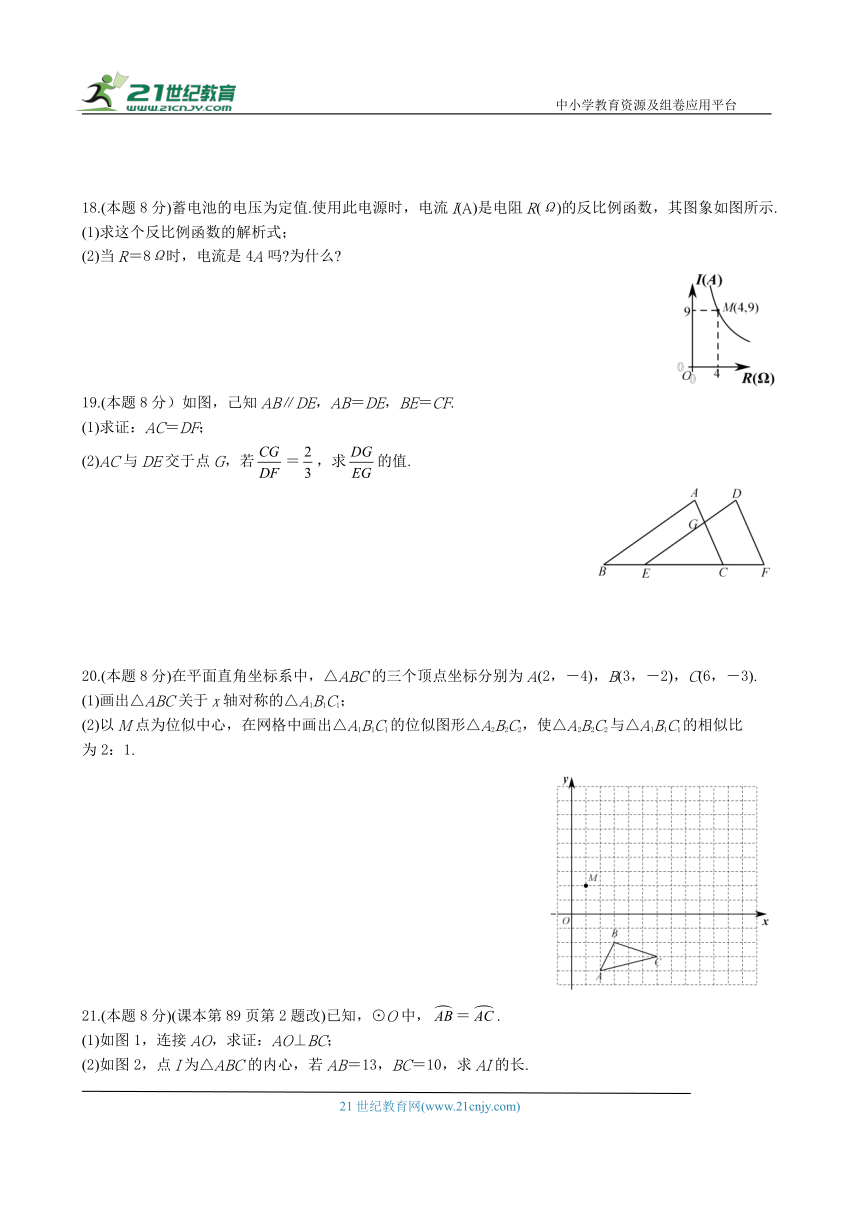
18.(本题8分)蓄电池的电压为定值.使用此电源时,电流I(A)是电阻R(Ω)的反比例函数,其图象如图所示.
(1)求这个反比例函数的解析式;
(2)当R=8Ω时,电流是4A吗 为什么
19.(本题8分)如图,己知AB∥DE,AB=DE,BE=CF.
(1)求证:AC=DF;
(2)AC与DE交于点G,若=,求的值.
20.(本题8分)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比
为2:1.
21.(本题8分)(课本第89页第2题改)已知,⊙O中,=.
(1)如图1,连接AO,求证:AO⊥BC;
(2)如图2,点I为△ABC的内心,若AB=13,BC=10,求AI的长.
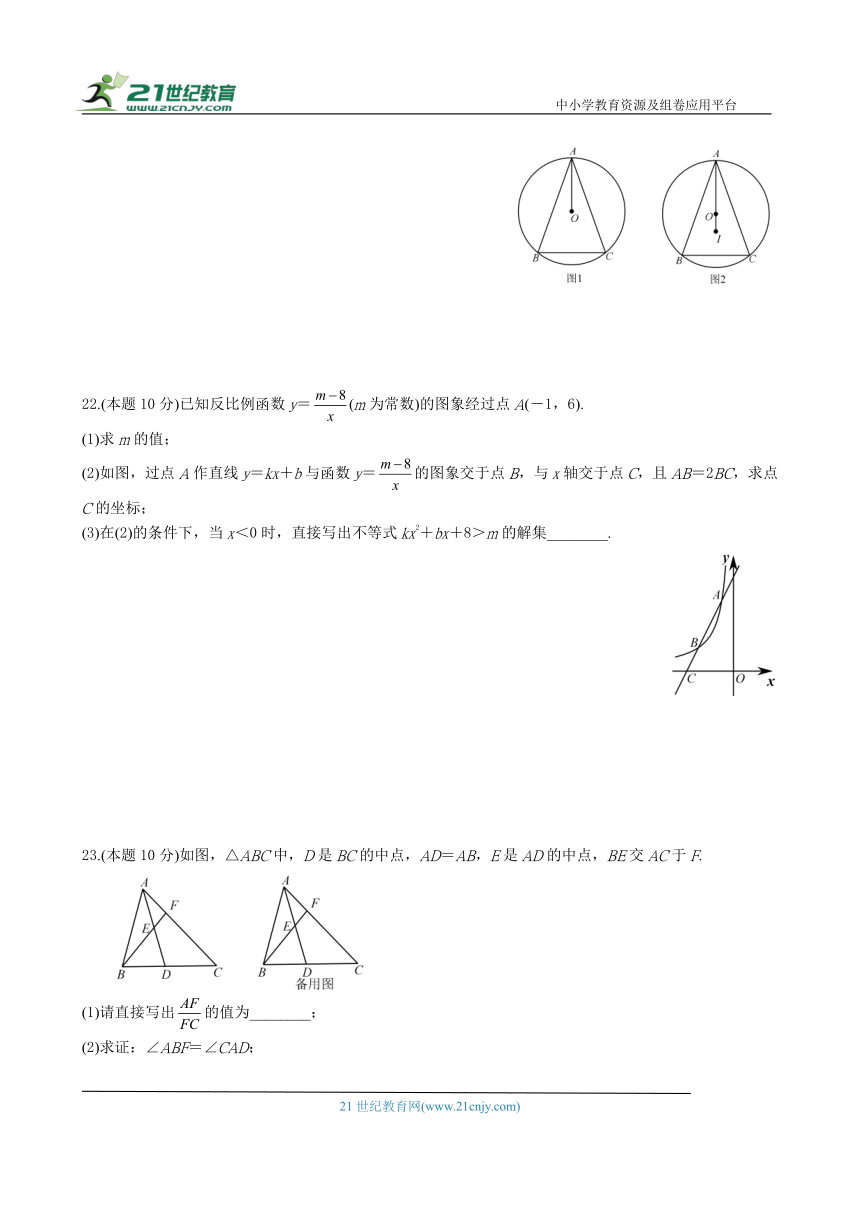
22.(本题10分)已知反比例函数y=(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图,过点A作直线y=kx+b与函数y=的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标;
(3)在(2)的条件下,当x<0时,直接写出不等式kx2+bx+8>m的解集________.
23.(本题10分)如图,△ABC中,D是BC的中点,AD=AB,E是AD的中点,BE交AC于F.
(1)请直接写出的值为________;
(2)求证:∠ABF=∠CAD;
(3)若EF=2,求AC的长.
24.(本题12分)已知抛物线y=-x2+x+交x轴于点A,B(点A在点B的左边),交y轴于点C,点D为抛物线的顶点.
(1)若直线y=x+m与此抛物线有唯一的公共点,求m的值;
(2)如图1,若点P在抛物线上,且∠PDB=∠ADC,求所有符合条件的点P的坐标;
(3)如图2,过C作CG∥x轴交抛物线于G,将图1中的直线AD向右平移得直线y=kx+b,交抛物线于E,F,交x轴于M,交CG于N.
①设E,F的横坐标分别为m,n,求的值;
②若EF=2MN,求b的值.
34.九年级数学(下)月考(二)
(测试范围:第26章反比例函数~第27章相似 考试时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.一反比例函数的图象经过点(-2,4),则此函数的图象也经过点( C )
A.(2,4) B.(-2,-4) C.(2,-4) D.(-4,-2)
2.已知函数y=的图象过点(-3,-2),则该函数的图象分别在( C )
A.第二、三象限 B.第二、四象限 C.第一、三象限 D.第三、四象限
3.为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足解析式是V=Sh(V≠0),则S关于h的函数图象大致是( C )
4.△ABC和△A'B'C'是相似图形,且面积之比为1:25,则△ABC和△A'B'C'的对应边AB和A'B'的比为( C )
A.5:1 B.1:4 C.1:5 D.1:25
5.已知△MNP如图,则下列四个三角形中与△MNP相似的是( D )
6.如图,线段CD两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(6,0),则点A的坐标为( A )
A.(3,6) B.(2.5,5) C.(3,5) D.(2,6)
7.双曲线y=-上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是( B )
A.y1<y2<y3 B.y3<y1<y2 C.y2<y1<y3 D.y3<y2<y1
8.如图,身高1.8m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( D )
A.4.8m B.6.4m C.8m D.9m
9.如图,双曲线y=与直线y=kx+b交于点M,N,且点M的坐标为(1,3),点N的纵坐标为-1,则关于x的方程=kx+b的解为( A )
A.-3,1 B.-3,3 C.-1,1 D.-1,3
10.如图,△ABC中,AB=BC,∠ABC=90°,O为AC的中点,∠ACB的平分线交AB于M,交OB于点N,若CN=,则CM的长为( D )
A.2 B.2 C. D.
二、填空题(每小题3分,共18分)
11.反比例函数y=的图象经过点(2,-4),则k的值为-8.
12.已知正比例函数y=-4x与反比例函数y=的图象的一个交点坐标为(-1,4),则另一个交点的坐标为(1,-4).
13.若反比例函数y=的图象位于第一、三象限内,正比例函数y=(2k-9)x的图象过第二、四象限.则k的取值范围是3<k<.
14.在比例尺1:6000 000的地图上,量得南京到北京的距离是20cm,这两地的实际距离是1200km.
15.如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,=,若△CEF的面积为1,则△AEB的面积为16.
16.如图,直线y=-0.5x+2与x轴,y轴分别交于A,B两点,AC⊥AB,交双曲线y=(x>0)于点C,BC交x轴于点D,若S△ACD=2S△ABD,则k的值是-8.
解:作CE⊥x轴于E,则是AE:CE=OB:OA=1:2,
又OB:CE=BD:CD=1:2.∴C(2,-4).∴k=-8.
三、解答题(共8题,共72分)
17.(本题8分)已知反比例函数的图象与直线y=4x相交于点A(1,a),求这个反比例函数的解析式.
解:将点A(1,a)代入直线y=4x得a=4×1=4.点A的坐标为(1,4),代入y=.
∴反比例函数的解析式为y=.
18.(本题8分)蓄电池的电压为定值.使用此电源时,电流I(A)是电阻R(Ω)的反比例函数,其图象如图所示.
(1)求这个反比例函数的解析式;
(2)当R=8Ω时,电流是4A吗 为什么
解:(1)电流I(A)是电阻R(Ω)的反比例函数,设I=(U≠0),把(4,9)代入,得U=4×9=36.∴I=.
(2)当R=100Ω时,I==4.5≠4,∴电流不可能是4A.
19.(本题8分)如图,己知AB∥DE,AB=DE,BE=CF.
(1)求证:AC=DF;
(2)AC与DE交于点G,若=,求的值.
解:(1)证△ABC≌△DEF即可;
(2).
20.(本题8分)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比
为2:1.
21.(本题8分)(课本第89页第2题改)已知,⊙O中,=.
(1)如图1,连接AO,求证:AO⊥BC;
(2)如图2,点I为△ABC的内心,若AB=13,BC=10,求AI的长.
解:(1)证△ABO≌△ACO,∠BAO=∠CAO即可.
(2)易知A,O,I共线,延长AO交BC于D.
∵AD⊥BC,∴BD=CD=5.
作IE⊥AB于E,则BE=BD=5,
∴AE=13-5=8.
∵△AIE∽△ABD,∴=,
∴=,∴AI=.
22.(本题10分)已知反比例函数y=(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图,过点A作直线y=kx+b与函数y=的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标;
(3)在(2)的条件下,当x<0时,直接写出不等式kx2+bx+8>m的解集________.
解:(1)m=2;
(2)分别过点A,B作x轴的垂线,垂足分别为点D,E,由题意得,AD=6,OD=1,
易知,AD∥BE,∴△CBE∽△CAD,
∵AB=2BC,∴CB:CA=BE:AD=1:3,∴BE=2,即点B的纵坐标为2,
当y=2时,x=-3,∴B(-3,2),
∴直线AB的解析式为y=2x+8,∴C(-4,0).
(3)由题意得kx2+bx>m-8,∵x<0,∴kx+b<,
看图知:x<-3或-1<x<0.
23.(本题10分)如图,△ABC中,D是BC的中点,AD=AB,E是AD的中点,BE交AC于F.
(1)请直接写出的值为________;
(2)求证:∠ABF=∠CAD;
(3)若EF=2,求AC的长.
解:⑴=;
(2)过A作BC的平行线交BF的延长线于G,
易证△AEG≌△BED,∴AG=BD=CD,
∵∠GAB+∠ABD=∠ADC+∠ADB=180°,∠GAB=∠ADC,
得△ABG≌△DAC,∴∠ABF=∠CAD.
(3)由(2)得∠G=∠GBC=∠C,
∴FB=FC.又AG∥BC,==,
∴FB=2AF=FC.设AF=a,
则BF=2a,△AFE∽△BFA,AF2=FE·FB,
∴a2=2×2a.∴a=4,而FC=2a=8,∴AC=12.
24.(本题12分)已知抛物线y=-x2+x+交x轴于点A,B(点A在点B的左边),交y轴于点C,点D为抛物线的顶点.
(1)若直线y=x+m与此抛物线有唯一的公共点,求m的值;
(2)如图1,若点P在抛物线上,且∠PDB=∠ADC,求所有符合条件的点P的坐标;
(3)如图2,过C作CG∥x轴交抛物线于G,将图1中的直线AD向右平移得直线y=kx+b,交抛物线于E,F,交x轴于M,交CG于N.
①设E,F的横坐标分别为m,n,求的值;
②若EF=2MN,求b的值.
解:(1)由△=0得m=.
(2)由对称性得P1(2,),设PD交线段AB于K,对称轴交x轴于H.作DQ⊥y轴,
可证∠ADB=90°,∴DC⊥PD,△DQC∽△DHK得HK=1,K(2,0),
直线PD为y=-2x+4,与抛物线联立求得P2(5,-6);
(3)①A(-1,0),D(1,2),直线AD为y=x+1,
依题意设直线EF为y=x+b,点F(n,n+b),E(m,m+b),
由y=-x2+x+和y=x+b得:m+n=0.∴=-1.
②作FQ⊥x轴,EQ⊥x轴,NH⊥y轴于H,
易证△MNH∽△EFQ,∴FQ=2NH=3,
∴(n+b)-(m+b)=3,∴n-m=3,
又由①知mn=2b-3,∴(m+n)2-4mn=9,
∴-4(2b-3)=9,∴b=.
21世纪教育网(www.21cnjy.com)
34.九年级数学(下)月考(二)
(测试范围:第26章反比例函数~第27章相似 考试时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.一反比例函数的图象经过点(-2,4),则此函数的图象也经过点( )
A.(2,4) B.(-2,-4) C.(2,-4) D.(-4,-2)
2.已知函数y=的图象过点(-3,-2),则该函数的图象分别在( )
A.第二、三象限 B.第二、四象限 C.第一、三象限 D.第三、四象限
3.为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足解析式是V=Sh(V≠0),则S关于h的函数图象大致是( )
4.△ABC和△A'B'C'是相似图形,且面积之比为1:25,则△ABC和△A'B'C'的对应边AB和A'B'的比为( )
A.5:1 B.1:4 C.1:5 D.1:25
5.已知△MNP如图,则下列四个三角形中与△MNP相似的是( )
6.如图,线段CD两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(6,0),则点A的坐标为( )
A.(3,6) B.(2.5,5) C.(3,5) D.(2,6)
7.双曲线y=-上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y3<y1<y2 C.y2<y1<y3 D.y3<y2<y1
8.如图,身高1.8m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
A.4.8m B.6.4m C.8m D.9m
9.如图,双曲线y=与直线y=kx+b交于点M,N,且点M的坐标为(1,3),点N的纵坐标为-1,则关于x的方程=kx+b的解为( )
A.-3,1 B.-3,3 C.-1,1 D.-1,3
10.如图,△ABC中,AB=BC,∠ABC=90°,O为AC的中点,∠ACB的平分线交AB于M,交OB于点N,若CN=,则CM的长为( )
A.2 B.2 C. D.
二、填空题(每小题3分,共18分)
11.反比例函数y=的图象经过点(2,-4),则k的值为 .
12.已知正比例函数y=-4x与反比例函数y=的图象的一个交点坐标为(-1,4),则另一个交点的坐标为 .
13.若反比例函数y=的图象位于第一、三象限内,正比例函数y=(2k-9)x的图象过第二、四象限.则k的取值范围是 .
14.在比例尺1:6000 000的地图上,量得南京到北京的距离是20cm,这两地的实际距离是 km.
15.如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,=,若△CEF的面积为1,则△AEB的面积为 .
16.如图,直线y=-0.5x+2与x轴,y轴分别交于A,B两点,AC⊥AB,交双曲线y=(x>0)于点C,BC交x轴于点D,若S△ACD=2S△ABD,则k的值是 .
三、解答题(共8题,共72分)
17.(本题8分)已知反比例函数的图象与直线y=4x相交于点A(1,a),求这个反比例函数的解析式.
18.(本题8分)蓄电池的电压为定值.使用此电源时,电流I(A)是电阻R(Ω)的反比例函数,其图象如图所示.
(1)求这个反比例函数的解析式;
(2)当R=8Ω时,电流是4A吗 为什么
19.(本题8分)如图,己知AB∥DE,AB=DE,BE=CF.
(1)求证:AC=DF;
(2)AC与DE交于点G,若=,求的值.
20.(本题8分)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比
为2:1.
21.(本题8分)(课本第89页第2题改)已知,⊙O中,=.
(1)如图1,连接AO,求证:AO⊥BC;
(2)如图2,点I为△ABC的内心,若AB=13,BC=10,求AI的长.
22.(本题10分)已知反比例函数y=(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图,过点A作直线y=kx+b与函数y=的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标;
(3)在(2)的条件下,当x<0时,直接写出不等式kx2+bx+8>m的解集________.
23.(本题10分)如图,△ABC中,D是BC的中点,AD=AB,E是AD的中点,BE交AC于F.
(1)请直接写出的值为________;
(2)求证:∠ABF=∠CAD;
(3)若EF=2,求AC的长.
24.(本题12分)已知抛物线y=-x2+x+交x轴于点A,B(点A在点B的左边),交y轴于点C,点D为抛物线的顶点.
(1)若直线y=x+m与此抛物线有唯一的公共点,求m的值;
(2)如图1,若点P在抛物线上,且∠PDB=∠ADC,求所有符合条件的点P的坐标;
(3)如图2,过C作CG∥x轴交抛物线于G,将图1中的直线AD向右平移得直线y=kx+b,交抛物线于E,F,交x轴于M,交CG于N.
①设E,F的横坐标分别为m,n,求的值;
②若EF=2MN,求b的值.
34.九年级数学(下)月考(二)
(测试范围:第26章反比例函数~第27章相似 考试时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1.一反比例函数的图象经过点(-2,4),则此函数的图象也经过点( C )
A.(2,4) B.(-2,-4) C.(2,-4) D.(-4,-2)
2.已知函数y=的图象过点(-3,-2),则该函数的图象分别在( C )
A.第二、三象限 B.第二、四象限 C.第一、三象限 D.第三、四象限
3.为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积S(m2)与其深度h(m)满足解析式是V=Sh(V≠0),则S关于h的函数图象大致是( C )
4.△ABC和△A'B'C'是相似图形,且面积之比为1:25,则△ABC和△A'B'C'的对应边AB和A'B'的比为( C )
A.5:1 B.1:4 C.1:5 D.1:25
5.已知△MNP如图,则下列四个三角形中与△MNP相似的是( D )
6.如图,线段CD两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(6,0),则点A的坐标为( A )
A.(3,6) B.(2.5,5) C.(3,5) D.(2,6)
7.双曲线y=-上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<x2<0<x3,则y1,y2,y3的大小关系是( B )
A.y1<y2<y3 B.y3<y1<y2 C.y2<y1<y3 D.y3<y2<y1
8.如图,身高1.8m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( D )
A.4.8m B.6.4m C.8m D.9m
9.如图,双曲线y=与直线y=kx+b交于点M,N,且点M的坐标为(1,3),点N的纵坐标为-1,则关于x的方程=kx+b的解为( A )
A.-3,1 B.-3,3 C.-1,1 D.-1,3
10.如图,△ABC中,AB=BC,∠ABC=90°,O为AC的中点,∠ACB的平分线交AB于M,交OB于点N,若CN=,则CM的长为( D )
A.2 B.2 C. D.
二、填空题(每小题3分,共18分)
11.反比例函数y=的图象经过点(2,-4),则k的值为-8.
12.已知正比例函数y=-4x与反比例函数y=的图象的一个交点坐标为(-1,4),则另一个交点的坐标为(1,-4).
13.若反比例函数y=的图象位于第一、三象限内,正比例函数y=(2k-9)x的图象过第二、四象限.则k的取值范围是3<k<.
14.在比例尺1:6000 000的地图上,量得南京到北京的距离是20cm,这两地的实际距离是1200km.
15.如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,=,若△CEF的面积为1,则△AEB的面积为16.
16.如图,直线y=-0.5x+2与x轴,y轴分别交于A,B两点,AC⊥AB,交双曲线y=(x>0)于点C,BC交x轴于点D,若S△ACD=2S△ABD,则k的值是-8.
解:作CE⊥x轴于E,则是AE:CE=OB:OA=1:2,
又OB:CE=BD:CD=1:2.∴C(2,-4).∴k=-8.
三、解答题(共8题,共72分)
17.(本题8分)已知反比例函数的图象与直线y=4x相交于点A(1,a),求这个反比例函数的解析式.
解:将点A(1,a)代入直线y=4x得a=4×1=4.点A的坐标为(1,4),代入y=.
∴反比例函数的解析式为y=.
18.(本题8分)蓄电池的电压为定值.使用此电源时,电流I(A)是电阻R(Ω)的反比例函数,其图象如图所示.
(1)求这个反比例函数的解析式;
(2)当R=8Ω时,电流是4A吗 为什么
解:(1)电流I(A)是电阻R(Ω)的反比例函数,设I=(U≠0),把(4,9)代入,得U=4×9=36.∴I=.
(2)当R=100Ω时,I==4.5≠4,∴电流不可能是4A.
19.(本题8分)如图,己知AB∥DE,AB=DE,BE=CF.
(1)求证:AC=DF;
(2)AC与DE交于点G,若=,求的值.
解:(1)证△ABC≌△DEF即可;
(2).
20.(本题8分)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比
为2:1.
21.(本题8分)(课本第89页第2题改)已知,⊙O中,=.
(1)如图1,连接AO,求证:AO⊥BC;
(2)如图2,点I为△ABC的内心,若AB=13,BC=10,求AI的长.
解:(1)证△ABO≌△ACO,∠BAO=∠CAO即可.
(2)易知A,O,I共线,延长AO交BC于D.
∵AD⊥BC,∴BD=CD=5.
作IE⊥AB于E,则BE=BD=5,
∴AE=13-5=8.
∵△AIE∽△ABD,∴=,
∴=,∴AI=.
22.(本题10分)已知反比例函数y=(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图,过点A作直线y=kx+b与函数y=的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标;
(3)在(2)的条件下,当x<0时,直接写出不等式kx2+bx+8>m的解集________.
解:(1)m=2;
(2)分别过点A,B作x轴的垂线,垂足分别为点D,E,由题意得,AD=6,OD=1,
易知,AD∥BE,∴△CBE∽△CAD,
∵AB=2BC,∴CB:CA=BE:AD=1:3,∴BE=2,即点B的纵坐标为2,
当y=2时,x=-3,∴B(-3,2),
∴直线AB的解析式为y=2x+8,∴C(-4,0).
(3)由题意得kx2+bx>m-8,∵x<0,∴kx+b<,
看图知:x<-3或-1<x<0.
23.(本题10分)如图,△ABC中,D是BC的中点,AD=AB,E是AD的中点,BE交AC于F.
(1)请直接写出的值为________;
(2)求证:∠ABF=∠CAD;
(3)若EF=2,求AC的长.
解:⑴=;
(2)过A作BC的平行线交BF的延长线于G,
易证△AEG≌△BED,∴AG=BD=CD,
∵∠GAB+∠ABD=∠ADC+∠ADB=180°,∠GAB=∠ADC,
得△ABG≌△DAC,∴∠ABF=∠CAD.
(3)由(2)得∠G=∠GBC=∠C,
∴FB=FC.又AG∥BC,==,
∴FB=2AF=FC.设AF=a,
则BF=2a,△AFE∽△BFA,AF2=FE·FB,
∴a2=2×2a.∴a=4,而FC=2a=8,∴AC=12.
24.(本题12分)已知抛物线y=-x2+x+交x轴于点A,B(点A在点B的左边),交y轴于点C,点D为抛物线的顶点.
(1)若直线y=x+m与此抛物线有唯一的公共点,求m的值;
(2)如图1,若点P在抛物线上,且∠PDB=∠ADC,求所有符合条件的点P的坐标;
(3)如图2,过C作CG∥x轴交抛物线于G,将图1中的直线AD向右平移得直线y=kx+b,交抛物线于E,F,交x轴于M,交CG于N.
①设E,F的横坐标分别为m,n,求的值;
②若EF=2MN,求b的值.
解:(1)由△=0得m=.
(2)由对称性得P1(2,),设PD交线段AB于K,对称轴交x轴于H.作DQ⊥y轴,
可证∠ADB=90°,∴DC⊥PD,△DQC∽△DHK得HK=1,K(2,0),
直线PD为y=-2x+4,与抛物线联立求得P2(5,-6);
(3)①A(-1,0),D(1,2),直线AD为y=x+1,
依题意设直线EF为y=x+b,点F(n,n+b),E(m,m+b),
由y=-x2+x+和y=x+b得:m+n=0.∴=-1.
②作FQ⊥x轴,EQ⊥x轴,NH⊥y轴于H,
易证△MNH∽△EFQ,∴FQ=2NH=3,
∴(n+b)-(m+b)=3,∴n-m=3,
又由①知mn=2b-3,∴(m+n)2-4mn=9,
∴-4(2b-3)=9,∴b=.
21世纪教育网(www.21cnjy.com)
