35.九年级数学(下)第二十八章 锐角三角函数周练(一)(含答案)
文档属性
| 名称 | 35.九年级数学(下)第二十八章 锐角三角函数周练(一)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 280.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 19:47:52 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
35.九年级数学(下)第28章《三角函数》周练(一)
(考试范围:28.1锐角三角函数 解答参考时间:90分钟 满分120分)
一、选择题(每小题3分,共30分)
1.sin45°的值是( )
A.1 B. C. D.
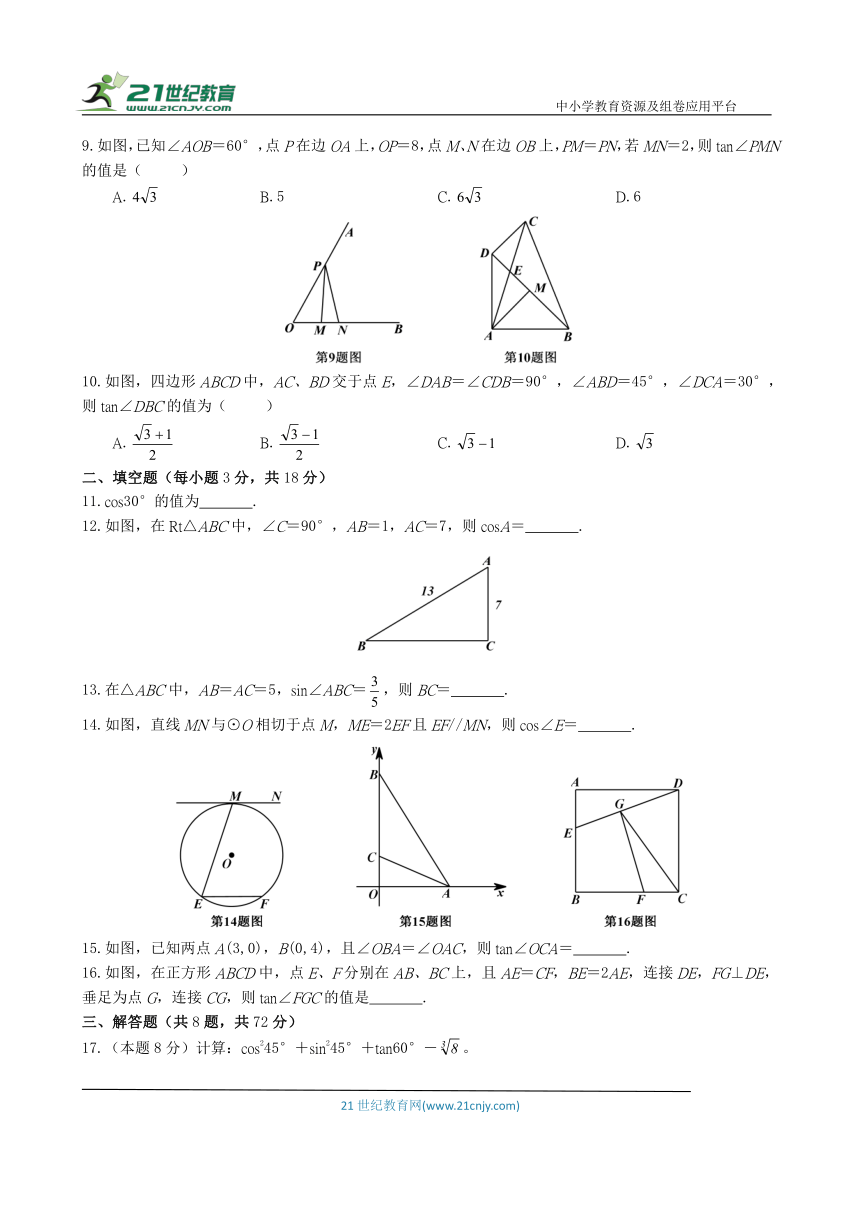
2.如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
A. B. C. D.2
3.如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,BC=10,tanB=2,则AC=( )
A.10 B.5 C.20 D.
5.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数的值正确的是( )
A.tanA= B.tanB= C.cosA= D.sinA=
6.如图,直径为4的⊙A经过点C(0,3)和点O(0,0),B是y轴右侧⊙A优弧上一点,sin∠OBC等于( )
A. B. C. D.
7.如图,在网格中,小正方形的边长均为1,点A、B、C都在格点上,tan∠ABC的值是( )
A. B. C. D.2
8.菱形OABC在平面直角坐标系中的位置如图所示,cos∠AOC=,OC=,则点B的坐标为( )A.(,1) B.(,1) C.(1, ) D.(1, )
9.如图,已知∠AOB=60°,点P在边OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则tan∠PMN的值是( )
A. B.5 C. D.6
10.如图,四边形ABCD中,AC、BD交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,则tan∠DBC的值为( )
A. B. C. D.
二、填空题(每小题3分,共18分)
11.cos30°的值为 .
12.如图,在Rt△ABC中,∠C=90°,AB=1,AC=7,则cosA= .
13.在△ABC中,AB=AC=5,sin∠ABC=,则BC= .
14.如图,直线MN与⊙O相切于点M,ME=2EF且EF//MN,则cos∠E= .
15.如图,已知两点A(3,0),B(0,4),且∠OBA=∠OAC,则tan∠OCA= .
16.如图,在正方形ABCD中,点E、F分别在AB、BC上,且AE=CF,BE=2AE,连接DE,FG⊥DE,垂足为点G,连接CG,则tan∠FGC的值是 .
三、解答题(共8题,共72分)
17.(本题8分)计算:cos245°+sin245°+tan60°-。
18.(本题8分)在△ABC中,若∠A、∠B满足,求∠C的大小。
19.(本题8分)如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,sinα=,求t的值。
20.(本题8分)如图,在△ABC中,AD为BC边上的高,AB=BC=20,cosB=,求AC的长。
21.(本题8分)【已知】对于同一锐角α总满足sin2α+cos2α=1。
【应用】已知锐角A满足sinA+cosA=,求sinA·cosA的值。
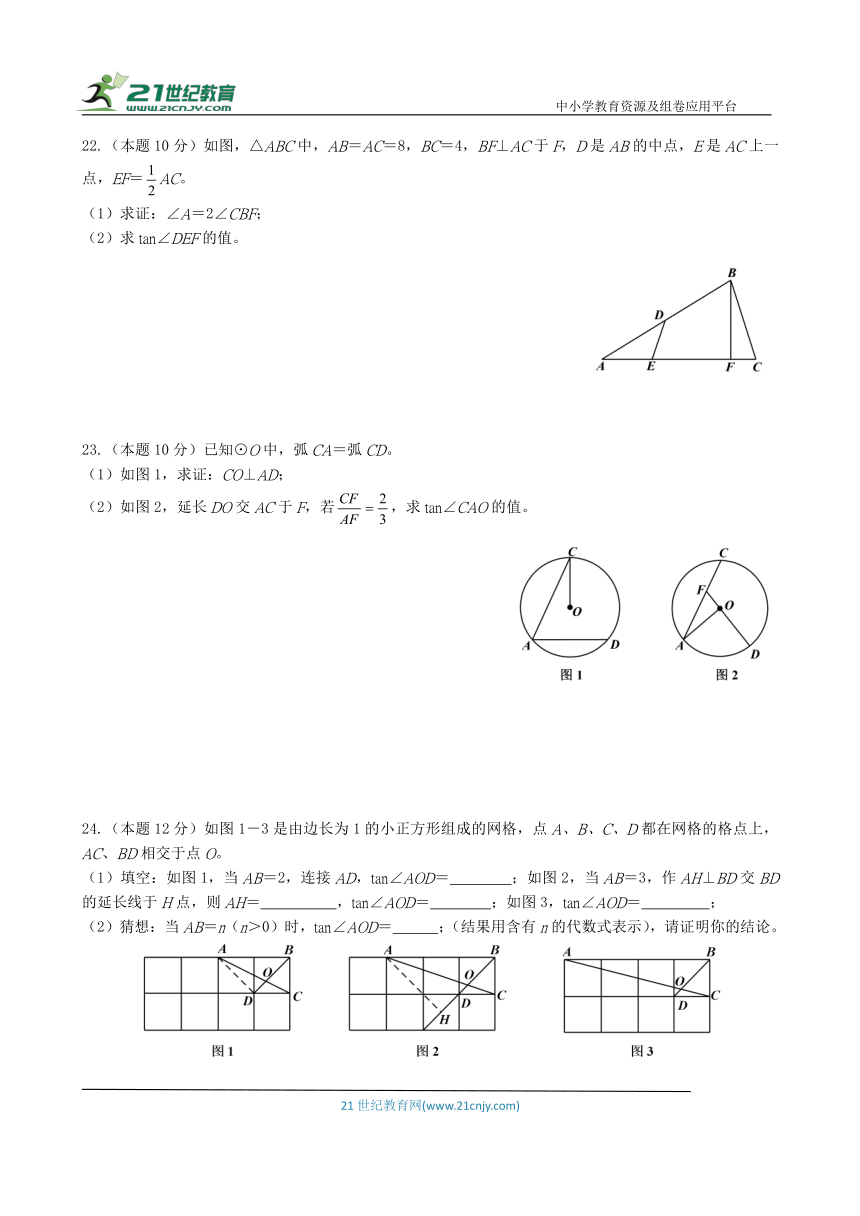
22.(本题10分)如图,△ABC中,AB=AC=8,BC=4,BF⊥AC于F,D是AB的中点,E是AC上一点,EF=AC。
(1)求证:∠A=2∠CBF;
(2)求tan∠DEF的值。
23.(本题10分)已知⊙O中,弧CA=弧CD。
(1)如图1,求证:CO⊥AD;
(2)如图2,延长DO交AC于F,若,求tan∠CAO的值。
24.(本题12分)如图1-3是由边长为1的小正方形组成的网格,点A、B、C、D都在网格的格点上,AC、BD相交于点O。
(1)填空:如图1,当AB=2,连接AD,tan∠AOD= ;如图2,当AB=3,作AH⊥BD交BD的延长线于H点,则AH= ,tan∠AOD= ;如图3,tan∠AOD= ;
(2)猜想:当AB=n(n>0)时,tan∠AOD= ;(结果用含有n的代数式表示),请证明你的结论。
35.九年级数学(下)第28章《三角函数》周练(一)
(考试范围:28.1锐角三角函数 解答参考时间:90分钟 满分120分)
一、选择题(每小题3分,共30分)
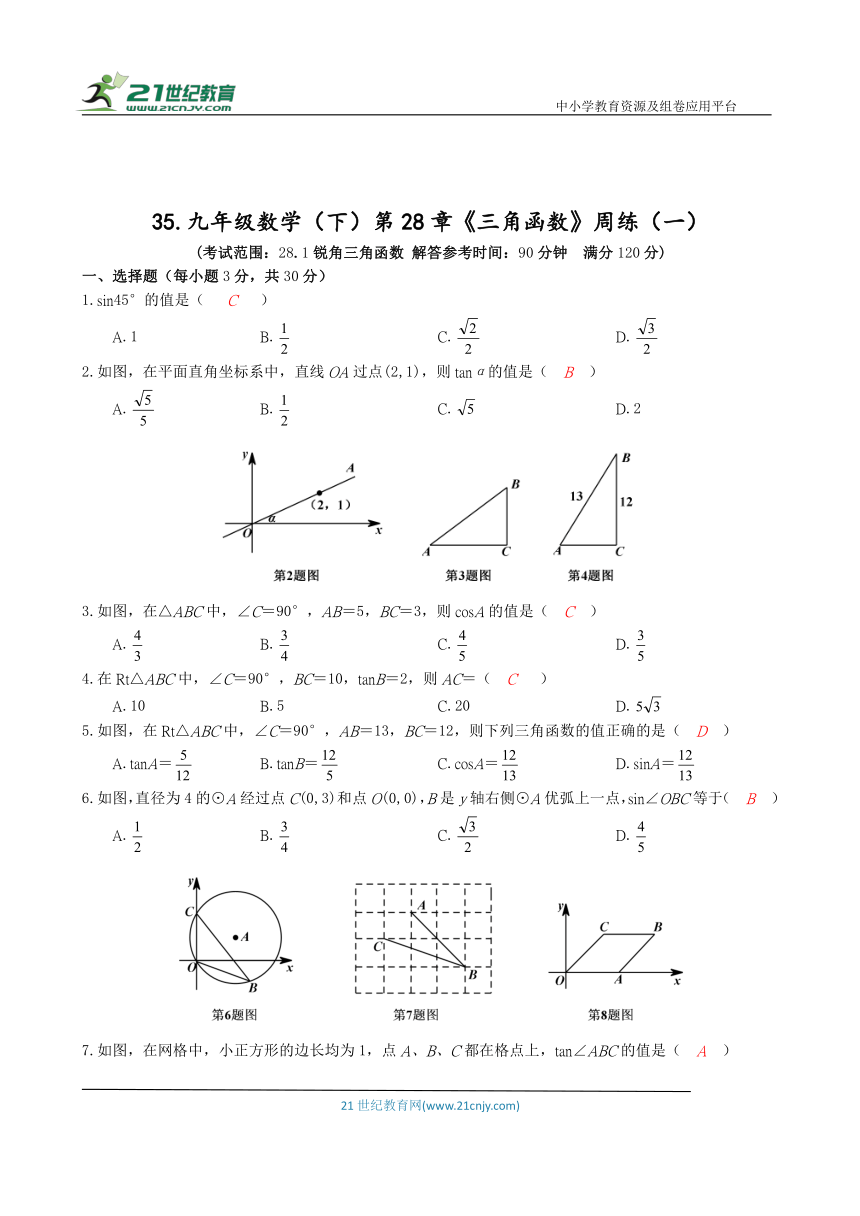
1.sin45°的值是( C )
A.1 B. C. D.
2.如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( B )
A. B. C. D.2
3.如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( C )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,BC=10,tanB=2,则AC=( C )
A.10 B.5 C.20 D.
5.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数的值正确的是( D )
A.tanA= B.tanB= C.cosA= D.sinA=
6.如图,直径为4的⊙A经过点C(0,3)和点O(0,0),B是y轴右侧⊙A优弧上一点,sin∠OBC等于( B )
A. B. C. D.
7.如图,在网格中,小正方形的边长均为1,点A、B、C都在格点上,tan∠ABC的值是( A )
A. B. C. D.2
8.菱形OABC在平面直角坐标系中的位置如图所示,cos∠AOC=,OC=,则点B的坐标为( A )A.(,1) B.(,1) C.(1, ) D.(1, )
9.如图,已知∠AOB=60°,点P在边OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则tan∠PMN的值是( A )
A. B.5 C. D.6
10.如图,四边形ABCD中,AC、BD交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,则tan∠DBC的值为( B )
A. B. C. D.
二、填空题(每小题3分,共18分)
11.cos30°的值为 。
12.如图,在Rt△ABC中,∠C=90°,AB=1,AC=7,则cosA= 。
13.在△ABC中,AB=AC=5,sin∠ABC=,则BC= 8 。
14.如图,直线MN与⊙O相切于点M,ME=2EF且EF//MN,则cos∠E= 。
15.如图,已知两点A(3,0),B(0,4),且∠OBA=∠OAC,则tan∠OCA= 。
16.如图,在正方形ABCD中,点E、F分别在AB、BC上,且AE=CF,BE=2AE,连接DE,FG⊥DE,垂足为点G,连接CG,则tan∠FGC的值是 。
解:延长GF交DC的延长线于点M,设正方形ABCD的边长为3a,
∵AE=CF,BE=2AE,∴AE=CF=a,AD=CD=3a,
易证△AED≌△CFM,∴AD=CM=3a,
在Rt△DGM中,∵CD=CM=3a,∴CG为斜边DM上的中线,
∴CG=CM,∴∠FGC=∠M,在Rt△FCM中,tan∠M=。
三、解答题(共8题,共72分)
17.(本题8分)计算:cos245°+sin245°+tan60°-。
解: 。
18.(本题8分)在△ABC中,若∠A、∠B满足,求∠C的大小。
解:∠A=45°,∠B=45°,∴∠C=90°。
19.(本题8分)如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,sinα=,求t的值。
解:t=3。
20.(本题8分)如图,在△ABC中,AD为BC边上的高,AB=BC=20,cosB=,求AC的长。
解:AC=。
21.(本题8分)【已知】对于同一锐角α总满足sin2α+cos2α=1。
【应用】已知锐角A满足sinA+cosA=,求sinA·cosA的值。
解:sinA·cosA=。
22.(本题10分)如图,△ABC中,AB=AC=8,BC=4,BF⊥AC于F,D是AB的中点,E是AC上一点,EF=AC。
(1)求证:∠A=2∠CBF;
(2)求tan∠DEF的值。
解:(1)略;
(2)提示:过B作BG//DE交AC于G,则AE=EG,FG=FC,
∴BF垂直平分CG,∴BG=BC,
∴∠DEF=∠BGF=∠C,
过A作AH⊥BC于H,则CH=BH=2,∴AH=2,
∴tan∠DEF=tan∠C=。
23.(本题10分)已知⊙O中,弧CA=弧CD。
(1)如图1,求证:CO⊥AD;
(2)如图2,延长DO交AC于F,若,求tan∠CAO的值。
解:(1)连CD、OA、OD,
证△OAC≌△ODC,∴OC平分∠ACD,
∵CA=CD,∴CO⊥AD。
(2)连AD,延长CO交AD于M,由(1)知CM⊥AD,延长DF交⊙O于N,连NA,
∵DN为直径,∴NA⊥AD,∴NA//CM,∴,
设AN=6,OC=4=OA,易证OM=AN=3,
∴AM=,
∴tan∠CAO=tan∠ACO=。
24.(本题12分)如图1-3是由边长为1的小正方形组成的网格,点A、B、C、D都在网格的格点上,AC、BD相交于点O。
(1)填空:如图1,当AB=2,连接AD,tan∠AOD= ;如图2,当AB=3,作AH⊥BD交BD的延长线于H点,则AH= ,tan∠AOD= ;如图3,tan∠AOD= ;
(2)猜想:当AB=n(n>0)时,tan∠AOD= ;(结果用含有n的代数式表示),请证明你的结论。
解:(1)图1中,∠ADO=90°,tan∠ADO=3,
图2中,AH=,tan∠AOD=2,
图3中,OB=,tan∠AOD=;
(2)tan∠AOD=,过A作AH⊥BD交BD的延长线于H,则AH=BH=,
∵AB//DC,∴,∴,
∴OH=,
∴tan∠AOD=。
21世纪教育网(www.21cnjy.com)
35.九年级数学(下)第28章《三角函数》周练(一)
(考试范围:28.1锐角三角函数 解答参考时间:90分钟 满分120分)
一、选择题(每小题3分,共30分)
1.sin45°的值是( )
A.1 B. C. D.
2.如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
A. B. C. D.2
3.如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,BC=10,tanB=2,则AC=( )
A.10 B.5 C.20 D.
5.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数的值正确的是( )
A.tanA= B.tanB= C.cosA= D.sinA=
6.如图,直径为4的⊙A经过点C(0,3)和点O(0,0),B是y轴右侧⊙A优弧上一点,sin∠OBC等于( )
A. B. C. D.
7.如图,在网格中,小正方形的边长均为1,点A、B、C都在格点上,tan∠ABC的值是( )
A. B. C. D.2
8.菱形OABC在平面直角坐标系中的位置如图所示,cos∠AOC=,OC=,则点B的坐标为( )A.(,1) B.(,1) C.(1, ) D.(1, )
9.如图,已知∠AOB=60°,点P在边OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则tan∠PMN的值是( )
A. B.5 C. D.6
10.如图,四边形ABCD中,AC、BD交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,则tan∠DBC的值为( )
A. B. C. D.
二、填空题(每小题3分,共18分)
11.cos30°的值为 .
12.如图,在Rt△ABC中,∠C=90°,AB=1,AC=7,则cosA= .
13.在△ABC中,AB=AC=5,sin∠ABC=,则BC= .
14.如图,直线MN与⊙O相切于点M,ME=2EF且EF//MN,则cos∠E= .
15.如图,已知两点A(3,0),B(0,4),且∠OBA=∠OAC,则tan∠OCA= .
16.如图,在正方形ABCD中,点E、F分别在AB、BC上,且AE=CF,BE=2AE,连接DE,FG⊥DE,垂足为点G,连接CG,则tan∠FGC的值是 .
三、解答题(共8题,共72分)
17.(本题8分)计算:cos245°+sin245°+tan60°-。
18.(本题8分)在△ABC中,若∠A、∠B满足,求∠C的大小。
19.(本题8分)如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,sinα=,求t的值。
20.(本题8分)如图,在△ABC中,AD为BC边上的高,AB=BC=20,cosB=,求AC的长。
21.(本题8分)【已知】对于同一锐角α总满足sin2α+cos2α=1。
【应用】已知锐角A满足sinA+cosA=,求sinA·cosA的值。
22.(本题10分)如图,△ABC中,AB=AC=8,BC=4,BF⊥AC于F,D是AB的中点,E是AC上一点,EF=AC。
(1)求证:∠A=2∠CBF;
(2)求tan∠DEF的值。
23.(本题10分)已知⊙O中,弧CA=弧CD。
(1)如图1,求证:CO⊥AD;
(2)如图2,延长DO交AC于F,若,求tan∠CAO的值。
24.(本题12分)如图1-3是由边长为1的小正方形组成的网格,点A、B、C、D都在网格的格点上,AC、BD相交于点O。
(1)填空:如图1,当AB=2,连接AD,tan∠AOD= ;如图2,当AB=3,作AH⊥BD交BD的延长线于H点,则AH= ,tan∠AOD= ;如图3,tan∠AOD= ;
(2)猜想:当AB=n(n>0)时,tan∠AOD= ;(结果用含有n的代数式表示),请证明你的结论。
35.九年级数学(下)第28章《三角函数》周练(一)
(考试范围:28.1锐角三角函数 解答参考时间:90分钟 满分120分)
一、选择题(每小题3分,共30分)
1.sin45°的值是( C )
A.1 B. C. D.
2.如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( B )
A. B. C. D.2
3.如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( C )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,BC=10,tanB=2,则AC=( C )
A.10 B.5 C.20 D.
5.如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数的值正确的是( D )
A.tanA= B.tanB= C.cosA= D.sinA=
6.如图,直径为4的⊙A经过点C(0,3)和点O(0,0),B是y轴右侧⊙A优弧上一点,sin∠OBC等于( B )
A. B. C. D.
7.如图,在网格中,小正方形的边长均为1,点A、B、C都在格点上,tan∠ABC的值是( A )
A. B. C. D.2
8.菱形OABC在平面直角坐标系中的位置如图所示,cos∠AOC=,OC=,则点B的坐标为( A )A.(,1) B.(,1) C.(1, ) D.(1, )
9.如图,已知∠AOB=60°,点P在边OA上,OP=8,点M、N在边OB上,PM=PN,若MN=2,则tan∠PMN的值是( A )
A. B.5 C. D.6
10.如图,四边形ABCD中,AC、BD交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,则tan∠DBC的值为( B )
A. B. C. D.
二、填空题(每小题3分,共18分)
11.cos30°的值为 。
12.如图,在Rt△ABC中,∠C=90°,AB=1,AC=7,则cosA= 。
13.在△ABC中,AB=AC=5,sin∠ABC=,则BC= 8 。
14.如图,直线MN与⊙O相切于点M,ME=2EF且EF//MN,则cos∠E= 。
15.如图,已知两点A(3,0),B(0,4),且∠OBA=∠OAC,则tan∠OCA= 。
16.如图,在正方形ABCD中,点E、F分别在AB、BC上,且AE=CF,BE=2AE,连接DE,FG⊥DE,垂足为点G,连接CG,则tan∠FGC的值是 。
解:延长GF交DC的延长线于点M,设正方形ABCD的边长为3a,
∵AE=CF,BE=2AE,∴AE=CF=a,AD=CD=3a,
易证△AED≌△CFM,∴AD=CM=3a,
在Rt△DGM中,∵CD=CM=3a,∴CG为斜边DM上的中线,
∴CG=CM,∴∠FGC=∠M,在Rt△FCM中,tan∠M=。
三、解答题(共8题,共72分)
17.(本题8分)计算:cos245°+sin245°+tan60°-。
解: 。
18.(本题8分)在△ABC中,若∠A、∠B满足,求∠C的大小。
解:∠A=45°,∠B=45°,∴∠C=90°。
19.(本题8分)如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,sinα=,求t的值。
解:t=3。
20.(本题8分)如图,在△ABC中,AD为BC边上的高,AB=BC=20,cosB=,求AC的长。
解:AC=。
21.(本题8分)【已知】对于同一锐角α总满足sin2α+cos2α=1。
【应用】已知锐角A满足sinA+cosA=,求sinA·cosA的值。
解:sinA·cosA=。
22.(本题10分)如图,△ABC中,AB=AC=8,BC=4,BF⊥AC于F,D是AB的中点,E是AC上一点,EF=AC。
(1)求证:∠A=2∠CBF;
(2)求tan∠DEF的值。
解:(1)略;
(2)提示:过B作BG//DE交AC于G,则AE=EG,FG=FC,
∴BF垂直平分CG,∴BG=BC,
∴∠DEF=∠BGF=∠C,
过A作AH⊥BC于H,则CH=BH=2,∴AH=2,
∴tan∠DEF=tan∠C=。
23.(本题10分)已知⊙O中,弧CA=弧CD。
(1)如图1,求证:CO⊥AD;
(2)如图2,延长DO交AC于F,若,求tan∠CAO的值。
解:(1)连CD、OA、OD,
证△OAC≌△ODC,∴OC平分∠ACD,
∵CA=CD,∴CO⊥AD。
(2)连AD,延长CO交AD于M,由(1)知CM⊥AD,延长DF交⊙O于N,连NA,
∵DN为直径,∴NA⊥AD,∴NA//CM,∴,
设AN=6,OC=4=OA,易证OM=AN=3,
∴AM=,
∴tan∠CAO=tan∠ACO=。
24.(本题12分)如图1-3是由边长为1的小正方形组成的网格,点A、B、C、D都在网格的格点上,AC、BD相交于点O。
(1)填空:如图1,当AB=2,连接AD,tan∠AOD= ;如图2,当AB=3,作AH⊥BD交BD的延长线于H点,则AH= ,tan∠AOD= ;如图3,tan∠AOD= ;
(2)猜想:当AB=n(n>0)时,tan∠AOD= ;(结果用含有n的代数式表示),请证明你的结论。
解:(1)图1中,∠ADO=90°,tan∠ADO=3,
图2中,AH=,tan∠AOD=2,
图3中,OB=,tan∠AOD=;
(2)tan∠AOD=,过A作AH⊥BD交BD的延长线于H,则AH=BH=,
∵AB//DC,∴,∴,
∴OH=,
∴tan∠AOD=。
21世纪教育网(www.21cnjy.com)
