36.九年级数学(下)第二十八章 锐角三角函数专题卷A—核心考点归纳一点通(含答案)
文档属性
| 名称 | 36.九年级数学(下)第二十八章 锐角三角函数专题卷A—核心考点归纳一点通(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 485.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
36.九年级(下)第28章《三角函数》专题卷A
核心考点归纳一点通
核心考点1 求锐角三角函数值
(一)根据锐角三角函数的定义求三角函数值
1.△ABC中,∠C=90°,BC=8,AB=10,求sinA、cosA、tanA的值.
2.如图,在Rt△ABC中,∠C=90°,tanA=,求sinA、cosB的值.
(二)根据线段关系求三角函数值
3.如图,在在Rt△ABC中,∠C=90°,D为斜边AB的中点,AC=5,CD=6.5,求sinA的值.
(三)根据点的坐标求三角函数值
4.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值.
(2)将△OAB平移得到△,点A的对应点是,点B的对应点的坐标为(2,-4),在坐标系中作出△,并直接写出、的坐标及sin∠OB的值.
核心考点2 特殊角与三角函数值
(一)特殊角的三角函数值的计算
5. 计算:sin60°= ;cos30°= ;tan45°= ;
6.在△ABC中,∠B=105°,∠C=30°,则cosA= .
7.计算:tan30°·tan45°·tan60°= .
8.计算(1)45°+tan60°·cos30°; (2)+tan30°
(二)已知三角函数值求角度
9.若∠为锐角,且cos(-10°)=,则∠的度数为 .
10.在△ABC中,∠A、∠B均为锐角,且tanA=,cosB=,试判断△ABC的形状.
核心考点3 解直角三角形
11.根据下列条件,求出Rt△ABC(∠C=90°)中未知的边和锐角.
(1)∠B=45°,AC=;
(2)BC=8,∠B=30°;
12.如图,在Rt△ABC中,已知∠C=90°,sinB=,AC=16,D为线段BC上一点,且CD=4.
(1)求BD的长;
(2)求tan∠ADC的值.
13.如图,斜面AC的坡度(CD与AD的比)为1:2,AC=米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,求旗杆BC的高度.
14.如图,△ABC中,∠B=45°,cos∠C=,AC=5,求△ABC的面积.
核心考点4 三角函数的应用
15.如图,在A处建筑物CD的顶端D的仰角为,且tan=,向前行进2米到达B处,从B处看D仰角为45°(图中各点均在同一平面内高度.,A、B、C三点在同一条直线上,DC⊥AC),求建筑物CD的高度.
16.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进60海里到达B点,此时,测得海岛C位于北偏东30°的方向,求海岛C到航线AB的距离CD.
17.在国际马拉松比赛过程中,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,求AB两点的距离.
核心考点5 圆与三角函数
(一)利用线段长求三角函数值
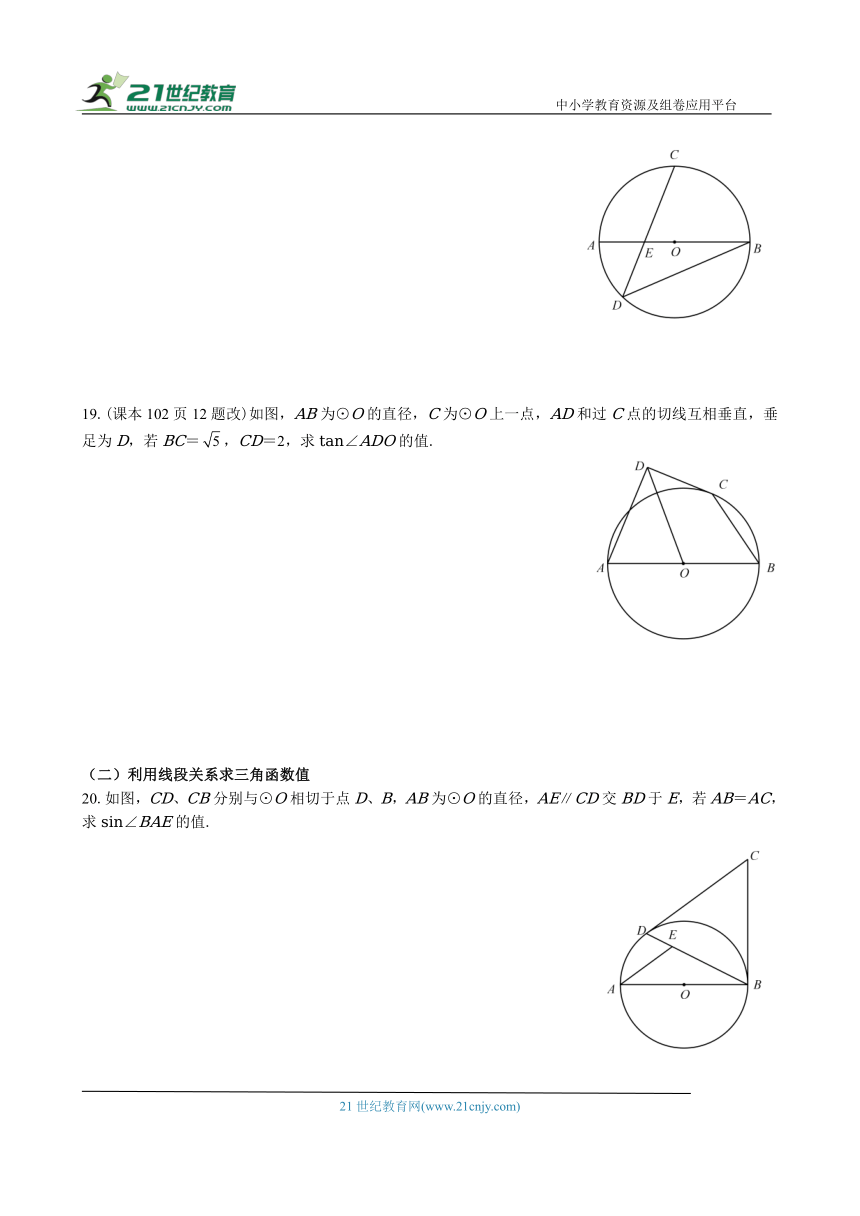
18.如图,AB为⊙O的直径,点C为的中点,弦CD 交OA于点E,DE=4,CE=5,求tan∠B的值.
19.(课本102页12题改)如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=,CD=2,求tan∠ADO的值.
(二)利用线段关系求三角函数值
20.如图,CD、CB分别与⊙O相切于点D、B,AB为⊙O的直径,AE∥CD交BD于E,若AB=AC,求sin∠BAE的值.
21.如图,在矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,=,△ECF的外接圆与AD相切,求tan∠DAF的值.
(三)利用三角形函数值求三角函数值
22.如图,⊙O中,=,D为上一点,且=,若cos∠BDC=,求tan∠ADC的值.
23.如图,以△ABC的一边AB为直径的⊙O与AC、BC分别交于D、E,且DE=BE,若cos∠C=,求cos∠AED的值.
36.九年级(下)第28章《三角函数》专题卷A
核心考点归纳一点通
核心考点1 求锐角三角函数值
(一)根据锐角三角函数的定义求三角函数值
(1)△ABC中,∠C=90°,BC=8,AB=10,求sinA、cosA、tanA的值.
解:,,.
2.如图,在Rt△ABC中,∠C=90°,tanA=,求sinA、cosB的值.
解:都为.
(二)根据线段关系求三角函数值
3.如图,在在Rt△ABC中,∠C=90°,D为斜边AB的中点,AC=5,CD=6.5,求sinA的值.
解:.
(三)根据点的坐标求三角函数值
4.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值.
(2)将△OAB平移得到△,点A的对应点是,点B的对应点的坐标为(2,-4),在坐标系中作出△,并直接写出、的坐标及sin∠OB的值.
解:(1)(2)图略,(-2,-6),(2,-6),sin∠OB=
核心考点2 特殊角与三角函数值
(1) 特殊角的三角函数值的计算
5. 计算:sin60°=;cos30°=;tan45°=1;
6.在△ABC中,∠B=105°,∠C=30°,则cosA=
7.计算:tan30°·tan45°·tan60°=1
8.计算(1)45°+tan60°·cos30°;
解:2.
(2)+tan30°
解:
(二)已知三角函数值求角度
9.若∠为锐角,且cos(-10°)=,则∠的度数为70°
10.在△ABC中,∠A、∠B均为锐角,且tanA=,cosB=,试判断△ABC的形状.
解:∠A=60°,∠B=30°,∠C=90°,△ABC为直角三角形.
核心考点3 解直角三角形
11.根据下列条件,求出Rt△ABC(∠C=90°)中未知的边和锐角.
(1)∠B=45°,AC=;
(2)BC=8,∠B=30°;
解:(1)∠A=45°,BC=,AB=.
(2)AC=,AB=,∠A=60°.
12.如图,在Rt△ABC中,已知∠C=90°,sinB=,AC=16,D为线段BC上一点,且CD=4.
(1)求BD的长;
(2)求tan∠ADC的值.
解(1)BD=8;(2)4.
13.如图,斜面AC的坡度(CD与AD的比)为1:2,AC=米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,求旗杆BC的高度.
解:5米.
14.如图,△ABC中,∠B=45°,cos∠C=,AC=5,求△ABC的面积.
解:.
核心考点4 三角函数的应用
15.如图,在A处建筑物CD的顶端D的仰角为,且tan=,向前行进2米到达B处,从B处看D仰角为45°(图中各点均在同一平面内高度.,A、B、C三点在同一条直线上,DC⊥AC),求建筑物CD的高度.
解:8米.
16.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进60海里到达B点,此时,测得海岛C位于北偏东30°的方向,求海岛C到航线AB的距离CD.
解:30海里.
17.在国际马拉松比赛过程中,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,求AB两点的距离.
解:(200+200)米
核心考点5 圆与三角函数
(1) 利用线段长求三角函数值
18.如图,AB为⊙O的直径,点C为的中点,弦CD 交OA于点E,DE=4,CE=5,求tan∠B的值.
解:连接CO,过D作DH⊥AB于H,
∴=,
设DH=4x,CO=5x,则AB=10x,
易证,
∴AH=2x,BH=8x,∴tan∠B===.
19.(课本102页12题改)如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=,CD=2,求tan∠ADO的值.
解:设AD交⊙O于E,易证AC平分∠BAD,BC=CE=,
∴DE=1,设OC交BE于M,则CM=1,BM=EM=CD=2,
设OB=R,在△OMB中,,R=,
∴tan∠ADO=tan∠DOC==
(2) 利用线段关系求三角函数值
20.如图,CD、CB分别与⊙O相切于点D、B,AB为⊙O的直径,AE∥CD交BD于E,若AB=AC,求sin∠BAE的值.
解:延长AE交⊙O于F,连接BF并延长交CD于G,
∵∠AFB=90°,∴BG⊥CD,
易证△ABF≌△BCG,设CG=BF=x,
设AB=BC=CD=1,则DG=1-x,
连接OD,易证AF=2DG=2(1-x)=2-2x,
在△ABF中有,,
解得,=1(舍),
∴sin∠BAE==.
21.如图,在矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,=,△ECF的外接圆与AD相切,求tan∠DAF的值.
解:过O作GH∥AB,分别交AD、BC于G、H,
∵∠AEF=90°,∴△ABE∽△ECF,
∵=,∴设BE=3a,AB=3b,
则CF=4a,EC=4b,OH=2a。OG=3b-2a,
易证,∴,化简得,
∴tan∠DAF===
(三)利用三角形函数值求三角函数值
22.如图,⊙O中,=,D为上一点,且=,若cos∠BDC=,求tan∠ADC的值.
解:连接AB交CD于E,连接OB交CD于F,易证OB⊥CD,
∵cos∠BDC==,故设CF=3,BC=4,∴BF=,
∵∠BEC=∠BAC+∠ACD,∠ABC=∠ACB=∠ACD+∠BCD,且∠BCD=∠BAC,
∴∠BFC=∠ABC,∴BC=EC,∴CE=4,∴EF=CE-CF=1,
∵BC=EC,∴∠ADC=∠ABC=∠BEC
∴tan∠ADC=tan∠BEC===
23.如图,以△ABC的一边AB为直径的⊙O与AC、BC分别交于D、E,且DE=BE,若cos∠C=,求cos∠AED的值.
解:∵DE=BE,∴=,∴∠DAE=∠BAE,∴AE⊥BC,∴AC=AB,∴CE=BE,
∵cosC==,∴设CE=BE=3x,AC=5x=AB,∴AE=4x,连接BD,则∠ADB=90°,
AC·BD=BC·AE,∴BD==,cos∠AED=cos∠ABD==.
21世纪教育网(www.21cnjy.com)
36.九年级(下)第28章《三角函数》专题卷A
核心考点归纳一点通
核心考点1 求锐角三角函数值
(一)根据锐角三角函数的定义求三角函数值
1.△ABC中,∠C=90°,BC=8,AB=10,求sinA、cosA、tanA的值.
2.如图,在Rt△ABC中,∠C=90°,tanA=,求sinA、cosB的值.
(二)根据线段关系求三角函数值
3.如图,在在Rt△ABC中,∠C=90°,D为斜边AB的中点,AC=5,CD=6.5,求sinA的值.
(三)根据点的坐标求三角函数值
4.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值.
(2)将△OAB平移得到△,点A的对应点是,点B的对应点的坐标为(2,-4),在坐标系中作出△,并直接写出、的坐标及sin∠OB的值.
核心考点2 特殊角与三角函数值
(一)特殊角的三角函数值的计算
5. 计算:sin60°= ;cos30°= ;tan45°= ;
6.在△ABC中,∠B=105°,∠C=30°,则cosA= .
7.计算:tan30°·tan45°·tan60°= .
8.计算(1)45°+tan60°·cos30°; (2)+tan30°
(二)已知三角函数值求角度
9.若∠为锐角,且cos(-10°)=,则∠的度数为 .
10.在△ABC中,∠A、∠B均为锐角,且tanA=,cosB=,试判断△ABC的形状.
核心考点3 解直角三角形
11.根据下列条件,求出Rt△ABC(∠C=90°)中未知的边和锐角.
(1)∠B=45°,AC=;
(2)BC=8,∠B=30°;
12.如图,在Rt△ABC中,已知∠C=90°,sinB=,AC=16,D为线段BC上一点,且CD=4.
(1)求BD的长;
(2)求tan∠ADC的值.
13.如图,斜面AC的坡度(CD与AD的比)为1:2,AC=米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,求旗杆BC的高度.
14.如图,△ABC中,∠B=45°,cos∠C=,AC=5,求△ABC的面积.
核心考点4 三角函数的应用
15.如图,在A处建筑物CD的顶端D的仰角为,且tan=,向前行进2米到达B处,从B处看D仰角为45°(图中各点均在同一平面内高度.,A、B、C三点在同一条直线上,DC⊥AC),求建筑物CD的高度.
16.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进60海里到达B点,此时,测得海岛C位于北偏东30°的方向,求海岛C到航线AB的距离CD.
17.在国际马拉松比赛过程中,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,求AB两点的距离.
核心考点5 圆与三角函数
(一)利用线段长求三角函数值
18.如图,AB为⊙O的直径,点C为的中点,弦CD 交OA于点E,DE=4,CE=5,求tan∠B的值.
19.(课本102页12题改)如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=,CD=2,求tan∠ADO的值.
(二)利用线段关系求三角函数值
20.如图,CD、CB分别与⊙O相切于点D、B,AB为⊙O的直径,AE∥CD交BD于E,若AB=AC,求sin∠BAE的值.
21.如图,在矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,=,△ECF的外接圆与AD相切,求tan∠DAF的值.
(三)利用三角形函数值求三角函数值
22.如图,⊙O中,=,D为上一点,且=,若cos∠BDC=,求tan∠ADC的值.
23.如图,以△ABC的一边AB为直径的⊙O与AC、BC分别交于D、E,且DE=BE,若cos∠C=,求cos∠AED的值.
36.九年级(下)第28章《三角函数》专题卷A
核心考点归纳一点通
核心考点1 求锐角三角函数值
(一)根据锐角三角函数的定义求三角函数值
(1)△ABC中,∠C=90°,BC=8,AB=10,求sinA、cosA、tanA的值.
解:,,.
2.如图,在Rt△ABC中,∠C=90°,tanA=,求sinA、cosB的值.
解:都为.
(二)根据线段关系求三角函数值
3.如图,在在Rt△ABC中,∠C=90°,D为斜边AB的中点,AC=5,CD=6.5,求sinA的值.
解:.
(三)根据点的坐标求三角函数值
4.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)求tan∠BOA的值.
(2)将△OAB平移得到△,点A的对应点是,点B的对应点的坐标为(2,-4),在坐标系中作出△,并直接写出、的坐标及sin∠OB的值.
解:(1)(2)图略,(-2,-6),(2,-6),sin∠OB=
核心考点2 特殊角与三角函数值
(1) 特殊角的三角函数值的计算
5. 计算:sin60°=;cos30°=;tan45°=1;
6.在△ABC中,∠B=105°,∠C=30°,则cosA=
7.计算:tan30°·tan45°·tan60°=1
8.计算(1)45°+tan60°·cos30°;
解:2.
(2)+tan30°
解:
(二)已知三角函数值求角度
9.若∠为锐角,且cos(-10°)=,则∠的度数为70°
10.在△ABC中,∠A、∠B均为锐角,且tanA=,cosB=,试判断△ABC的形状.
解:∠A=60°,∠B=30°,∠C=90°,△ABC为直角三角形.
核心考点3 解直角三角形
11.根据下列条件,求出Rt△ABC(∠C=90°)中未知的边和锐角.
(1)∠B=45°,AC=;
(2)BC=8,∠B=30°;
解:(1)∠A=45°,BC=,AB=.
(2)AC=,AB=,∠A=60°.
12.如图,在Rt△ABC中,已知∠C=90°,sinB=,AC=16,D为线段BC上一点,且CD=4.
(1)求BD的长;
(2)求tan∠ADC的值.
解(1)BD=8;(2)4.
13.如图,斜面AC的坡度(CD与AD的比)为1:2,AC=米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,求旗杆BC的高度.
解:5米.
14.如图,△ABC中,∠B=45°,cos∠C=,AC=5,求△ABC的面积.
解:.
核心考点4 三角函数的应用
15.如图,在A处建筑物CD的顶端D的仰角为,且tan=,向前行进2米到达B处,从B处看D仰角为45°(图中各点均在同一平面内高度.,A、B、C三点在同一条直线上,DC⊥AC),求建筑物CD的高度.
解:8米.
16.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进60海里到达B点,此时,测得海岛C位于北偏东30°的方向,求海岛C到航线AB的距离CD.
解:30海里.
17.在国际马拉松比赛过程中,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,求AB两点的距离.
解:(200+200)米
核心考点5 圆与三角函数
(1) 利用线段长求三角函数值
18.如图,AB为⊙O的直径,点C为的中点,弦CD 交OA于点E,DE=4,CE=5,求tan∠B的值.
解:连接CO,过D作DH⊥AB于H,
∴=,
设DH=4x,CO=5x,则AB=10x,
易证,
∴AH=2x,BH=8x,∴tan∠B===.
19.(课本102页12题改)如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=,CD=2,求tan∠ADO的值.
解:设AD交⊙O于E,易证AC平分∠BAD,BC=CE=,
∴DE=1,设OC交BE于M,则CM=1,BM=EM=CD=2,
设OB=R,在△OMB中,,R=,
∴tan∠ADO=tan∠DOC==
(2) 利用线段关系求三角函数值
20.如图,CD、CB分别与⊙O相切于点D、B,AB为⊙O的直径,AE∥CD交BD于E,若AB=AC,求sin∠BAE的值.
解:延长AE交⊙O于F,连接BF并延长交CD于G,
∵∠AFB=90°,∴BG⊥CD,
易证△ABF≌△BCG,设CG=BF=x,
设AB=BC=CD=1,则DG=1-x,
连接OD,易证AF=2DG=2(1-x)=2-2x,
在△ABF中有,,
解得,=1(舍),
∴sin∠BAE==.
21.如图,在矩形ABCD中,E为BC上一点,F为CD上一点,∠AEF=90°,=,△ECF的外接圆与AD相切,求tan∠DAF的值.
解:过O作GH∥AB,分别交AD、BC于G、H,
∵∠AEF=90°,∴△ABE∽△ECF,
∵=,∴设BE=3a,AB=3b,
则CF=4a,EC=4b,OH=2a。OG=3b-2a,
易证,∴,化简得,
∴tan∠DAF===
(三)利用三角形函数值求三角函数值
22.如图,⊙O中,=,D为上一点,且=,若cos∠BDC=,求tan∠ADC的值.
解:连接AB交CD于E,连接OB交CD于F,易证OB⊥CD,
∵cos∠BDC==,故设CF=3,BC=4,∴BF=,
∵∠BEC=∠BAC+∠ACD,∠ABC=∠ACB=∠ACD+∠BCD,且∠BCD=∠BAC,
∴∠BFC=∠ABC,∴BC=EC,∴CE=4,∴EF=CE-CF=1,
∵BC=EC,∴∠ADC=∠ABC=∠BEC
∴tan∠ADC=tan∠BEC===
23.如图,以△ABC的一边AB为直径的⊙O与AC、BC分别交于D、E,且DE=BE,若cos∠C=,求cos∠AED的值.
解:∵DE=BE,∴=,∴∠DAE=∠BAE,∴AE⊥BC,∴AC=AB,∴CE=BE,
∵cosC==,∴设CE=BE=3x,AC=5x=AB,∴AE=4x,连接BD,则∠ADB=90°,
AC·BD=BC·AE,∴BD==,cos∠AED=cos∠ABD==.
21世纪教育网(www.21cnjy.com)
