37.九年级数学(下)第二十八章 锐角三角函数单元检测卷(含答案)
文档属性
| 名称 | 37.九年级数学(下)第二十八章 锐角三角函数单元检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 340.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 19:48:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
37.九年级数学(下)第28章《三角函数》单元检测卷
(考试范围:第28.2~第28章全章综合测试 解得参考时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1. cos60°的值是( )
A. B. C. D.
2. 在△ABC中,∠C=90°,∠A=30°,则的值是( )
A.1 B. 2 C. D.
在△ABC中,∠C=90°,cos A=0.6,AC=6,则AB的长是( )
A. 14 B. 12 C. 10 D. 8
如图,AC是电杆的一根拉线,测得BC=3米,∠ACB=60°,则AB的长为( )
A. 米 B. 8米 C. 6米 D. 2米
第4题图 第5题图 第6题图
如图,为了测量河岸A,B两点的距离,与在AB垂直的方向上取点C,测得AC=,∠ABC=,那么AB等于( )
A. B. C. D.
如图,先锋村准备在坡角为的山坡上栽树,要求相邻两树之间的水平距离为4米,那么这两树在坡面上的距离AB为( )
A. B. C. D.
如图,河堤横断面积迎水坡AB的坡比是1:,堤高BC=10m,则坡面AB的长度是( )
A. 15m B. 20m C. m D. 10m
第7题图 第8题图 第9题图
如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
A. m B. m C. m D. m
如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=2,则AB的长为( )
A. B. C. D.
如图,在四边形ABCD中,∠A=∠C=45°,∠ADB=∠ABC=105°,若AB+CD=,则AB的长为( )
A. B. C. 2 D.
二、填空题(每小题3分,共18分)
11. 如图,在△ABC中,∠C=90°,AC=5,BC=3,则tan B的值是 .
第11题图 第12题图 第14题图
12.如图,方格纸中的每个小方格都是边长为1个单位长度的的正方形,每个小正方形的顶点叫格点. △ABC的顶点都在方格的格点上,则cos A= .
在△ABC中,若,则∠C的度数是 .
如图,在△ABC中,AB为⊙O的直径,∠ABC=50°,∠C=70°,则tan∠ODB= .
如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,tan∠CAM=,则tan∠B的值为 .
第15题图 第16题图
如图,在正方形ABCD外作等腰Rt△CDE,DE=CE,连结AE,则cos∠AED= .
三、解答题(共8题,共72分)
17.(本题8分)计算:.
18.(本题8分)如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=5,解这个直角三角形.
(本题8分)如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求cos C的值.
20.(本题8分)在△ABC中,AD是BC边上的高,∠C=45°,sin B=,AD=1,求BC的长.
21.(本题8分)如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离为米,若在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响. 问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
(本题10分)如图,AB为⊙O的直径,=,过点C作⊙O的切线交AB的延长线于E,连接BC,CD,AD.
(1)求证:∠BCE=∠BAD;
(2)若,求cos∠CBA的值.
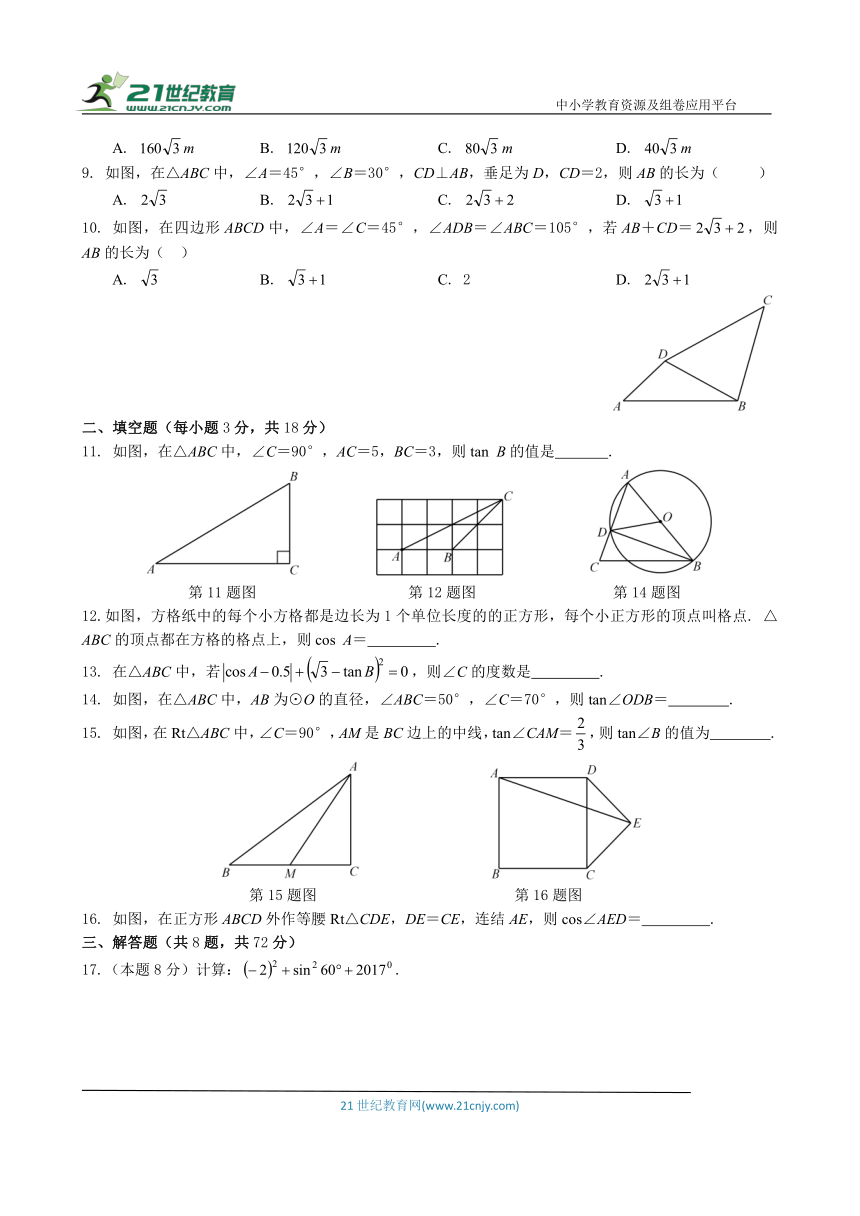
23.(本题10分)已知矩形ABCD中,E为BD上一点,EF⊥EC交AD于点F,FH⊥BD于点H.
(1)如图1,若AB=BC,猜想EH与CD的数量关系,并加以证明;
(2)如图2,若AB≠BC,敬爱喔ADB=,请探究EH与CD的数量关系.
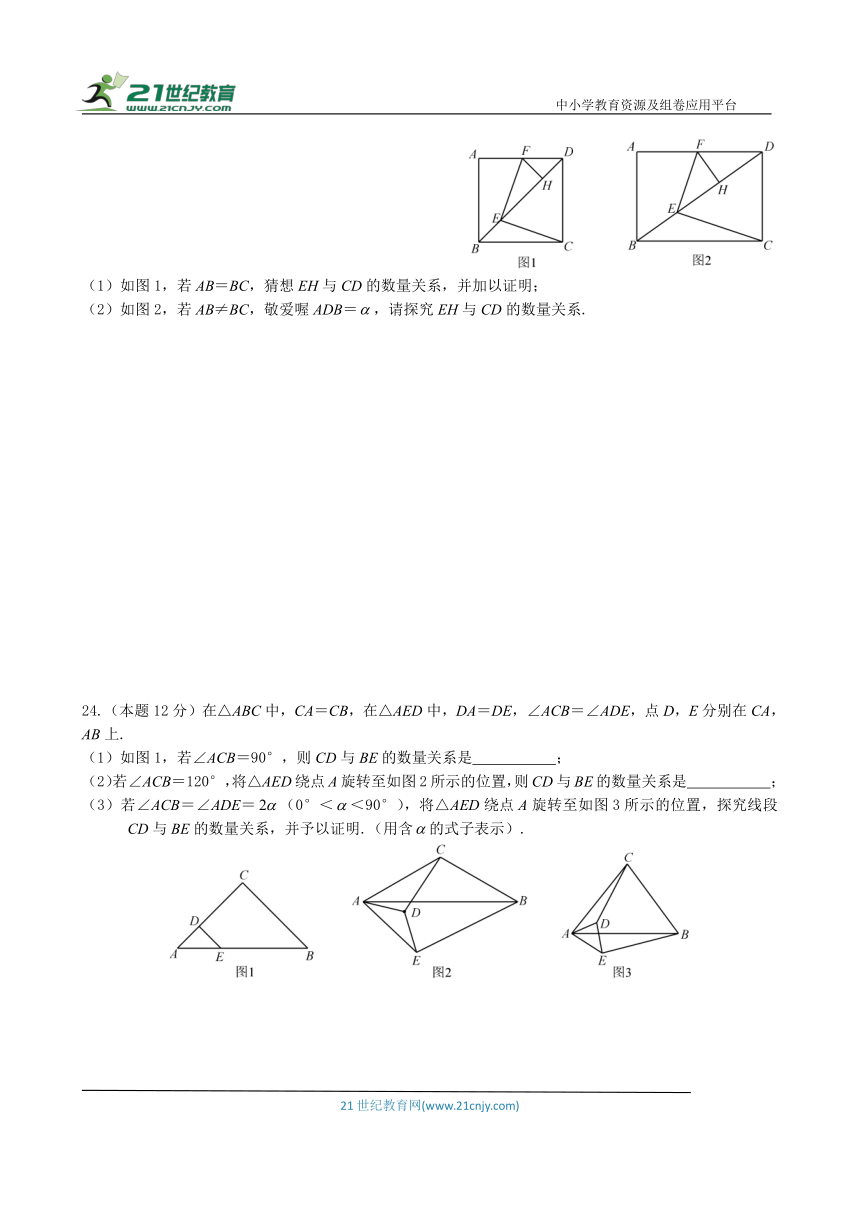
24.(本题12分)在△ABC中,CA=CB,在△AED中,DA=DE,∠ACB=∠ADE,点D,E分别在CA,AB上.
(1)如图1,若∠ACB=90°,则CD与BE的数量关系是 ;
(2)若∠ACB=120°,将△AED绕点A旋转至如图2所示的位置,则CD与BE的数量关系是 ;
(3)若∠ACB=∠ADE=(0°<<90°),将△AED绕点A旋转至如图3所示的位置,探究线段CD与BE的数量关系,并予以证明.(用含的式子表示).
37.九年级数学(下)第28章《三角函数》单元检测卷
(考试范围:第28.2~第28章全章综合测试 解得参考时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1. cos60°的值是( D )
A. B. C. D.
2. 在△ABC中,∠C=90°,∠A=30°,则的值是( C )
A.1 B. 2 C. D.
在△ABC中,∠C=90°,cos A=0.6,AC=6,则AB的长是( C )
A. 14 B. 12 C. 10 D. 8
如图,AC是电杆的一根拉线,测得BC=3米,∠ACB=60°,则AB的长为( A )
A. 米 B. 8米 C. 6米 D. 2米
第4题图 第5题图 第6题图
如图,为了测量河岸A,B两点的距离,与在AB垂直的方向上取点C,测得AC=,
∠ABC=,那么AB等于( C )
A. B. C. D.
如图,先锋村准备在坡角为的山坡上栽树,要求相邻两树之间的水平距离为4米,那
么这两树在坡面上的距离AB为( D )
A. B. C. D.
如图,河堤横断面积迎水坡AB的坡比是1:,堤高BC=10m,则坡面AB的长度是( B )
A. 15m B. 20m C. m D. 10m
第7题图 第8题图 第9题图
如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼
底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( A )
A. m B. m C. m D. m
如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=2,则AB的长为( C )
A. B. C. D.
如图,在四边形ABCD中,∠A=∠C=45°,∠ADB=∠ABC=105°,若AB+CD=,则AB的长为( B )
A. B. C. 2 D.
解:过D作DE⊥AB于E,过B作BF⊥CD于F,利用特殊角证明AB=CD.
二、填空题(每小题3分,共18分)
11. 如图,在△ABC中,∠C=90°,AC=5,BC=3,则tan B的值是 .
第11题图 第12题图 第14题图
12.如图,方格纸中的每个小方格都是边长为1个单位长度的的正方形,每个小正方形的顶点叫格点. △ABC的顶点都在方格的格点上,则cos A= .
在△ABC中,若,则∠C的度数是 60° .
如图,在△ABC中,AB为⊙O的直径,∠ABC=50°,∠C=70°,则tan∠ODB= .
如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,tan∠CAM=,则tan∠B的值为 .
第15题图 第16题图
如图,在正方形ABCD外作等腰Rt△CDE,DE=CE,连结AE,则cos∠AED= .
解:作AM⊥DE于M.
三、解答题(共8题,共72分)
17.(本题8分)计算:.
解:原式=.
18.(本题8分)如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=5,解这个直角三角形.
解:AB=10,BC=,∠A=60°.
(本题8分)如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求cos C的值.
解:∵在直角△ABD中,tan∠BAD=,
∴BD=AD · tan∠BAD=12×=9,
∴CD=BC-BD=14-9=5,
∴AC=,
∴.
20.(本题8分)在△ABC中,AD是BC边上的高,∠C=45°,sin B=,AD=1,求BC的长.
解:在Rt△ABD中,∵sin B=,
又∵AD=1,∴AB=3,
∵,
∴BD=,
在Rt△ADC中,∵∠C=45°,∴CD=AD=1,
∴BC=BD+DC=.
21.(本题8分)如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离为米,若在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响. 问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
解:过点C作CD⊥AB于D,∴BD=CD,AD=CD,
∵BD+AD=AB=(米),即,
∴CD=250,250米>200米.
答:在此路线段修建铁路,油库C不会受到影响.
(本题10分)如图,AB为⊙O的直径,=,过点C作⊙O的切线交AB的延长线于E,连接BC,CD,AD.
(1)求证:∠BCE=∠BAD;
(2)若,求cos∠CBA的值.
解:(1)连接AC,OC,∵=,∴∠BAC=∠DAC=∠OCA,
∵∠BCE+∠BCO=90°=∠OCA+∠BCO,∴∠BCE=∠OCA=∠BAD.
(2)延长BC,AD交于点F,∵∠BAC=∠DAC,∠BCA=90°,
∴AB=AF,BC=CF,设AB=AF=2R,
易证△CDF∽△ABF,∴,
设BC=CD=1,AD=2,
∴,∴R=(舍去负值),
∴AB=2R=,
∴cos∠CBA=.
23.(本题10分)已知矩形ABCD中,E为BD上一点,EF⊥EC交AD于点F,FH⊥BD于点H.
(1)如图1,若AB=BC,猜想EH与CD的数量关系,并加以证明;
(2)如图2,若AB≠BC,敬爱喔ADB=,请探究EH与CD的数量关系.
解:(1)EH=CD,作CG⊥BD于G,证△EHF≌△CGE.∴EH=CG=CD.
(2)作CG⊥BD于G,过E作MN⊥BC于N,交AD于M,易证△EHF∽△CGE
△EFM∽△CEN,∴ ①,∵ ②
①×②得,,∴EH=CD · sin.
24.(本题12分)在△ABC中,CA=CB,在△AED中,DA=DE,∠ACB=∠ADE,点D,E分别在CA,AB上.
(1)如图1,若∠ACB=90°,则CD与BE的数量关系是 ;
(2)若∠ACB=120°,将△AED绕点A旋转至如图2所示的位置,则CD与BE的数量关系是 ;
(3)若∠ACB=∠ADE=(0°<<90°),将△AED绕点A旋转至如图3所示的位置,探究线段CD与BE的数量关系,并予以证明.(用含的式子表示).
解:(1)BE=CD;
(2)BE=CD;
(3)BE=2CD · .
证明:如图,分别过点C、D作CM⊥AB于点M,DN⊥AE于点N,
∵CA=CB,DA=DE,∠ACB=∠ADE=,
∴∠CAB=∠DAE,∠ACM=∠ADN=,AM=AB,AN=AE,
∴∠CAD=∠BAE.
Rt△ACM和Rt△ADN中,sin∠ACM=,sin∠ADN=.
∴,又∠CAD=∠BAE. ∴△BAE∽△CAD,
∴,∴BE=2DC· .
21世纪教育网(www.21cnjy.com)
37.九年级数学(下)第28章《三角函数》单元检测卷
(考试范围:第28.2~第28章全章综合测试 解得参考时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1. cos60°的值是( )
A. B. C. D.
2. 在△ABC中,∠C=90°,∠A=30°,则的值是( )
A.1 B. 2 C. D.
在△ABC中,∠C=90°,cos A=0.6,AC=6,则AB的长是( )
A. 14 B. 12 C. 10 D. 8
如图,AC是电杆的一根拉线,测得BC=3米,∠ACB=60°,则AB的长为( )
A. 米 B. 8米 C. 6米 D. 2米
第4题图 第5题图 第6题图
如图,为了测量河岸A,B两点的距离,与在AB垂直的方向上取点C,测得AC=,∠ABC=,那么AB等于( )
A. B. C. D.
如图,先锋村准备在坡角为的山坡上栽树,要求相邻两树之间的水平距离为4米,那么这两树在坡面上的距离AB为( )
A. B. C. D.
如图,河堤横断面积迎水坡AB的坡比是1:,堤高BC=10m,则坡面AB的长度是( )
A. 15m B. 20m C. m D. 10m
第7题图 第8题图 第9题图
如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
A. m B. m C. m D. m
如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=2,则AB的长为( )
A. B. C. D.
如图,在四边形ABCD中,∠A=∠C=45°,∠ADB=∠ABC=105°,若AB+CD=,则AB的长为( )
A. B. C. 2 D.
二、填空题(每小题3分,共18分)
11. 如图,在△ABC中,∠C=90°,AC=5,BC=3,则tan B的值是 .
第11题图 第12题图 第14题图
12.如图,方格纸中的每个小方格都是边长为1个单位长度的的正方形,每个小正方形的顶点叫格点. △ABC的顶点都在方格的格点上,则cos A= .
在△ABC中,若,则∠C的度数是 .
如图,在△ABC中,AB为⊙O的直径,∠ABC=50°,∠C=70°,则tan∠ODB= .
如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,tan∠CAM=,则tan∠B的值为 .
第15题图 第16题图
如图,在正方形ABCD外作等腰Rt△CDE,DE=CE,连结AE,则cos∠AED= .
三、解答题(共8题,共72分)
17.(本题8分)计算:.
18.(本题8分)如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=5,解这个直角三角形.
(本题8分)如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求cos C的值.
20.(本题8分)在△ABC中,AD是BC边上的高,∠C=45°,sin B=,AD=1,求BC的长.
21.(本题8分)如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离为米,若在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响. 问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
(本题10分)如图,AB为⊙O的直径,=,过点C作⊙O的切线交AB的延长线于E,连接BC,CD,AD.
(1)求证:∠BCE=∠BAD;
(2)若,求cos∠CBA的值.
23.(本题10分)已知矩形ABCD中,E为BD上一点,EF⊥EC交AD于点F,FH⊥BD于点H.
(1)如图1,若AB=BC,猜想EH与CD的数量关系,并加以证明;
(2)如图2,若AB≠BC,敬爱喔ADB=,请探究EH与CD的数量关系.
24.(本题12分)在△ABC中,CA=CB,在△AED中,DA=DE,∠ACB=∠ADE,点D,E分别在CA,AB上.
(1)如图1,若∠ACB=90°,则CD与BE的数量关系是 ;
(2)若∠ACB=120°,将△AED绕点A旋转至如图2所示的位置,则CD与BE的数量关系是 ;
(3)若∠ACB=∠ADE=(0°<<90°),将△AED绕点A旋转至如图3所示的位置,探究线段CD与BE的数量关系,并予以证明.(用含的式子表示).
37.九年级数学(下)第28章《三角函数》单元检测卷
(考试范围:第28.2~第28章全章综合测试 解得参考时间:120分钟 满分120分)
一、选择题(每小题3分,共30分)
1. cos60°的值是( D )
A. B. C. D.
2. 在△ABC中,∠C=90°,∠A=30°,则的值是( C )
A.1 B. 2 C. D.
在△ABC中,∠C=90°,cos A=0.6,AC=6,则AB的长是( C )
A. 14 B. 12 C. 10 D. 8
如图,AC是电杆的一根拉线,测得BC=3米,∠ACB=60°,则AB的长为( A )
A. 米 B. 8米 C. 6米 D. 2米
第4题图 第5题图 第6题图
如图,为了测量河岸A,B两点的距离,与在AB垂直的方向上取点C,测得AC=,
∠ABC=,那么AB等于( C )
A. B. C. D.
如图,先锋村准备在坡角为的山坡上栽树,要求相邻两树之间的水平距离为4米,那
么这两树在坡面上的距离AB为( D )
A. B. C. D.
如图,河堤横断面积迎水坡AB的坡比是1:,堤高BC=10m,则坡面AB的长度是( B )
A. 15m B. 20m C. m D. 10m
第7题图 第8题图 第9题图
如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼
底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( A )
A. m B. m C. m D. m
如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=2,则AB的长为( C )
A. B. C. D.
如图,在四边形ABCD中,∠A=∠C=45°,∠ADB=∠ABC=105°,若AB+CD=,则AB的长为( B )
A. B. C. 2 D.
解:过D作DE⊥AB于E,过B作BF⊥CD于F,利用特殊角证明AB=CD.
二、填空题(每小题3分,共18分)
11. 如图,在△ABC中,∠C=90°,AC=5,BC=3,则tan B的值是 .
第11题图 第12题图 第14题图
12.如图,方格纸中的每个小方格都是边长为1个单位长度的的正方形,每个小正方形的顶点叫格点. △ABC的顶点都在方格的格点上,则cos A= .
在△ABC中,若,则∠C的度数是 60° .
如图,在△ABC中,AB为⊙O的直径,∠ABC=50°,∠C=70°,则tan∠ODB= .
如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,tan∠CAM=,则tan∠B的值为 .
第15题图 第16题图
如图,在正方形ABCD外作等腰Rt△CDE,DE=CE,连结AE,则cos∠AED= .
解:作AM⊥DE于M.
三、解答题(共8题,共72分)
17.(本题8分)计算:.
解:原式=.
18.(本题8分)如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=5,解这个直角三角形.
解:AB=10,BC=,∠A=60°.
(本题8分)如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求cos C的值.
解:∵在直角△ABD中,tan∠BAD=,
∴BD=AD · tan∠BAD=12×=9,
∴CD=BC-BD=14-9=5,
∴AC=,
∴.
20.(本题8分)在△ABC中,AD是BC边上的高,∠C=45°,sin B=,AD=1,求BC的长.
解:在Rt△ABD中,∵sin B=,
又∵AD=1,∴AB=3,
∵,
∴BD=,
在Rt△ADC中,∵∠C=45°,∴CD=AD=1,
∴BC=BD+DC=.
21.(本题8分)如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离为米,若在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响. 问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
解:过点C作CD⊥AB于D,∴BD=CD,AD=CD,
∵BD+AD=AB=(米),即,
∴CD=250,250米>200米.
答:在此路线段修建铁路,油库C不会受到影响.
(本题10分)如图,AB为⊙O的直径,=,过点C作⊙O的切线交AB的延长线于E,连接BC,CD,AD.
(1)求证:∠BCE=∠BAD;
(2)若,求cos∠CBA的值.
解:(1)连接AC,OC,∵=,∴∠BAC=∠DAC=∠OCA,
∵∠BCE+∠BCO=90°=∠OCA+∠BCO,∴∠BCE=∠OCA=∠BAD.
(2)延长BC,AD交于点F,∵∠BAC=∠DAC,∠BCA=90°,
∴AB=AF,BC=CF,设AB=AF=2R,
易证△CDF∽△ABF,∴,
设BC=CD=1,AD=2,
∴,∴R=(舍去负值),
∴AB=2R=,
∴cos∠CBA=.
23.(本题10分)已知矩形ABCD中,E为BD上一点,EF⊥EC交AD于点F,FH⊥BD于点H.
(1)如图1,若AB=BC,猜想EH与CD的数量关系,并加以证明;
(2)如图2,若AB≠BC,敬爱喔ADB=,请探究EH与CD的数量关系.
解:(1)EH=CD,作CG⊥BD于G,证△EHF≌△CGE.∴EH=CG=CD.
(2)作CG⊥BD于G,过E作MN⊥BC于N,交AD于M,易证△EHF∽△CGE
△EFM∽△CEN,∴ ①,∵ ②
①×②得,,∴EH=CD · sin.
24.(本题12分)在△ABC中,CA=CB,在△AED中,DA=DE,∠ACB=∠ADE,点D,E分别在CA,AB上.
(1)如图1,若∠ACB=90°,则CD与BE的数量关系是 ;
(2)若∠ACB=120°,将△AED绕点A旋转至如图2所示的位置,则CD与BE的数量关系是 ;
(3)若∠ACB=∠ADE=(0°<<90°),将△AED绕点A旋转至如图3所示的位置,探究线段CD与BE的数量关系,并予以证明.(用含的式子表示).
解:(1)BE=CD;
(2)BE=CD;
(3)BE=2CD · .
证明:如图,分别过点C、D作CM⊥AB于点M,DN⊥AE于点N,
∵CA=CB,DA=DE,∠ACB=∠ADE=,
∴∠CAB=∠DAE,∠ACM=∠ADN=,AM=AB,AN=AE,
∴∠CAD=∠BAE.
Rt△ACM和Rt△ADN中,sin∠ACM=,sin∠ADN=.
∴,又∠CAD=∠BAE. ∴△BAE∽△CAD,
∴,∴BE=2DC· .
21世纪教育网(www.21cnjy.com)
