39.人教版九年级中考模拟数学卷(含答案)
文档属性
| 名称 | 39.人教版九年级中考模拟数学卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 637.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 20:03:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
39.九年级数学中考模拟卷
(考试范围:综合测试 参考时间:120分钟 满分120分)
一、选择题(共10小题,每小题3分,共30分)
1、计算5-(-5)的结果为( )
A、10 B、0 C、-10 D、±10
2、若分式在实数范围内有意义,则实数的取值范围是( )
A、>-1 B、<-1 C、≠-1 D、=-1
3、下列运算中,正确的是( )
A、 B、 C、 D、
4、在一个不透明的盒子中有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放入盒中,通过大量重复摸球实验后发现摸到红球的频率稳定于0.4,由此可估计出盒中红球的个数约为( )
A、4 B、6 C、8 D、12
5、计算的结果为( )
A、-4 B、+4 C、-2+4 D、-4+4
6、点A(—3,2)关于原点对称的点的坐标为( )
A、(3,-2) B、(3,2) C、(-2,3) D、(2,-3)
7、如图是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,则这个几何体的左视图是( )
8、某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
劳动时间 3 3.5 4 4.5
人数 1 1 2 1
A、众数是2,平均数是3.8 B、中位数是4,平均数是3.8
C、众数是4,平均数是3.75 D、中位数是3.75,平均数是3.75
9、个数按一定的规律排列成1,-3,9,-27,81,-243,…。其中最后三个数的和为5103,则为( )
A、7 B、8 C、9 D、10
10、如图,在等腰直角三角形ABC中,AC=BC=,点P在以斜边AB为直径的半圆上,M为PC的中点,当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
A、 B、 C、 D、2
二、填空题(共6小题,每小题3分,共18分)
11、计算的结果为 .
12、计算的结果为 .
13、在一个不透明的袋中放有除颜色外完全相同的5个小球,其中3个红球,2个黄球,一次从中随机摸出两个球均为黄球的概率为 .
14、如图,把一张矩形纸片ABCD沿EF折叠,ED'交BC于G,若∠EFG=53°,则∠AEG的度数为 .
15、如图,在△ABC中,∠ABC=15°,∠ACB=37.5°,点D是BC边上的一点,且∠DAC=75°,则= .
16、已知实数满足,当0≤≤4时,实数能取整数值的个数是 个。
三、解答题(共8题,共72分)
17、(本小题8分)解方程组:
18、(本小题8分)如图,点B、E、C、F在同一条直线上,BE=CF,A=D,∠ABC=∠DEF。写出线段AC与DF之间的关系,并证明你的结论。
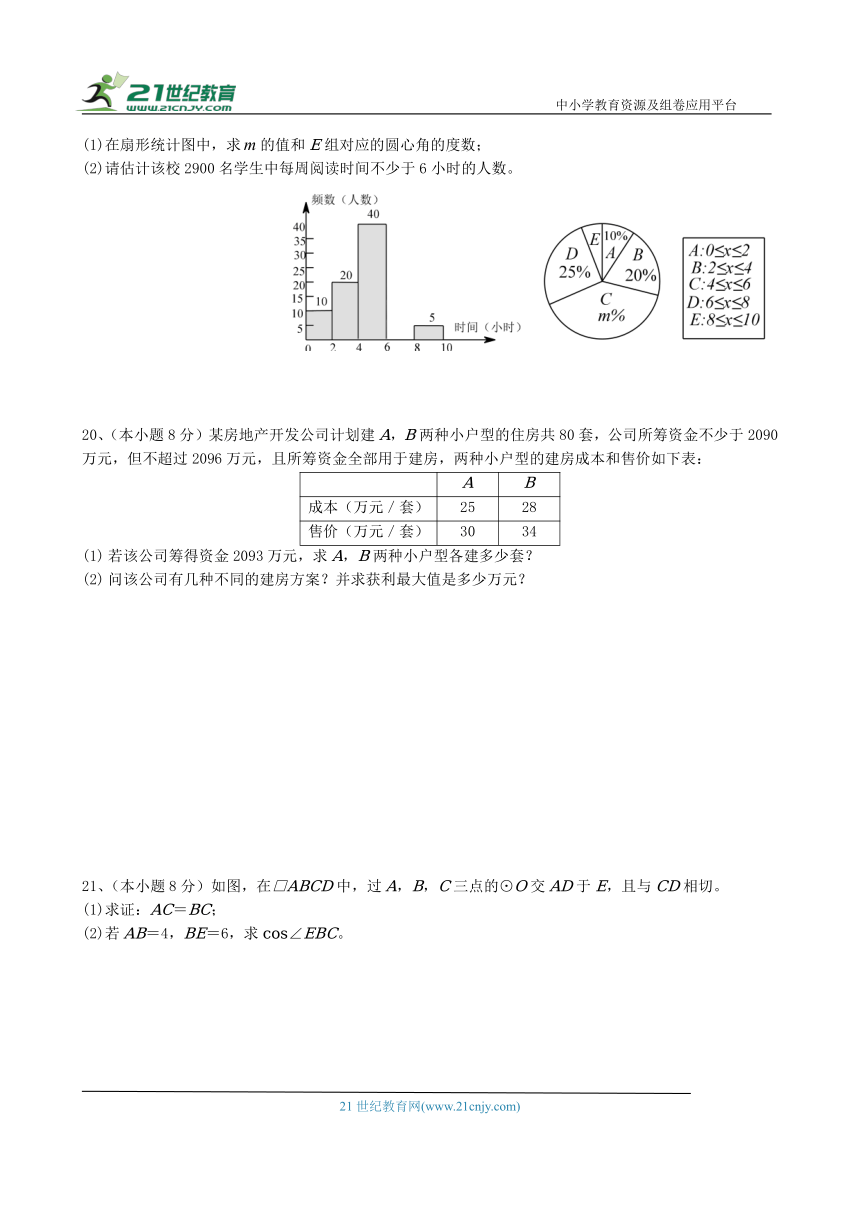
19、(本小题8分)某中学为了了解学生每周的课外阅读时间情况,随机抽查了部分学生,对学生每周的课外阅读时间(单位:小时)进行分组整理,并制成如图所示的不完整的频数分布直方图和扇形统计图。
(1)在扇形统计图中,求的值和E组对应的圆心角的度数;
(2)请估计该校2900名学生中每周阅读时间不少于6小时的人数。
20、(本小题8分)某房地产开发公司计划建A,B两种小户型的住房共80套,公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种小户型的建房成本和售价如下表:
A B
成本(万元/套) 25 28
售价(万元/套) 30 34
(1) 若该公司筹得资金2093万元,求A,B两种小户型各建多少套?
(2) 问该公司有几种不同的建房方案?并求获利最大值是多少万元?
21、(本小题8分)如图,在□ABCD中,过A,B,C三点的⊙O交AD于E,且与CD相切。
(1)求证:AC=BC;
(2)若AB=4,BE=6,求cos∠EBC。
22、(本小题10分)如图,双曲线(>0)与直线相交于A(2,),B(6,)两点。
(1)直接写出:关于的不等式>的解集是_____________,=________,=________;
(2)把点A绕平面内的某一点M顺时针旋转90°,恰好与点B重合,已知点M关于点A的对称点为M',求证:点M'在双曲线上;
(3)如图,点P是双曲线(>0)上的一个动点,PE⊥y轴于点E,过点P的直线:交轴的正半轴于点F,当点P向右运动时,四边形OEPF的面积S如何变化?给出你的结论并说明理由。
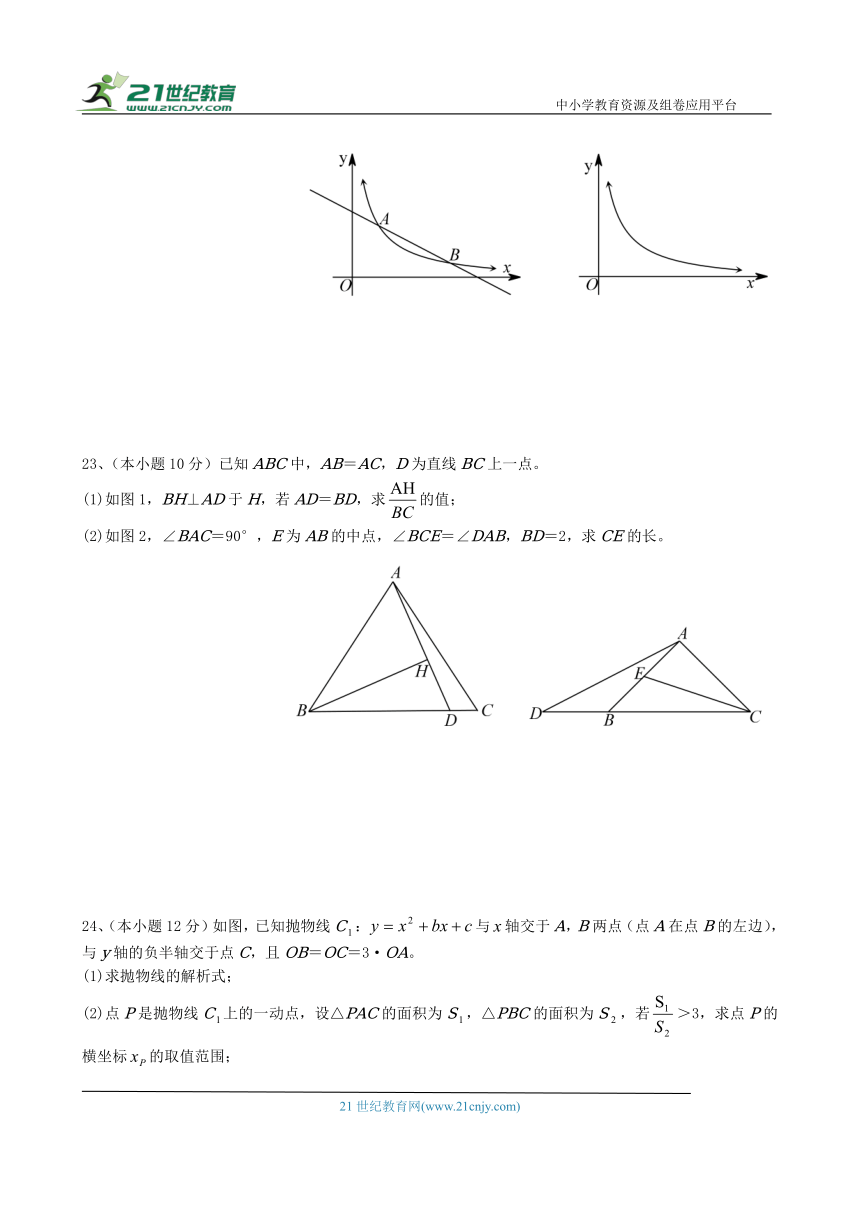
23、(本小题10分)已知ABC中,AB=AC,D为直线BC上一点。
(1)如图1,BH⊥AD于H,若AD=BD,求的值;
(2)如图2,∠BAC=90°,E为AB的中点,∠BCE=∠DAB,BD=2,求CE的长。
24、(本小题12分)如图,已知抛物线C:与轴交于A,B两点(点A在点B的左边),与y轴的负半轴交于点C,且OB=OC=3·OA。
(1)求抛物线的解析式;
(2)点P是抛物线C上的一动点,设△PAC的面积为S,△PBC的面积为S,若>3,求点P的横坐标的取值范围;
(3)把抛物线C向左平移1个单位长度,再向上平移4个单位长度得到抛物线C,点E(1-,2-8)到C上的某一点F的最小距离为,直接写出C上的点F的坐标及的值。
39.九年级数学中考模拟卷
(考试范围:综合测试 参考时间:120分钟 满分120分)
一、选择题(共10小题,每小题3分,共30分)
1、计算5-(-5)的结果为( A )
A、10 B、0 C、-10 D、±10
2、若分式在实数范围内有意义,则实数的取值范围是( C )
A、>-1 B、<-1 C、≠-1 D、=-1
3、下列运算中,正确的是( B )
A、 B、 C、 D、
4、在一个不透明的盒子中有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放入盒中,通过大量重复摸球实验后发现摸到红球的频率稳定于0.4,由此可估计出盒中红球的个数约为( C )
A、4 B、6 C、8 D、12
5、计算的结果为( D )
A、-4 B、+4 C、-2+4 D、-4+4
6、点A(—3,2)关于原点对称的点的坐标为( A )
A、(3,-2) B、(3,2) C、(-2,3) D、(2,-3)
7、如图是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,则这个几何体的左视图是( A )
8、某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是( B )
劳动时间 3 3.5 4 4.5
人数 1 1 2 1
A、众数是2,平均数是3.8 B、中位数是4,平均数是3.8
C、众数是4,平均数是3.75 D、中位数是3.75,平均数是3.75
9、个数按一定的规律排列成1,-3,9,-27,81,-243,…。其中最后三个数的和为5103,则为( C )
A、7 B、8 C、9 D、10
10、如图,在等腰直角三角形ABC中,AC=BC=,点P在以斜边AB为直径的半圆上,M为PC的中点,当点P沿半圆从点A运动至点B时,点M运动的路径长是( B )
A、 B、 C、 D、2
解:点M运动的路径是以△ABC的两直角边的中点连线为直径的半圆周,其路径长为半圆周长,设AC与BC的中点分别为点R,Q,易求RQ=2,则点M运动的路径为π
二、填空题(共6小题,每小题3分,共18分)
11、计算的结果为__4__。
12、计算的结果为___3__。
13、在一个不透明的袋中放有除颜色外完全相同的5个小球,其中3个红球,2个黄球,一次从中随机摸出两个球均为黄球的概率为___0.1____。
14、如图,把一张矩形纸片ABCD沿EF折叠,ED'交BC于G,若∠EFG=53°,则∠AEG的度数为_74°_。
15、如图,在△ABC中,∠ABC=15°,∠ACB=37.5°,点D是BC边上的一点,且∠DAC=75°,则=
16、已知实数满足,当0≤≤4时,实数能取整数值的个数是__7__个。
三、解答题(共8题,共72分)
17、(本小题8分)解方程组:
解:x=1,y=2
18、(本小题8分)如图,点B、E、C、F在同一条直线上,BE=CF,A=D,∠ABC=∠DEF。写出线段AC与DF之间的关系,并证明你的结论。
解:AC=DF且AC∥DF。
19、(本小题8分)某中学为了了解学生每周的课外阅读时间情况,随机抽查了部分学生,对学生每周的课外阅读时间(单位:小时)进行分组整理,并制成如图所示的不完整的频数分布直方图和扇形统计图。
(1)在扇形统计图中,求的值和E组对应的圆心角的度数;
(2)请估计该校2900名学生中每周阅读时间不少于6小时的人数。
解:(1)m=40,E组对应的圆心角的度数为18°;(2)2900×(25%+5%)=870(人)。
20、(本小题8分)某房地产开发公司计划建A,B两种小户型的住房共80套,公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种小户型的建房成本和售价如下表:
A B
成本(万元/套) 25 28
售价(万元/套) 30 34
(1) 若该公司筹得资金2093万元,求A,B两种小户型各建多少套?
(1) 问该公司有几种不同的建房方案?并求获利最大值是多少万元?
解:设A种小户型x套,则B种小户型(80-x)套。
(1)25x+28(80-x)=2093,解得:x=49,80-x=31,即A种小户型建49套,B种小户型建31套;
(2)依题意得:2090≤25x+28(80-x)≤2096,∴48≤x≤50,∴x可取48,49,50,故共有三种不同的方案。∵B种小户型获利最大,∴x=48时,获利最大,最大值为48×5+32×6=432(元)
21、(本小题8分)如图,在□ABCD中,过A,B,C三点的⊙O交AD于E,且与CD相切。
(1)求证:AC=BC;
(2)若AB=4,BE=6,求cos∠EBC。
解:(1)延长CO交AB于点F,
∵AB∥CD,CF⊥CD,∴CF⊥AB,∴AF=BF,∴AC=BC;
(2)连接AO,∵CF⊥AB,且AF=BF=2,∴AC=BC=AD,
∵AD∥BC,∴∠EAC=∠ACB,
∴弧CE=弧AB,∴弧AC=弧BE,∴AC=BE=6,∴CF=4,
设⊙O的半径为,则解得,OF=,
cos∠EBC=cos∠ACB=cos∠AOF==
22、(本小题10分)如图,双曲线(>0)与直线相交于A(2,),B(6,)两点。
(1)直接写出:关于的不等式>的解集是_____________,=________,=________;
(2)把点A绕平面内的某一点M顺时针旋转90°,恰好与点B重合,已知点M关于点A的对称点为M',求证:点M'在双曲线上;
(3)如图,点P是双曲线(>0)上的一个动点,PE⊥y轴于点E,过点P的直线:交轴的正半轴于点F,当点P向右运动时,四边形OEPF的面积S如何变化?给出你的结论并说明理由。
解:(1)0<x<2或x>6,k=6,b=4
(2)过点M作x轴的平行线,分别过点A,B作y轴的平行线,它们相交于点G,H(G在H点左边),△AGM≌△MHB,可设AG=MH=a,GM=BH=t,
∴,∴,M(3,0),∴M'(1,6),1×6=6=k,∴点M'在该双曲线上。
(3)过点P作PG⊥x轴于G,则S矩PEOG=S矩PEOG=6,△PFG∽△P1 F1 G1 ,∴=,
∵当向右平移时,PG<PG,∴S△PFG<S△PFG;
①当k>0时,S=6- S△PFG,S逐渐增大;②当k<0时,S=6+S△PFG,S逐渐减小。
23、(本小题10分)已知ABC中,AB=AC,D为直线BC上一点。
(1)如图1,BH⊥AD于H,若AD=BD,求的值;
(2)如图2,∠BAC=90°,E为AB的中点,∠BCE=∠DAB,BD=2,求CE的长。
解:(1)过A作AN⊥BC于点N,则BN=CN;
易证△ABN≌△BAH,∴AH=BN=CN,∴BC=2AH,∴=;
(2) ∠D+∠DAB=∠ABC=45°=∠ACE+∠BCE,∠D=∠ACE。
过B作BG⊥BD交AD于点G, ∴△DBG∽△CAE,∴==,
∵BD=2,∴BG=1,
∵∠ABG=∠EBC=45°,∠BCE=∠BAC,
∴△ABG∽△CBE,∴==,
∴BE=,∴AE=,AC=2,∴CE=。
24、(本小题12分)如图,已知抛物线C:与轴交于A,B两点(点A在点B的左边),与y轴的负半轴交于点C,且OB=OC=3·OA。
(1)求抛物线的解析式;
(2)点P是抛物线C上的一动点,设△PAC的面积为S,△PBC的面积为S,若>3,求点P的横坐标的取值范围;
(3)把抛物线C向左平移1个单位长度,再向上平移4个单位长度得到抛物线C,点E(1-,2-8)到C上的某一点F的最小距离为,直接写出C上的点F的坐标及的值。
解:(1);
(2)设当=3时的点P在抛物线上的P处,分别过A,B作直线PC的垂线,垂足分别为G,H,直线PC交x轴于M;
①当A,B分别在直线PC的异侧时,则===3,M(2,0),
直线PC:,联立:,=3.5;
②当A,B分别在直线PC的同侧时,同理可求M(5,0),直线PC:,
联立:,=2.6,∵>3,∴由图象可知:2.6<<3.5,且≠3.
(3) C的解析式为,点E在直线上运动,设F(,),
过F作FQ⊥y轴交直线于Q,则Q(,-2-6),∴FQ=+2+6,过F作FG垂直直线于G,则FG=FQ=+
∴F(-1,1),=。
21世纪教育网(www.21cnjy.com)
39.九年级数学中考模拟卷
(考试范围:综合测试 参考时间:120分钟 满分120分)
一、选择题(共10小题,每小题3分,共30分)
1、计算5-(-5)的结果为( )
A、10 B、0 C、-10 D、±10
2、若分式在实数范围内有意义,则实数的取值范围是( )
A、>-1 B、<-1 C、≠-1 D、=-1
3、下列运算中,正确的是( )
A、 B、 C、 D、
4、在一个不透明的盒子中有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放入盒中,通过大量重复摸球实验后发现摸到红球的频率稳定于0.4,由此可估计出盒中红球的个数约为( )
A、4 B、6 C、8 D、12
5、计算的结果为( )
A、-4 B、+4 C、-2+4 D、-4+4
6、点A(—3,2)关于原点对称的点的坐标为( )
A、(3,-2) B、(3,2) C、(-2,3) D、(2,-3)
7、如图是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,则这个几何体的左视图是( )
8、某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
劳动时间 3 3.5 4 4.5
人数 1 1 2 1
A、众数是2,平均数是3.8 B、中位数是4,平均数是3.8
C、众数是4,平均数是3.75 D、中位数是3.75,平均数是3.75
9、个数按一定的规律排列成1,-3,9,-27,81,-243,…。其中最后三个数的和为5103,则为( )
A、7 B、8 C、9 D、10
10、如图,在等腰直角三角形ABC中,AC=BC=,点P在以斜边AB为直径的半圆上,M为PC的中点,当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
A、 B、 C、 D、2
二、填空题(共6小题,每小题3分,共18分)
11、计算的结果为 .
12、计算的结果为 .
13、在一个不透明的袋中放有除颜色外完全相同的5个小球,其中3个红球,2个黄球,一次从中随机摸出两个球均为黄球的概率为 .
14、如图,把一张矩形纸片ABCD沿EF折叠,ED'交BC于G,若∠EFG=53°,则∠AEG的度数为 .
15、如图,在△ABC中,∠ABC=15°,∠ACB=37.5°,点D是BC边上的一点,且∠DAC=75°,则= .
16、已知实数满足,当0≤≤4时,实数能取整数值的个数是 个。
三、解答题(共8题,共72分)
17、(本小题8分)解方程组:
18、(本小题8分)如图,点B、E、C、F在同一条直线上,BE=CF,A=D,∠ABC=∠DEF。写出线段AC与DF之间的关系,并证明你的结论。
19、(本小题8分)某中学为了了解学生每周的课外阅读时间情况,随机抽查了部分学生,对学生每周的课外阅读时间(单位:小时)进行分组整理,并制成如图所示的不完整的频数分布直方图和扇形统计图。
(1)在扇形统计图中,求的值和E组对应的圆心角的度数;
(2)请估计该校2900名学生中每周阅读时间不少于6小时的人数。
20、(本小题8分)某房地产开发公司计划建A,B两种小户型的住房共80套,公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种小户型的建房成本和售价如下表:
A B
成本(万元/套) 25 28
售价(万元/套) 30 34
(1) 若该公司筹得资金2093万元,求A,B两种小户型各建多少套?
(2) 问该公司有几种不同的建房方案?并求获利最大值是多少万元?
21、(本小题8分)如图,在□ABCD中,过A,B,C三点的⊙O交AD于E,且与CD相切。
(1)求证:AC=BC;
(2)若AB=4,BE=6,求cos∠EBC。
22、(本小题10分)如图,双曲线(>0)与直线相交于A(2,),B(6,)两点。
(1)直接写出:关于的不等式>的解集是_____________,=________,=________;
(2)把点A绕平面内的某一点M顺时针旋转90°,恰好与点B重合,已知点M关于点A的对称点为M',求证:点M'在双曲线上;
(3)如图,点P是双曲线(>0)上的一个动点,PE⊥y轴于点E,过点P的直线:交轴的正半轴于点F,当点P向右运动时,四边形OEPF的面积S如何变化?给出你的结论并说明理由。
23、(本小题10分)已知ABC中,AB=AC,D为直线BC上一点。
(1)如图1,BH⊥AD于H,若AD=BD,求的值;
(2)如图2,∠BAC=90°,E为AB的中点,∠BCE=∠DAB,BD=2,求CE的长。
24、(本小题12分)如图,已知抛物线C:与轴交于A,B两点(点A在点B的左边),与y轴的负半轴交于点C,且OB=OC=3·OA。
(1)求抛物线的解析式;
(2)点P是抛物线C上的一动点,设△PAC的面积为S,△PBC的面积为S,若>3,求点P的横坐标的取值范围;
(3)把抛物线C向左平移1个单位长度,再向上平移4个单位长度得到抛物线C,点E(1-,2-8)到C上的某一点F的最小距离为,直接写出C上的点F的坐标及的值。
39.九年级数学中考模拟卷
(考试范围:综合测试 参考时间:120分钟 满分120分)
一、选择题(共10小题,每小题3分,共30分)
1、计算5-(-5)的结果为( A )
A、10 B、0 C、-10 D、±10
2、若分式在实数范围内有意义,则实数的取值范围是( C )
A、>-1 B、<-1 C、≠-1 D、=-1
3、下列运算中,正确的是( B )
A、 B、 C、 D、
4、在一个不透明的盒子中有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放入盒中,通过大量重复摸球实验后发现摸到红球的频率稳定于0.4,由此可估计出盒中红球的个数约为( C )
A、4 B、6 C、8 D、12
5、计算的结果为( D )
A、-4 B、+4 C、-2+4 D、-4+4
6、点A(—3,2)关于原点对称的点的坐标为( A )
A、(3,-2) B、(3,2) C、(-2,3) D、(2,-3)
7、如图是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,则这个几何体的左视图是( A )
8、某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是( B )
劳动时间 3 3.5 4 4.5
人数 1 1 2 1
A、众数是2,平均数是3.8 B、中位数是4,平均数是3.8
C、众数是4,平均数是3.75 D、中位数是3.75,平均数是3.75
9、个数按一定的规律排列成1,-3,9,-27,81,-243,…。其中最后三个数的和为5103,则为( C )
A、7 B、8 C、9 D、10
10、如图,在等腰直角三角形ABC中,AC=BC=,点P在以斜边AB为直径的半圆上,M为PC的中点,当点P沿半圆从点A运动至点B时,点M运动的路径长是( B )
A、 B、 C、 D、2
解:点M运动的路径是以△ABC的两直角边的中点连线为直径的半圆周,其路径长为半圆周长,设AC与BC的中点分别为点R,Q,易求RQ=2,则点M运动的路径为π
二、填空题(共6小题,每小题3分,共18分)
11、计算的结果为__4__。
12、计算的结果为___3__。
13、在一个不透明的袋中放有除颜色外完全相同的5个小球,其中3个红球,2个黄球,一次从中随机摸出两个球均为黄球的概率为___0.1____。
14、如图,把一张矩形纸片ABCD沿EF折叠,ED'交BC于G,若∠EFG=53°,则∠AEG的度数为_74°_。
15、如图,在△ABC中,∠ABC=15°,∠ACB=37.5°,点D是BC边上的一点,且∠DAC=75°,则=
16、已知实数满足,当0≤≤4时,实数能取整数值的个数是__7__个。
三、解答题(共8题,共72分)
17、(本小题8分)解方程组:
解:x=1,y=2
18、(本小题8分)如图,点B、E、C、F在同一条直线上,BE=CF,A=D,∠ABC=∠DEF。写出线段AC与DF之间的关系,并证明你的结论。
解:AC=DF且AC∥DF。
19、(本小题8分)某中学为了了解学生每周的课外阅读时间情况,随机抽查了部分学生,对学生每周的课外阅读时间(单位:小时)进行分组整理,并制成如图所示的不完整的频数分布直方图和扇形统计图。
(1)在扇形统计图中,求的值和E组对应的圆心角的度数;
(2)请估计该校2900名学生中每周阅读时间不少于6小时的人数。
解:(1)m=40,E组对应的圆心角的度数为18°;(2)2900×(25%+5%)=870(人)。
20、(本小题8分)某房地产开发公司计划建A,B两种小户型的住房共80套,公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种小户型的建房成本和售价如下表:
A B
成本(万元/套) 25 28
售价(万元/套) 30 34
(1) 若该公司筹得资金2093万元,求A,B两种小户型各建多少套?
(1) 问该公司有几种不同的建房方案?并求获利最大值是多少万元?
解:设A种小户型x套,则B种小户型(80-x)套。
(1)25x+28(80-x)=2093,解得:x=49,80-x=31,即A种小户型建49套,B种小户型建31套;
(2)依题意得:2090≤25x+28(80-x)≤2096,∴48≤x≤50,∴x可取48,49,50,故共有三种不同的方案。∵B种小户型获利最大,∴x=48时,获利最大,最大值为48×5+32×6=432(元)
21、(本小题8分)如图,在□ABCD中,过A,B,C三点的⊙O交AD于E,且与CD相切。
(1)求证:AC=BC;
(2)若AB=4,BE=6,求cos∠EBC。
解:(1)延长CO交AB于点F,
∵AB∥CD,CF⊥CD,∴CF⊥AB,∴AF=BF,∴AC=BC;
(2)连接AO,∵CF⊥AB,且AF=BF=2,∴AC=BC=AD,
∵AD∥BC,∴∠EAC=∠ACB,
∴弧CE=弧AB,∴弧AC=弧BE,∴AC=BE=6,∴CF=4,
设⊙O的半径为,则解得,OF=,
cos∠EBC=cos∠ACB=cos∠AOF==
22、(本小题10分)如图,双曲线(>0)与直线相交于A(2,),B(6,)两点。
(1)直接写出:关于的不等式>的解集是_____________,=________,=________;
(2)把点A绕平面内的某一点M顺时针旋转90°,恰好与点B重合,已知点M关于点A的对称点为M',求证:点M'在双曲线上;
(3)如图,点P是双曲线(>0)上的一个动点,PE⊥y轴于点E,过点P的直线:交轴的正半轴于点F,当点P向右运动时,四边形OEPF的面积S如何变化?给出你的结论并说明理由。
解:(1)0<x<2或x>6,k=6,b=4
(2)过点M作x轴的平行线,分别过点A,B作y轴的平行线,它们相交于点G,H(G在H点左边),△AGM≌△MHB,可设AG=MH=a,GM=BH=t,
∴,∴,M(3,0),∴M'(1,6),1×6=6=k,∴点M'在该双曲线上。
(3)过点P作PG⊥x轴于G,则S矩PEOG=S矩PEOG=6,△PFG∽△P1 F1 G1 ,∴=,
∵当向右平移时,PG<PG,∴S△PFG<S△PFG;
①当k>0时,S=6- S△PFG,S逐渐增大;②当k<0时,S=6+S△PFG,S逐渐减小。
23、(本小题10分)已知ABC中,AB=AC,D为直线BC上一点。
(1)如图1,BH⊥AD于H,若AD=BD,求的值;
(2)如图2,∠BAC=90°,E为AB的中点,∠BCE=∠DAB,BD=2,求CE的长。
解:(1)过A作AN⊥BC于点N,则BN=CN;
易证△ABN≌△BAH,∴AH=BN=CN,∴BC=2AH,∴=;
(2) ∠D+∠DAB=∠ABC=45°=∠ACE+∠BCE,∠D=∠ACE。
过B作BG⊥BD交AD于点G, ∴△DBG∽△CAE,∴==,
∵BD=2,∴BG=1,
∵∠ABG=∠EBC=45°,∠BCE=∠BAC,
∴△ABG∽△CBE,∴==,
∴BE=,∴AE=,AC=2,∴CE=。
24、(本小题12分)如图,已知抛物线C:与轴交于A,B两点(点A在点B的左边),与y轴的负半轴交于点C,且OB=OC=3·OA。
(1)求抛物线的解析式;
(2)点P是抛物线C上的一动点,设△PAC的面积为S,△PBC的面积为S,若>3,求点P的横坐标的取值范围;
(3)把抛物线C向左平移1个单位长度,再向上平移4个单位长度得到抛物线C,点E(1-,2-8)到C上的某一点F的最小距离为,直接写出C上的点F的坐标及的值。
解:(1);
(2)设当=3时的点P在抛物线上的P处,分别过A,B作直线PC的垂线,垂足分别为G,H,直线PC交x轴于M;
①当A,B分别在直线PC的异侧时,则===3,M(2,0),
直线PC:,联立:,=3.5;
②当A,B分别在直线PC的同侧时,同理可求M(5,0),直线PC:,
联立:,=2.6,∵>3,∴由图象可知:2.6<<3.5,且≠3.
(3) C的解析式为,点E在直线上运动,设F(,),
过F作FQ⊥y轴交直线于Q,则Q(,-2-6),∴FQ=+2+6,过F作FG垂直直线于G,则FG=FQ=+
∴F(-1,1),=。
21世纪教育网(www.21cnjy.com)
