《位置与方向(二)》(教案)-六年级数学上册人教版
文档属性
| 名称 | 《位置与方向(二)》(教案)-六年级数学上册人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 186.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 20:38:17 | ||
图片预览


文档简介
《位置与方向(二)》教学设计
教学内容:人教版小学数学六年级上册第 18 页例 1、第 19 页例 2。
教学目标:
1.能够根据方向和距离两个条件确定物体的位置,了解确定物体的方法,通过解决实际问题,让学生体会确定位置在生活中的应用。
2.学会通过测量描述物体在平面图上的具体位置,并会根据描述在平面图上画出物体的具体位置。
3.通过小组合作探讨,掌握画图方法。
4.培养学生空间观念和小组合作能力,体会数学知识与实际生活的紧密联系。
教学重点:
能够根据方向和距离两个条件确定物体的位置。
教学难点:
根据描述标出物体在平面图上的具体位置。教学准备:课件、学习单、实物展台;直尺、量角器(学生学具)。
教学设想:
1.教材分析及根据分析形成的设计思路:首先考虑前勾后连,本课为人教版小学数学六年级上册第二单元的内容,此前在三年级学生已经学过确定平面图形的八个方向:上北、下南、左西、右东、东北、东南、西北、西南,五年级还学过一种确定物体位置的方向:数对,所以本课从复习的角度,形成知识冲突,再通过丰富的学生活动,让学生自主发现确定物体位置的几个要素。
2.突破重难点的方法:先简单复习五年级的数对,使学生发现,数对不是确定位置的一般性方法,所以我们要寻找更一般的确定物体位置的方法,所以就想到了三年级学习的方向,但只有方向也不能唯一确定那一个点,所以我通过小组讨论的方法,形成知识冲突后进行自主探究。然后按“距离”“方向”“观测点”的顺序逐一攻破确定物体位置的条件。本课的层次感比较强,设计思路是层层递进的,有利于学生的理解。
3.结合实际:本课是《位置与方向》,非常贴合生活实际,借助形象的实例情景可以提升学生兴趣,丰富学生的生活经验。
教学过程:
一、师生谈话、复习导入
师:今天我们这节课学习什么?对,位置。其实在五年级我们已经学过描述物体位置的方法了,不知道大家还有没有印象,两个字。
生:数对。
师:这位同学他在班里的位置可以用数对(1,1)表示(指门口第一位的学生),那你的位置可以用数对多少来表示呢?(让学生思考一下,然后叫学生回答)
生:(2,2)。
师:判断?你能解释一下是什么意思吗?
师:他有些遗忘了,谁来帮帮他?
生:他在第 2 列第 2 行,所以是数对(2,2)。
师:谁还想说一下自己的位置?
师:在教室里,我们可以用数对帮助我们确定位置,但随着年级升高,我们观察世界的角度和视野就会发生变化。想象一下,当我们来到了辽阔的草原,广阔的天空,浩瀚的宇宙,这时候一些物体要确定位置,我们该怎么办呢?这就是我们今天学习的内容。(板书:确定位置)
【设计意图】
回顾旧知,贴合新课标强调的知识的一致性,有利于学生系统的掌握知识。在这里也让学生形成只是冲突,更好的引导学生思考问题。
二、新授(物资短缺,驰援 A 市)
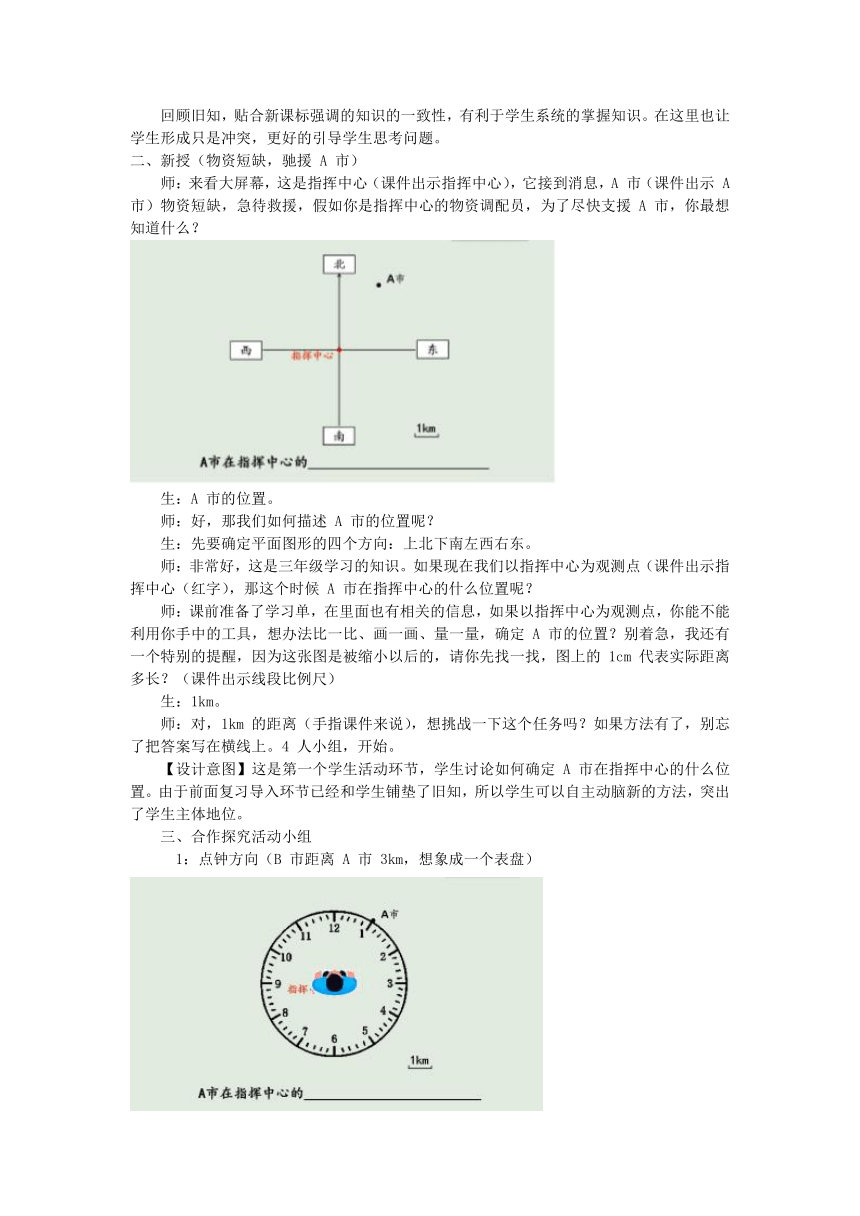
师:来看大屏幕,这是指挥中心(课件出示指挥中心),它接到消息,A 市(课件出示 A 市)物资短缺,急待救援,假如你是指挥中心的物资调配员,为了尽快支援 A 市,你最想知道什么?
生:A 市的位置。
师:好,那我们如何描述 A 市的位置呢?
生:先要确定平面图形的四个方向:上北下南左西右东。
师:非常好,这是三年级学习的知识。如果现在我们以指挥中心为观测点(课件出示指挥中心(红字),那这个时候 A 市在指挥中心的什么位置呢?
师:课前准备了学习单,在里面也有相关的信息,如果以指挥中心为观测点,你能不能利用你手中的工具,想办法比一比、画一画、量一量,确定 A 市的位置?别着急,我还有一个特别的提醒,因为这张图是被缩小以后的,请你先找一找,图上的 1cm 代表实际距离多长?(课件出示线段比例尺)
生:1km。
师:对,1km 的距离(手指课件来说),想挑战一下这个任务吗?如果方法有了,别忘了把答案写在横线上。4 人小组,开始。
【设计意图】这是第一个学生活动环节,学生讨论如何确定 A 市在指挥中心的什么位置。由于前面复习导入环节已经和学生铺垫了旧知,所以学生可以自主动脑新的方法,突出了学生主体地位。
三、合作探究活动小组
1:点钟方向(B 市距离 A 市 3km,想象成一个表盘)
生:我把它想象成一个表盘,自己站在表盘的中心,那 A 市大约就在指挥中心的1 点钟方向。
师:同学们听明白了吗?他用了一个非常特别的工具,表盘。老师这里也准备了一个表盘(课件出示表盘和人物顶视图)这种表示方法叫做点钟方向,就是以站立点为中心,观察者的正前方定为 12 点,那么 A 市大约就在观察者的 1 点钟方向。
你的知识可真丰富,还有哪个小组有自己的想法?
【设计意图】这里是我的一个创新,但由于教材上没有,所以只是想拓宽学生思路,扩大知识面。但课前我也做过学情调查,有 80%以上的学生是明白什么是点钟方向的,所以这里的预设学生是可以理解的。但由于时间有限,预设这个知识点讲清楚后不太方便做练习。
小组 2:“东北方向 30°3km 处”
生:首先我们先确定 A 市在指挥中心的东北方向,把 A 市和指挥中心连接起来,用量角器发现这个夹角是 30°,然后因为图上的 1cm 表示实际的 1km,这一段是3cm,所以就是 3km,所以我们小组发现 A 市在指挥中心的东北方向 30°3km 处。
师:可以吗?这个小组汇报的结果有一个 3km,我想问问同学们,你在小组讨论的时候去量了吗?你是怎么量的呢?谁来上来量一量,3km 你是怎么量的?
(生上台演示)
生:先要把尺子上的 0 刻度线对准指挥中心,按照我们连接的这条线,看到 A 市的点是对准了 3cm,所以量出来是 3cm。
师:同意吗?我想问问同学们,为什么非要量出距离呢?要是没有距离行不行?
生:如果没有距离的话,他就是一条射线,射线是无限长的,所以这样怎样也找不到它。
师:你听明白了吗?看来这个 3km 是必须要有的,所以量出距离很重要。(板书:3km 处)
师:再来看,前面他写的“东北方向 30°”,你同意吗?
生:会有些偏差,不应该是东北方向,因为不知道到底是偏北还是偏东。
师:也就是说如果单独说东北 30°的话,有几个东北 30°?
生:有两个。
师:你能上来画画有哪两个吗?(生带着自己的铅笔、直尺、量角器上台演示)
生:首先是北偏东 30°,把 0 刻度线对准北,看 A 市和指挥中心的连线正好和 30°重合。还有一个是东偏北 30°,把 0 刻度线对准东,所以此时 30°应该在这。
【设计意图】这里设计的问题是串联的,有层次性,讲解的是教材上明确的知识点,预设这个地方尽量找学生把所有可能出错的点展示出来,这样 60°就可以不用再细讲了。
师:你同意吗?非常好。我刚刚还看见有同学写 60°的,哪个小组写的答案是60°?(小组 3 上台演示)
小组 3:“东偏北 60°方向 3km 处”(生带着自己的量角器上台演示他的 60°是怎么画的)
生:首先把 0 刻度线对准东,它是东偏北,看到 A 市是在 60°,所以是东偏北60°。
师:你看明白了吗?那为什么有一个 30°有一个 60°呢?我们来看看这两幅图的区别。区别在哪?
(生上台,边指着边说)
生:每次量角器的 0 刻度线对准的方位不同,左边是对准的北,右边是对准的东。
师:听明白了吗?谁能再来说一说,到底区别在哪?
生:每次量角器的 0 刻度线对准的方位不同,左边是对准的北,右边是对准的东。
师:好,伸出你的手,我们一起来指一指左边的这幅图,0 刻度线是从哪个方向开始的?
(生:北)然后偏?
(生:东)右边这幅图是以
(生:东)作为 0 刻度线,作为起点,然后往
(生:北)去偏。
师:像这样的,左边的图,在数学上叫做什么?
生:北偏东 30°
师:也就是开始我们的 0 刻度线冲的是?
(生:北)好,也就是说是以北为基准。(板书:基准)
师:右边这幅图呢?叫做什么?
生:东偏北 60°
师:这次是以谁为基准?
(生:东)
师:我还看到一个小组,写的是比书上还要标准的答案。
(出示小组 4 的答案:北偏东 30°距离指挥中心 3km 处)
师:你看这个同学还写了“距离指挥中心”,为什么要强调在指挥中心呢?
生:因为是以指挥中心为观测点来测量的。
师:非常好,也就是说我们的前提条件是非常重要的
(板书:A 市在指挥中心的),这里的指挥中心是观测点(板书:画出指挥中心四个字,写上“观测点”)。
师:这两种说法都是合理的。同位两个再来说一说 A 市到底在指挥中心的什么位置?(同位两人相互说)
师:所以我们知道了,A 市在指挥中心的北偏东 30°或者东偏北 60°方向 3km处。其中,这个 3km 叫做什么?
(生:距离)很好(板书:距离),中间的呢?叫做什么?
(生:方向)
具体来说,除了方向,还有角度
(板书:方向、角度)
今天我们学习的内容,就是用角度、方向和距离来确定位置。
【设计意图】这里预设在 A 市的两种位置表示方法都出来以后,接着进行总结(观测点、以谁为基准、角度、方向、距离),为下面的练习做准备。
四、跟进练习,总结提升
师:A 市的位置我们已经找到了,可以去运送物资了,但哪些城市方便支援 A 市呢?工作人员找到了三个城市,他们在哪呢?先来看前两个城市,B 市和 C 市,如果仍然以指挥中心作为观测点,它们的位置该怎么来描述呢?30 秒,自己先小声说一说。
生:B 市在指挥中心的南偏东方向 50°,距离指挥中心 2km。
师:判断?其他的说法有吗?
生:B 市在指挥中心的东偏南 40°,距离指挥中心 2km。
师:判断?师再表扬:你注意到了吗?这两个同学听讲很认真,都把观测点说出来了。
(课件出示 B 市的两种说法)
师:谁再来说 C 市的位置?
生:C 市在指挥中心的西偏北 25°方向 4km 处。
师:判断?其他的说法有吗?
生:C 市在北偏西 65°方向 4km 处。
师:听出来了吗?少了什么?
生:没加观测点,应该是 C 市在指挥中心的北偏西 65°方向 4km 处。
师;同意吗?倾听是多么的重要。谁再来说?
生:C 市在指挥中心的北偏西 65°方向 4km 处。
师:这个 65°怎么来的?图上没有啊?
生:因为 90-25=65。
师:也就是说我们有时也需要计算,算出北偏西的度数。
【设计意图】预设先出两个简单的练习,让学生直接说出每个城市两种表示的方法。进而和下面的逐步出示 D 市的线索形成对比,巩固知识点。
师:非常好,B 市和 C 市都找到了,还有一个 D 市,D 市我不直接给你,但我给你线索,你看看你能找到它吗?
(课件出示: D 市在指挥中心的南偏西方向)
师:能找到吗?没有?有没有大概位置?
(生上台指)
生:在南偏西的区域。
师:判断?在南偏西这片区域,非常好。
【设计意图】思路是逐步缩小范围,面——线——点,逐步递进。
师:再来,又给你条件了。找到了吗?在哪?
(生上台,在大屏幕前指一下)
生:他是在南偏西 45°的射线上。
(课件出示 D 市在指挥中心的南偏西 45°方向)
师:其他同学,拿出你的手指指,在什么位置?有同学画了一条(出示南偏西射线),非常好。
师:再来,现在还缺什么?
(生:距离)
好,都伸出你的小手来,大家来目测一下5km 在哪?
(出示 5km 的位置)
你指的对不对?
(生:对)
师:好,BCD 三个城市,你觉得哪个最难找?
(生:D 市)
对,D 市,为什么呢?首先给你的第一个线索是什么?
(生:南偏西方向)
它是一个什么?一字。
(生:是一个面)
师:真棒,又给了你?
(生:线)
师:最后是?
(生:点)
师:真棒,我们今天研究的确定位置,就是这样,由面,到线,再到点,逐渐精确的研究的方法。
五、小结提升
师:到这里,老师还有几个小问题想问问大家。
(出示学习单上的图)
刚才说,用角度、方向和距离来确定位置,假如只告诉你“北偏东 30°”,这是什么?
(生:射线)如果只告诉你距离,只告诉你 3km,画出来是个什么?
(生:是一个圆)非常棒,当我这几个条件都告诉你,就形成了一个点了。
师:同学们,让我们来回忆一下:在一年级,我们用上、下、左、右、前、后,来确定物体的相对位置;到了三年级,我们又认识了这 8 个方向;五年级,我们学习了第一种确定平面上物体位置的方法:数对;再到今天,我们又学习了用角度、方向和距离这种更加精确、更加普遍的确定物体位置的方法。其中这就是二维空间(手指着课件中六年级的),我们需要角度、方向和距离才能确定物体的准确位置。你猜猜,如果是三维空间,需要几个条件?
(生:三个)这部分内容我们放到中学阶段再来研究。
【设计意图】这里的设计是为了总结提升,从今天学面上确定物体位置,延伸到数学上的二维空间,以至于中学阶段的三维空间,使学生形成初步的空间概念,开拓学生思维。
师:这节课我们就上到这里,下课。
板书设计:
教学内容:人教版小学数学六年级上册第 18 页例 1、第 19 页例 2。
教学目标:
1.能够根据方向和距离两个条件确定物体的位置,了解确定物体的方法,通过解决实际问题,让学生体会确定位置在生活中的应用。
2.学会通过测量描述物体在平面图上的具体位置,并会根据描述在平面图上画出物体的具体位置。
3.通过小组合作探讨,掌握画图方法。
4.培养学生空间观念和小组合作能力,体会数学知识与实际生活的紧密联系。
教学重点:
能够根据方向和距离两个条件确定物体的位置。
教学难点:
根据描述标出物体在平面图上的具体位置。教学准备:课件、学习单、实物展台;直尺、量角器(学生学具)。
教学设想:
1.教材分析及根据分析形成的设计思路:首先考虑前勾后连,本课为人教版小学数学六年级上册第二单元的内容,此前在三年级学生已经学过确定平面图形的八个方向:上北、下南、左西、右东、东北、东南、西北、西南,五年级还学过一种确定物体位置的方向:数对,所以本课从复习的角度,形成知识冲突,再通过丰富的学生活动,让学生自主发现确定物体位置的几个要素。
2.突破重难点的方法:先简单复习五年级的数对,使学生发现,数对不是确定位置的一般性方法,所以我们要寻找更一般的确定物体位置的方法,所以就想到了三年级学习的方向,但只有方向也不能唯一确定那一个点,所以我通过小组讨论的方法,形成知识冲突后进行自主探究。然后按“距离”“方向”“观测点”的顺序逐一攻破确定物体位置的条件。本课的层次感比较强,设计思路是层层递进的,有利于学生的理解。
3.结合实际:本课是《位置与方向》,非常贴合生活实际,借助形象的实例情景可以提升学生兴趣,丰富学生的生活经验。
教学过程:
一、师生谈话、复习导入
师:今天我们这节课学习什么?对,位置。其实在五年级我们已经学过描述物体位置的方法了,不知道大家还有没有印象,两个字。
生:数对。
师:这位同学他在班里的位置可以用数对(1,1)表示(指门口第一位的学生),那你的位置可以用数对多少来表示呢?(让学生思考一下,然后叫学生回答)
生:(2,2)。
师:判断?你能解释一下是什么意思吗?
师:他有些遗忘了,谁来帮帮他?
生:他在第 2 列第 2 行,所以是数对(2,2)。
师:谁还想说一下自己的位置?
师:在教室里,我们可以用数对帮助我们确定位置,但随着年级升高,我们观察世界的角度和视野就会发生变化。想象一下,当我们来到了辽阔的草原,广阔的天空,浩瀚的宇宙,这时候一些物体要确定位置,我们该怎么办呢?这就是我们今天学习的内容。(板书:确定位置)
【设计意图】
回顾旧知,贴合新课标强调的知识的一致性,有利于学生系统的掌握知识。在这里也让学生形成只是冲突,更好的引导学生思考问题。
二、新授(物资短缺,驰援 A 市)
师:来看大屏幕,这是指挥中心(课件出示指挥中心),它接到消息,A 市(课件出示 A 市)物资短缺,急待救援,假如你是指挥中心的物资调配员,为了尽快支援 A 市,你最想知道什么?
生:A 市的位置。
师:好,那我们如何描述 A 市的位置呢?
生:先要确定平面图形的四个方向:上北下南左西右东。
师:非常好,这是三年级学习的知识。如果现在我们以指挥中心为观测点(课件出示指挥中心(红字),那这个时候 A 市在指挥中心的什么位置呢?
师:课前准备了学习单,在里面也有相关的信息,如果以指挥中心为观测点,你能不能利用你手中的工具,想办法比一比、画一画、量一量,确定 A 市的位置?别着急,我还有一个特别的提醒,因为这张图是被缩小以后的,请你先找一找,图上的 1cm 代表实际距离多长?(课件出示线段比例尺)
生:1km。
师:对,1km 的距离(手指课件来说),想挑战一下这个任务吗?如果方法有了,别忘了把答案写在横线上。4 人小组,开始。
【设计意图】这是第一个学生活动环节,学生讨论如何确定 A 市在指挥中心的什么位置。由于前面复习导入环节已经和学生铺垫了旧知,所以学生可以自主动脑新的方法,突出了学生主体地位。
三、合作探究活动小组
1:点钟方向(B 市距离 A 市 3km,想象成一个表盘)
生:我把它想象成一个表盘,自己站在表盘的中心,那 A 市大约就在指挥中心的1 点钟方向。
师:同学们听明白了吗?他用了一个非常特别的工具,表盘。老师这里也准备了一个表盘(课件出示表盘和人物顶视图)这种表示方法叫做点钟方向,就是以站立点为中心,观察者的正前方定为 12 点,那么 A 市大约就在观察者的 1 点钟方向。
你的知识可真丰富,还有哪个小组有自己的想法?
【设计意图】这里是我的一个创新,但由于教材上没有,所以只是想拓宽学生思路,扩大知识面。但课前我也做过学情调查,有 80%以上的学生是明白什么是点钟方向的,所以这里的预设学生是可以理解的。但由于时间有限,预设这个知识点讲清楚后不太方便做练习。
小组 2:“东北方向 30°3km 处”
生:首先我们先确定 A 市在指挥中心的东北方向,把 A 市和指挥中心连接起来,用量角器发现这个夹角是 30°,然后因为图上的 1cm 表示实际的 1km,这一段是3cm,所以就是 3km,所以我们小组发现 A 市在指挥中心的东北方向 30°3km 处。
师:可以吗?这个小组汇报的结果有一个 3km,我想问问同学们,你在小组讨论的时候去量了吗?你是怎么量的呢?谁来上来量一量,3km 你是怎么量的?
(生上台演示)
生:先要把尺子上的 0 刻度线对准指挥中心,按照我们连接的这条线,看到 A 市的点是对准了 3cm,所以量出来是 3cm。
师:同意吗?我想问问同学们,为什么非要量出距离呢?要是没有距离行不行?
生:如果没有距离的话,他就是一条射线,射线是无限长的,所以这样怎样也找不到它。
师:你听明白了吗?看来这个 3km 是必须要有的,所以量出距离很重要。(板书:3km 处)
师:再来看,前面他写的“东北方向 30°”,你同意吗?
生:会有些偏差,不应该是东北方向,因为不知道到底是偏北还是偏东。
师:也就是说如果单独说东北 30°的话,有几个东北 30°?
生:有两个。
师:你能上来画画有哪两个吗?(生带着自己的铅笔、直尺、量角器上台演示)
生:首先是北偏东 30°,把 0 刻度线对准北,看 A 市和指挥中心的连线正好和 30°重合。还有一个是东偏北 30°,把 0 刻度线对准东,所以此时 30°应该在这。
【设计意图】这里设计的问题是串联的,有层次性,讲解的是教材上明确的知识点,预设这个地方尽量找学生把所有可能出错的点展示出来,这样 60°就可以不用再细讲了。
师:你同意吗?非常好。我刚刚还看见有同学写 60°的,哪个小组写的答案是60°?(小组 3 上台演示)
小组 3:“东偏北 60°方向 3km 处”(生带着自己的量角器上台演示他的 60°是怎么画的)
生:首先把 0 刻度线对准东,它是东偏北,看到 A 市是在 60°,所以是东偏北60°。
师:你看明白了吗?那为什么有一个 30°有一个 60°呢?我们来看看这两幅图的区别。区别在哪?
(生上台,边指着边说)
生:每次量角器的 0 刻度线对准的方位不同,左边是对准的北,右边是对准的东。
师:听明白了吗?谁能再来说一说,到底区别在哪?
生:每次量角器的 0 刻度线对准的方位不同,左边是对准的北,右边是对准的东。
师:好,伸出你的手,我们一起来指一指左边的这幅图,0 刻度线是从哪个方向开始的?
(生:北)然后偏?
(生:东)右边这幅图是以
(生:东)作为 0 刻度线,作为起点,然后往
(生:北)去偏。
师:像这样的,左边的图,在数学上叫做什么?
生:北偏东 30°
师:也就是开始我们的 0 刻度线冲的是?
(生:北)好,也就是说是以北为基准。(板书:基准)
师:右边这幅图呢?叫做什么?
生:东偏北 60°
师:这次是以谁为基准?
(生:东)
师:我还看到一个小组,写的是比书上还要标准的答案。
(出示小组 4 的答案:北偏东 30°距离指挥中心 3km 处)
师:你看这个同学还写了“距离指挥中心”,为什么要强调在指挥中心呢?
生:因为是以指挥中心为观测点来测量的。
师:非常好,也就是说我们的前提条件是非常重要的
(板书:A 市在指挥中心的),这里的指挥中心是观测点(板书:画出指挥中心四个字,写上“观测点”)。
师:这两种说法都是合理的。同位两个再来说一说 A 市到底在指挥中心的什么位置?(同位两人相互说)
师:所以我们知道了,A 市在指挥中心的北偏东 30°或者东偏北 60°方向 3km处。其中,这个 3km 叫做什么?
(生:距离)很好(板书:距离),中间的呢?叫做什么?
(生:方向)
具体来说,除了方向,还有角度
(板书:方向、角度)
今天我们学习的内容,就是用角度、方向和距离来确定位置。
【设计意图】这里预设在 A 市的两种位置表示方法都出来以后,接着进行总结(观测点、以谁为基准、角度、方向、距离),为下面的练习做准备。
四、跟进练习,总结提升
师:A 市的位置我们已经找到了,可以去运送物资了,但哪些城市方便支援 A 市呢?工作人员找到了三个城市,他们在哪呢?先来看前两个城市,B 市和 C 市,如果仍然以指挥中心作为观测点,它们的位置该怎么来描述呢?30 秒,自己先小声说一说。
生:B 市在指挥中心的南偏东方向 50°,距离指挥中心 2km。
师:判断?其他的说法有吗?
生:B 市在指挥中心的东偏南 40°,距离指挥中心 2km。
师:判断?师再表扬:你注意到了吗?这两个同学听讲很认真,都把观测点说出来了。
(课件出示 B 市的两种说法)
师:谁再来说 C 市的位置?
生:C 市在指挥中心的西偏北 25°方向 4km 处。
师:判断?其他的说法有吗?
生:C 市在北偏西 65°方向 4km 处。
师:听出来了吗?少了什么?
生:没加观测点,应该是 C 市在指挥中心的北偏西 65°方向 4km 处。
师;同意吗?倾听是多么的重要。谁再来说?
生:C 市在指挥中心的北偏西 65°方向 4km 处。
师:这个 65°怎么来的?图上没有啊?
生:因为 90-25=65。
师:也就是说我们有时也需要计算,算出北偏西的度数。
【设计意图】预设先出两个简单的练习,让学生直接说出每个城市两种表示的方法。进而和下面的逐步出示 D 市的线索形成对比,巩固知识点。
师:非常好,B 市和 C 市都找到了,还有一个 D 市,D 市我不直接给你,但我给你线索,你看看你能找到它吗?
(课件出示: D 市在指挥中心的南偏西方向)
师:能找到吗?没有?有没有大概位置?
(生上台指)
生:在南偏西的区域。
师:判断?在南偏西这片区域,非常好。
【设计意图】思路是逐步缩小范围,面——线——点,逐步递进。
师:再来,又给你条件了。找到了吗?在哪?
(生上台,在大屏幕前指一下)
生:他是在南偏西 45°的射线上。
(课件出示 D 市在指挥中心的南偏西 45°方向)
师:其他同学,拿出你的手指指,在什么位置?有同学画了一条(出示南偏西射线),非常好。
师:再来,现在还缺什么?
(生:距离)
好,都伸出你的小手来,大家来目测一下5km 在哪?
(出示 5km 的位置)
你指的对不对?
(生:对)
师:好,BCD 三个城市,你觉得哪个最难找?
(生:D 市)
对,D 市,为什么呢?首先给你的第一个线索是什么?
(生:南偏西方向)
它是一个什么?一字。
(生:是一个面)
师:真棒,又给了你?
(生:线)
师:最后是?
(生:点)
师:真棒,我们今天研究的确定位置,就是这样,由面,到线,再到点,逐渐精确的研究的方法。
五、小结提升
师:到这里,老师还有几个小问题想问问大家。
(出示学习单上的图)
刚才说,用角度、方向和距离来确定位置,假如只告诉你“北偏东 30°”,这是什么?
(生:射线)如果只告诉你距离,只告诉你 3km,画出来是个什么?
(生:是一个圆)非常棒,当我这几个条件都告诉你,就形成了一个点了。
师:同学们,让我们来回忆一下:在一年级,我们用上、下、左、右、前、后,来确定物体的相对位置;到了三年级,我们又认识了这 8 个方向;五年级,我们学习了第一种确定平面上物体位置的方法:数对;再到今天,我们又学习了用角度、方向和距离这种更加精确、更加普遍的确定物体位置的方法。其中这就是二维空间(手指着课件中六年级的),我们需要角度、方向和距离才能确定物体的准确位置。你猜猜,如果是三维空间,需要几个条件?
(生:三个)这部分内容我们放到中学阶段再来研究。
【设计意图】这里的设计是为了总结提升,从今天学面上确定物体位置,延伸到数学上的二维空间,以至于中学阶段的三维空间,使学生形成初步的空间概念,开拓学生思维。
师:这节课我们就上到这里,下课。
板书设计:
