26.2 实际问题与反比例函数一课一练(含解析)
文档属性
| 名称 | 26.2 实际问题与反比例函数一课一练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 755.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 22:59:36 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
26.2 实际问题与反比例函数一课一练
一、单选题
1.一个圆柱的侧面展开图是一个面积为4的矩形,这个圆柱的母线l与圆柱的底面半径r之间的函数关系是( )
A.正比例函数 B.反比例函数 C.一次函数 D.二次函数
2.某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为2公顷,则总人口有100人
D.当该村总人口为50人时,人均耕地面积为1公顷
3.研究发现,近视镜的度数y(度)与镜片焦距x(米)成反比例函数关系,小明佩戴的400度近视镜片的焦距为0.25米,经过一段时间的矫正治疗加之注意用眼健康,现在镜片焦距为0.4米,则小明的近视镜度数可以调整为( )
A.300度 B.500度 C.250度 D.200度
4.已知蓄电池的电压为定值.使用电池时,电流I(A)与电阻R(Ω)是反比例函数关系,图象如图所示.如果以此蓄电池为电源的电器的限制电流不能超过3A,那么电器的可变电阻R(Ω)应控制在( )
A.R≥1 B.0<R≤2 C.R≥2 D.0<R≤1
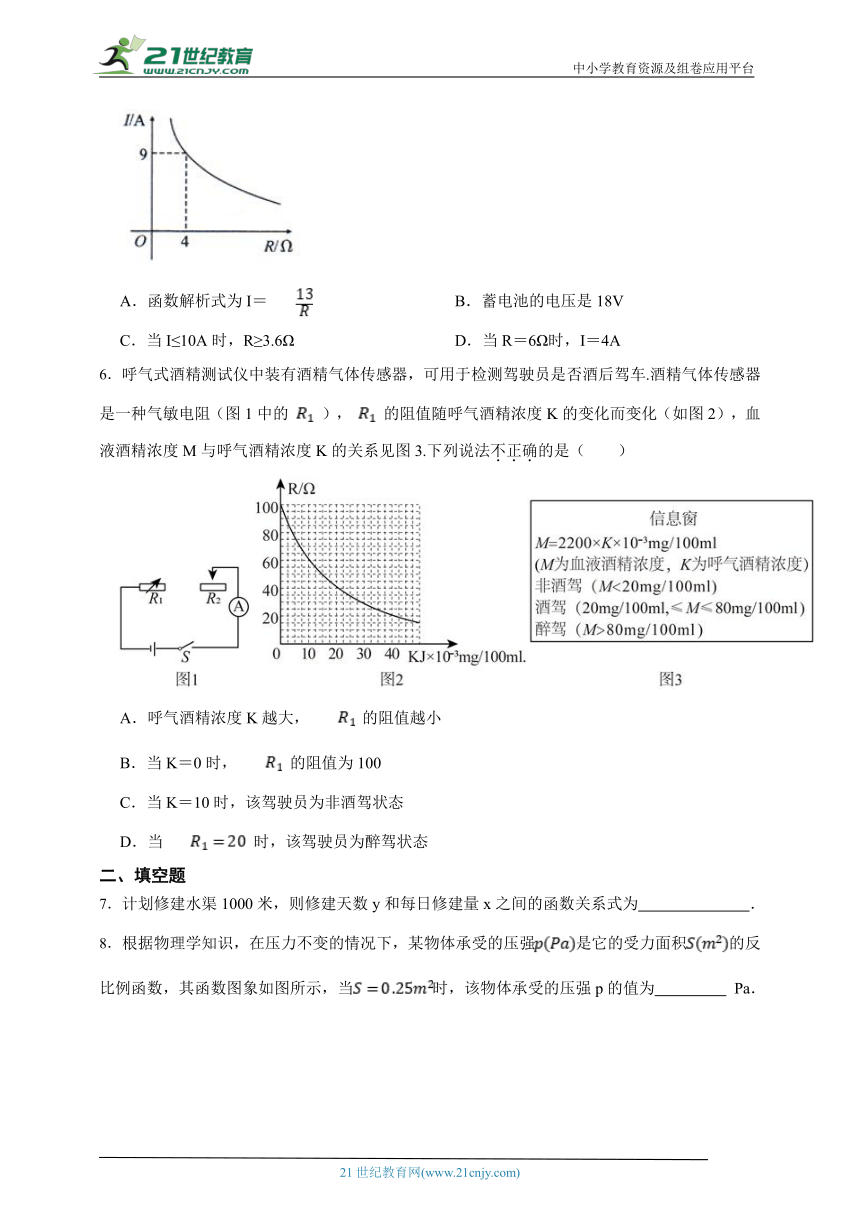
5.已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为I= B.蓄电池的电压是18V
C.当I≤10A时,R≥3.6Ω D.当R=6Ω时,I=4A
6.呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的 ), 的阻值随呼气酒精浓度K的变化而变化(如图2),血液酒精浓度M与呼气酒精浓度K的关系见图3.下列说法不正确的是( )
A.呼气酒精浓度K越大, 的阻值越小
B.当K=0时, 的阻值为100
C.当K=10时,该驾驶员为非酒驾状态
D.当 时,该驾驶员为醉驾状态
二、填空题
7.计划修建水渠1000米,则修建天数y和每日修建量x之间的函数关系式为 .
8.根据物理学知识,在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其函数图象如图所示,当时,该物体承受的压强p的值为 Pa.
三、解答题
9.已知 , 与x成反比例, 与 成正比例,并且当x=-1时,y=-15,当x=2时,y= ;求y与x之间的函数关系式.
四、作图题
10.如图,某物理实验装置由一个带刻度的无盖圆柱体玻璃筒和一个带托盘的活塞组成,该装置竖直放置时,活塞受到托盘中重物的压力向下压缩装置内的空气.某同学试着放上不同质量的物体,并根据筒侧的刻度记录活塞到筒底的距离,得到下面5组数据:
重物质量m/kg 2 3 4 6 8
活塞到桶底的距离h/cm 24 16 12 8 6
(1)以表中各组数据对应值为点的坐标,在如图直角坐标系中描出相应的点并用光滑的曲线连结.
(2)能否用学过的函数刻画变量h和m之间的关系?如果能,请求出h关于m的解析式;如果不能,请说明理由.
(3)要使活塞到筒底的距离大于5,请直接写出在托盘中放入重物的质量m的取值范围.
五、综合题
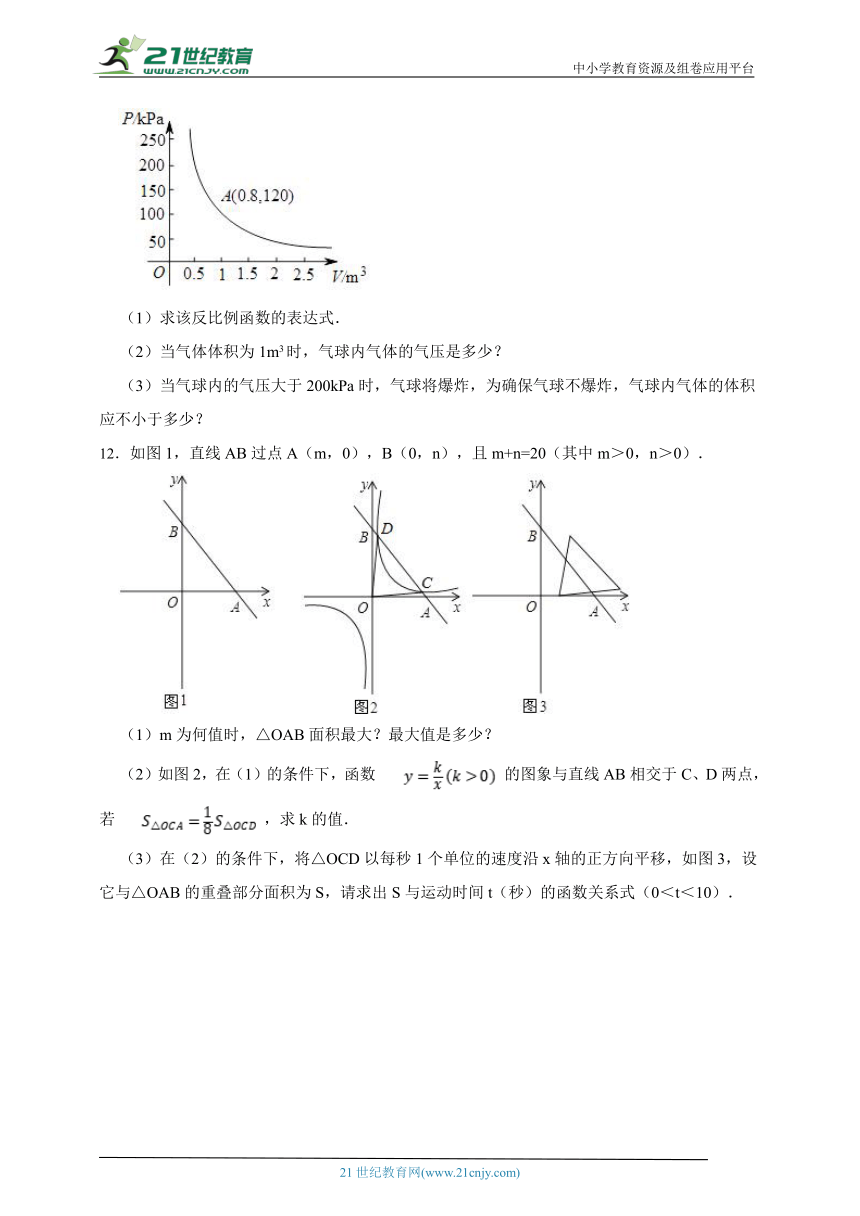
11.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求该反比例函数的表达式.
(2)当气体体积为1m3时,气球内气体的气压是多少?
(3)当气球内的气压大于200kPa时,气球将爆炸,为确保气球不爆炸,气球内气体的体积应不小于多少?
12.如图1,直线AB过点A(m,0),B(0,n),且m+n=20(其中m>0,n>0).
(1)m为何值时,△OAB面积最大?最大值是多少?
(2)如图2,在(1)的条件下,函数 的图象与直线AB相交于C、D两点,若 ,求k的值.
(3)在(2)的条件下,将△OCD以每秒1个单位的速度沿x轴的正方向平移,如图3,设它与△OAB的重叠部分面积为S,请求出S与运动时间t(秒)的函数关系式(0<t<10).
答案解析部分
1.【答案】B
【解析】【分析】根据题意,由等量关系“矩形的面积=底面周长×母线长”列出函数表达式再判断它们的关系则可。
【解答】由题意得2πrL=4,
则,
所以这个圆柱的母线长L和底面半径r之间的函数关系是反比例函数。
故选B.
【点评】熟记圆柱侧面积公式,列式整理出l、r的函数解析式是解题的关键。
2.【答案】D
【解析】【解答】观察图象可得,人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数关系是反比例函数,它的图象在第一象限,根据反比例函数的性质可知A,B错误,由图象可知当该村总人口为50人时,人均耕地面积为1公顷,选项D正确;该村人均耕地面积为2公顷,则总人口有25人,选项C错误,故答案为:D.
【分析】由图象可知当该村总人口为50人时,人均耕地面积为1公顷。
3.【答案】C
【解析】【解答】解:设近视镜的度数y(度)与镜片焦距x(米)的反比例函数解析式为 ,
∵小明佩戴的400度近视镜片的焦距为0.25米,
∴ ,
∴反比例函数解析式为 ,
∴当 时, ,
∴小明的近视镜度数可以调整为250度,
故答案为:C.
【分析】设近视镜的度数y(度)与镜片焦距x(米)的反比例函数解析式为 ,先求出函数解析式,再将代入计算即可。
4.【答案】C
【解析】【解答】解:设反比例函数关系式为:I= ,
把(2,3)代入得:k=2×3=6,
∴反比例函数关系式为:I= ,
当I≤3时,则 ≤3,
∴R≥2,
故答案为:C.
【分析】根据图像中的点的坐标,先求反比例函数关系式,再由电流不能超过三A列不等式,结合图像求出结论。
5.【答案】C
【解析】【解答】解:设 ,将 代入可得 ,故A错误;
∴蓄电池的电压是36V,故B错误;
当 时, ,该项正确;
当当 时, ,故D错误,
故答案为:C.
【分析】由已知条件:电流O(单位:A)与电阻R(单位:Ω)是反比例函数关系,由点(4,9),可求出此反比例函数解析式,可对A,B作出判断;再求出当I≤10A,可求出R的取值范围,可对C作出判断;然后将R=6Ω代入函数解析式,可求出I的值,可对D作出判断.
6.【答案】C
【解析】【解答】解:根据函数图象可得,
A、R随K 的增大而减小,则呼气酒精浓度K越大, R1的阻值越小,故正确,不符合题意;
B、 当K=0时, R1的阻值为100,故正确,不符合题意;
C、 当K=10时,则 ,该驾驶员为酒驾状态,故该选项不正确,符合题意;
D、当 R1=20 时, K=40 ,则 ,该驾驶员为醉驾状态,故该选项正确,不符合题意.
故答案为:C.
【分析】由图2直接判断A、B;由K=10时可算出M的值,从而判断C;观察图2可得R1=20时k值,从而算出M的值,即可判断D.
7.【答案】y=
【解析】【解答】根据工作总量=工作时间╳工作效率列关系式,1000=xy,
∴y= ;
故答案是:y= 。
【分析】本题主要考查反比例函数的应用,正确理解题意是解本题的关键.
8.【答案】400
【解析】【解答】解:设反比例函数的解析式为,
由图象得反比例函数经过点(0.1,1000),
∴,
∴反比例函数的解析式为,
当S=0.25时,.
故答案为:400
【分析】先求出反比例函数的解析式,再将S=0.25代入可得答案。
9.【答案】解:∵y1与x成反比例,y2与(x-2)成正比例,∴设y1= ,y2=k2(x-2),∴y= -k2(x-2),∵当x=-1时,y=-15,当x=2时,y= ;∴ ,解得 ,∴y与x之间的函数关系式为y= +4(x-2).
【解析】【分析】根据y1与x成反比例,y2与(x-2)成正比例,从而设出y1= ,y2=k2(x-2),又y = y 1 y 2,从而整体代入得y= -k2(x-2),再将x=-1,y=-15与x=2,y= 分别代入得出关于K1,K2的方程组,求解得出K1,K2的值,就可得出y与x之间的函数关系式。
10.【答案】(1)解:如图所示,平面直角坐标系中的曲线,就是所求的图象;
(2)解:猜想h和m符合反比例函数关系,
设,
将代入得:,∴
验证:当时,,符合题意,
∴h关于m的解析式为;
(3)
【解析】【解答】解:(3)当h>5时,即,
解得m<,
∴放入重物的质量m的取值范围为:.
【分析】(1)以表格中重物的质量作为点的横坐标,活塞到桶底的距离作为点的纵坐标,在 直角坐标系中描出相应的点并用光滑的曲线连结即可;
(2)观察发现:表格所给的重物的质量与活塞到桶底的距离的乘积等于一个定值“48”,故可得h和m符合反比例函数关系,进而利用待定系数法求出h关于m的函数解析式即可;
(3)令解析式中的h>5,可得关于字母m的不等式,求解即可.
11.【答案】(1)解:设ρ= ,
由题意知120= ,
所以k=96,
故ρ= (v>0)
(2)解:当v=1m3时,ρ=96,
∴气球内气体的气压是96kPa
(3)解:当p=200kPa时,v=
所以为了安全起见,气体的体积应不少于 m3
【解析】【分析】(1)设出反比例函数解析式,把A坐标代入可得函数解析式;(2)把v=1代入(1)得到的函数解析式,可得p;(3)把P=200代入得到V即可.
12.【答案】(1)解:∵A(m,0),B(0,n),
∴OA=m,OB=n.
∴S△AOB= .
∵m+n=20,
∴n=20﹣m,
∴S△AOB= =- m2+10m=﹣ (m﹣10)2+50
∵a=﹣ <0,
∴抛物线的开口向下,
∴m=10时,S最大=50
(2)解:∵m=10,m+n=20,
∴n=10,
∴A(10,0),B(0,10),
设AB的解析式为y=kx+b,由图象,得
,
解得: ,
y=﹣x+10.
∵ ,
∴设S△OCD=8a.则S△OAC=a,
∴S△OBD=S△OAC=a,
∴S△AOB=10a,
∴10a=50,
∴a=5,
∴S△OAC=5,
∴ OA y=5,
∴y=1.
1=﹣x+10,
x=9
∴C(9,1),
∴1= ,
∴k=9;
(3)解:移动后重合的部分的面积是△O′C′D′,t秒后点O的坐标为O′(t,0),
O′A=10﹣t,O′E=10.
∵C′D′∥CD,
∴△O′C′D′∽△O′CD,
∴ ,
∴
S=40 ,
∴ (0<t<10).
【解析】【分析】(1)由A(m,0),B(0,n),可以表示出OA=m,OB=n,由三角形的面积公式就可以求出结论;(2)由(1)的结论可以求出点A点B的坐标,就可以求出直线AB的解析式,根据双曲线的对称性就可以求出S△OBD=S△OAC的值,再由三角形的面积公式就可以求出其值;(3)根据平移的性质可以求得△O′C′D′∽△O′CD,再由相似三角形的性质就可以求出就可以求出S△O′C′D′和S△O′CD的面积关系,从而可以求出S与运动时间t之间的函数关系式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
26.2 实际问题与反比例函数一课一练
一、单选题
1.一个圆柱的侧面展开图是一个面积为4的矩形,这个圆柱的母线l与圆柱的底面半径r之间的函数关系是( )
A.正比例函数 B.反比例函数 C.一次函数 D.二次函数
2.某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为2公顷,则总人口有100人
D.当该村总人口为50人时,人均耕地面积为1公顷
3.研究发现,近视镜的度数y(度)与镜片焦距x(米)成反比例函数关系,小明佩戴的400度近视镜片的焦距为0.25米,经过一段时间的矫正治疗加之注意用眼健康,现在镜片焦距为0.4米,则小明的近视镜度数可以调整为( )
A.300度 B.500度 C.250度 D.200度
4.已知蓄电池的电压为定值.使用电池时,电流I(A)与电阻R(Ω)是反比例函数关系,图象如图所示.如果以此蓄电池为电源的电器的限制电流不能超过3A,那么电器的可变电阻R(Ω)应控制在( )
A.R≥1 B.0<R≤2 C.R≥2 D.0<R≤1
5.已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为I= B.蓄电池的电压是18V
C.当I≤10A时,R≥3.6Ω D.当R=6Ω时,I=4A
6.呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的 ), 的阻值随呼气酒精浓度K的变化而变化(如图2),血液酒精浓度M与呼气酒精浓度K的关系见图3.下列说法不正确的是( )
A.呼气酒精浓度K越大, 的阻值越小
B.当K=0时, 的阻值为100
C.当K=10时,该驾驶员为非酒驾状态
D.当 时,该驾驶员为醉驾状态
二、填空题
7.计划修建水渠1000米,则修建天数y和每日修建量x之间的函数关系式为 .
8.根据物理学知识,在压力不变的情况下,某物体承受的压强是它的受力面积的反比例函数,其函数图象如图所示,当时,该物体承受的压强p的值为 Pa.
三、解答题
9.已知 , 与x成反比例, 与 成正比例,并且当x=-1时,y=-15,当x=2时,y= ;求y与x之间的函数关系式.
四、作图题
10.如图,某物理实验装置由一个带刻度的无盖圆柱体玻璃筒和一个带托盘的活塞组成,该装置竖直放置时,活塞受到托盘中重物的压力向下压缩装置内的空气.某同学试着放上不同质量的物体,并根据筒侧的刻度记录活塞到筒底的距离,得到下面5组数据:
重物质量m/kg 2 3 4 6 8
活塞到桶底的距离h/cm 24 16 12 8 6
(1)以表中各组数据对应值为点的坐标,在如图直角坐标系中描出相应的点并用光滑的曲线连结.
(2)能否用学过的函数刻画变量h和m之间的关系?如果能,请求出h关于m的解析式;如果不能,请说明理由.
(3)要使活塞到筒底的距离大于5,请直接写出在托盘中放入重物的质量m的取值范围.
五、综合题
11.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求该反比例函数的表达式.
(2)当气体体积为1m3时,气球内气体的气压是多少?
(3)当气球内的气压大于200kPa时,气球将爆炸,为确保气球不爆炸,气球内气体的体积应不小于多少?
12.如图1,直线AB过点A(m,0),B(0,n),且m+n=20(其中m>0,n>0).
(1)m为何值时,△OAB面积最大?最大值是多少?
(2)如图2,在(1)的条件下,函数 的图象与直线AB相交于C、D两点,若 ,求k的值.
(3)在(2)的条件下,将△OCD以每秒1个单位的速度沿x轴的正方向平移,如图3,设它与△OAB的重叠部分面积为S,请求出S与运动时间t(秒)的函数关系式(0<t<10).
答案解析部分
1.【答案】B
【解析】【分析】根据题意,由等量关系“矩形的面积=底面周长×母线长”列出函数表达式再判断它们的关系则可。
【解答】由题意得2πrL=4,
则,
所以这个圆柱的母线长L和底面半径r之间的函数关系是反比例函数。
故选B.
【点评】熟记圆柱侧面积公式,列式整理出l、r的函数解析式是解题的关键。
2.【答案】D
【解析】【解答】观察图象可得,人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数关系是反比例函数,它的图象在第一象限,根据反比例函数的性质可知A,B错误,由图象可知当该村总人口为50人时,人均耕地面积为1公顷,选项D正确;该村人均耕地面积为2公顷,则总人口有25人,选项C错误,故答案为:D.
【分析】由图象可知当该村总人口为50人时,人均耕地面积为1公顷。
3.【答案】C
【解析】【解答】解:设近视镜的度数y(度)与镜片焦距x(米)的反比例函数解析式为 ,
∵小明佩戴的400度近视镜片的焦距为0.25米,
∴ ,
∴反比例函数解析式为 ,
∴当 时, ,
∴小明的近视镜度数可以调整为250度,
故答案为:C.
【分析】设近视镜的度数y(度)与镜片焦距x(米)的反比例函数解析式为 ,先求出函数解析式,再将代入计算即可。
4.【答案】C
【解析】【解答】解:设反比例函数关系式为:I= ,
把(2,3)代入得:k=2×3=6,
∴反比例函数关系式为:I= ,
当I≤3时,则 ≤3,
∴R≥2,
故答案为:C.
【分析】根据图像中的点的坐标,先求反比例函数关系式,再由电流不能超过三A列不等式,结合图像求出结论。
5.【答案】C
【解析】【解答】解:设 ,将 代入可得 ,故A错误;
∴蓄电池的电压是36V,故B错误;
当 时, ,该项正确;
当当 时, ,故D错误,
故答案为:C.
【分析】由已知条件:电流O(单位:A)与电阻R(单位:Ω)是反比例函数关系,由点(4,9),可求出此反比例函数解析式,可对A,B作出判断;再求出当I≤10A,可求出R的取值范围,可对C作出判断;然后将R=6Ω代入函数解析式,可求出I的值,可对D作出判断.
6.【答案】C
【解析】【解答】解:根据函数图象可得,
A、R随K 的增大而减小,则呼气酒精浓度K越大, R1的阻值越小,故正确,不符合题意;
B、 当K=0时, R1的阻值为100,故正确,不符合题意;
C、 当K=10时,则 ,该驾驶员为酒驾状态,故该选项不正确,符合题意;
D、当 R1=20 时, K=40 ,则 ,该驾驶员为醉驾状态,故该选项正确,不符合题意.
故答案为:C.
【分析】由图2直接判断A、B;由K=10时可算出M的值,从而判断C;观察图2可得R1=20时k值,从而算出M的值,即可判断D.
7.【答案】y=
【解析】【解答】根据工作总量=工作时间╳工作效率列关系式,1000=xy,
∴y= ;
故答案是:y= 。
【分析】本题主要考查反比例函数的应用,正确理解题意是解本题的关键.
8.【答案】400
【解析】【解答】解:设反比例函数的解析式为,
由图象得反比例函数经过点(0.1,1000),
∴,
∴反比例函数的解析式为,
当S=0.25时,.
故答案为:400
【分析】先求出反比例函数的解析式,再将S=0.25代入可得答案。
9.【答案】解:∵y1与x成反比例,y2与(x-2)成正比例,∴设y1= ,y2=k2(x-2),∴y= -k2(x-2),∵当x=-1时,y=-15,当x=2时,y= ;∴ ,解得 ,∴y与x之间的函数关系式为y= +4(x-2).
【解析】【分析】根据y1与x成反比例,y2与(x-2)成正比例,从而设出y1= ,y2=k2(x-2),又y = y 1 y 2,从而整体代入得y= -k2(x-2),再将x=-1,y=-15与x=2,y= 分别代入得出关于K1,K2的方程组,求解得出K1,K2的值,就可得出y与x之间的函数关系式。
10.【答案】(1)解:如图所示,平面直角坐标系中的曲线,就是所求的图象;
(2)解:猜想h和m符合反比例函数关系,
设,
将代入得:,∴
验证:当时,,符合题意,
∴h关于m的解析式为;
(3)
【解析】【解答】解:(3)当h>5时,即,
解得m<,
∴放入重物的质量m的取值范围为:.
【分析】(1)以表格中重物的质量作为点的横坐标,活塞到桶底的距离作为点的纵坐标,在 直角坐标系中描出相应的点并用光滑的曲线连结即可;
(2)观察发现:表格所给的重物的质量与活塞到桶底的距离的乘积等于一个定值“48”,故可得h和m符合反比例函数关系,进而利用待定系数法求出h关于m的函数解析式即可;
(3)令解析式中的h>5,可得关于字母m的不等式,求解即可.
11.【答案】(1)解:设ρ= ,
由题意知120= ,
所以k=96,
故ρ= (v>0)
(2)解:当v=1m3时,ρ=96,
∴气球内气体的气压是96kPa
(3)解:当p=200kPa时,v=
所以为了安全起见,气体的体积应不少于 m3
【解析】【分析】(1)设出反比例函数解析式,把A坐标代入可得函数解析式;(2)把v=1代入(1)得到的函数解析式,可得p;(3)把P=200代入得到V即可.
12.【答案】(1)解:∵A(m,0),B(0,n),
∴OA=m,OB=n.
∴S△AOB= .
∵m+n=20,
∴n=20﹣m,
∴S△AOB= =- m2+10m=﹣ (m﹣10)2+50
∵a=﹣ <0,
∴抛物线的开口向下,
∴m=10时,S最大=50
(2)解:∵m=10,m+n=20,
∴n=10,
∴A(10,0),B(0,10),
设AB的解析式为y=kx+b,由图象,得
,
解得: ,
y=﹣x+10.
∵ ,
∴设S△OCD=8a.则S△OAC=a,
∴S△OBD=S△OAC=a,
∴S△AOB=10a,
∴10a=50,
∴a=5,
∴S△OAC=5,
∴ OA y=5,
∴y=1.
1=﹣x+10,
x=9
∴C(9,1),
∴1= ,
∴k=9;
(3)解:移动后重合的部分的面积是△O′C′D′,t秒后点O的坐标为O′(t,0),
O′A=10﹣t,O′E=10.
∵C′D′∥CD,
∴△O′C′D′∽△O′CD,
∴ ,
∴
S=40 ,
∴ (0<t<10).
【解析】【分析】(1)由A(m,0),B(0,n),可以表示出OA=m,OB=n,由三角形的面积公式就可以求出结论;(2)由(1)的结论可以求出点A点B的坐标,就可以求出直线AB的解析式,根据双曲线的对称性就可以求出S△OBD=S△OAC的值,再由三角形的面积公式就可以求出其值;(3)根据平移的性质可以求得△O′C′D′∽△O′CD,再由相似三角形的性质就可以求出就可以求出S△O′C′D′和S△O′CD的面积关系,从而可以求出S与运动时间t之间的函数关系式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
