一元一次方程(行程问题)
图片预览






文档简介
课件19张PPT。一元一次方程的应用
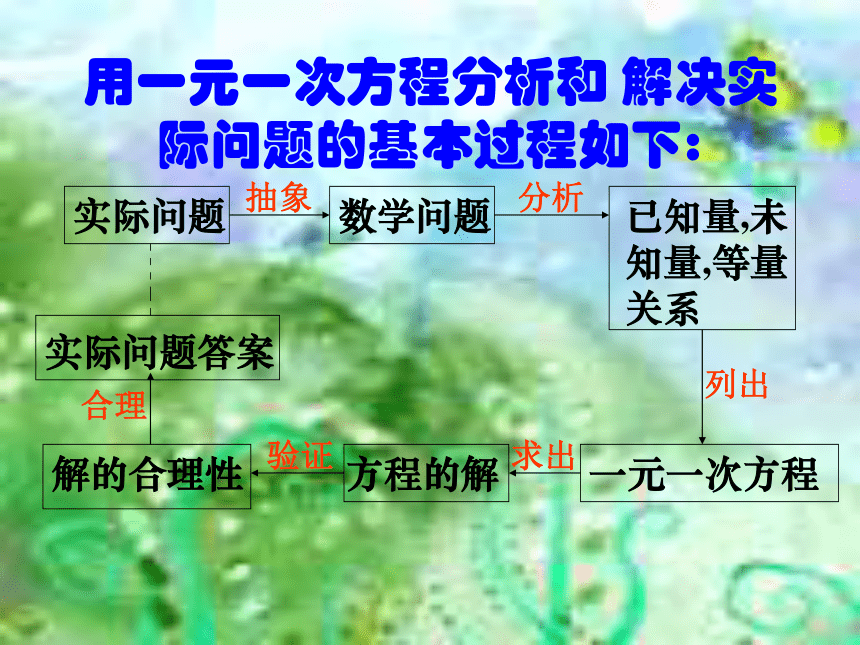
行程问题运用方程解决实际问题的一般过程是什么?1、审题:分析题意,找出题中的数量及其关系;2、设元:选择一个适当的未知数用字母表示(例如x);3、列方程:根据相等关系列出方程;4、解方程:求出未知数的值;5、检验:检查求得的值是否正确和符合实际情形,并写出答案。审设列解验6、答:把所求的答案答出来。答用一元一次方程分析和 解决实际问题的基本过程如下:实际问题数学问题已知量,未知量,等量关系一元一次方程方程的解解的合理性实际问题答案抽象分析列出求出验证合理一、明确行程问题中三个量的关系 引例:从甲地到乙地,水路比公路近40千米,上午十时,一艘轮船从甲地驶往乙地,下午1时一辆汽车从甲地驶往乙地,结果同时到达终点。已知轮船的速度是每小时24千米,汽车的速度是每小时40千米,求甲、乙两地水路、公路的长,以及汽车和轮船行驶的时间?三个基本量关系是:速度×时间=路程解:设水路长为x千米,则公路长为(x+40)千米等量关系:船行时间-车行时间=3小时答:水路长240千米,公路长为280千米,车行时间为
7小时,船行时间为10小时 依题意得:
x+40=280,x=240解2 设汽车行驶时间为x小时,则轮船行驶时间为
(x+3)小时。
等量关系:水路-公路=40依题意得:40x -24(x+3)= 40x=77+3=10 40×7=280 24 ×10=240
答:汽车行驶时间为7小时,船行时间为10小时,
公路长为280米,水路长240米。 引例:从甲地到乙地,水路比公路近40千米,上午十时,一艘轮船从甲地驶往乙地,下午1时一辆汽车从甲地驶往乙地,结果同时到达终点。已知轮船的速度是每小时24千米,汽车的速度是每小时40千米,求甲、乙两地水路、公路的长,以及汽车和轮船行驶的时间?一、相遇问题的基本题型1、同时出发(两段)二、相遇问题的等量关系2、不同时出发 (三段 )一、追及问题的基本题型1、不同地点同时出发二、追及问题的等量关系2、同地点不同时出发1、追及时快者行驶的路程-慢者行驶的路程=相距的 路程2、追及时快者行驶的路程=慢者行驶的路程或
慢者所用时间=快者所用时间+多用时间练习:1、两地相距28公里,小明以15公里/小时的速度。小亮以30公里/小时的速度,分别骑自行车和开汽车从同一地 前往另一地,小明先出发1小时,小亮几小时后才能
追上小明?解:设小亮开车x 小时后才能追上小明,则小亮所行路
程为30x公里,小明所行路程为15(x+1)
等量关系:小亮所走路程=小明所走路程
依题意得:30x=15(x+1)
x=1检验:两地相距28公里,在两地之间,小亮追不上小明则小明共走了2小时,共走了2×15=30公里答:在两地之间,小亮追不上小明2、甲、乙两人环绕周长是400米的跑道散步,如果两人从同一地点背道而行,那么经过2分钟他们两人就要相遇。
如果2人从同一地点同向而行,那么经过20分钟两人相 遇。如果甲的速度比乙的速度快,求两人散步的速度?
等量关系:甲行的路程-乙行的路程=环形周长答:甲速为每分钟110米,乙速为每分钟90米。注:同时同向出发:
快车走的路程-环行跑道周长=慢车走的路程(第一次相遇)
同时反向出发:
甲走的路程+乙走的路程=环行周长(第一次相遇)
解:设甲的速度为每分钟x 米,则乙的速度为每分钟
米。甲20分钟走了20x米,乙20分钟走了 米
依题意得:
x=110例 某连队从驻地出发前往某地执行任务,行军速度是
6千米/小时,18分钟后,驻地接到紧急命令,派遣
通讯员小王必须在一刻钟内把命令传达到该连队,
小王骑自行车以14千米/小时的速度沿同一路线追赶
连队,问是否能在规定时间内完成任务?
等量关系:小王所行路程=连队所行路程答:小王能在指定时间内完成任务。解:设小王追上连队需要x小时,则小王行驶的路程为
14x千米,连队所行路程是 千米依题意得:2.小明每天早上要在7:20之前赶到距家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上了他。
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远? 例 一列客车和一列货车在平行的轨道上同向行驶,
客车的长是200米,货车的长是280米,客车的
速度与货车的速度比是5 :3,客车赶上货车的
交叉时间是1分钟,求各车的速度;若两车相向
行驶,它们的交叉时间是多少分钟?
解:设客车的速度是5x米/分,
则货车的速度是3x米/分。
依题意得:5x – 3x = 280 + 200x=2405x = 1200,3x = 720设两车相向行驶的交叉时间为y分钟。依题意得:1200y+720y= 280 + 200y=0.25例题讲解:例 汽船从甲地顺水开往乙地,所用时间比从乙地逆水
开往甲地少1.5小时。已知船在静水的速度为18千米/小时,
水流速度为2千米/小时,求甲、乙两地之间的距离? 分析:本题是行程问题,但涉及水流速度,必须要
掌握:顺水速度=船速+水速
逆水速度=船速-水速
解:(直接设元)
设甲、乙两地的距离为x 千米
等量关系:逆水所用时间-顺水所用时间=1.5 依题意得: x=120
答:甲、乙两地的距离为120千米。
解2 (间接设元)
设汽船逆水航行从乙地到甲地需x 小时,
则汽船顺水航行的距离是(18+2)(x -1.5)千米,
逆水航行的距离是(18 -2)x千米。等量关系:汽船顺水航行的距离=汽船逆水航行的距离。 依题意得:(18+2)(x -1.5)= (18 -2)xx=7.5(18 -2) ×7.5=120
答:甲、乙两地距离为120千米。例1 汽船从甲地顺水开往乙地,所用时间比从乙地逆水
开往甲地少1.5小时。已知船在静水的速度为
18千米/小时,水流速度为2千米/小时,
求甲、乙两地之间的距离?例 一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时。已知水流的速度是3千米/时,求船在静水中的速度。分析:题中的等量关系为这艘船往返的路程相等,即:
顺流速度×顺流时间=逆流速度×逆流时间例 一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时。已知水流的速度是3千米/时,求船在静水中的速度。解:设船在静水中的平均速度为x千米/时,则顺流速度为(x+3)千米/时,逆流速度为(x-3)千米/时。根据往返路程相等,列得2(x+3)=2.5(x-3)去括号,得2x+6=2.5x-7.5移项及合并,得0.5x=13.5X=27答:船在静水中的平均速度为27千米/时。练习:
1、一架飞机飞行两城之间,顺风时需要5小时30分钟,
逆风时需要6小时,已知风速为每小时24公里,
求两城之间的距离?
等量关系:顺风时飞机本身速度=逆风时飞机本身速度。答:两城之间的距离为3168公里注:飞行问题也是行程问题。同水流问题一样,飞行问
题的等量关系有:顺风飞行速度=飞机本身速度+风速
逆风飞行速度=飞机本身速度-风速依题意得:
x=3168解:设两城之间距离为x 公里,则顺风速为 公
里/小时,逆风速为 公里/小时1、甲、乙两地相距162公里,一列慢车从甲站开出,每小时走48公里,一列快车从乙站开出,每小时走60公里试问: 1)两列火车同时相向而行,多少时间可以相遇?
2)两车同时反向而行,几小时后两车相距270公里?3)若两车相向而行,慢车先开出1小时,再用多少时间
两车才能相遇?4)若两车相向而行,快车先开25分钟,快车开了几小时
与慢车相遇?
5)两车同时同向而行(快车在后面),几小时后快车
可以追上慢车?6)两车同时同向而行(慢车在后面),几小时后两车相
距200公里?小结:
行程问题包括相遇、追击和飞行、航行的速度问题其基本关系是:路程=时间×速度相遇问题的等量关系:甲行距离+乙行距离=总路程 追击问题的等量关系:
1)同时不同地 :
慢者行的距离+两者之间的距离=快者行的距离
2)同地不同时:
甲行距离=乙行距离 或
慢者所用时间=快者所用时间+多用时间
顺水逆水的问题的等量关系:
1)顺水的路程 = 逆水的路程
2)顺速 – 逆速 = 2水速;顺速 + 逆速 = 2船速
行程问题运用方程解决实际问题的一般过程是什么?1、审题:分析题意,找出题中的数量及其关系;2、设元:选择一个适当的未知数用字母表示(例如x);3、列方程:根据相等关系列出方程;4、解方程:求出未知数的值;5、检验:检查求得的值是否正确和符合实际情形,并写出答案。审设列解验6、答:把所求的答案答出来。答用一元一次方程分析和 解决实际问题的基本过程如下:实际问题数学问题已知量,未知量,等量关系一元一次方程方程的解解的合理性实际问题答案抽象分析列出求出验证合理一、明确行程问题中三个量的关系 引例:从甲地到乙地,水路比公路近40千米,上午十时,一艘轮船从甲地驶往乙地,下午1时一辆汽车从甲地驶往乙地,结果同时到达终点。已知轮船的速度是每小时24千米,汽车的速度是每小时40千米,求甲、乙两地水路、公路的长,以及汽车和轮船行驶的时间?三个基本量关系是:速度×时间=路程解:设水路长为x千米,则公路长为(x+40)千米等量关系:船行时间-车行时间=3小时答:水路长240千米,公路长为280千米,车行时间为
7小时,船行时间为10小时 依题意得:
x+40=280,x=240解2 设汽车行驶时间为x小时,则轮船行驶时间为
(x+3)小时。
等量关系:水路-公路=40依题意得:40x -24(x+3)= 40x=77+3=10 40×7=280 24 ×10=240
答:汽车行驶时间为7小时,船行时间为10小时,
公路长为280米,水路长240米。 引例:从甲地到乙地,水路比公路近40千米,上午十时,一艘轮船从甲地驶往乙地,下午1时一辆汽车从甲地驶往乙地,结果同时到达终点。已知轮船的速度是每小时24千米,汽车的速度是每小时40千米,求甲、乙两地水路、公路的长,以及汽车和轮船行驶的时间?一、相遇问题的基本题型1、同时出发(两段)二、相遇问题的等量关系2、不同时出发 (三段 )一、追及问题的基本题型1、不同地点同时出发二、追及问题的等量关系2、同地点不同时出发1、追及时快者行驶的路程-慢者行驶的路程=相距的 路程2、追及时快者行驶的路程=慢者行驶的路程或
慢者所用时间=快者所用时间+多用时间练习:1、两地相距28公里,小明以15公里/小时的速度。小亮以30公里/小时的速度,分别骑自行车和开汽车从同一地 前往另一地,小明先出发1小时,小亮几小时后才能
追上小明?解:设小亮开车x 小时后才能追上小明,则小亮所行路
程为30x公里,小明所行路程为15(x+1)
等量关系:小亮所走路程=小明所走路程
依题意得:30x=15(x+1)
x=1检验:两地相距28公里,在两地之间,小亮追不上小明则小明共走了2小时,共走了2×15=30公里答:在两地之间,小亮追不上小明2、甲、乙两人环绕周长是400米的跑道散步,如果两人从同一地点背道而行,那么经过2分钟他们两人就要相遇。
如果2人从同一地点同向而行,那么经过20分钟两人相 遇。如果甲的速度比乙的速度快,求两人散步的速度?
等量关系:甲行的路程-乙行的路程=环形周长答:甲速为每分钟110米,乙速为每分钟90米。注:同时同向出发:
快车走的路程-环行跑道周长=慢车走的路程(第一次相遇)
同时反向出发:
甲走的路程+乙走的路程=环行周长(第一次相遇)
解:设甲的速度为每分钟x 米,则乙的速度为每分钟
米。甲20分钟走了20x米,乙20分钟走了 米
依题意得:
x=110例 某连队从驻地出发前往某地执行任务,行军速度是
6千米/小时,18分钟后,驻地接到紧急命令,派遣
通讯员小王必须在一刻钟内把命令传达到该连队,
小王骑自行车以14千米/小时的速度沿同一路线追赶
连队,问是否能在规定时间内完成任务?
等量关系:小王所行路程=连队所行路程答:小王能在指定时间内完成任务。解:设小王追上连队需要x小时,则小王行驶的路程为
14x千米,连队所行路程是 千米依题意得:2.小明每天早上要在7:20之前赶到距家1000米的学校上学,一天,小明以80米/分的速度出发,5分后,小明的爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度去追小明,并且在途中追上了他。
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远? 例 一列客车和一列货车在平行的轨道上同向行驶,
客车的长是200米,货车的长是280米,客车的
速度与货车的速度比是5 :3,客车赶上货车的
交叉时间是1分钟,求各车的速度;若两车相向
行驶,它们的交叉时间是多少分钟?
解:设客车的速度是5x米/分,
则货车的速度是3x米/分。
依题意得:5x – 3x = 280 + 200x=2405x = 1200,3x = 720设两车相向行驶的交叉时间为y分钟。依题意得:1200y+720y= 280 + 200y=0.25例题讲解:例 汽船从甲地顺水开往乙地,所用时间比从乙地逆水
开往甲地少1.5小时。已知船在静水的速度为18千米/小时,
水流速度为2千米/小时,求甲、乙两地之间的距离? 分析:本题是行程问题,但涉及水流速度,必须要
掌握:顺水速度=船速+水速
逆水速度=船速-水速
解:(直接设元)
设甲、乙两地的距离为x 千米
等量关系:逆水所用时间-顺水所用时间=1.5 依题意得: x=120
答:甲、乙两地的距离为120千米。
解2 (间接设元)
设汽船逆水航行从乙地到甲地需x 小时,
则汽船顺水航行的距离是(18+2)(x -1.5)千米,
逆水航行的距离是(18 -2)x千米。等量关系:汽船顺水航行的距离=汽船逆水航行的距离。 依题意得:(18+2)(x -1.5)= (18 -2)xx=7.5(18 -2) ×7.5=120
答:甲、乙两地距离为120千米。例1 汽船从甲地顺水开往乙地,所用时间比从乙地逆水
开往甲地少1.5小时。已知船在静水的速度为
18千米/小时,水流速度为2千米/小时,
求甲、乙两地之间的距离?例 一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时。已知水流的速度是3千米/时,求船在静水中的速度。分析:题中的等量关系为这艘船往返的路程相等,即:
顺流速度×顺流时间=逆流速度×逆流时间例 一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时。已知水流的速度是3千米/时,求船在静水中的速度。解:设船在静水中的平均速度为x千米/时,则顺流速度为(x+3)千米/时,逆流速度为(x-3)千米/时。根据往返路程相等,列得2(x+3)=2.5(x-3)去括号,得2x+6=2.5x-7.5移项及合并,得0.5x=13.5X=27答:船在静水中的平均速度为27千米/时。练习:
1、一架飞机飞行两城之间,顺风时需要5小时30分钟,
逆风时需要6小时,已知风速为每小时24公里,
求两城之间的距离?
等量关系:顺风时飞机本身速度=逆风时飞机本身速度。答:两城之间的距离为3168公里注:飞行问题也是行程问题。同水流问题一样,飞行问
题的等量关系有:顺风飞行速度=飞机本身速度+风速
逆风飞行速度=飞机本身速度-风速依题意得:
x=3168解:设两城之间距离为x 公里,则顺风速为 公
里/小时,逆风速为 公里/小时1、甲、乙两地相距162公里,一列慢车从甲站开出,每小时走48公里,一列快车从乙站开出,每小时走60公里试问: 1)两列火车同时相向而行,多少时间可以相遇?
2)两车同时反向而行,几小时后两车相距270公里?3)若两车相向而行,慢车先开出1小时,再用多少时间
两车才能相遇?4)若两车相向而行,快车先开25分钟,快车开了几小时
与慢车相遇?
5)两车同时同向而行(快车在后面),几小时后快车
可以追上慢车?6)两车同时同向而行(慢车在后面),几小时后两车相
距200公里?小结:
行程问题包括相遇、追击和飞行、航行的速度问题其基本关系是:路程=时间×速度相遇问题的等量关系:甲行距离+乙行距离=总路程 追击问题的等量关系:
1)同时不同地 :
慢者行的距离+两者之间的距离=快者行的距离
2)同地不同时:
甲行距离=乙行距离 或
慢者所用时间=快者所用时间+多用时间
顺水逆水的问题的等量关系:
1)顺水的路程 = 逆水的路程
2)顺速 – 逆速 = 2水速;顺速 + 逆速 = 2船速
