第二十二章 专题02二次函数的实际应用(30题) (含解析)2023-2024学年九年级数学上册人教版
文档属性
| 名称 | 第二十二章 专题02二次函数的实际应用(30题) (含解析)2023-2024学年九年级数学上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 23:08:48 | ||
图片预览




文档简介
专题第02讲 二次函数的实际应用(30题)
(2022秋 泰兴市期末)
1.一水果店售卖一种水果,以8元/千克的价格进货,经过往年销售经验可知:以12元/千克售卖,每天可卖60千克;若每千克涨价0.5元,每天要少卖2千克;若每千克降价0.5元,每天要多卖2千克,但不低于成本价.设该商品的价格为元/千克时,一天销售总质量为千克.
(1)求与的函数关系式.
(2)若水果店货源充足,每天以固定价格元/千克销售,试求出水果店每天利润与单价的函数关系式,并求出当为何值时,利润达到最大.
(2023 朝阳)
2.某超市以每件10元的价格购进一种文具,销售时该文具的销售单价不低于进价且不高于19元.经过市场调查发现,该文具的每天销售数量y(件)与销售单价x(元)之间满足一次函数关系,部分数据如下表所示:
销售单价x/元 … 12 13 14 …
每天销售数量y/元 … 36 34 32 …
(1)直接写出y与x之间的函数关系式;
(2)若该超市每天销售这种文具获利192元,则销售单价为多少元?
(3)设销售这种文具每天获利w(元),当销售单价为多少元时,每天获利最大?最大利润是多少元?
(2023 海淀区校级开学)
3.电缆在空中架设时,两端挂起的电缆下垂可以近似的看成抛物线的形状.如图,在一个斜坡上按水平距离间隔60米架设两个塔柱,每个塔柱固定电缆的位置离地面高度为27米(米),以过点A的水平线为x轴,水平线与电缆的另一个交点为原点O建立平面直角坐标系,如图所示.经测量,米,斜坡高度12米(即B、D两点的铅直高度差).
结合上面信息,回答问题:
(1)若以1米为一个单位长度,则D点坐标为_______,下垂电缆的抛物线表达式为_______.
(2)若电缆下垂的安全高度是13.5米,即电缆距离坡面铅直高度的最小值不小于13.5米时,符合安全要求,否则存在安全隐患.(说明:直线轴分别交直线和抛物线于点H、G.点G距离坡面的铅直高度为的长),请判断上述这种电缆的架设是否符合安全要求?请说明理由.
(2023春 江岸区校级月考)
4.如图,在斜坡底部点处安装一个的自动喷水装置,喷水头(视为点)的高度(喷水头距喷水装置底部的距离)是米,自动喷水装置喷射出的水流可以近似地看成抛物线.当喷射出的水流与喷水装置的水平距离为米时,达到最大高度米.以点为原点,自动喷水装置所在的直线为y轴,建立平面直角坐标系.
(1)求抛物线的解析式;
(2)斜坡上距离水平距离为米处有一棵高度为米的小树,垂直水平地面且点到水平地面的距离为米.
①记水流的高度为,斜坡的高度为,求的最大值(斜坡可视作直线OM);
②如果要使水流恰好喷射到小树顶端的点,直接写出自动喷水装置应向后平移(即抛物线向左)多少米?
(2023 武汉模拟)
5.如图,灌溉车为绿化带浇水,喷水口H离地竖直高度为1.2m.可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形,其水平宽度,竖直高度.下边缘抛物线是由上边缘抛物线向左平移得到,上边抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.4m,灌溉车到绿化带的距离为d(单位:m).
(1)求上边缘抛物线的函数解析式,并求喷出水的最大射程;
(2)求下边缘抛物线与x轴的正半轴交点B的坐标;
(3)要使灌溉车行驶时喷出的水能浇灌到整个绿化带,直接写出d的取值范围.
(2022秋 华容区期末)
6.农户销售某农产品,经市场调查发现:若售价为6元/千克,日销售量为40千克,若售价每提高1元/千克,日销售量就减少2千克.现设售价为元/千克(且为正整数).
(1)若某日销售量为24千克,求该日产品的单价;
(2)若政府将销售价格定为不超过18元/千克.设每日销售额为元,求关于的函数表达式,并求的最大值和最小值;
(3)市政府每日给农户补贴元后(为正整数),发现最大日收入(日收入=销售额+政府补贴)还是不超过450元,并且只有5种不同的单价使日收入不少于440元,请直接写出所有符合题意的的值.
(2023春 蔡甸区月考)
7.如图,抛物线,是某喷水器喷出的水抽象而成,抛物线由抛物线向左平移得到,把汽车横截面抽象为矩形,其中米,米,米,抛物线表达式为,,且点A,,,,均在坐标轴上.
(1)求抛物线表达式.
(2)求点的坐标.
(3)要使喷水器喷出的水能洒到整个汽车,记长为米,直接写出的取值范围.
(2022秋 华容区期末)
8.如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)运动员乙要抢到第二个落点D,他应再向前跑多少米 (取,)
(2023 淮安一模)
9.某网店销售一种文具袋,成本为30元/件,每天的销售量(件)与销售单价(元)之间满足一次函数关系,其图象如图所示.
(1)求与之间的函数关系式;
(2)如果规定每天的销量不低于240件,那么当销售单价为多少元时,每天获取的利润最大?最大利润是多少?
(2023 盘锦)
10.某工厂生产种产品,经市场调查发现,该产品每月的销售量y(件)与售价x(万元/件)之间满足一次函数关系.部分数据如下表:
每件售价x/万元 … 24 26 28 30 32 …
月销售量y/件 … 52 48 44 40 36 …
(1)求y与x的函数关系式(不写自变量的取值范围).
(2)该产品今年三月份的售价为35万元/件,利润为450万元.
①求:三月份每件产品的成本是多少万元?
②四月份工厂为了降低成本,提高产品质量,投资了450万元改进设备和革新技术,使每件产品的成本比三月份下降了14万元.若四月份每件产品的售价至少为25万元,且不高于30万元,求这个月获得的利润(万元)关于售价x(万元/件)的函数关系式,并求最少利润是多少万元?
(2023春 江都区月考)
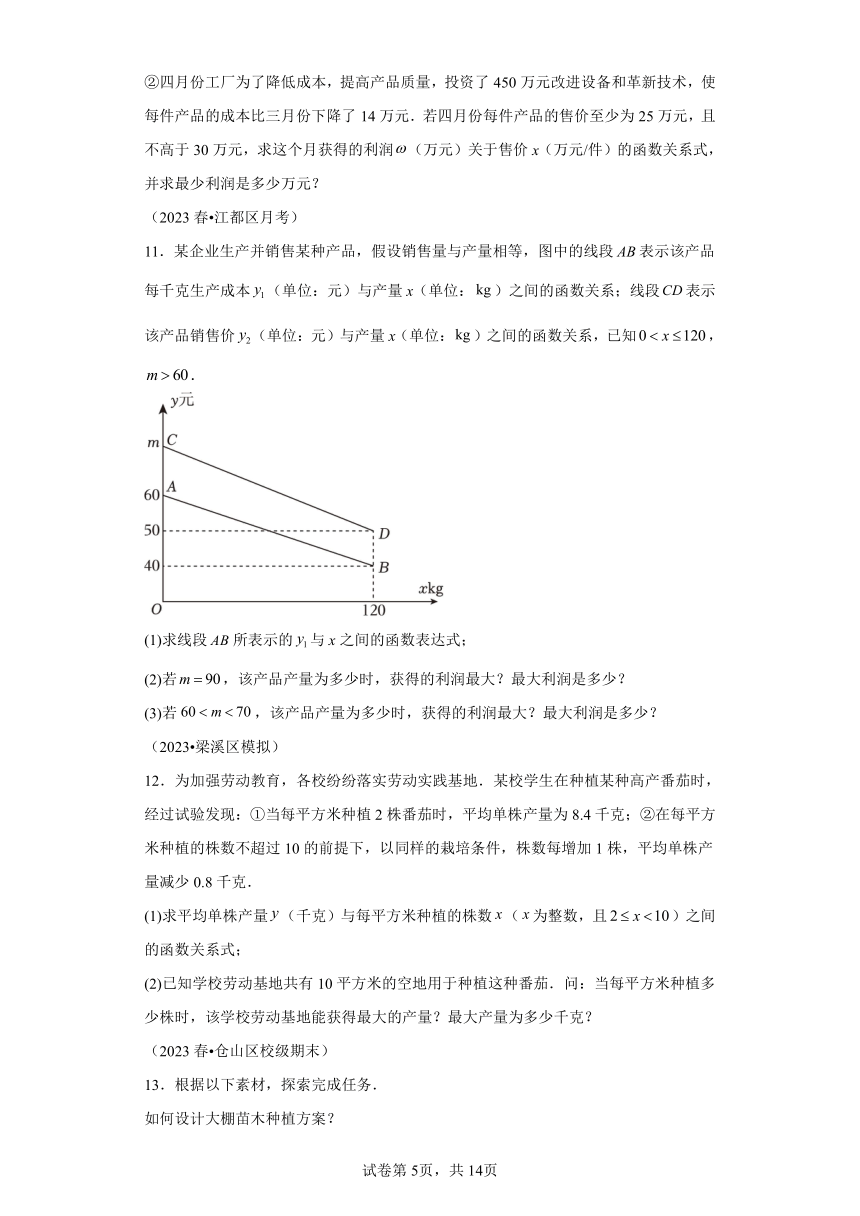
11.某企业生产并销售某种产品,假设销售量与产量相等,图中的线段表示该产品每千克生产成本(单位:元)与产量x(单位:)之间的函数关系;线段表示该产品销售价(单位:元)与产量x(单位:)之间的函数关系,已知,.
(1)求线段所表示的与x之间的函数表达式;
(2)若,该产品产量为多少时,获得的利润最大?最大利润是多少?
(3)若,该产品产量为多少时,获得的利润最大?最大利润是多少?
(2023 梁溪区模拟)
12.为加强劳动教育,各校纷纷落实劳动实践基地.某校学生在种植某种高产番茄时,经过试验发现:①当每平方米种植2株番茄时,平均单株产量为8.4千克;②在每平方米种植的株数不超过10的前提下,以同样的栽培条件,株数每增加1株,平均单株产量减少0.8千克.
(1)求平均单株产量(千克)与每平方米种植的株数(为整数,且)之间的函数关系式;
(2)已知学校劳动基地共有10平方米的空地用于种植这种番茄.问:当每平方米种植多少株时,该学校劳动基地能获得最大的产量?最大产量为多少千克?
(2023春 仓山区校级期末)
13.根据以下素材,探索完成任务.
如何设计大棚苗木种植方案?
素材1:图1中有一个大棚苗木种植基地及其截面图,其下半部分是一个长为,宽为的矩形,其上半部分是一条抛物线,现测得,大棚顶部的最高点距离地面.
素材:种植苗木时,每棵苗木高,为了保证生长空间,相邻两棵苗木种植点之间间隔,苗木顶部不触碰大棚,且种植后苗木成轴对称分布.
(1)任务1:确定大棚上半部分形状.根据图2建立的平面直角坐标系,通过素材1提供的信息确定点的坐标,求出抛物线的函数关系式;
(2)任务2:探究种植范围.在图2的坐标系中,在不影响苗木生长的情况下,确定种植点的横坐标的取值范围.
(2023 岳麓区校级二模)
14.从2020年开始,越来越多的商家向线上转型发展,“直播带货”已经成为商家的一种促销的重要手段.某商家在直播间销售一种进价为每件10元的日用商品,经调查发现,该商品每天的销售量y(件)与销售单价x(元)满足,设销售这种商品每天的利润为W(元).
(1)求W与x之间的函数关系式;
(2)该商家每天想获得1250元的利润,又要减少库存,应将销售单价定为多少元?
(3)若销售单价不低于28元,且每天至少销售50件时,求W的最大值.
(2022秋 蜀山区校级期末)
15.某超市经销甲、乙两种商品.商品甲每千克成本为20元,经试销发现,该种商品每天销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系,商品乙的成本为4元/千克,销售单价为10元/千克,但每天供货总量只有80千克,且能当天销售完.为了让利消费者,超市开展了“买一送一”活动,即买1千克的商品甲,免费送1千克的商品乙.
(1)直接写出销售量y与销售单价x之间的函数表达式______;
(2)设这两种商品的每天销售总额为S元,求出S(元)与x(元/千克)的函数关系式:(注:商品的销售额销售单价销售量)
(3)设这两种商品销售总利润为W,若商品甲的售价不低于成本,不超过成本的,当销售单价定为多少时,才能使当天的销售总利润最大?最大利润是多少?
(注:销售总利润两种商品的销售总额两种商品的总成本)
(2023春 莲池区校级期中)
16.为促进学生德智体美劳全面发展,推动文化学习与体育锻炼协调发展,某校举办了学生趣味运动会.该校计划用不超过元购买足球和篮球共个,分别作为运动会团体一、二等奖的奖品.已知足球单价元,篮球单价元.
(1)学校至多可购买多少个足球?
(2)受卡塔尔世界杯的影响,学校商议决定按(1)问的结果购买足球作为一等奖奖品,以鼓励更多学生热爱足球,同时商场也对足球和篮球的价格进行调整,足球单价下降了,篮球单价上涨了,最终学校购买奖品的经费比计划经费的最大值节省了元,求的值.
(2023春 宜都市期末)
17.某公司分别在A,B两城生产同种产品,共100件.A城生产产品的总成本(万元)与产品数量(件)之间具有一次函数关系:.当时,;当时,.B城生产产品的每件成本为7万元.
(1)求,的值;
(2)当A,B两城生产这批产品的总成本之和为660万元时,求A,B两城各生产产品多少件?
(3)从A城把该产品运往C,D两地的费用分别为万元/件和3万元/件;从B城把该产品运往C,D两地的费用分别为1万元/件和2万元/件.C地需要90件,D地需要10件,在(2)的条件下,若A,B两城总运费之和的最小值为150万元,求的值.
(2023 海淀区校级四模)
18.某公园修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安装一个可调节角度的喷水头,从喷水头喷出的水柱形状是一条抛物线.建立如图所示的平面直角坐标系,抛物线形水柱的竖直高度(单位:m)与到池中心的水平距离(单位:m)满足的关系式近似为().
(1)在某次安装调试过程中,测得与的部分对应值如下表:
水平距离 0 0.5 1 1.5 2 2.5 3
竖直高度 2.25 2.8125 3 2.8125 2.25 1.3125 0
根据表格中的数据,解答下列问题:
①水管的长度是______m;
②求出与满足的函数解析式();
(2)安装工人在上述基础上进行了下面两种调试:
①不改变喷水头的角度,将水管长度增加1m,水柱落地时与池中心的距离为;
②不改变水管的长度,调节喷水头的角度,使得水柱满足,水柱落地时与池中心的距离为.则比较与的大小关系是:______(填“”或“”或“”)
(2023 罗山县三模)
19.实心球是中考体育项目之一.在掷实心球时,实心球被掷出后的运动路线可以看作是抛物线的一部分,已知小军在一次掷实心球训练中,第一次投掷时出手点距地面1.8m,实心球运动至最高点时距地面3.4m,距出手点的水平距离为4m.设实心球掷出后距地面的竖直高度为y(m),实心球距出手点的水平距离为x(m).如图,以水平方向为x轴,出手点所在竖直方向为y轴建立平面直角坐标系.
(1)求第一次掷实心球时运动路线所在抛物线的表达式.
(2)若实心球投掷成绩(即出手点与着陆点的水平距离)达到12.4m为满分,请判断小军第一次投掷实心球能否得满分.
(3)第二次投掷时,实心球运动的竖直高度y与水平距离x近似满足函数关系.记小军第一次投掷时出手点与着陆点的水平距离为,第二次投掷时出手点与着陆点的水平距离为,则______(填“>”“<”“=”).
(2023 花溪区校级一模)
20.过山车是一项富有刺激性的娱乐工具,在乘坐过山车的过程能够亲身体验由能量守恒、加速度和力交织在一起产生的效果,那感觉真是妙不可言.如图是合肥某乐园中部分过山车滑道所抽象出来的函数图象,线段是一段直线滑道,且长为米,点到地面距离米,点到地面距离米,滑道可以看作一段抛物线,最高点为.
(1)求滑道部分抛物线的函数表达式;
(2)当小车(看成点)沿滑道从运动到的过程中,小车距离轴的垂直距离为2.5米时,它到出发点的水平距离是多少?
(3)现在需要对滑道部分进行加固,建造某种材料的水平和竖直支架,,.已知这种材料的价格是75000元/米,为了预算充足,至少需要申请多少元的资金.
(2022秋 丰都县期末)
21.掷实心球是丰都中考体育考试项目之一,如图1是一名男生投实心球情境,实心球行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示、掷出时,起点处高度为1.9m,当水平距离为4m时,实心球行进至最高点3. 5m处.
(1)求y关于x的函数表达式:
(2)根据中考体育考试评分标准(男生版),投掷过程中,实心球从起点到落地点的水平距离大于等于9.7m时,即可得满分10分,该男生在此项考试中能否得满分,请说明理由.
(2022秋 建昌县期末)
22.2022年11月,“中国传统制茶技艺及其相关习俗”申遗成功,弘扬茶文化,倡导“和美雅静”的生活方式已成时尚.某茶商经销某品牌茶,成本为50元/千克,经市场调查发现,每周的销量(千克)与销售单价(元/千克)满足一次函数关系,部分数据列表如下:
销售单价(元/千克) 56 65 75 …
销量(千克) 128 110 90 …
(1)求与的一次函数关系式;
(2)求该茶商这一周销售该品牌茶叶所获利润(元)的最大值.
(2023 锦州二模)
23.近年来国家出台政策要求电动车上牌照,“保安全、戴头盔”出行.某头盔专卖店购进一批单价为36元的头盔,在销售中,通过分析销售情况发现这种头盔的月销售量(个)与售价(元/个)满足一次函数关系,表格是其中的两组对应值.
售价(元/个) … 50 55 …
月销售量(个) … 100 90 …
(1)求与之间的函数关系式;
(2)专卖店的优惠活动:若购买一个这种头盔,就赠送一个成本为6元的头盔面罩.请问这种头盔的售价定为多少元时,月销售利润最大,最大月销售利润是多少元?
(2023 金湖县三模)
24.某超市购进甲、乙两种商品,已知购进5件甲商品和2件乙商品,需80元;购进3件甲商品和4件乙商品,需90元.
销售单价x(元/件) 12 18
日销售量y(件) 16 4
(1)甲、乙两种商品的进货单价分别是多少?
(2)设甲商品的销售单价为x(单位:元/件),在销售过程中发现:当时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:
请写出当时,y与x之间的函数关系式.
(3)在(2)的条件下,设甲商品的日销售利润为w元,当甲商品的销售单价x(元件)定为多少时,日销售利润最大?最大利润是多少?
(2022秋 新抚区期末)
25.疫情防控常态化,全国人民同心抗疫.某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售,市场调查发现,线下的月销量y(件)与线下售价x(元/件,且)之间满足一次函数关系,部分数据如下表:
x(元/件) 12 13 14 15
y(件) 1000 900 800 700
(1)求y与x之间的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为600件.当x为何值时,线上和线下销售月利润总和W达到最大?最大利润是多少?
(3)要使(2)中月利润总和W不低于4400元,请直接写出x的取值范围.
(2023 嘉鱼县模拟)
26.为巩固扶贫攻坚成果,我县政府督查各部门和单位对口扶贫情况.某单位的帮扶对象种植的农产品在某月(按30天计)的第x天(x为正整数)的销售价格p(元/千克)关于x的函数关系为,销售量y(千克)与x之间的关系如图所示.
(1)直接写出y与x之间的函数关系式和x的取值范围;
(2)求该农产品的销售量有几天不超过60千克?
(3)当月第几天,该农产品的销售额最大,最大销售额是多少?(销售额=销售量×销售价格)
(2023 云梦县校级三模)
27.李丽大学毕业后回家乡创业,开了一家服装专卖店代理品牌服装的销售.已知该品牌服装进价每件40元,日销售(件)与销售价(元/件)之间的关系如图所示(实线),每天付员工的工资每人82元,每天应支付其他费用106元.
(1)直接写出日销售(件)与销售价(元/件)之间的函数关系式;
(2)当某天的销售价为48元/件时,收支恰好平衡(收入=支出),求该店员工人数;
(3)若该店只有2名员工,则每天能获得的最大利润是多少元 此时,每件服装的价格应定为多少元
(2023 卧龙区二模)
28.如图,在斜坡底部点O处安装一个自动喷水装置,喷水头(视为点A)的高度(喷水头距喷水装置底部的距离)是米,自动喷水装置喷射出的水流可以近似地看成抛物线.当喷射出的水流与喷水装置的水平距离为米时,达到最大高度米.以点O为原点,自动喷水装置所在的直线为y轴,建立平面直角坐标系.
(1)求抛物线的函数关系式;
(2)斜坡上距离O水平距离为米处有一棵高度为米的小树,垂直水平地面,且M点到水平地面的距离为2米,绿化工人向左水平移动喷水装置后,水流恰好喷射到小树顶端的点N,求自动喷水装置向左水平平移(即抛物线向左)了多少米?
(2023 竞秀区二模)
29.过山车是一项富有刺激性的娱乐工具,深受年轻游客的喜爱.某游乐场修建了一款大型过山车.如图所示,为这款过山车的一部分轨道(B为轨道最低点),它可以看成一段抛物线,其中米,米(轨道厚度忽略不计).
(1)求抛物线的函数表达式;
(2)在轨道上有两个位置P和C到地面的距离均为n米,当过山车运动到C处时,又进入下坡段(接口处轨道忽略不计,E为轨道最低点),已知轨道抛物线的形状与抛物线完全相同,E点坐标为,求n的值;
(3)现需要对轨道下坡段进行安全加固,建造某种材料的水平和竖直支架,且要求,已知这种材料的价格是100000元/米,请计算多长时,造价最低?最低造价为多少元?
(2023 利辛县模拟)
30.如图,某小区的景观池中安装一雕塑,米,喷出两股水流,两股水流可以抽象为平面直角坐标系中的两条抛物线(图中的,)的部分图象,两条抛物线的形状相同且顶点的纵坐标相同,且经测算发现抛物线的最高点(顶点)C距离水池面米,且与的水平距离为2米.
(1)求抛物线的解析式;
(2)求抛物线与x轴的交点B的坐标;
(3)小明同学打算操控微型无人机在,之间飞行,为了无人机的安全,要求无人机在竖直方向上的活动范围不小于米,设无人机与的水平距离为m,求m的取值范围.
试卷第2页,共14页
试卷第1页,共14页
参考答案:
1.(1)
(2),
【分析】(1)设该商品的价格为元/千克,根据“以12元/千克售卖,每天可卖60千克;若每千克涨价0.5元,每天要少卖2千克;若每千克降价0.5元,每天要多卖2千克,但不低于成本价”,得到销售总质量与的函数关系式.
(2)根据利润=每千克利润×销售总质量,得到有关利润的二次函数求最值即可;
【详解】(1)由题意可得,
(2)由题意可得,
当时,利润达到最大
答:当为时,利润达到最大
【点睛】本题主要考查了二次函数的应用,解题的关键是了解利润和售价,销售量之间的关系.
2.(1)
(2)18元
(3)19元,198元
【分析】(1)利用待定系数法求解即可;
(2)根据题意可列出关于x的一元二次方程,解出x的值,结合x的取值范围求解即可;
(3)根据题意可列出w与x的函数关系式,再根据二次函数的性质求解即可.
【详解】(1)解:设y与x之间的函数关系式为,由所给表格可知:
,解得:,
故y与x的函数关系式为;
(2)解:根据题意得:,
解得:.
又∵,
∴,
答:销售单价应为18元.
(3)解:,
∵,
∴抛物线开口向下.
∵对称轴为直线,
∴当时,w随x的增大而增大,
∴当时,w有最大值,.
答:当销售单价为19元时,每天获利最大,最大利润是198元.
【点睛】本题考查一次函数、二次函数的实际应用,一元二次方程的实际应用.理解题意,找出等量关系,列出等式是解题关键.
3.(1),
(2)这种电缆的架设符合安全要求,理由见解析
【分析】(1)由题意可求出米,米,即得出.又可求出米,即得出.结合,利用待定系数法求解即可;
(2)利用待定系数法可求出斜坡解析式为,即可求出电缆与坡面的铅直高度.再根据二次函数的性质求解即可.
【详解】(1)由题意得:米,米,米,米,轴,轴,
∴米,米,
∴.
∵米,
∴.
∵,
∴设下垂电缆的抛物线表达式为:,
∴,
解得:,
∴下垂电缆的抛物线表达式为:.
故答案为:,;
(2)这种电缆的架设符合安全要求,理由如下:
由(1)可知:,,,
设斜坡解析式为,
∴,解得:
∴斜坡解析式为,
则电缆与坡面的铅直高度.
∵,
∴当时,有最小值为18,即,
∴这种电缆的架设符合安全要求.
【点睛】本题考查二次函数的实际应用,一次函数的实际应用.理解题意,正确求出二次函数和一次函数解析式是解题关键.
4.(1)
(2)①最大值为;②喷射架应向后移动米
【分析】(1)根据当喷射出的水流距离喷水头米时,达到最大高度米,设设水流形成的抛物线为,代入点求出二次函数的解析式,即可求解;
(2)①先求出斜坡的高度的解析式,列出,把函数解析式化为顶点式,即可求解;
②设喷射架向后平移了米,设出平移后的函数解析式,代入点的坐标即可求解.
【详解】(1)解:由题可知:当喷射出的水流距离喷水头米时,达到最大高度米,
则可设水流形成的抛物线为 ,
将点代入可得,
∴抛物线为
(2)①解:由题可知点坐标为,
设直线的解析式为,
把点的坐标代入得
,
解得
则直线为
的最大值为.
②解:设喷射架向后平移了米,则平移后的抛物线可表示为
将点代入得:
解得或 舍去
喷射架应向后移动米.
【点睛】此题考查了二次函数在实际问题中的应用,根据题意求出函数的解析式是解决此题的关键.
5.(1);6m
(2)
(3)
【分析】(1)由顶点得,设,再根据抛物线过点,可得a的值,从而解决问题;
(2)由对称轴知点的对称点为,则下边缘抛物线是由上边缘抛物线向左平移4m得到的,可得点B的坐标;
(3)根据EF=0.5,求出点F的坐标,利用增减性可得d的最大值为最小值,从而得出答案.
【详解】(1)解:如图,由题意得是上边缘抛物线的顶点,
设,
又∵抛物线过点,∴,
∴,
∴上边缘抛物线的函数解析式为,当时,,
解得,(舍去),
∴喷出水的最大射程为6m;
(2)解:∵对称轴为直线,
∴点的对称点为,
∴下边缘抛物线是由上边缘抛物线向左平移4m得到的,
∴点B的坐标为;
(3)解:∵,
∴点F的纵坐标为0.5,
∴,解得,
∵,
∴,
当时,y随x的增大而减小,
∴当时,要使,
则 ,
∵当时,y随x的增大而增大,且时,,
∴当时,要使,则,
∵,灌溉车行驶时喷出的水能浇灌到整个绿化带,
∴d的最大值为,
再看下边缘抛物线,喷出的水能浇灌到绿化带底部的条件是,
∴d的最小值为2,
综上所述,d的取值范围是.
【点睛】本题是二次函数的实际应用,主要考查了待定系数法求二次函数解析式,二次函数的性质,二次函数与方程的关系等知识,读懂题意,建立二次函数模型是解题的关键.
6.(1)14
(2),最大338元,最小240元
(3)
【分析】(1) 售价为元/千克(且为正整数),则提价元,故销售量为千克,根据题意,列方程计算即可.
(2) 根据日销售额=日售价×日销售量,计算即可.
(3)由题意得:,由二次函数的对称性可知x的取值为11,12,13,14,15,从而计算可得a值.
【详解】(1)解:设产品售价为元/千克(且为正整数),则提价元,
故销售量为千克,
根据题意,得,
解得,
故该日产品的单价为14元/千克.
(2)解:设售价为元/千克(且为正整数),销售额为元,则提价元,
故销售量为千克,
∴,
∴,
∵,且对称轴右侧,y随x的增大而减小,到对称轴距离越大,函数值越小,且,
∴时,w取得最大值,且最大值为338元,
∴时,w取得最小值,且最小值为240元,
故,w的最大338元,w的最小240元.
(3)解:由题意得:,由二次函数的对称性可知x的取值为11,12,13,14,15,
∴时,元
∴时,元,
∴时,元,
且,
∴,
∵a是正整数,
∴a的值为.
【点睛】本题主要考查二次函数的应用.得到每天可售出的千克数是解决本题的突破点;本题需注意x的取值应为整数.解题的关键是熟练掌握待定系数法求函数解析式、根据销售额的相等关系列出函数解析式及二次函数的性质.
7.(1)
(2)
(3)
【分析】(1)分别把、点坐标代入解析式即可解答;
(2)由题意易得抛物线是由抛物线向左平移4米得到的,则有抛物线表达式为:,然后把代入求解即可;
(3)由(2)可得,又因为,即可解答
【详解】(1)解:把代入,得:
,
∵,
∴把代入,
解得,
抛物线表达式:,
当时,即,
解得:,
,,
抛物线表达式:;
(2)解:,
、的纵坐标为,
,
解得:,,
点的纵坐标是,
抛物线是由抛物线向左平移4米得到的,
抛物线表达式为:,
把代入,得:
,
解得,(舍去),
,
(3)解:由(2)可得点坐标为,,
,
由(1)得把代入,得,(舍去),
,,
,
【点睛】本题是二次函数的实际应用,主要考查了待定系数法求二次函数解析式,二次函数的性质,二次函数与方程的关系等知识,读懂题意,建立二次函数模型是解题的关键.
8.(1); (2)17米.
【分析】(1)易得第一次落地时抛物线的顶点,可设所求的函数解析式为顶点式,把(0,1)代入即可求得所求的函数解析式;
(2)易得第二次落地时的抛物线的二次项的系数与第一次落地时抛物线的二次项系数相同,顶点的纵坐标为第一个函数顶点纵坐标的一半,用顶点式设出所求的函数解析式,把C坐标代入后求得第二次落地时的抛物线解析式,让函数值等于0可得D的横坐标,减去OB的距离即为跑的距离.
【详解】(1)如图,设第一次落地时,抛物线的表达式为y=a(x-6)2+4.
由已知:当x=0时y=1.即1=36a+4,
∴a=-.
∴表达式为y=-(x-6)2+4=;
(2)由题意得:0=-(x-6)2+4
解得:x1=4+6≈13,x2=-4+6<0(舍去),
∴点C坐标为(13,0).
设第二次落地的抛物线为y=-(x-k)2+2.
将C点坐标代入得:0=-(13-k)2+2.
解得:k1=13-2<13(舍去),k2=13+2≈18.
∴y=-(x-18)2+2.
0=-(x-18)2+2.
x1=18-2(舍去),x2=18+2≈23,
∴BD=23-6=17(米).
答:运动员乙要抢到第二个落点D,他应再向前跑17米.
【点睛】本题考查了二次函数的应用;判断出两个二次函数的顶点坐标是解题的关键;用到的知识点为:若二次函数的形状相同,则两个二次函数的二次项系数相同.
9.(1)y=-10x+700; (2)当销售单价为46元时,每天利润最大,为3840元.
【分析】(1)利用待定系数法求解可得;
(2)根据“总利润每件利润销售量”列出函数解析式,并配方成顶点式,再结合的取值范围,利用二次函数的性质求解可得.
【详解】解:(1)设,
将、代入,得:,
解得:,
则;
(2)设每天获取的利润为,
则
,
又,
,
时,随的增大而增大,
当时,取得最大值,最大值为,
答:当销售单价为46元时,每天获取的利润最大,最大利润是3840元.
【点睛】本题主要考查了待定系数法求函数解析式及二次函数的应用,解题的关键是理解题意,找到题目蕴含的相等关系,并熟练掌握二次函数的性质求最大值.
10.(1)
(2)①20万元;②,950万元
【分析】(1)从表格中任选两组数据,利用待定系数法求解;
(2)利用(1)中结论求出3月份销量,根据利润、销量、成本、售价之间的关系列方程即可;②列关于x的二次函数关系式,结合自变量的取值范围求出函数的最值即可.
【详解】(1)解:设y与x的函数关系式为,将,代入,得:
,
解得,
y与x的函数关系式为;
(2)解:①将代入,得(件),
设三月份每件产品的成本是a万元,
由题意得,
解得,
即三月份每件产品的成本是20万元;
②四月份每件产品的成本比三月份下降了14万元,
四月份每件产品的成本为万元,
由题意得:,
,
抛物线的图象开口向下,
抛物线的对称轴为,,
时,取最小值,此时,
综上可知,关于售价x的函数关系式是,最少利润是950万元.
【点睛】本题考查一次函数、二次函数的实际应用,解题的关键是根据利润、销量、成本、售价之间的关系正确列出函数关系式.
11.(1)
(2),最大利润是1350元
(3),最大利润为1200元
【分析】(1)利用待定系数法直接求解即可;
(2)根据题意利用待定系数法可求出与x之间的函数表达式为.设获得的利润为w元,再根据利润=(销售价-成本)×产量可求出w与x的函数关系式,最后根据二次函数的性质求解即可;
(3)利用待定系数法可求出与x之间的函数表达式为,设获得的利润为元,则.又可求出,,即得出,即抛物线对称轴在y轴左侧,从而得出当时,随x的增大而增大,再根据二次函数的性质求解即可.
【详解】(1)设线段所表示的与x之间的函数表达式为,
将代入得:,
解得:,
∴线段所表示的与x之间的函数表达式为;
(2)若,设与x之间的函数表达式为,
根据题意得:,
解得:,
∴.
设获得的利润为w元,
根据题意得:,
∵,,
∴当时,w有最大值,最大值为1350元.
∴若,该产品产量为时,获得的利润最大,最大利润是1350元;
(3)设,由题意得:
,
解得:,
∴,
设获得的利润为元,
∴.
∵,
∴,,
∴,即抛物线对称轴在y轴左侧,
∴当时,随x的增大而增大,
∴当时,的值最大,元,
∴时,该产品产量为时,获得的利润最大,最大利润为1200元.
【点睛】本题主要考查待定系数求一次函数解析式及二次函数的实际应用能力,根据相等关系列出函数关系式,熟练根据二次函数的性质判断函数的最值情况是解题的关键.
12.(1)(,且为整数)
(2)6株,312千克
【分析】(1)根据题意,找出数量关系式,即可求出平均单株产量(千克)与每平方米种植的株数之间的函数关系式;
(2)利用总产量平均的产量种植的株数,列关于的一元二次方程,将其转化为顶点式,根据为整数,即可求出种多少株最大产量,以及最大产量多少.
【详解】(1)解:每平方米种植的株数每增加1株,单株产量减少0.8千克,
,
关于的函数表达式为(,且为整数);
故答案为:(,且为整数).
(2)解:设每平方米番茄产量为千克,
根据题意得:
,为整数,
当时,取最大值,最大值为,
(千克),
答:每平方米种植6株时,该学校劳动基地能获得最大的产量,最大产量为312千克.
【点睛】本题考查了一次函数和二次函数的综合运用,解题的关键需要找出和存在的关系,以及熟练掌握顶点式二次函数表达式.
13.(1)
(2)确定种植点的横坐标的取值范围为
【分析】(1)根据题意建立直角坐标系,分别得到,,,再根据待定系数法即可求出二次函数的解析式;
(2)根据每棵苗木高,且苗木顶部不触碰大棚得到,即可求出种植点的横坐标的取值范围;
【详解】(1)解:如下图所示,
根据题意得,,,,
设二次函数的解析式为,
得,
解方程组得,,
∴;
(2)当时,
得,
∴,
∴;
【点睛】本题考查二次函数的应用,解题的关键是根据题意求出抛物线的解析式.
14.(1),
(2)15元
(3)2160元
【分析】(1)利用利润等于单价利润乘以销售数量列出函数关系式即可;
(2)令,解一元二次方程即可;
(3)根据二次函数的性质,求最值即可.
【详解】(1)解:根据题意,有:,
化简,得:,
由题意:,解得:,
即函数关系为:,;
(2)令,可得:,
解得:,或者,
当时,销量:(件);
当时,销量:(件);
销量越高,越有利于减少库存,
即为了减少库存,将销售单价应定为15元;
(3)根据题意有:,解得:,
∵,,
∴当时,函数值随着x的增大而减小,
∵,
∴当时,函数值最大,最大为:.
答:此时W的最大值为2160元.
【点睛】本题考查二次函数的实际应用.读懂题意,正确的列出函数解析式,利用二次函数的性质进行求解,是解题的关键.
15.(1)
(2)
(3)当销售单价定为30元时,才能使当天的销售总利润最大,最大利润是240元
【分析】(1)利用待定系数法可求出一次函数的解析式;
(2)利用商品的销售额销售单价销售量,即可求出(元)与的函数关系式;
(3)利用销售总利润两种商品的销售总额两种商品的总成本求出两种商品销售总利润为W与销售单价之间的关系式,根据已知求出的取值范围,再将关系式化为配方式,然后根据二次函数的性质来进行计算即可.
【详解】(1)解:设与之间的函数表达式为,
将图象中、代入得:,解得:,
∴销售量y与销售单价x之间的函数表达式为:,
故答案为:;
(2)∵超市开展了“买一送一”活动,即买1千克的商品甲,免费送1千克的商品乙,且商品乙每天供货总量只有80千克,
∴商品甲的销量:,即,
∴,
则两种商品的每天销售总额:;
(3)两件商品的成本为:元,
∵商品甲的售价不低于成本,不超过成本的,,
∴,
,
即,
∵,
∴时,随的增大而增大,
∴时,的最大值,
答:当销售单价定为30元时,才能使当天的销售总利润最大,最大利润是240元.
【点睛】本题考查了待定系数法求一次函数的解析式和二次函数在实际问题中的应用,理清题中的数量关系是解题的关键.
16.(1)学校至多可购买个足球
(2)的值为
【分析】(1)设学校购买个足球,则购买个篮球,根据总价单价数量结合总费用不超过元,即可得出关于的一元一次不等式,解不等式即可得出结论;
(2)根据购买足球节省的钱数购买篮球多花的钱数节余钱数,即可得出关于的一元一次方程,解之即可得出结论.
【详解】(1)解:设学校购买个足球,则购买个篮球,
根据题意得:,
解得:.
答:学校至多可购买个足球.
(2)根据题意得:
解得:.
答:的值为.
【点睛】本题考查了一元一次不等式的应用,一元一次方程的应用,根据题意列出不等式与方程是解题的关键.
17.(1)
(2)A,B两城各生产产品20件,80件
(3)
【分析】(1)利用待定系数法即可求出,的值;
(2)先根据(1)的结论得出与之间的函数关系,从而可得出,两城生产这批产品的总成本的和,据此建立方程求解即可;
(3)设从城运往C地的产品数量为件,, 两城总运费的和为,则从城运往地的产品数量为件,从城运往地的产品数量为件,从城运往地的产品数量为件,从而可得关于的不等式组,解得的范围,然后根据运费信息可得关于的一次函数,将的数值代入即可求得.
【详解】(1)解:由题意得:,
解得;
(2)解:设A城生产产品x件,则B城生产产品件,
由题意得,,
解得,
∴ ,
答:A,B两城各生产产品20件,80件;
(3)解:设从城运往C地的产品数量为件,, 两城总运费的和为,则从城运往地的产品数量为件,从城运往地的产品数量为件,从城运往地的产品数量为件,
由题意得:,
解得:,
∴,
整理得:,
当时,则,
∴P随n增大而减小,
∴当,P最小,最小值为,
又∵A,B两城总运费之和的最小值为150万元,
∴,
∴(舍去);
当时,,不符合题意;
当时,则,
∴P随n增大而增大,
∴当,P最小,最小值为,
又∵A,B两城总运费之和的最小值为150万元,
∴,
∴;
综上所述,.
【点睛】本题考查了一次函数在实际问题中的应用,一元一次不等式组的实际应用,理清题中的数量关系并明确一次函数的相关性质是解题的关键.
18.(1)①2.25;②
(2)
【分析】(1)①根据当时,即可求解;
②根据待定系数法求解即可;
(2)先求出调试①的抛物线解析式,然后令可求出求出,,然后比较大小即可.
【详解】(1)解:①当时,,
∴水管的长度是2.25m;
②把,;,;,,分别代入,
得,
解得,
∴
(2)解∶∵不改变喷水头的角度,将水管长度增加1m,
∴向上平移1个单位,
∴平移后的解析式为,即,
当时,,
解得,(不符合题意,舍去),
∴,
对于,
当时, ,
解得,(不符合题意,舍去)
∴,
∴.
【点睛】本题主要考查了二次函数的应用,待定系数法求函数关系式,解题的关键是读懂题意,列出函数关系式.
19.(1)
(2)不能得满分
(3)<
【分析】(1)设抛物线的表达式为,将代入解得a即可;
(2)令,解得x,与12.4m比较即可;
(3)令,解得x,根据(2)所得即可比较与.
【详解】(1)由题意,可知抛物线最高点的坐标为,
设抛物线的表达式为,
将代入,得,
解得.
∴第一次掷实心球时运动路线所在抛物线的表达式为;
(2)令,解得(负值已舍去),
∴实心球出手点与着陆点的水平距离为m.
∵,即,∴,
∴小军第一次投掷实心球不能得满分.
(3)∵,
解得(负值已舍去),
,,
,,
∴.
故答案为:<.
【点睛】本题考查二次函数的应用以及待定系数法求解析式,熟练掌握二次函数的性质是解题的关键.
20.(1)()
(2)米
(3)675000元
【分析】(1)过点作交于点,则四边形为矩形,由勾股定理求出,点的坐标为.再用待定系数法求解即可;
(2)根据当小车距离轴的垂直距离是2.5时,由,所以小车只可能在滑道上,令,代入(1)所求的函数解析式求解即可.
(3)令,代入(1)所求的函数解析式求解,得出点,设(),则点,则,,则所有支架的长度和,化简得,然后由二次函数最值求解即可.
【详解】(1)解:如解图,过点作交于点,
则四边形为矩形,
∴,,
∵,
∴,
在中,
∴点的坐标为.
∵抛物线的顶点为,
∴设抛物线的函数表达式为,代入点得,
解得,
∴滑道部分抛物线的函数表达式为();
(2)解:当小车距离轴的垂直距离是2.5时,
∵,
∴小车只可能在滑道上,
∴,解得:,(不合题意,舍去),
∴此时小车到出发点的水平距离为米;
(3)解:由题意得,,
令,解得(舍去),,即点,
设(),
∴点,则,,
∴所有支架的长度和,化简得,
∵,,
∴当时,有最大值,最大值为9,此时造价最高为元,
∴为了预算充足,至少要申请675000元资金.
【点睛】本题考查二次函数的应用,勾股定理,待定系数法求二次函数解析式,熟练掌握二次函数的图象性质、最值是解题的关键.
21.(1)
(2)该男生在此项考试中能得满分.
【分析】(1)已知顶点坐标为,设成顶点式,将代入求出a的值,即可求出函数表达式.
(2)根据(1)中的表达式,求出时x的值,即D点的坐标,则可知OD的长,再与9.7作比较,即可判断是否得满分.
【详解】(1)设
将代入得
解得
(2)当时,
(舍去)
∴该男生在此项考试中能得满分.
【点睛】本题主要考查了求二次函数表达式,及二次函数的实际应用,熟练掌握求二次函数表达式式是解题的关键.
22.(1)
(2)2450元
【分析】(1)直接利用待定系数法求解即可得;
(2)根据利润(销售单价成本价)销量,利用二次函数的性质求解即可得.
【详解】(1)解:设与的一次函数关系式为,
由题意得:,
解得:,
则与的一次函数关系式为.
(2)解:由题意得:
,
这个抛物线的对称轴为直线,且开口向下,
当时,取得最大值,最大值为2450,
答:该茶商这一周销售该品牌茶叶所获利润(元)的最大值为2450元.
【点睛】本题考查了一次函数的应用、二次函数的应用,熟练掌握待定系数法和二次函数的性质是解题关键.
23.(1)
(2)这种头盔月售价定为71元时,可获得月销售利润最大,最大月销售利润是1682元
【分析】(1)设与之间的函数关系式为,利用待定系数法求解即可;
(2)根据利润=(售价成本)×数量,得到关于的函数关系式,再利用二次函数的性质求解即可.
【详解】(1)解:设与之间的函数关系式为,
把,和,分别代入,得,
解得,,
与的函数关系式为;
(2)解:设这种头盔月销售利润为元,
由题意可得:,
,,
当时,有最大值.
(元).
答:这种头盔月售价定为71元时,可获得月销售利润最大,最大月销售利润是1682元.
【点睛】本题考查了销售问题的数量关系在解决实际问题时的运用,一次函数和二次函数的解析式的运用,解题的关键是根据题意建立函数关系.
24.(1)甲、乙两种商品的进货单价分别是10、15元/件
(2)
(3)甲商品的销售单价定为15元件时,日销售利润最大,最大利润是50元
【分析】(1)设甲、乙两种商品的进货单价分别是a元件、b元件,然后列出二元一次方程组并求解即可;
(2)设y与x之间的函数关系式为,用待定系数法求解即可;
(3)先列出利润和销售量的函数关系式,然后运用二次函数的性质求最值即可.
【详解】(1)解:设甲、乙两种商品的进货单价分别是a元件、b元件,由题意得:
,
解得:.
∴甲、乙两种商品的进货单价分别是10元件、15元件.
(2)设y与x之间的函数关系式为,将,代入得:
,
解得:.
∴y与x之间的函数关系式为.
(3)由题意得:
.
∴当时,w取得最大值50.
∴当甲商品的销售单价定为15元件时,日销售利润最大,最大利润是50元.
【点睛】本题考查了二元一次方程组的应用、运用待定系数法则求函数解析式以及二次函数的性质求最值等知识点,弄懂题意、列出方程组或函数解析式是解答本题的关键.
25.(1)
(2)当时,线上和线下销售月利润总和W达到最大,最大利润是6000元
(3)
【分析】(1)利用待定系数法求解即可;
(2)根据利润=(售价成本)×数量求出W关于x的二次函数关系式,利用二次函数的性质求解即可;
(3)先求出当时,x的值,然后根据(2)可知当时,W随x增大而增大,由此即可得到答案.
【详解】(1)解:设y与x之间的函数关系式为,
∴,
∴,
∴y与x之间的函数关系式为;
(2)解:由题意得
,
∵,
∴当时,W随x增大而增大,
∴当时,W最大,最大为6000,
∴当时,线上和线下销售月利润总和W达到最大,最大利润是6000元;
(3)解:当时,,
解得,
解得或,
由(2)得当时,W随x增大而增大,
∴要使(2)中月利润总和W不低于4400元,则.
【点睛】本题主要考查了二次函数的应用,正确理解题意列出二次函数解析式和方程是解题的关键.
26.(1)
(2)该农产品销售量有16天不超过60千克
(3)当月第30天,该农产品的销售额最大,最大销售额是480元
【分析】(1)根据函数图象中的数据,可以得到y与x之间的函数关系式,并写出x的取值范围即可;
(2)分别在两段函数上求出时,的值,即可得出结论;
(3)设当月第x天的销售额为w元,根据销售额等于单价乘以销售数量,列出二次函数解析式,利用二次函数的性质求最值即可得出结果.
【详解】(1)解:设,
由图象可知:点在函数图象上,点在函数图象上,
∴,,
解得:,,
∴;
(2)依题意:将代入中,得,
将代入中,得,
结合函数图象可知:当时,,
即:该农产品销售量有16天不超过60千克.
(3)设当月第x天的销售额为w元,
当时,,
∴当时,w取得最大值,此时,
当时,,
∴当时,w取得最大值,此时,
综上:当时,w取得最大值,此时,
答:当月第30天,该农产品的销售额最大,最大销售额是480元.
【点睛】本题考查一次函数的实际应用,二次函数的实际应用.正确的识图,准确的求出函数解析式,是解题的关键.
27.(1);
(2)3人.
(3)每天能获得的最大利润是180元,此时,每件服装的价格应定为55元.
【分析】(1)根据待定系数法,可得函数解析式;
(2)根据收入等于支出,可得一元一次方程,根据解一元一次方程,可得答案;
(3)分两种情况解答:①当时;②当时,依据:总利润=单件利润×销售量-工人工资及其他费用列出函数解析式,求解即可.
【详解】(1)解:(1)当时,设y与x的函数解析式为,由图象可得:,解得:.
∴;
当时,设y与x的函数解析式为,由图象得:
,解得:.
∴.
综上所述:y=.
(2)设人数为a,当时,,
则,
解得:.
答:该店员工人数为3.
(3)设每件服装的价格为元时,每天获得的利润为元.
当时
当时,最大值.
当时
当时,最大值=171.
∵
∴最大值
答:每天能获得的最大利润是180元,此时,每件服装的价格应定为55元.
【点睛】本题考查了二次函数的应用与一次函数和一元一次方程的应用能力,理解题意找到符合题意得相等关系函数解析式是解题的关键.
28.(1)
(2)3米
【分析】(1)题目中告知了抛物线的顶点,可以设抛物线的顶点式,又抛物线经过点即可求解顶点式中的,从而求解.
(2)设抛物线向后平移了米,用(1)中的顶点式,表示出新的抛物线解析式,将点坐标代入解析式中,求解即可.
【详解】(1)解:由题可知:当喷射出的水流距离喷水头8米时,达到最大高度5米,
则可设水流形成的抛物线为,
∴将点代入可得,
∴抛物线,
(2)解:设喷射架向左水平平移了m米,则平移后的抛物线可表示为,
将点代入得:,
解得或(舍去),
∴喷射架应向左水平移动3米.
【点睛】本题考查了二次函数实际问题中的应用,正确理解题意,熟练掌握待定系数法及二次函数性质是解题的关键.
29.(1)
(2)
(3)当为米时,造价最低,最低造价为2356000元
【分析】(1)设抛物线的函数表达式为,利用待定系数法即可求解;
(2)求得,推出,得到,据此即可求解;
(3)设,得到l关于a的二次函数,利用二次函数的性质即可求解.
【详解】(1)解:由题意可设抛物线的函数表达式为,
把代入,得:
,
解得:,
∴抛物线的函数表达式为;
(2)解:∵米,E点坐标为,
∴,
∵P和C到地面的距离均为n米,且P,C在抛物线上,
∴P,C关于直线对称.
∵C为两条形状完全相同的抛物线与的交点,
∴抛物线由抛物线向右平移20个单位得到,
∴,
∴,
将代入得
∴;
(3)解:∵,设,
则,,
∴
,
∵,
∴开口向上,
∴当时,最短,最短为23.56.
(元)
∴当为米时,造价最低,最低造价为2356000元.
【点睛】本题考查二次函数的应用以及平移的性质,关键用二次函数的性质解决实际问题.
30.(1);
(2),;
(3)
【分析】(1)由题意可知过点和点,且,代入解析式可求得解析式;
(2)两条抛物线的形状相同且顶点的纵坐标相同且经过点,设的解析式为,代入相关数据即可求得解析式,再根据题意进行取舍即可;
(3)无人机的横坐标为,根据题意列出不等式,求解即可.
【详解】(1)解:由已知可得:过点和点,设其解析式为,
代入两点,由的横坐标为可得,
,解得:,
故的解析式为:;
(2)解:两条抛物线的形状相同,
设的解析式为,
已知经过点,故的解析式为①,
顶点的纵坐标相同,
的顶点的横坐标为,代入①,
可得:,
解得:,
故的解析式为②或③,
由图可知的终点的横坐标小于0,而②中不合题意,故舍去②,
令将代入,
解得或(舍去),
故点的坐标为;
(3)解:由题意可得:,
解得:,
又,
解得:,
.
【点睛】本题考查二次函数的应用,根据题意正确求出函数的解析式是解题关键.
答案第32页,共33页
答案第33页,共33页
(2022秋 泰兴市期末)
1.一水果店售卖一种水果,以8元/千克的价格进货,经过往年销售经验可知:以12元/千克售卖,每天可卖60千克;若每千克涨价0.5元,每天要少卖2千克;若每千克降价0.5元,每天要多卖2千克,但不低于成本价.设该商品的价格为元/千克时,一天销售总质量为千克.
(1)求与的函数关系式.
(2)若水果店货源充足,每天以固定价格元/千克销售,试求出水果店每天利润与单价的函数关系式,并求出当为何值时,利润达到最大.
(2023 朝阳)
2.某超市以每件10元的价格购进一种文具,销售时该文具的销售单价不低于进价且不高于19元.经过市场调查发现,该文具的每天销售数量y(件)与销售单价x(元)之间满足一次函数关系,部分数据如下表所示:
销售单价x/元 … 12 13 14 …
每天销售数量y/元 … 36 34 32 …
(1)直接写出y与x之间的函数关系式;
(2)若该超市每天销售这种文具获利192元,则销售单价为多少元?
(3)设销售这种文具每天获利w(元),当销售单价为多少元时,每天获利最大?最大利润是多少元?
(2023 海淀区校级开学)
3.电缆在空中架设时,两端挂起的电缆下垂可以近似的看成抛物线的形状.如图,在一个斜坡上按水平距离间隔60米架设两个塔柱,每个塔柱固定电缆的位置离地面高度为27米(米),以过点A的水平线为x轴,水平线与电缆的另一个交点为原点O建立平面直角坐标系,如图所示.经测量,米,斜坡高度12米(即B、D两点的铅直高度差).
结合上面信息,回答问题:
(1)若以1米为一个单位长度,则D点坐标为_______,下垂电缆的抛物线表达式为_______.
(2)若电缆下垂的安全高度是13.5米,即电缆距离坡面铅直高度的最小值不小于13.5米时,符合安全要求,否则存在安全隐患.(说明:直线轴分别交直线和抛物线于点H、G.点G距离坡面的铅直高度为的长),请判断上述这种电缆的架设是否符合安全要求?请说明理由.
(2023春 江岸区校级月考)
4.如图,在斜坡底部点处安装一个的自动喷水装置,喷水头(视为点)的高度(喷水头距喷水装置底部的距离)是米,自动喷水装置喷射出的水流可以近似地看成抛物线.当喷射出的水流与喷水装置的水平距离为米时,达到最大高度米.以点为原点,自动喷水装置所在的直线为y轴,建立平面直角坐标系.
(1)求抛物线的解析式;
(2)斜坡上距离水平距离为米处有一棵高度为米的小树,垂直水平地面且点到水平地面的距离为米.
①记水流的高度为,斜坡的高度为,求的最大值(斜坡可视作直线OM);
②如果要使水流恰好喷射到小树顶端的点,直接写出自动喷水装置应向后平移(即抛物线向左)多少米?
(2023 武汉模拟)
5.如图,灌溉车为绿化带浇水,喷水口H离地竖直高度为1.2m.可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形,其水平宽度,竖直高度.下边缘抛物线是由上边缘抛物线向左平移得到,上边抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.4m,灌溉车到绿化带的距离为d(单位:m).
(1)求上边缘抛物线的函数解析式,并求喷出水的最大射程;
(2)求下边缘抛物线与x轴的正半轴交点B的坐标;
(3)要使灌溉车行驶时喷出的水能浇灌到整个绿化带,直接写出d的取值范围.
(2022秋 华容区期末)
6.农户销售某农产品,经市场调查发现:若售价为6元/千克,日销售量为40千克,若售价每提高1元/千克,日销售量就减少2千克.现设售价为元/千克(且为正整数).
(1)若某日销售量为24千克,求该日产品的单价;
(2)若政府将销售价格定为不超过18元/千克.设每日销售额为元,求关于的函数表达式,并求的最大值和最小值;
(3)市政府每日给农户补贴元后(为正整数),发现最大日收入(日收入=销售额+政府补贴)还是不超过450元,并且只有5种不同的单价使日收入不少于440元,请直接写出所有符合题意的的值.
(2023春 蔡甸区月考)
7.如图,抛物线,是某喷水器喷出的水抽象而成,抛物线由抛物线向左平移得到,把汽车横截面抽象为矩形,其中米,米,米,抛物线表达式为,,且点A,,,,均在坐标轴上.
(1)求抛物线表达式.
(2)求点的坐标.
(3)要使喷水器喷出的水能洒到整个汽车,记长为米,直接写出的取值范围.
(2022秋 华容区期末)
8.如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)运动员乙要抢到第二个落点D,他应再向前跑多少米 (取,)
(2023 淮安一模)
9.某网店销售一种文具袋,成本为30元/件,每天的销售量(件)与销售单价(元)之间满足一次函数关系,其图象如图所示.
(1)求与之间的函数关系式;
(2)如果规定每天的销量不低于240件,那么当销售单价为多少元时,每天获取的利润最大?最大利润是多少?
(2023 盘锦)
10.某工厂生产种产品,经市场调查发现,该产品每月的销售量y(件)与售价x(万元/件)之间满足一次函数关系.部分数据如下表:
每件售价x/万元 … 24 26 28 30 32 …
月销售量y/件 … 52 48 44 40 36 …
(1)求y与x的函数关系式(不写自变量的取值范围).
(2)该产品今年三月份的售价为35万元/件,利润为450万元.
①求:三月份每件产品的成本是多少万元?
②四月份工厂为了降低成本,提高产品质量,投资了450万元改进设备和革新技术,使每件产品的成本比三月份下降了14万元.若四月份每件产品的售价至少为25万元,且不高于30万元,求这个月获得的利润(万元)关于售价x(万元/件)的函数关系式,并求最少利润是多少万元?
(2023春 江都区月考)
11.某企业生产并销售某种产品,假设销售量与产量相等,图中的线段表示该产品每千克生产成本(单位:元)与产量x(单位:)之间的函数关系;线段表示该产品销售价(单位:元)与产量x(单位:)之间的函数关系,已知,.
(1)求线段所表示的与x之间的函数表达式;
(2)若,该产品产量为多少时,获得的利润最大?最大利润是多少?
(3)若,该产品产量为多少时,获得的利润最大?最大利润是多少?
(2023 梁溪区模拟)
12.为加强劳动教育,各校纷纷落实劳动实践基地.某校学生在种植某种高产番茄时,经过试验发现:①当每平方米种植2株番茄时,平均单株产量为8.4千克;②在每平方米种植的株数不超过10的前提下,以同样的栽培条件,株数每增加1株,平均单株产量减少0.8千克.
(1)求平均单株产量(千克)与每平方米种植的株数(为整数,且)之间的函数关系式;
(2)已知学校劳动基地共有10平方米的空地用于种植这种番茄.问:当每平方米种植多少株时,该学校劳动基地能获得最大的产量?最大产量为多少千克?
(2023春 仓山区校级期末)
13.根据以下素材,探索完成任务.
如何设计大棚苗木种植方案?
素材1:图1中有一个大棚苗木种植基地及其截面图,其下半部分是一个长为,宽为的矩形,其上半部分是一条抛物线,现测得,大棚顶部的最高点距离地面.
素材:种植苗木时,每棵苗木高,为了保证生长空间,相邻两棵苗木种植点之间间隔,苗木顶部不触碰大棚,且种植后苗木成轴对称分布.
(1)任务1:确定大棚上半部分形状.根据图2建立的平面直角坐标系,通过素材1提供的信息确定点的坐标,求出抛物线的函数关系式;
(2)任务2:探究种植范围.在图2的坐标系中,在不影响苗木生长的情况下,确定种植点的横坐标的取值范围.
(2023 岳麓区校级二模)
14.从2020年开始,越来越多的商家向线上转型发展,“直播带货”已经成为商家的一种促销的重要手段.某商家在直播间销售一种进价为每件10元的日用商品,经调查发现,该商品每天的销售量y(件)与销售单价x(元)满足,设销售这种商品每天的利润为W(元).
(1)求W与x之间的函数关系式;
(2)该商家每天想获得1250元的利润,又要减少库存,应将销售单价定为多少元?
(3)若销售单价不低于28元,且每天至少销售50件时,求W的最大值.
(2022秋 蜀山区校级期末)
15.某超市经销甲、乙两种商品.商品甲每千克成本为20元,经试销发现,该种商品每天销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系,商品乙的成本为4元/千克,销售单价为10元/千克,但每天供货总量只有80千克,且能当天销售完.为了让利消费者,超市开展了“买一送一”活动,即买1千克的商品甲,免费送1千克的商品乙.
(1)直接写出销售量y与销售单价x之间的函数表达式______;
(2)设这两种商品的每天销售总额为S元,求出S(元)与x(元/千克)的函数关系式:(注:商品的销售额销售单价销售量)
(3)设这两种商品销售总利润为W,若商品甲的售价不低于成本,不超过成本的,当销售单价定为多少时,才能使当天的销售总利润最大?最大利润是多少?
(注:销售总利润两种商品的销售总额两种商品的总成本)
(2023春 莲池区校级期中)
16.为促进学生德智体美劳全面发展,推动文化学习与体育锻炼协调发展,某校举办了学生趣味运动会.该校计划用不超过元购买足球和篮球共个,分别作为运动会团体一、二等奖的奖品.已知足球单价元,篮球单价元.
(1)学校至多可购买多少个足球?
(2)受卡塔尔世界杯的影响,学校商议决定按(1)问的结果购买足球作为一等奖奖品,以鼓励更多学生热爱足球,同时商场也对足球和篮球的价格进行调整,足球单价下降了,篮球单价上涨了,最终学校购买奖品的经费比计划经费的最大值节省了元,求的值.
(2023春 宜都市期末)
17.某公司分别在A,B两城生产同种产品,共100件.A城生产产品的总成本(万元)与产品数量(件)之间具有一次函数关系:.当时,;当时,.B城生产产品的每件成本为7万元.
(1)求,的值;
(2)当A,B两城生产这批产品的总成本之和为660万元时,求A,B两城各生产产品多少件?
(3)从A城把该产品运往C,D两地的费用分别为万元/件和3万元/件;从B城把该产品运往C,D两地的费用分别为1万元/件和2万元/件.C地需要90件,D地需要10件,在(2)的条件下,若A,B两城总运费之和的最小值为150万元,求的值.
(2023 海淀区校级四模)
18.某公园修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安装一个可调节角度的喷水头,从喷水头喷出的水柱形状是一条抛物线.建立如图所示的平面直角坐标系,抛物线形水柱的竖直高度(单位:m)与到池中心的水平距离(单位:m)满足的关系式近似为().
(1)在某次安装调试过程中,测得与的部分对应值如下表:
水平距离 0 0.5 1 1.5 2 2.5 3
竖直高度 2.25 2.8125 3 2.8125 2.25 1.3125 0
根据表格中的数据,解答下列问题:
①水管的长度是______m;
②求出与满足的函数解析式();
(2)安装工人在上述基础上进行了下面两种调试:
①不改变喷水头的角度,将水管长度增加1m,水柱落地时与池中心的距离为;
②不改变水管的长度,调节喷水头的角度,使得水柱满足,水柱落地时与池中心的距离为.则比较与的大小关系是:______(填“”或“”或“”)
(2023 罗山县三模)
19.实心球是中考体育项目之一.在掷实心球时,实心球被掷出后的运动路线可以看作是抛物线的一部分,已知小军在一次掷实心球训练中,第一次投掷时出手点距地面1.8m,实心球运动至最高点时距地面3.4m,距出手点的水平距离为4m.设实心球掷出后距地面的竖直高度为y(m),实心球距出手点的水平距离为x(m).如图,以水平方向为x轴,出手点所在竖直方向为y轴建立平面直角坐标系.
(1)求第一次掷实心球时运动路线所在抛物线的表达式.
(2)若实心球投掷成绩(即出手点与着陆点的水平距离)达到12.4m为满分,请判断小军第一次投掷实心球能否得满分.
(3)第二次投掷时,实心球运动的竖直高度y与水平距离x近似满足函数关系.记小军第一次投掷时出手点与着陆点的水平距离为,第二次投掷时出手点与着陆点的水平距离为,则______(填“>”“<”“=”).
(2023 花溪区校级一模)
20.过山车是一项富有刺激性的娱乐工具,在乘坐过山车的过程能够亲身体验由能量守恒、加速度和力交织在一起产生的效果,那感觉真是妙不可言.如图是合肥某乐园中部分过山车滑道所抽象出来的函数图象,线段是一段直线滑道,且长为米,点到地面距离米,点到地面距离米,滑道可以看作一段抛物线,最高点为.
(1)求滑道部分抛物线的函数表达式;
(2)当小车(看成点)沿滑道从运动到的过程中,小车距离轴的垂直距离为2.5米时,它到出发点的水平距离是多少?
(3)现在需要对滑道部分进行加固,建造某种材料的水平和竖直支架,,.已知这种材料的价格是75000元/米,为了预算充足,至少需要申请多少元的资金.
(2022秋 丰都县期末)
21.掷实心球是丰都中考体育考试项目之一,如图1是一名男生投实心球情境,实心球行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示、掷出时,起点处高度为1.9m,当水平距离为4m时,实心球行进至最高点3. 5m处.
(1)求y关于x的函数表达式:
(2)根据中考体育考试评分标准(男生版),投掷过程中,实心球从起点到落地点的水平距离大于等于9.7m时,即可得满分10分,该男生在此项考试中能否得满分,请说明理由.
(2022秋 建昌县期末)
22.2022年11月,“中国传统制茶技艺及其相关习俗”申遗成功,弘扬茶文化,倡导“和美雅静”的生活方式已成时尚.某茶商经销某品牌茶,成本为50元/千克,经市场调查发现,每周的销量(千克)与销售单价(元/千克)满足一次函数关系,部分数据列表如下:
销售单价(元/千克) 56 65 75 …
销量(千克) 128 110 90 …
(1)求与的一次函数关系式;
(2)求该茶商这一周销售该品牌茶叶所获利润(元)的最大值.
(2023 锦州二模)
23.近年来国家出台政策要求电动车上牌照,“保安全、戴头盔”出行.某头盔专卖店购进一批单价为36元的头盔,在销售中,通过分析销售情况发现这种头盔的月销售量(个)与售价(元/个)满足一次函数关系,表格是其中的两组对应值.
售价(元/个) … 50 55 …
月销售量(个) … 100 90 …
(1)求与之间的函数关系式;
(2)专卖店的优惠活动:若购买一个这种头盔,就赠送一个成本为6元的头盔面罩.请问这种头盔的售价定为多少元时,月销售利润最大,最大月销售利润是多少元?
(2023 金湖县三模)
24.某超市购进甲、乙两种商品,已知购进5件甲商品和2件乙商品,需80元;购进3件甲商品和4件乙商品,需90元.
销售单价x(元/件) 12 18
日销售量y(件) 16 4
(1)甲、乙两种商品的进货单价分别是多少?
(2)设甲商品的销售单价为x(单位:元/件),在销售过程中发现:当时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:
请写出当时,y与x之间的函数关系式.
(3)在(2)的条件下,设甲商品的日销售利润为w元,当甲商品的销售单价x(元件)定为多少时,日销售利润最大?最大利润是多少?
(2022秋 新抚区期末)
25.疫情防控常态化,全国人民同心抗疫.某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售,市场调查发现,线下的月销量y(件)与线下售价x(元/件,且)之间满足一次函数关系,部分数据如下表:
x(元/件) 12 13 14 15
y(件) 1000 900 800 700
(1)求y与x之间的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为600件.当x为何值时,线上和线下销售月利润总和W达到最大?最大利润是多少?
(3)要使(2)中月利润总和W不低于4400元,请直接写出x的取值范围.
(2023 嘉鱼县模拟)
26.为巩固扶贫攻坚成果,我县政府督查各部门和单位对口扶贫情况.某单位的帮扶对象种植的农产品在某月(按30天计)的第x天(x为正整数)的销售价格p(元/千克)关于x的函数关系为,销售量y(千克)与x之间的关系如图所示.
(1)直接写出y与x之间的函数关系式和x的取值范围;
(2)求该农产品的销售量有几天不超过60千克?
(3)当月第几天,该农产品的销售额最大,最大销售额是多少?(销售额=销售量×销售价格)
(2023 云梦县校级三模)
27.李丽大学毕业后回家乡创业,开了一家服装专卖店代理品牌服装的销售.已知该品牌服装进价每件40元,日销售(件)与销售价(元/件)之间的关系如图所示(实线),每天付员工的工资每人82元,每天应支付其他费用106元.
(1)直接写出日销售(件)与销售价(元/件)之间的函数关系式;
(2)当某天的销售价为48元/件时,收支恰好平衡(收入=支出),求该店员工人数;
(3)若该店只有2名员工,则每天能获得的最大利润是多少元 此时,每件服装的价格应定为多少元
(2023 卧龙区二模)
28.如图,在斜坡底部点O处安装一个自动喷水装置,喷水头(视为点A)的高度(喷水头距喷水装置底部的距离)是米,自动喷水装置喷射出的水流可以近似地看成抛物线.当喷射出的水流与喷水装置的水平距离为米时,达到最大高度米.以点O为原点,自动喷水装置所在的直线为y轴,建立平面直角坐标系.
(1)求抛物线的函数关系式;
(2)斜坡上距离O水平距离为米处有一棵高度为米的小树,垂直水平地面,且M点到水平地面的距离为2米,绿化工人向左水平移动喷水装置后,水流恰好喷射到小树顶端的点N,求自动喷水装置向左水平平移(即抛物线向左)了多少米?
(2023 竞秀区二模)
29.过山车是一项富有刺激性的娱乐工具,深受年轻游客的喜爱.某游乐场修建了一款大型过山车.如图所示,为这款过山车的一部分轨道(B为轨道最低点),它可以看成一段抛物线,其中米,米(轨道厚度忽略不计).
(1)求抛物线的函数表达式;
(2)在轨道上有两个位置P和C到地面的距离均为n米,当过山车运动到C处时,又进入下坡段(接口处轨道忽略不计,E为轨道最低点),已知轨道抛物线的形状与抛物线完全相同,E点坐标为,求n的值;
(3)现需要对轨道下坡段进行安全加固,建造某种材料的水平和竖直支架,且要求,已知这种材料的价格是100000元/米,请计算多长时,造价最低?最低造价为多少元?
(2023 利辛县模拟)
30.如图,某小区的景观池中安装一雕塑,米,喷出两股水流,两股水流可以抽象为平面直角坐标系中的两条抛物线(图中的,)的部分图象,两条抛物线的形状相同且顶点的纵坐标相同,且经测算发现抛物线的最高点(顶点)C距离水池面米,且与的水平距离为2米.
(1)求抛物线的解析式;
(2)求抛物线与x轴的交点B的坐标;
(3)小明同学打算操控微型无人机在,之间飞行,为了无人机的安全,要求无人机在竖直方向上的活动范围不小于米,设无人机与的水平距离为m,求m的取值范围.
试卷第2页,共14页
试卷第1页,共14页
参考答案:
1.(1)
(2),
【分析】(1)设该商品的价格为元/千克,根据“以12元/千克售卖,每天可卖60千克;若每千克涨价0.5元,每天要少卖2千克;若每千克降价0.5元,每天要多卖2千克,但不低于成本价”,得到销售总质量与的函数关系式.
(2)根据利润=每千克利润×销售总质量,得到有关利润的二次函数求最值即可;
【详解】(1)由题意可得,
(2)由题意可得,
当时,利润达到最大
答:当为时,利润达到最大
【点睛】本题主要考查了二次函数的应用,解题的关键是了解利润和售价,销售量之间的关系.
2.(1)
(2)18元
(3)19元,198元
【分析】(1)利用待定系数法求解即可;
(2)根据题意可列出关于x的一元二次方程,解出x的值,结合x的取值范围求解即可;
(3)根据题意可列出w与x的函数关系式,再根据二次函数的性质求解即可.
【详解】(1)解:设y与x之间的函数关系式为,由所给表格可知:
,解得:,
故y与x的函数关系式为;
(2)解:根据题意得:,
解得:.
又∵,
∴,
答:销售单价应为18元.
(3)解:,
∵,
∴抛物线开口向下.
∵对称轴为直线,
∴当时,w随x的增大而增大,
∴当时,w有最大值,.
答:当销售单价为19元时,每天获利最大,最大利润是198元.
【点睛】本题考查一次函数、二次函数的实际应用,一元二次方程的实际应用.理解题意,找出等量关系,列出等式是解题关键.
3.(1),
(2)这种电缆的架设符合安全要求,理由见解析
【分析】(1)由题意可求出米,米,即得出.又可求出米,即得出.结合,利用待定系数法求解即可;
(2)利用待定系数法可求出斜坡解析式为,即可求出电缆与坡面的铅直高度.再根据二次函数的性质求解即可.
【详解】(1)由题意得:米,米,米,米,轴,轴,
∴米,米,
∴.
∵米,
∴.
∵,
∴设下垂电缆的抛物线表达式为:,
∴,
解得:,
∴下垂电缆的抛物线表达式为:.
故答案为:,;
(2)这种电缆的架设符合安全要求,理由如下:
由(1)可知:,,,
设斜坡解析式为,
∴,解得:
∴斜坡解析式为,
则电缆与坡面的铅直高度.
∵,
∴当时,有最小值为18,即,
∴这种电缆的架设符合安全要求.
【点睛】本题考查二次函数的实际应用,一次函数的实际应用.理解题意,正确求出二次函数和一次函数解析式是解题关键.
4.(1)
(2)①最大值为;②喷射架应向后移动米
【分析】(1)根据当喷射出的水流距离喷水头米时,达到最大高度米,设设水流形成的抛物线为,代入点求出二次函数的解析式,即可求解;
(2)①先求出斜坡的高度的解析式,列出,把函数解析式化为顶点式,即可求解;
②设喷射架向后平移了米,设出平移后的函数解析式,代入点的坐标即可求解.
【详解】(1)解:由题可知:当喷射出的水流距离喷水头米时,达到最大高度米,
则可设水流形成的抛物线为 ,
将点代入可得,
∴抛物线为
(2)①解:由题可知点坐标为,
设直线的解析式为,
把点的坐标代入得
,
解得
则直线为
的最大值为.
②解:设喷射架向后平移了米,则平移后的抛物线可表示为
将点代入得:
解得或 舍去
喷射架应向后移动米.
【点睛】此题考查了二次函数在实际问题中的应用,根据题意求出函数的解析式是解决此题的关键.
5.(1);6m
(2)
(3)
【分析】(1)由顶点得,设,再根据抛物线过点,可得a的值,从而解决问题;
(2)由对称轴知点的对称点为,则下边缘抛物线是由上边缘抛物线向左平移4m得到的,可得点B的坐标;
(3)根据EF=0.5,求出点F的坐标,利用增减性可得d的最大值为最小值,从而得出答案.
【详解】(1)解:如图,由题意得是上边缘抛物线的顶点,
设,
又∵抛物线过点,∴,
∴,
∴上边缘抛物线的函数解析式为,当时,,
解得,(舍去),
∴喷出水的最大射程为6m;
(2)解:∵对称轴为直线,
∴点的对称点为,
∴下边缘抛物线是由上边缘抛物线向左平移4m得到的,
∴点B的坐标为;
(3)解:∵,
∴点F的纵坐标为0.5,
∴,解得,
∵,
∴,
当时,y随x的增大而减小,
∴当时,要使,
则 ,
∵当时,y随x的增大而增大,且时,,
∴当时,要使,则,
∵,灌溉车行驶时喷出的水能浇灌到整个绿化带,
∴d的最大值为,
再看下边缘抛物线,喷出的水能浇灌到绿化带底部的条件是,
∴d的最小值为2,
综上所述,d的取值范围是.
【点睛】本题是二次函数的实际应用,主要考查了待定系数法求二次函数解析式,二次函数的性质,二次函数与方程的关系等知识,读懂题意,建立二次函数模型是解题的关键.
6.(1)14
(2),最大338元,最小240元
(3)
【分析】(1) 售价为元/千克(且为正整数),则提价元,故销售量为千克,根据题意,列方程计算即可.
(2) 根据日销售额=日售价×日销售量,计算即可.
(3)由题意得:,由二次函数的对称性可知x的取值为11,12,13,14,15,从而计算可得a值.
【详解】(1)解:设产品售价为元/千克(且为正整数),则提价元,
故销售量为千克,
根据题意,得,
解得,
故该日产品的单价为14元/千克.
(2)解:设售价为元/千克(且为正整数),销售额为元,则提价元,
故销售量为千克,
∴,
∴,
∵,且对称轴右侧,y随x的增大而减小,到对称轴距离越大,函数值越小,且,
∴时,w取得最大值,且最大值为338元,
∴时,w取得最小值,且最小值为240元,
故,w的最大338元,w的最小240元.
(3)解:由题意得:,由二次函数的对称性可知x的取值为11,12,13,14,15,
∴时,元
∴时,元,
∴时,元,
且,
∴,
∵a是正整数,
∴a的值为.
【点睛】本题主要考查二次函数的应用.得到每天可售出的千克数是解决本题的突破点;本题需注意x的取值应为整数.解题的关键是熟练掌握待定系数法求函数解析式、根据销售额的相等关系列出函数解析式及二次函数的性质.
7.(1)
(2)
(3)
【分析】(1)分别把、点坐标代入解析式即可解答;
(2)由题意易得抛物线是由抛物线向左平移4米得到的,则有抛物线表达式为:,然后把代入求解即可;
(3)由(2)可得,又因为,即可解答
【详解】(1)解:把代入,得:
,
∵,
∴把代入,
解得,
抛物线表达式:,
当时,即,
解得:,
,,
抛物线表达式:;
(2)解:,
、的纵坐标为,
,
解得:,,
点的纵坐标是,
抛物线是由抛物线向左平移4米得到的,
抛物线表达式为:,
把代入,得:
,
解得,(舍去),
,
(3)解:由(2)可得点坐标为,,
,
由(1)得把代入,得,(舍去),
,,
,
【点睛】本题是二次函数的实际应用,主要考查了待定系数法求二次函数解析式,二次函数的性质,二次函数与方程的关系等知识,读懂题意,建立二次函数模型是解题的关键.
8.(1); (2)17米.
【分析】(1)易得第一次落地时抛物线的顶点,可设所求的函数解析式为顶点式,把(0,1)代入即可求得所求的函数解析式;
(2)易得第二次落地时的抛物线的二次项的系数与第一次落地时抛物线的二次项系数相同,顶点的纵坐标为第一个函数顶点纵坐标的一半,用顶点式设出所求的函数解析式,把C坐标代入后求得第二次落地时的抛物线解析式,让函数值等于0可得D的横坐标,减去OB的距离即为跑的距离.
【详解】(1)如图,设第一次落地时,抛物线的表达式为y=a(x-6)2+4.
由已知:当x=0时y=1.即1=36a+4,
∴a=-.
∴表达式为y=-(x-6)2+4=;
(2)由题意得:0=-(x-6)2+4
解得:x1=4+6≈13,x2=-4+6<0(舍去),
∴点C坐标为(13,0).
设第二次落地的抛物线为y=-(x-k)2+2.
将C点坐标代入得:0=-(13-k)2+2.
解得:k1=13-2<13(舍去),k2=13+2≈18.
∴y=-(x-18)2+2.
0=-(x-18)2+2.
x1=18-2(舍去),x2=18+2≈23,
∴BD=23-6=17(米).
答:运动员乙要抢到第二个落点D,他应再向前跑17米.
【点睛】本题考查了二次函数的应用;判断出两个二次函数的顶点坐标是解题的关键;用到的知识点为:若二次函数的形状相同,则两个二次函数的二次项系数相同.
9.(1)y=-10x+700; (2)当销售单价为46元时,每天利润最大,为3840元.
【分析】(1)利用待定系数法求解可得;
(2)根据“总利润每件利润销售量”列出函数解析式,并配方成顶点式,再结合的取值范围,利用二次函数的性质求解可得.
【详解】解:(1)设,
将、代入,得:,
解得:,
则;
(2)设每天获取的利润为,
则
,
又,
,
时,随的增大而增大,
当时,取得最大值,最大值为,
答:当销售单价为46元时,每天获取的利润最大,最大利润是3840元.
【点睛】本题主要考查了待定系数法求函数解析式及二次函数的应用,解题的关键是理解题意,找到题目蕴含的相等关系,并熟练掌握二次函数的性质求最大值.
10.(1)
(2)①20万元;②,950万元
【分析】(1)从表格中任选两组数据,利用待定系数法求解;
(2)利用(1)中结论求出3月份销量,根据利润、销量、成本、售价之间的关系列方程即可;②列关于x的二次函数关系式,结合自变量的取值范围求出函数的最值即可.
【详解】(1)解:设y与x的函数关系式为,将,代入,得:
,
解得,
y与x的函数关系式为;
(2)解:①将代入,得(件),
设三月份每件产品的成本是a万元,
由题意得,
解得,
即三月份每件产品的成本是20万元;
②四月份每件产品的成本比三月份下降了14万元,
四月份每件产品的成本为万元,
由题意得:,
,
抛物线的图象开口向下,
抛物线的对称轴为,,
时,取最小值,此时,
综上可知,关于售价x的函数关系式是,最少利润是950万元.
【点睛】本题考查一次函数、二次函数的实际应用,解题的关键是根据利润、销量、成本、售价之间的关系正确列出函数关系式.
11.(1)
(2),最大利润是1350元
(3),最大利润为1200元
【分析】(1)利用待定系数法直接求解即可;
(2)根据题意利用待定系数法可求出与x之间的函数表达式为.设获得的利润为w元,再根据利润=(销售价-成本)×产量可求出w与x的函数关系式,最后根据二次函数的性质求解即可;
(3)利用待定系数法可求出与x之间的函数表达式为,设获得的利润为元,则.又可求出,,即得出,即抛物线对称轴在y轴左侧,从而得出当时,随x的增大而增大,再根据二次函数的性质求解即可.
【详解】(1)设线段所表示的与x之间的函数表达式为,
将代入得:,
解得:,
∴线段所表示的与x之间的函数表达式为;
(2)若,设与x之间的函数表达式为,
根据题意得:,
解得:,
∴.
设获得的利润为w元,
根据题意得:,
∵,,
∴当时,w有最大值,最大值为1350元.
∴若,该产品产量为时,获得的利润最大,最大利润是1350元;
(3)设,由题意得:
,
解得:,
∴,
设获得的利润为元,
∴.
∵,
∴,,
∴,即抛物线对称轴在y轴左侧,
∴当时,随x的增大而增大,
∴当时,的值最大,元,
∴时,该产品产量为时,获得的利润最大,最大利润为1200元.
【点睛】本题主要考查待定系数求一次函数解析式及二次函数的实际应用能力,根据相等关系列出函数关系式,熟练根据二次函数的性质判断函数的最值情况是解题的关键.
12.(1)(,且为整数)
(2)6株,312千克
【分析】(1)根据题意,找出数量关系式,即可求出平均单株产量(千克)与每平方米种植的株数之间的函数关系式;
(2)利用总产量平均的产量种植的株数,列关于的一元二次方程,将其转化为顶点式,根据为整数,即可求出种多少株最大产量,以及最大产量多少.
【详解】(1)解:每平方米种植的株数每增加1株,单株产量减少0.8千克,
,
关于的函数表达式为(,且为整数);
故答案为:(,且为整数).
(2)解:设每平方米番茄产量为千克,
根据题意得:
,为整数,
当时,取最大值,最大值为,
(千克),
答:每平方米种植6株时,该学校劳动基地能获得最大的产量,最大产量为312千克.
【点睛】本题考查了一次函数和二次函数的综合运用,解题的关键需要找出和存在的关系,以及熟练掌握顶点式二次函数表达式.
13.(1)
(2)确定种植点的横坐标的取值范围为
【分析】(1)根据题意建立直角坐标系,分别得到,,,再根据待定系数法即可求出二次函数的解析式;
(2)根据每棵苗木高,且苗木顶部不触碰大棚得到,即可求出种植点的横坐标的取值范围;
【详解】(1)解:如下图所示,
根据题意得,,,,
设二次函数的解析式为,
得,
解方程组得,,
∴;
(2)当时,
得,
∴,
∴;
【点睛】本题考查二次函数的应用,解题的关键是根据题意求出抛物线的解析式.
14.(1),
(2)15元
(3)2160元
【分析】(1)利用利润等于单价利润乘以销售数量列出函数关系式即可;
(2)令,解一元二次方程即可;
(3)根据二次函数的性质,求最值即可.
【详解】(1)解:根据题意,有:,
化简,得:,
由题意:,解得:,
即函数关系为:,;
(2)令,可得:,
解得:,或者,
当时,销量:(件);
当时,销量:(件);
销量越高,越有利于减少库存,
即为了减少库存,将销售单价应定为15元;
(3)根据题意有:,解得:,
∵,,
∴当时,函数值随着x的增大而减小,
∵,
∴当时,函数值最大,最大为:.
答:此时W的最大值为2160元.
【点睛】本题考查二次函数的实际应用.读懂题意,正确的列出函数解析式,利用二次函数的性质进行求解,是解题的关键.
15.(1)
(2)
(3)当销售单价定为30元时,才能使当天的销售总利润最大,最大利润是240元
【分析】(1)利用待定系数法可求出一次函数的解析式;
(2)利用商品的销售额销售单价销售量,即可求出(元)与的函数关系式;
(3)利用销售总利润两种商品的销售总额两种商品的总成本求出两种商品销售总利润为W与销售单价之间的关系式,根据已知求出的取值范围,再将关系式化为配方式,然后根据二次函数的性质来进行计算即可.
【详解】(1)解:设与之间的函数表达式为,
将图象中、代入得:,解得:,
∴销售量y与销售单价x之间的函数表达式为:,
故答案为:;
(2)∵超市开展了“买一送一”活动,即买1千克的商品甲,免费送1千克的商品乙,且商品乙每天供货总量只有80千克,
∴商品甲的销量:,即,
∴,
则两种商品的每天销售总额:;
(3)两件商品的成本为:元,
∵商品甲的售价不低于成本,不超过成本的,,
∴,
,
即,
∵,
∴时,随的增大而增大,
∴时,的最大值,
答:当销售单价定为30元时,才能使当天的销售总利润最大,最大利润是240元.
【点睛】本题考查了待定系数法求一次函数的解析式和二次函数在实际问题中的应用,理清题中的数量关系是解题的关键.
16.(1)学校至多可购买个足球
(2)的值为
【分析】(1)设学校购买个足球,则购买个篮球,根据总价单价数量结合总费用不超过元,即可得出关于的一元一次不等式,解不等式即可得出结论;
(2)根据购买足球节省的钱数购买篮球多花的钱数节余钱数,即可得出关于的一元一次方程,解之即可得出结论.
【详解】(1)解:设学校购买个足球,则购买个篮球,
根据题意得:,
解得:.
答:学校至多可购买个足球.
(2)根据题意得:
解得:.
答:的值为.
【点睛】本题考查了一元一次不等式的应用,一元一次方程的应用,根据题意列出不等式与方程是解题的关键.
17.(1)
(2)A,B两城各生产产品20件,80件
(3)
【分析】(1)利用待定系数法即可求出,的值;
(2)先根据(1)的结论得出与之间的函数关系,从而可得出,两城生产这批产品的总成本的和,据此建立方程求解即可;
(3)设从城运往C地的产品数量为件,, 两城总运费的和为,则从城运往地的产品数量为件,从城运往地的产品数量为件,从城运往地的产品数量为件,从而可得关于的不等式组,解得的范围,然后根据运费信息可得关于的一次函数,将的数值代入即可求得.
【详解】(1)解:由题意得:,
解得;
(2)解:设A城生产产品x件,则B城生产产品件,
由题意得,,
解得,
∴ ,
答:A,B两城各生产产品20件,80件;
(3)解:设从城运往C地的产品数量为件,, 两城总运费的和为,则从城运往地的产品数量为件,从城运往地的产品数量为件,从城运往地的产品数量为件,
由题意得:,
解得:,
∴,
整理得:,
当时,则,
∴P随n增大而减小,
∴当,P最小,最小值为,
又∵A,B两城总运费之和的最小值为150万元,
∴,
∴(舍去);
当时,,不符合题意;
当时,则,
∴P随n增大而增大,
∴当,P最小,最小值为,
又∵A,B两城总运费之和的最小值为150万元,
∴,
∴;
综上所述,.
【点睛】本题考查了一次函数在实际问题中的应用,一元一次不等式组的实际应用,理清题中的数量关系并明确一次函数的相关性质是解题的关键.
18.(1)①2.25;②
(2)
【分析】(1)①根据当时,即可求解;
②根据待定系数法求解即可;
(2)先求出调试①的抛物线解析式,然后令可求出求出,,然后比较大小即可.
【详解】(1)解:①当时,,
∴水管的长度是2.25m;
②把,;,;,,分别代入,
得,
解得,
∴
(2)解∶∵不改变喷水头的角度,将水管长度增加1m,
∴向上平移1个单位,
∴平移后的解析式为,即,
当时,,
解得,(不符合题意,舍去),
∴,
对于,
当时, ,
解得,(不符合题意,舍去)
∴,
∴.
【点睛】本题主要考查了二次函数的应用,待定系数法求函数关系式,解题的关键是读懂题意,列出函数关系式.
19.(1)
(2)不能得满分
(3)<
【分析】(1)设抛物线的表达式为,将代入解得a即可;
(2)令,解得x,与12.4m比较即可;
(3)令,解得x,根据(2)所得即可比较与.
【详解】(1)由题意,可知抛物线最高点的坐标为,
设抛物线的表达式为,
将代入,得,
解得.
∴第一次掷实心球时运动路线所在抛物线的表达式为;
(2)令,解得(负值已舍去),
∴实心球出手点与着陆点的水平距离为m.
∵,即,∴,
∴小军第一次投掷实心球不能得满分.
(3)∵,
解得(负值已舍去),
,,
,,
∴.
故答案为:<.
【点睛】本题考查二次函数的应用以及待定系数法求解析式,熟练掌握二次函数的性质是解题的关键.
20.(1)()
(2)米
(3)675000元
【分析】(1)过点作交于点,则四边形为矩形,由勾股定理求出,点的坐标为.再用待定系数法求解即可;
(2)根据当小车距离轴的垂直距离是2.5时,由,所以小车只可能在滑道上,令,代入(1)所求的函数解析式求解即可.
(3)令,代入(1)所求的函数解析式求解,得出点,设(),则点,则,,则所有支架的长度和,化简得,然后由二次函数最值求解即可.
【详解】(1)解:如解图,过点作交于点,
则四边形为矩形,
∴,,
∵,
∴,
在中,
∴点的坐标为.
∵抛物线的顶点为,
∴设抛物线的函数表达式为,代入点得,
解得,
∴滑道部分抛物线的函数表达式为();
(2)解:当小车距离轴的垂直距离是2.5时,
∵,
∴小车只可能在滑道上,
∴,解得:,(不合题意,舍去),
∴此时小车到出发点的水平距离为米;
(3)解:由题意得,,
令,解得(舍去),,即点,
设(),
∴点,则,,
∴所有支架的长度和,化简得,
∵,,
∴当时,有最大值,最大值为9,此时造价最高为元,
∴为了预算充足,至少要申请675000元资金.
【点睛】本题考查二次函数的应用,勾股定理,待定系数法求二次函数解析式,熟练掌握二次函数的图象性质、最值是解题的关键.
21.(1)
(2)该男生在此项考试中能得满分.
【分析】(1)已知顶点坐标为,设成顶点式,将代入求出a的值,即可求出函数表达式.
(2)根据(1)中的表达式,求出时x的值,即D点的坐标,则可知OD的长,再与9.7作比较,即可判断是否得满分.
【详解】(1)设
将代入得
解得
(2)当时,
(舍去)
∴该男生在此项考试中能得满分.
【点睛】本题主要考查了求二次函数表达式,及二次函数的实际应用,熟练掌握求二次函数表达式式是解题的关键.
22.(1)
(2)2450元
【分析】(1)直接利用待定系数法求解即可得;
(2)根据利润(销售单价成本价)销量,利用二次函数的性质求解即可得.
【详解】(1)解:设与的一次函数关系式为,
由题意得:,
解得:,
则与的一次函数关系式为.
(2)解:由题意得:
,
这个抛物线的对称轴为直线,且开口向下,
当时,取得最大值,最大值为2450,
答:该茶商这一周销售该品牌茶叶所获利润(元)的最大值为2450元.
【点睛】本题考查了一次函数的应用、二次函数的应用,熟练掌握待定系数法和二次函数的性质是解题关键.
23.(1)
(2)这种头盔月售价定为71元时,可获得月销售利润最大,最大月销售利润是1682元
【分析】(1)设与之间的函数关系式为,利用待定系数法求解即可;
(2)根据利润=(售价成本)×数量,得到关于的函数关系式,再利用二次函数的性质求解即可.
【详解】(1)解:设与之间的函数关系式为,
把,和,分别代入,得,
解得,,
与的函数关系式为;
(2)解:设这种头盔月销售利润为元,
由题意可得:,
,,
当时,有最大值.
(元).
答:这种头盔月售价定为71元时,可获得月销售利润最大,最大月销售利润是1682元.
【点睛】本题考查了销售问题的数量关系在解决实际问题时的运用,一次函数和二次函数的解析式的运用,解题的关键是根据题意建立函数关系.
24.(1)甲、乙两种商品的进货单价分别是10、15元/件
(2)
(3)甲商品的销售单价定为15元件时,日销售利润最大,最大利润是50元
【分析】(1)设甲、乙两种商品的进货单价分别是a元件、b元件,然后列出二元一次方程组并求解即可;
(2)设y与x之间的函数关系式为,用待定系数法求解即可;
(3)先列出利润和销售量的函数关系式,然后运用二次函数的性质求最值即可.
【详解】(1)解:设甲、乙两种商品的进货单价分别是a元件、b元件,由题意得:
,
解得:.
∴甲、乙两种商品的进货单价分别是10元件、15元件.
(2)设y与x之间的函数关系式为,将,代入得:
,
解得:.
∴y与x之间的函数关系式为.
(3)由题意得:
.
∴当时,w取得最大值50.
∴当甲商品的销售单价定为15元件时,日销售利润最大,最大利润是50元.
【点睛】本题考查了二元一次方程组的应用、运用待定系数法则求函数解析式以及二次函数的性质求最值等知识点,弄懂题意、列出方程组或函数解析式是解答本题的关键.
25.(1)
(2)当时,线上和线下销售月利润总和W达到最大,最大利润是6000元
(3)
【分析】(1)利用待定系数法求解即可;
(2)根据利润=(售价成本)×数量求出W关于x的二次函数关系式,利用二次函数的性质求解即可;
(3)先求出当时,x的值,然后根据(2)可知当时,W随x增大而增大,由此即可得到答案.
【详解】(1)解:设y与x之间的函数关系式为,
∴,
∴,
∴y与x之间的函数关系式为;
(2)解:由题意得
,
∵,
∴当时,W随x增大而增大,
∴当时,W最大,最大为6000,
∴当时,线上和线下销售月利润总和W达到最大,最大利润是6000元;
(3)解:当时,,
解得,
解得或,
由(2)得当时,W随x增大而增大,
∴要使(2)中月利润总和W不低于4400元,则.
【点睛】本题主要考查了二次函数的应用,正确理解题意列出二次函数解析式和方程是解题的关键.
26.(1)
(2)该农产品销售量有16天不超过60千克
(3)当月第30天,该农产品的销售额最大,最大销售额是480元
【分析】(1)根据函数图象中的数据,可以得到y与x之间的函数关系式,并写出x的取值范围即可;
(2)分别在两段函数上求出时,的值,即可得出结论;
(3)设当月第x天的销售额为w元,根据销售额等于单价乘以销售数量,列出二次函数解析式,利用二次函数的性质求最值即可得出结果.
【详解】(1)解:设,
由图象可知:点在函数图象上,点在函数图象上,
∴,,
解得:,,
∴;
(2)依题意:将代入中,得,
将代入中,得,
结合函数图象可知:当时,,
即:该农产品销售量有16天不超过60千克.
(3)设当月第x天的销售额为w元,
当时,,
∴当时,w取得最大值,此时,
当时,,
∴当时,w取得最大值,此时,
综上:当时,w取得最大值,此时,
答:当月第30天,该农产品的销售额最大,最大销售额是480元.
【点睛】本题考查一次函数的实际应用,二次函数的实际应用.正确的识图,准确的求出函数解析式,是解题的关键.
27.(1);
(2)3人.
(3)每天能获得的最大利润是180元,此时,每件服装的价格应定为55元.
【分析】(1)根据待定系数法,可得函数解析式;
(2)根据收入等于支出,可得一元一次方程,根据解一元一次方程,可得答案;
(3)分两种情况解答:①当时;②当时,依据:总利润=单件利润×销售量-工人工资及其他费用列出函数解析式,求解即可.
【详解】(1)解:(1)当时,设y与x的函数解析式为,由图象可得:,解得:.
∴;
当时,设y与x的函数解析式为,由图象得:
,解得:.
∴.
综上所述:y=.
(2)设人数为a,当时,,
则,
解得:.
答:该店员工人数为3.
(3)设每件服装的价格为元时,每天获得的利润为元.
当时
当时,最大值.
当时
当时,最大值=171.
∵
∴最大值
答:每天能获得的最大利润是180元,此时,每件服装的价格应定为55元.
【点睛】本题考查了二次函数的应用与一次函数和一元一次方程的应用能力,理解题意找到符合题意得相等关系函数解析式是解题的关键.
28.(1)
(2)3米
【分析】(1)题目中告知了抛物线的顶点,可以设抛物线的顶点式,又抛物线经过点即可求解顶点式中的,从而求解.
(2)设抛物线向后平移了米,用(1)中的顶点式,表示出新的抛物线解析式,将点坐标代入解析式中,求解即可.
【详解】(1)解:由题可知:当喷射出的水流距离喷水头8米时,达到最大高度5米,
则可设水流形成的抛物线为,
∴将点代入可得,
∴抛物线,
(2)解:设喷射架向左水平平移了m米,则平移后的抛物线可表示为,
将点代入得:,
解得或(舍去),
∴喷射架应向左水平移动3米.
【点睛】本题考查了二次函数实际问题中的应用,正确理解题意,熟练掌握待定系数法及二次函数性质是解题的关键.
29.(1)
(2)
(3)当为米时,造价最低,最低造价为2356000元
【分析】(1)设抛物线的函数表达式为,利用待定系数法即可求解;
(2)求得,推出,得到,据此即可求解;
(3)设,得到l关于a的二次函数,利用二次函数的性质即可求解.
【详解】(1)解:由题意可设抛物线的函数表达式为,
把代入,得:
,
解得:,
∴抛物线的函数表达式为;
(2)解:∵米,E点坐标为,
∴,
∵P和C到地面的距离均为n米,且P,C在抛物线上,
∴P,C关于直线对称.
∵C为两条形状完全相同的抛物线与的交点,
∴抛物线由抛物线向右平移20个单位得到,
∴,
∴,
将代入得
∴;
(3)解:∵,设,
则,,
∴
,
∵,
∴开口向上,
∴当时,最短,最短为23.56.
(元)
∴当为米时,造价最低,最低造价为2356000元.
【点睛】本题考查二次函数的应用以及平移的性质,关键用二次函数的性质解决实际问题.
30.(1);
(2),;
(3)
【分析】(1)由题意可知过点和点,且,代入解析式可求得解析式;
(2)两条抛物线的形状相同且顶点的纵坐标相同且经过点,设的解析式为,代入相关数据即可求得解析式,再根据题意进行取舍即可;
(3)无人机的横坐标为,根据题意列出不等式,求解即可.
【详解】(1)解:由已知可得:过点和点,设其解析式为,
代入两点,由的横坐标为可得,
,解得:,
故的解析式为:;
(2)解:两条抛物线的形状相同,
设的解析式为,
已知经过点,故的解析式为①,
顶点的纵坐标相同,
的顶点的横坐标为,代入①,
可得:,
解得:,
故的解析式为②或③,
由图可知的终点的横坐标小于0,而②中不合题意,故舍去②,
令将代入,
解得或(舍去),
故点的坐标为;
(3)解:由题意可得:,
解得:,
又,
解得:,
.
【点睛】本题考查二次函数的应用,根据题意正确求出函数的解析式是解题关键.
答案第32页,共33页
答案第33页,共33页
同课章节目录
