第二十三章 专题01与旋转有关的计算(30题)(含解析)2023-2024学年九年级数学上册人教版
文档属性
| 名称 | 第二十三章 专题01与旋转有关的计算(30题)(含解析)2023-2024学年九年级数学上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-05 23:14:15 | ||
图片预览




文档简介
专题第01讲 与旋转有关的计算
(2023春 秦都区期末)
1.如图,是等边三角形,点 E在边上,连接,将绕点 B逆时针旋转60°得到,连接 .
(1)求证:;
(2)若,求的周长.
(2023春 北林区期末)
2.如图,在正方形ABCD中,E,F是对角线BD上两点,且,将绕点A顺时针旋转后,得到,连接.
(1)求证:;
(2)求证:.
(2022秋 同心县期末)
3.如图,是等边三角形,点在边上,将绕点旋转得到.
(1)求证:是等边三角形
(2)若,求的周长.
(2023春 清远期末)
4.如图,在中,点在边上,,将线段绕点旋转到的位置,使得,连接,与交于点.
(1)求证:;
(2)若,,求的度数.
(2023春 白银期中)
5.如图,在四边形中,,,,点在对角线上,将线段绕点顺时针旋转,得到线段,连接.
(1)求证:;
(2)若,求证:.
(2023春 南城县期中)
6.如图,点O是等边三角形内一点,将绕点C顺时针旋转得到,连接.
(1)求证:;
(2)若,,,求的度数.
(2023春 罗源县校级期中)
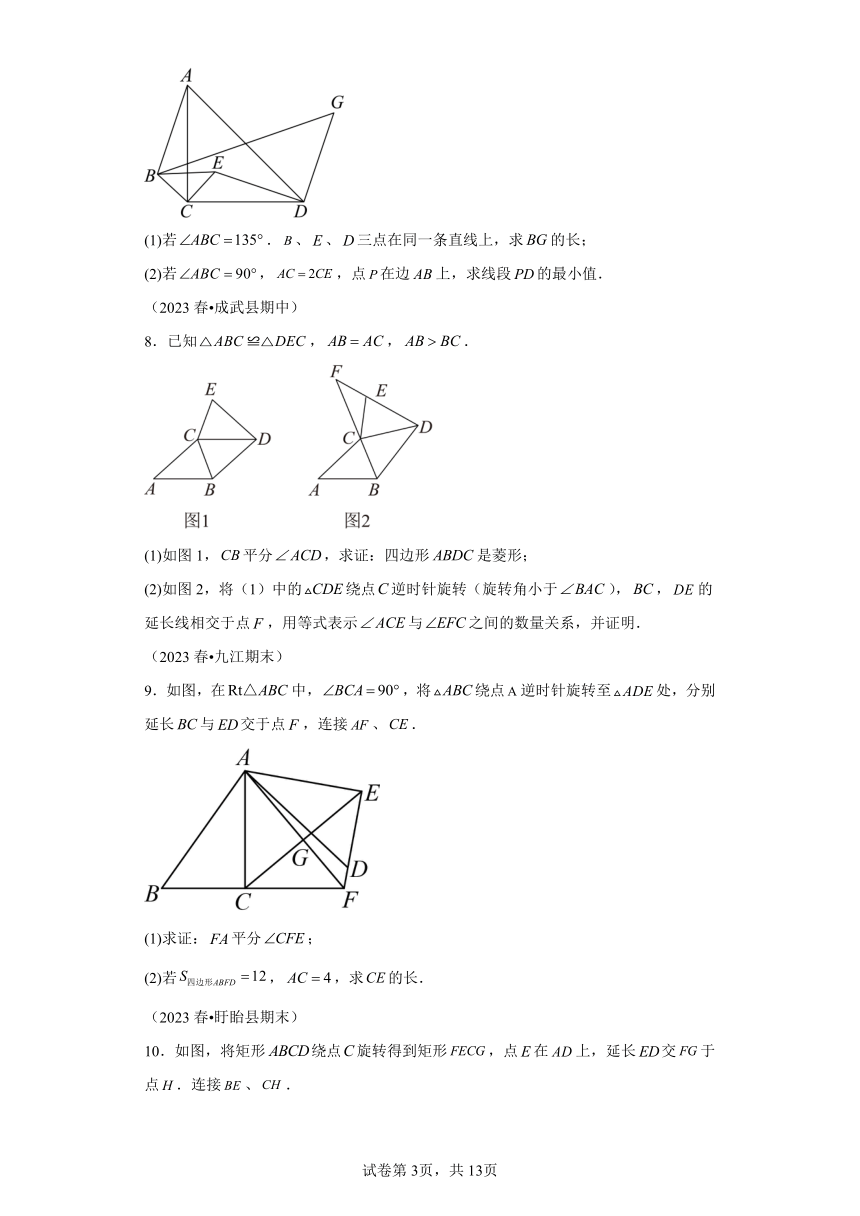
7.如图,先将绕点顺时针旋转得到,再将线段绕点顺时针旋转得到,连接、、,且.
(1)若.、、三点在同一条直线上,求的长;
(2)若,,点在边上,求线段的最小值.
(2023春 成武县期中)
8.已知,,.
(1)如图1,平分,求证:四边形是菱形;
(2)如图2,将(1)中的绕点逆时针旋转(旋转角小于),,的延长线相交于点,用等式表示与之间的数量关系,并证明.
(2023春 九江期末)
9.如图,在中,,将绕点逆时针旋转至处,分别延长与交于点,连接、.
(1)求证:平分;
(2)若,,求的长.
(2023春 盱眙县期末)
10.如图,将矩形绕点旋转得到矩形,点在上,延长交于点.连接、.
(1)四边形是怎样的特殊四边形?证明你的结论;
(2)若长为2,则的长为 时,四边形为菱形.
(2023春 平山县期末)
11.如图,PQ∥MN,A、B分别为直线MN、PQ上两点,且∠BAN=45°,若射线AM绕点A顺时针旋转至AN后立即回转,射线BQ绕点B逆时针旋转至BP后立即回转,两射线分别绕点A、点B不停地旋转,若射线AM转动的速度是a°/秒,射线BQ转动的速度是b°/秒,且a、b满足|a﹣5|+(b﹣1)2=0.(友情提醒:钟表指针走动的方向为顺时针方向)
(1)a= ,b= ;
(2)若射线AM、射线BQ同时旋转,问至少旋转多少秒时,射线AM、射线BQ互相垂直.
(3)若射线AM绕点A顺时针先转动18秒,射线BQ才开始绕点B逆时针旋转,在射线BQ到达BA之前,问射线AM再转动多少秒时,射线AM、射线BQ互相平行?
(2023春 振兴区校级期中)
12.如图(1),在中,,,射线于点,动点从点出发沿射线方向运动;以每秒1个单位长度的速度运动,运动时间为秒;
(1)以点为旋转中心,将逆时针旋转,得到线段,连接,是否存在最小值,不存在,则说明理由,存在则求出最小时的值及的最小值;
(2)若射线为的平分线,当点从点出发时,点从点向点与点同时同速运动,连接交于点,当为等腰三角形时,直接写出所有可能的t值.
(2023春 迁安市期中)
13.老师在黑板上出示题目:
如图,在中,,线段与CB边重合,从现在的位置绕着点C按逆时针方向旋转一周回到原来的位置是否有一位置使 如果有这样的位置,请画出示意图,并求出的度数,如果没有说明理由?
(1)嘉嘉认为:有这样一个位置,使得,如图.请你按照嘉嘉的做法,求出的度数.
(2)琪琪认为:嘉嘉的想法不全面,还存在另外一种情况使得你是否同意琪琪的说法?如果同意,请画出图形,并求出此时的度数;如果不同意,请说明理由.
(2022秋 青山湖区期末)
14.阅读下面材料,并解决问题:
(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=__________;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
(2023春 清江浦区期末)
15.如图1,,点在直线上,点在直线上,射线绕点顺时针从射线旋转至射线后便立即回转;射线绕点顺时针从射线旋转至射线后便立即回转:射线、射线不停地来回旋转.若射线转动的速度是度秒,射线转动的速度是度秒,且、是方程的正整数解.
(1) , ;
(2)如图2,若,两条射线同时转动,在射线到达之前,若两条射线交于点,过作交于,若,求的度数;
(3)若射线先转动30秒,射线才开始转动,在射线到达之前,射线转动几秒,射线与射线互相平行?
(2023春 蒸湘区期末)
16.如图,有一副直角三角板如图1放置(其中),与直线重合,且三角板,三角板均可以绕点P逆时针旋转.
(1)在图1中, ;
(2)①如图2,若三角板保持不动,三角板绕点P逆时针旋转,转速为秒,转动一周三角板就停止转动,在旋转的过程中,当旋转时间为多少时,有成立;
②如图3,在图1基础上,若三角板的边从处开始绕点P逆时针旋转,转速为秒,同时三角板的边从处开始绕点P逆时针旋转,转速为秒,当转到与重合时,两三角板都停止转动,在旋转过程中,当时,求旋转的时间是多少?
(2023春 雄县期中)
17.教材中有这样一道题:如图1,四边形是正方形,是上的任意一点,于点,,且交于点.求证:.
小明通过证明解决了问题,在此基础上他进一步提出了以下以下回题,请你解答.
(1)若图1中的点为延长线上一点,其余条件不变,如图2所示,猜想此时,,之间的数量关系,并证明你的结论.
(2)将图1中的绕点逆时针旋转,使得与重合,记此时点的对应点为点,如图3所示,若正方形的边长为3,求的长度.
(2023春 长垣市期末)
18.综合与实践
数学社团的同学以“两条平行线,和一块含角的直角三角尺”为主题开展数学活动,已知点E,F不可能同时落在直线和之间.
探究:(1)如图1,把三角尺的角的顶点E,G分别放在,上,若,求的度数;
类比:(2)如图2,把三角尺的锐角顶点G放在上,且保持不动,若点E恰好落在和之间,且与所夹锐角为,求的度数;
迁移:(3)把三角尺的锐角顶点G放在上,且保持不动,旋转三角尺,若存在,直接写出射线与所夹锐角的度数.
(2023春 阳城县期末)
19.如图1,将一副直角三角板放在同一条直线上,其中,.
(1)观察猜想:将图1中的三角尺沿的方向平移至图2的位置,使得点O与点N重合,与相交于点E,则 ;
(2)操作探究:将图1中的三角尺绕点O按顺时针方向旋转,使一边在的内部,如图3,且OD恰好平分,与相交于点E,求的度数;
(3)深化拓展:将图1中的三角尺绕点O按沿顺时针方向旋转一周,在旋转的过程中,当边旋转多少度时,边恰好与边平行?
(2023春 岱岳区期末)
20.知识探究:如图1,点E是正方形对角线AC上任意一点,以点E为直角顶点的直角两边,分别角与,相交于M点,N点.当时,请探究与的数量关系,并说明理由;
拓展探究:当绕点E顺时针旋转到点M与点D重合时,如图2,请探究与的数量关系,并说明理由;
迁移运用:在图2的基础上,过点E作于点H,如图3,证明H是线段的中点.
(2023春 顺平县期末)
21.如图,正方形的对角线相交于点O,点O又是正方形的一个顶点,且这两个正方形边长相等.与相交于点M,与相交于点N.
(1)求证:;
(2)嘉琪说:当正方形绕点O转动,且与垂直时,四边形的面积最小.你同意嘉琪的说法吗?请说明理由;
(3)若正方形的边长为a,用含a的代数式表示两个正方形重叠部分的面积为______.
(2023春 沈丘县期末)
22.如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE=______;
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
(2023春 东昌府区期末)
23.在等边三角形的内部有一点,连接,,以点为中心,把逆时针旋转得到,连接,.以点为中心,把顺时针旋转得到,连接,.
(1)判断和的大小关系,并说明理由;
(2)求证:;
(3)求证:四边形是平行四边形.
(2022秋 河口区期末)
24.感知:如图①,和都是等腰直角三角形,,点在线段上,点在线段上,我们很容易得到,不需证明.
探究:如图②,将绕点逆时针旋转,连结和,此时是否依然成立?若成立,写出证明过程;若不成立,说明理由.
应用:如图③,当绕点逆时针旋转,使得点落在的延长线上,连结.
①的度数为______度;
②若,,则线段的长为______.
(2023春 内乡县期末)
25.将一副直角三角板如图1,摆放在直线MN上(直角三角板和直角三角板,,,,),保持三角板不动,将三角板绕点以每秒的速度顺时针旋转,旋转时间为秒,当与射线重合时停止旋转.
(1)如图2,当为的角平分线时,求此时t的值;
(2)当旋转至的内部时,求与的数量关系;
(3)在旋转过程中,当三角板的其中一边平行于三角板的某一边时,求此时t等于 (直接写出答案即可).
(2023春 衡山县期末)
26.一副三角板如图1摆放,,,,点在上,点在上,且平分,现将三角板绕点以每秒的速度顺时针旋转(当点落在射线上时停止旋转),设旋转时间为秒.
(1)当 秒时,;当 秒时,;
(2)在旋转过程中,与的交点记为,如图2,若有两个内角相等,求t的值;
(3)当边与边、分别交于点、时,如图3,连接,设,,,试问是否为定值?若是,请求出定值;若不是,请说明理由.
(2023春 太原期中)
27.如图,已知中,,,点是平面内一点,将线段绕点按逆时针方向旋转得到线段.
(1)当点D在内部时,连接,.请判断线段与的数量关系,并说明理由;
(2)请从A,B两题中任选一题作答.
A.当点D在内部时,若直线恰好经过点B,直接写出的度数.
B.当点D在外部时,若直线恰好经过点C,直接写出的度数.
(2023春 遂平县期末)
28.如图1,将一副三角板的直角重合放置,其中∠A=30°,∠CDE=45°.
(1)如图1,求∠EFB的度数;
(2)若三角板ACB的位置保持不动,将三角板CDE绕其直角顶点C顺时针方向旋转.
①当旋转至如图2所示位置时,恰好CD∥AB,则∠ECB的度数为 ;
②若将三角板CDE继续绕点C旋转,直至回到图1位置.在这一过程中,是否还会存在△CDE其中一边与AB平行?如果存在,请你画出示意图,并直接写出相应的∠ECB的大小;如果不存在,请说明理由.
(2023 碑林区校级模拟)
29.似曾相识
(1)如图①,正方形的边长等于4,中心为,正方形的边长也等于4,在正方形绕着点O旋转的过程中,若将这两个正方形重叠部分的面积记为S,那么S是否为定值?若S为定值,请直接写出该定值;若S变化,请直接写出它的变化范围.
类比探索
(2)如图②,等边的边长等于4,中心为,等边的边长也等于4,在等边绕着点O旋转的过程中,若将这两个等边三角形重叠部分的面积记为S,那么S是否为定值?若S为定值,请直接写出该定值;若S变化,请求出它的变化范围.
(2023 青山湖区模拟)
30.●问题发现
如图1,和都是等边三角形,边和在同一直线上,是边的中点,,连接,则下列结论正确的是__________.(填序号即可)
①;②;③;④整个图形是轴对称图形.
●数学思考
将图1中的绕着点旋转,不动,连接和,如图2,则和具有怎样的数量和位置关系?请给出证明过程;
●拓展应用
已知,,在图1中的绕着点旋转的过程中,当时,求线段的长度.
试卷第2页,共3页
试卷第1页,共3页
参考答案:
1.(1)详见解析
(2)
【分析】(1)利用等边三角形的性质和判定和旋转的性质,证明,即可得解;
(2)由,结合(1)的结论,等线段转化,得到的周长.
【详解】(1)证明:∵是等边三角形,
∴.
∵是由 绕点 B逆时针旋转 60°得到,
∴,
∴是等边三角形,
∴
∴,
∴;
(2)∵和都是等边三角形,
∴
∴的周长为.
【点睛】本题考查了旋转的性质及等边三角形的性质和判定,解题的关键是熟练掌握并应用旋转的性质求解.
2.(1)证明见解析
(2)证明见解析
【分析】(1)直接利用旋转的性质得出,,因为,从而得到,从而证明,即可得到;
(2)根据旋转的性质得到,,从而得到,再利用(1)和勾股定理即可得到答案.
【详解】(1)证:四边形ABCD为正方形,
,
由旋转可得,,
,
,
,
在和中,
,
.
(2)证:由旋转可得,
,,
,
,
,
,
,
.
【点睛】本题主要考查了旋转的性质、全等三角形的判定和性质、勾股定理等知识,由旋转的性质正确得到证明三角形全等的条件是解题的关键.
3.(1)见解析
(2)15
【分析】(1)由旋转性质及等边三角形的判定即可得到证明;
(2)由旋转的性质及等边三角形的性质即可求得结果.
【详解】(1)证明:∵是等边三角形,
∴,,
将绕点旋转得到.
,
是等边三角形 ;
(2)解:∵将绕点旋转得到.
,
的周长
又,
的周长
【点睛】本题考查了等边三角形的判定与性质,旋转的性质,掌握这些知识并灵活运用是关键.
4.(1)见解析
(2)
【分析】(1)由旋转的性质可得,利用证明,根据全等三角形的对应边相等即可得出;
(2)根据等腰三角形的性质以及三角形内角和定理求出,那么.由,得出,再根据三角形外角的性质即可求出.
【详解】(1)解:证明:,
.
将线段绕点旋转到的位置,
.
在与中,
,
,
;
(2),,
,
.
,
,
,
.
【点睛】本题考查了旋转的性质,全等三角形的判定与性质,等腰三角形的性质,三角形内角和定理以及三角形外角的性质,证明是解题的关键.
5.(1)见解析
(2)见解析
【分析】(1)首先根据旋转的性质得到,,然后证明出,即可得到;
(2)根据等边对等角得到,然后利用全等三角形的性质得到,进而证明,最后利用平行线的性质求解即可.
【详解】(1)解:证明:由旋转性质得:,,
,
又,
,
;
(2),
,
若,则,
,
,
,
,
,
.
【点睛】本题考查了旋转的性质、平行线的性质和判定、全等三角形的判定与性质、等腰三角形的性质等,熟练掌握和应用相关的性质与定理是解题的关键.
6.(1)详见解析
(2)
【分析】(1)由旋转的性质就可以证明;
(2)先证出是等边三角形,又根据,得出,再根据勾股定理的逆定理得出,等量代换得出.
【详解】(1)∵绕点C顺时针旋转得到,
∴,,
∵是等边三角形,
∴,,
∴,,...
在和中,
,,,
∴,
∴..
(2)∵,,
∴是等边三角形,
∴,,
∵,
∴,,
∵,
∴,
∴,
∴
∴
【点睛】本题考查了全等三角形的性质与判定,等边三角形的性质,勾股定理的逆定理,旋转的性质,解答时证明三角形全等是关键.
7.(1)
(2)
【分析】(1)由旋转的性质可得,,,,,由等腰三角形的性质可得,可证,通过证明四边形是矩形,可得,由等腰直角三角形的性质可求解;
(2)由垂线段最短可得当时,的长度有最小值,先证点,点,点三点共线,由勾股定理可求的长,由正方形的性质可得,即可求解.
【详解】(1)解:如图,连接,
将绕点顺时针旋转得到,
,,
,,,
,
,
,
、、三点共线;
将线段绕点顺时针旋转得到,
,
,
,
,
,
四边形是平行四边形,
又
四边形是矩形,
,
,,
,
则;
(2)点在边上,
当时,的长度有最小值,
由旋转的性质可得:
,
,
,
,
点,点,点三点共线,
,
,
又,
四边形是正方形,
,
,,,
,
,
线段的最小值为.
【点睛】本题是几何变换综合题,考查了旋转的性质,全等三角形的性质,等腰三角形的性质,矩形的判定和性质,勾股定理等知识,灵活运用这些性质解决问题是解题的关键.
8.(1)见解析
(2),理由见解析
【分析】(1)先证明四边形是平行四边形,再根据得出结论;
(2)先证出,再根据三角形内角和,得到,等量代换即可得到结论.
【详解】(1)证明:∵,
∴,
∵,
∴,,
∵平分,
∴,
∴,
∴,
∴四边形是平行四边形,
又∵,
∴四边形是菱形;
(2)结论:.
证明:∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
【点睛】本题考查了菱形的判定定理、全等三角形的判定和性质、三角形内角和定理等,灵活运用知识,利用数形结合思想,做出辅助线是解题的关键.
9.(1)见解析
(2)
【分析】(1)根据旋转的性质知,,再利用角平分线的判定可得结论;
(2)根据旋转前后三角形全等可得,再说明,则,最后利用面积法求出的长即可.
【详解】(1)解:证明:将绕点逆时针旋转至处,分别延长与交于点,
,,
平分;
(2),
,
,
平分,,
,
,
垂直平分,
,
,
,
在中,由勾股定理得,,
.
【点睛】本题主要考查了旋转的性质,角平分线的判定,等腰三角形的判定与性质,三角形的面积等知识,熟练掌握等腰三角形的判定与性质是解题的关键.
10.(1)四边形是平行四边形,证明见解析
(2)
【分析】(1)依据题意可得到,,,利用平行线的性质可证明,然后依据证明,由全等三角形的性质可知,由旋转的性质可得到,从而可证明,最后依据平行四边形的判定定理进行证明即可;
(2)连接.可证明为等边三角形,则,利用直角三角形的性质可得到答案.
【详解】(1)解:四边形是平行四边形.
证明:四边形是矩形,
,
,
四边形是矩形,
,,
在和中,
,
,
,
矩形由矩形旋转得到,
,,
四边形为平行四边形;
(2)当时,四边形是菱形,
连接.
四边形为菱形,
.
由旋转的性质可知.
.
为等边三角形.
.
.
.
又,
.
故答案为:.
【点睛】本题考查了旋转的性质、全等三角形的判定与性质、等边三角形的判定、平行四边形的判定、矩形的性质、菱形的性质等知识,熟练掌握相关图形的性质和判定定理是解题的关键.
11.(1)a=5,b=1;(2)t=15(s);(3)15,22.5.
【分析】(1)依据|a﹣5|+(b﹣1)2=0,即可得到a,b的值;
(2)依据∠ABO+∠BAO=90°,∠ABQ+∠BAM=180°,即可得到射线AM、射线BQ第一次互相垂直的时间;
(3)分两种情况讨论,依据∠ABQ'=∠BAM“时,BQ'∥AM“,列出方程即可得到射线AM、射线BQ互相平行时的时间.
【详解】解:(1)|a﹣5|+(b﹣1)2=0,
∴a﹣5=0,b﹣1=0,
∴a=5,b=1,
故答案为5,1;
(2)设至少旋转t秒时,射线AM、射线BQ互相垂直.
如图,设旋转后的射线AM、射线BQ交于点O,则BO⊥AO,
∴∠ABO+∠BAO=90°,
∵PQ∥MN,
∴∠ABQ+∠BAM=180°,
∴∠OBQ+∠OAM=90°,
又∵∠OBQ=t°,∠OAM=5t°,
∴t°+5t°=90°,
∴t=15(s);
(3)设射线AM再转动t秒时,射线AM、射线BQ互相平行.
如图,射线AM绕点A顺时针先转动18秒后,AM转动至AM'的位置,∠MAM'=18×5=90°,
分两种情况:
①当9<t<18时,∠QBQ'=t°,∠M'AM“=5t°,
∵∠BAN=45°=∠ABQ,
∴∠ABQ'=45°﹣t°,∠BAM“=5t﹣45°,
当∠ABQ'=∠BAM“时,BQ'∥AM“,
此时,45°﹣t°=5t﹣45°,
解得t=15;
②当18<t<27时,∠QBQ'=t°,∠NAM“=5t°﹣90°,
∵∠BAN=45°=∠ABQ,
∴∠ABQ'=45°﹣t°,∠BAM“=45°﹣(5t°﹣90°)=135°﹣5t°,
当∠ABQ'=∠BAM“时,BQ'∥AM“,
此时,45°﹣t°=135°﹣5t,
解得t=22.5;
【点睛】本题主要考查了平行线的性质,非负数的性质以及角的和差关系的运用,解决问题的关键是运用分类思想进行求解,解题时注意:若两个非负数的和为0,则这两个非负数均等于0.
12.(1)存在,t为3秒,BE的最小值为
(2)或
【分析】(1)根据“垂线段最短”可知:当时,为最小.过点作于点,先证,进而可依据“”判定和全等,从而得,,然后再求出,,进而可得出答案;
(2)先求出,,根据为等腰三角形,有以下三种情况:①当时,则,故此种情况不存在;②当时,则,则,据此得,则,由此即可求出的值;③当时,则,过点作于点,先证为等腰直角三角形,设,则,,,由此得,则,再由得,由此即可求出的值,综上所述即可得出答案.
【详解】(1)解:存在最小值.
根据“垂线段最短”可知:当时,为最小.
,
,
过点作于点,如图:
,
,
,
由旋转的性质得:,,
,
,
,
,,
,
在和中,
,
,
,,
,,
,
在中,,,
,
,
由勾股定理得:,
,,
运动的时间秒,的最小值为;
(2)由(1)可知:,
为的平分线,
,
当点从点出发时,点从点向点与点同时同速运动,
速度每秒1个单位长度,时间为秒,
,
当为等腰三角形时,有以下三种情况:
①当时,则,如图:
,
,这与三角形的任意一个外角都大于和它不相邻的一个内角相矛盾,此种情况不存在;
②当时,则,如图:
,
,
在中,,
,
,
解得:,
③当时,则,过点作于点,如图:
,
,
为等腰直角三角形,
设,
在中,,,则,
由勾股定理得:,
,
,
,
,
即:,
解得:.
综上所述:当为等腰三角形时,的值为或.
【点睛】此题主要考查了图形的旋转变换及性质,全等三角形的判定和性质,等腰三角形的性质,垂线段的性质,含有角的直角三角形的性质,熟练掌握全等三角形的判定和性质,理解垂线段最短时解答此题的关键,难点是分类讨论思想与方程思想在解题中的应用,漏解是解答此题的易错点.
13.(1)
(2)同意,图见解析,或
【分析】(1)由可得,再由,得到,最后求出的度数即可;
(2)由 可得,再求出度数.
【详解】(1)如图1当
所以
因为,
所以
因为
所以
(2)同意
如图2
当
所以
所以
综上或
【点睛】本题考查了平行线的性质,解决本题的关键是熟练掌握平行线的性质.
14.(1)150°;(2)EF2=BE2+FC2.(3).
【分析】(1)由△ACP′≌△ABP可得旋转角∠PAP′=60°,可得△APP′为等边三角形,根据勾股定理逆定理可证明△PP′C为直角三角形,根据∠APB=∠AP′C=∠AP′P+∠PP′C即可得答案;(2)如图2,把△ABE绕点A逆时针旋转90°得到△ACE′,由旋转的性质可得AE′=AE,CE′=BE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,根据角的和差关系可得∠EAF=∠E′AF,利用SAS可证明△EAF≌△E′AF,可得E′F=EF,根据等腰直角三角形的性质可得∠E′CF=90°,根据勾股定理即可得结论;(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,根据含30°角的直角三角形的性质及勾股定理可求出AB、BC的长,根据旋转的性质可得∠A′BC=90°,△BOO′是等边三角形,由∠AOC=∠COB=∠BOA=120°,利用平角的定义可证明C、O、A′、O′四点共线,利用勾股定理求出A′C的长即可得答案.
【详解】(1)∵△ACP′≌△ABP,
∴AP′=AP=3、CP′=BP=4、∠AP′C=∠APB,
由题意知旋转角∠PAP′=60°,
∴△APP′为等边三角形,
∴P′P=AP=3,∠AP′P=60°,
∵P′C=PB=4,PC=5,
∴PC2=P′C2+P′P2,
∴△PP′C为直角三角形,且∠PP′C=90°,
∴∠APB=∠AP′C=∠AP′P+∠PP′C=60°+90°=150°.
故答案为150°
(2)如图2,把△ABE绕点A逆时针旋转90°得到△ACE′,
由旋转的性质得,AE′=AE,CE′=BE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,
∵∠EAF=45°,
∴∠E′AF=∠EAE′-∠EAF=45°,
∴∠EAF=∠E′AF,
在△EAF和△E′AF中,
∴△EAF≌△E′AF(SAS),
∴E′F=EF,
∵∠CAB=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠E′CF=45°+45°=90°,
由勾股定理得,E′F2=CE′2+FC2,
即EF2=BE2+FC2.
(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,
∵在Rt△ABC中,∠ACB=90°,AC=1,∠ABC=30°,
∴AB=2,
∴BC=,
∵△AOB绕点B顺时针方向旋转60°,∠ABC=30°,
∴∠A′BC=∠ABC+60°=30°+60°=90°,
∵∠C=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO,
∴△BOO′是等边三角形,
∴BO=OO′,∠BOO′=∠BO′O=60°,
∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°,
∴C、O、A′、O′四点共线,
在Rt△A′BC中,A′C=,
∴OA+OB+OC=A′O′+OO′+OC=A′C=.
【点睛】本题考查了旋转的性质、等边三角形的判定与性质、等腰直角三角形的性质及含30°角的直角三角形的性质,熟练掌握旋转的性质,正确得出对应边和对应角是解题关键.
15.(1)3,1
(2)
(3)
【分析】(1)根据二元一次方程的解,,为正整数,即可求解;
(2)设运动时间为,依题意,,则,,过点作,则,根据平行线的性质得出,根据已知条件得出,建立方程求得,进而得出,根据,进而即可求解;
(3)先转动30秒,射线才开始转动,当到达之前,当从返回且到达前,根据平行线的性质,列出方程,解方程即可求解.
【详解】(1)解:,,为正整数,
,
,;
(2)设运动时间为,
由题意得,,则,,
过点作,则,
,
,
,
,
,
,
,
,
,
,
解得:,
,
;
(3)依题意,线先转动30秒,射线才开始转动,
当到达之前,当时,则,
,
解得:;
当从返回且到达前,当时,则,
,
解得:.
【点睛】本题考查了二元一次方程的解,平行线的性质与判定,一元一次方程的应用,熟练掌握平行线的性质是解题的关键.
16.(1)
(2)①当旋转时间为3或21秒时,成立;②旋转的时间是25秒
【分析】(1)根据平角即可得到结论;
(2)①如解图1,根据平行线的性质得到,求得,于是得到结论;如解图2,根据平行线的性质得到,根据三角形的内角和得到,求得,于是得到结论;②设旋转的时间为t秒,由题知,,根据周角得到,列方程即可得到结论.
【详解】(1)∵,
∴,
故答案为:;
(2)①如解图1,此时,成立,
∵,
∴,
∵,
∴,
∴,
∵转速为秒,
∴旋转时间为3秒;
如解图2,,
∵,
∴,
∵,
∴,
∴,
∵三角板绕点P逆时针旋转D的角度为,
∵转速为秒,
∴旋转时间为21秒,
综上所述,当旋转时间为3或21秒时,成立;
②设旋转的时间为t秒,由题知,,
∴,
∴,
当,即,
解得:,
∴当,旋转的时间是25秒.
【点睛】本题考查了旋转的性质,平行线的性质,三角形的内角和,识别图形是解题的关键.
17.(1);
(2).
【分析】(1)利用证明,推出,即可得到;
(2)利用旋转的性质以及矩形的判定定理得到四边形是矩形,根据矩形的性质即可求解.
【详解】(1)证明:∵正方形,
∴,.
∵,
∴.
∴.
∴.
又∵,
∴.
在△AED和△BFA中,
∵,,.
∴.
∴.
∵,
∴.
(2)解:如图,
由题设得,
∴,
由旋转的性质知:,,
∴,
∴.
∴四边形为平行四边形.
又∵,
∴四边形是矩形.
∴.
【点睛】此题考查了正方形的性质,全等三角形的判定与性质,矩形的判定与性质,以及旋转的性质,熟练掌握判定与性质是解本题的关键.
18.(1)
(2)
(3)或
【分析】(1)根据平行线的性质得出,得出,即可求解.
(2)设交于点,则,过点作,推出.根据平行线的性质得出则.求出,即可求解;
(3)根据题意,进行分类讨论:①当点在上方时,②当点在下方时,正确画出图形,根据平行线的性质求解即可.
【详解】解:(1)∵,
.
又,
,
.
(2)如图1,设交于点,则,过点作,
∵,
.
.
.
又,
,
.
(3)或.
如图2,交于点,当点在上方时,
设,则,
∴,
解得.
∴;
如图3,延长交于点,当点在下方时,
设,则,
∴,
解得,
∴.
综上所述,的度数为或.
【点睛】本题主要考查了平行线的性质,解题的关键是掌握平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.
19.(1)105°
(2)150°
(3)75°或255°
【分析】(1)根据三角形的内角和即可求解;
(2)根据角平分线的定义可得,从而得出,最后根据平行线的性质即可求解;
(3)根据题意,画出图形,进行分类讨论:①在上方时,设与相交于F,②当在的下方时,设直线与相交于F.
【详解】(1)解:∵,,
∴在中,.
故答案为:.
(2)∵平分,
∴,
∴,
∴,
∴;
(3)如图1,在上方时,设与相交于F,
∵,
∴,
在中,,
,
,
当在的下方时,设直线与相交于F,
∵,
∴,
在中,,
∴旋转角为,
综上所述,当边旋转或时,边恰好与边平行.
【点睛】本题考查了旋转的性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,直角三角形两锐角互余的性质,熟记各性质并熟悉三角板的度数特点是解题的关键.
20.知识探究:,理由见解析;拓展探究:EM=EN,理由见解析;迁移运用:见解析
【分析】知识探究:根据正方形的性质可得,平分,再根据垂直定义可得,从而可得四边形是矩形,然后利用矩形的性质可得,从而利用角平分线的性质即可解答.
拓展探究:过点E作,垂足为P,过点E作,垂足为Q,根据垂直定义可得,再根据正方形的性质可得,平分,从而可得四边形是矩形,进而可得,然后利用等式的性质可得,再利用角平分线的性质可得,从而证明,最后利用全等三角形的性质即可解答;
迁移运用:连接,根据正方形的性质可得,平分,从而可得,然后证明,从而可得,进而可得,最后利用等腰三角形的三线合一性质即可解答.
【详解】解:知识探究:,
理由:∵四边形是正方形,
∴,平分,
∵,
∴,
∵,
∴四边形是矩形,
∴,
∴;
拓展探究:,
理由:过点E作,垂足为P,过点E作,垂足为Q,
∴,
∵四边形是正方形,
∴,平分,
∴四边形是矩形,
∴,
∵,
∴,
∴,
∵平分,,,
∴,
∴,
∴;
迁移运用:连接,
∵四边形是正方形,
∴,平分,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴H是线段的中点.
【点睛】本题考查了旋转的性质,正方形的性质,全等三角形的判定与性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
21.(1)证明见解析
(2)不同意,理由见解析
(3)
【分析】(1)由四边形与均为正方形,得,,,,进而有,于是即可证明结论成立;
(2)证明四边形的面积总等于正方形面积的即可;
(3)由(2)即可得解.
【详解】(1)证明:四边形与均为正方形,
,,,,
,
,
即,
.
(2)解:不同意,理由:
由(1)可知:,
,
,
即当正方形绕点O转动时,四边形的面积总等于正方形面积的.
(3)解:∵,正方形的边长为a,
∴,
故答案为.
【点睛】本题主要考查了正方形的性质,全等三角形的判定和性质,得到是解题的关键.
22.(1)130°;(2)∠AOD与∠COE的差不发生变化,为30°;(3)∠AOE=131.25°或175°.
【分析】(1)求出∠COE的度数,即可求出答案;
(2)分为两种情况,根据∠AOC=90°和∠DOE=60°求出即可;
(3)根据∠AOE=7∠COD、∠DOE=60°、∠AOC=90°求出即可.
【详解】(1)∵OC⊥AB,
∴∠AOC=90°,
∵OD在OA和OC之间,∠COD=20°,∠EOD=60°,
∴∠COE=60°-20°=40°,
∴∠AOE=90°+40°=130°,
故答案为130°;
(2)在△ODE旋转过程中,∠AOD与∠COE的差不发生变化,
有两种情况:①如图1、∵∠AOD+∠COD=90°,∠COD+∠COE=60°,
∴∠AOD-∠COE=90°-60°=30°,
②如图2、∵∠AOD=∠AOC+∠COD=90°+∠COD,∠COE=∠DOE+∠DOC=60°+∠DOC,
∴∠AOD-∠COE=(90°+∠COD)-(60°+∠COD)=30°,
即△ODE在旋转过程中,∠AOD与∠COE的差不发生变化,为30°;
(3)如图1、∵∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,
∴90°+60°-∠COD=7∠COD,
解得:∠COD=18.75°,
∴∠AOE=7×18.75°=131.25°;
如图2、∵∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,
∴90°+60°+∠COD=7∠COD,
∴∠COD=25°,
∴∠AOE=7×25°=175°,
即∠AOE=131.25°或175°.
【点睛】本题考查了角的有关计算的应用,能根据题意求出各个角的度数是解此题的关键.注意分类思想的运用.
23.(1),理由见解析
(2)见解析
(3)见解析
【分析】(1)先根据旋转的性质得,,则可判断为等边三角形,所以,,再利用为等边三角形得到,,则可得到;
(2)通过证明得到;
(3)先判断为等边三角形得到,,再与(2)的证明方法一样证明得到,所以,加上,从而可判断四边形是平行四边形.
【详解】(1)解:.
理由如下:逆时针旋转得到,
,,
为等边三角形,
,,
为等边三角形,
,,
,,
;
(2)证明:在和中,
,
,
;
(3)证明:顺时针旋转得到,
,,
为等边三角形,
,,
为等边三角形,
,,
,,
;
在和中,
,
,
,
,
,
四边形是平行四边形.
【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质、全等三角形的判定与性质和平行四边形的判定.
24.探究:成立,证明见解析;应用:①45;②.
【分析】探究:根据旋转的性质得出,然后利用证明即可;
应用:①根据全等三角形的性质可得答案;
②利用勾股定理求出,可得的长,根据全等三角形的性质可得的长,求出,根据勾股定理可得答案.
【详解】探究:成立,
证明:∵和都是等腰直角三角形,
∴,,
∵将绕点A逆时针旋转,
∴,
在与中,,
∴,
∴;
应用:①∵是等腰直角三角形,
∴,
同探究可得:,
∴,
故答案为:45;
②∵在中,,
∴,
∴,
∵
∴,
∵,,
∴,
∴,
∴.
【点睛】本题是几何变换综合题,主要考查了等腰直角三角形的性质,旋转的性质,全等三角形的判定与性质,勾股定理,证明是解题的关键.
25.(1)
(2)
(3)或或或
【分析】(1)先计算的度数,再根据角平分线的定义和旋转的速度可得的值;
(2)分别表示与的度数,相减可得数量关系;
(3)分四种情况讨论:分别和三边平行,还有,计算旋转角并根据速度列方程可得结论.
【详解】(1)解:如图2,,,
,
平分,
,
,
答:此时的值是;
(2)当旋转至的内部时,如图3,与的数量关系是:;
理由是:由旋转得:,
,,
;
(3)分四种情况:
①当时,如图4,,
;
②当时,如图5,则,
,
;
③当时,如图6,则,
,
;
④当时,如图7,
,
,
;
综上,的值是或或或.
故答案为:或或或.
【点睛】本题考查了平行线的性质,角平分线的定义,是典型的实际操作问题,将两个三角板按照题意进行摆放,旋转,清楚每一时刻各个角的度数是多少和各角之间的关系.
26.(1)3;21
(2)当t为6或15或24时,有两个内角相等
(3)105
【分析】(1)由平行和垂直求出旋转角,结合旋转速度求出旋转时间;
(2)画出图形,分类讨论,①;②;③,求出旋转角,再求出值;
(3)找出与,,,有关的数量关系,再把无关的角消去,得出结论.
【详解】(1)解:如图(1),当时,
平分,,
,
又为的一个外角,
,
;
如图(2),当时,
,
,
,
,
.
故答案为:3;21.
(2)①如图(3),当时,
,
,
;
②如图(4),当时,
,,
,
;
③如图(5),当时,
,
,
综上所述:当为6或15或24时,有两个内角相等.
(3)是为定值105,理由如下:
是的一个外角,是的一个外角,
,,
又,,
,
,
.
【点睛】本题以求三角形旋转时间为背景,考查了学生对图形的旋转变换、平行的性质、垂直的性质和求等腰三角形内角的掌握情况,第(2)问分情况讨论是解决问题的关键,第(3)问找到三个角之间的关系是关键.
27.(1),理由见解析
(2)A、;B、
【分析】(1)由“”可证,可得;
(2)、由等腰三角形的性质可求,由全等三角形的性质可求,即可求解;、分两种情况讨论,由等腰三角形的性质和全等三角形的性质可求解.
【详解】(1)解:,理由如下:
,,
,
将线段绕点按逆时针方向旋转得到线段,
,,
,
在和中,
,
,
;
(2)、如图:
,,
,
,
,
,
;
、如图,当点在线段上时,
,,
,
,
,
,
;
如图,当点在线段上时,
,,
,
,
,
,
;
如图,当点在线段上时,
同理可求,
综上所述:或.
【点睛】本题考查了旋转的性质,等腰三角形的性质,全等三角形的判定和性质,利用分类讨论思想解决问题是解题的关键.
28.(1)∠EFB=15°;(2)①30°;②存在,图见解析,∠ECB=120°、165°、150°、60°或15°.
【分析】(1)根据直角三角形内角和的性质即可得到答案;
(2)①根据平行线的性质即可得到答案;
②分5种情况讨论,根据平行线的性质进行计算,即可得到答案.
【详解】解:(1)∵∠A=30°,∠CDE=45°,
∴∠ABC=90°﹣30°=60°,∠E=90°﹣45°=45°,
∴∠EFB=∠ABC﹣∠E=60°﹣45°=15°;
(2)①∵CD∥AB,
∴∠ACD=∠A=30°,
∵∠ACD+∠ACE=∠DCE=90°,
∠ECB+∠ACE=∠ACB=90°,
∴∠ECB=∠ACD=30°;
②如图1,CE∥AB,∠ACE=∠A=30°,
∠ECB=∠ACB+∠ACE=90°+30°=120°;
如图2,DE∥AB时,延长CD交AB于F,
则∠BFC=∠D=45°,
在△BCF中,∠BCF=180°﹣∠B﹣∠BFC,
=180°﹣60°﹣45°=75°,
∴∠ECB=∠BCF+∠ECF=75°+90°=165°;
如图3,CD∥AB时,∠BCD=∠B=60°,
∠ECB=∠BCD+∠EDC=60°+90°=150°;
如图4,CE∥AB时,∠ECB=∠B=60°,
如图5,DE∥AB时,∠ECB=60°﹣45°=15°.
【点睛】本题考查三角形内角和的性质、平行线的性质,解题的关键是掌握三角形内角和的性质、平行线的性质,分5种情况讨论解答.
29.(1)4(2)
【分析】(1)根据正方形的性质得出,,,推出,证出,即可得出结果;
(2)发生变化,对旋转角分情况讨论即可.
【详解】解:(1)连接,,
四边形和四边形都是正方形,
,,,
,
在与中,
,
,
四边形的面积等于三角形的面积,
即重叠部分面积不变,总是等于正方形面积的,
;
(2)设等边绕着点的旋转角为,等边的边长等于4,则高为,
①如图,当经过点时,若此时开始旋转,,重叠部分的形状为直角三角形,
,
②如图,当旋转至图中位置时,,重叠部分的形状为菱形,
,
③如图,当旋转至图中位置时,,重叠部分的形状为等边三角形,
,
④如图,当旋转至图中位置时,,重叠部分的形状为直角三角形,
,
综上所述,这两个等边三角形重叠部分的面积是变化的,的变化范围是.
【点睛】本题考查正方形的性质和等边三角形的性质,找出面积之间的关系是解题关键.
30.问题发现:①③④
数学思考:,,理由见解析
拓展应用:
【分析】●问题发现:由等腰三角形的性质判断①,作辅助线构造三角形判断②,由过一点有且只有一条直线垂直于已知直线判断③,由③的结论可以判断④;
●数学思考:连接,,由是等边三角形可得,,,,然后证明,进而证明结论;
●拓展应用:分两种情况利用勾股定理解题即可.
【详解】解:●问题发现:
∵是边的中点,是等边三角形,
∴,
又∵,
∴,所以①正确;
过D作交于点G,
∴
∵和都是等边三角形,
∴,
∴,
∴四边形为平行四边形,
∴,所以②不正确;
连接,
∵和都是等边三角形,
∴,
∵
∴,
∴三点共线,即,所以③正确;
由③可知整个图形关于直线成轴对称图形,所以④正确;
故答案为:①③④.
●数学思考:,.理由如下:
连接,,由图1,,,
可得.绕着点旋转,
仍然成立.∵是等边三角形,
∴,.
∴.
同理,,.
∴,.
∴.
∴.
∴,.
延长交于点,交于点,
又,∴.
∴.
∴.
●拓展应用
当时,∵,∴,,三点共线.
如备用图1,
设,则.∵,
∴在中,.
解之得:.又,
∴
即.
如备用图2.
设,则.∵,
∴在中,.
解之得:.
又,∴
即.
综上所述,.
【点睛】本题考查等边三角形的性质,勾股定理,旋转的性质,相似三角形的判定和性质,掌握等边三角形的性质和旋转的性质是解题的关键.
答案第1页,共2页
答案第1页,共2页
(2023春 秦都区期末)
1.如图,是等边三角形,点 E在边上,连接,将绕点 B逆时针旋转60°得到,连接 .
(1)求证:;
(2)若,求的周长.
(2023春 北林区期末)
2.如图,在正方形ABCD中,E,F是对角线BD上两点,且,将绕点A顺时针旋转后,得到,连接.
(1)求证:;
(2)求证:.
(2022秋 同心县期末)
3.如图,是等边三角形,点在边上,将绕点旋转得到.
(1)求证:是等边三角形
(2)若,求的周长.
(2023春 清远期末)
4.如图,在中,点在边上,,将线段绕点旋转到的位置,使得,连接,与交于点.
(1)求证:;
(2)若,,求的度数.
(2023春 白银期中)
5.如图,在四边形中,,,,点在对角线上,将线段绕点顺时针旋转,得到线段,连接.
(1)求证:;
(2)若,求证:.
(2023春 南城县期中)
6.如图,点O是等边三角形内一点,将绕点C顺时针旋转得到,连接.
(1)求证:;
(2)若,,,求的度数.
(2023春 罗源县校级期中)
7.如图,先将绕点顺时针旋转得到,再将线段绕点顺时针旋转得到,连接、、,且.
(1)若.、、三点在同一条直线上,求的长;
(2)若,,点在边上,求线段的最小值.
(2023春 成武县期中)
8.已知,,.
(1)如图1,平分,求证:四边形是菱形;
(2)如图2,将(1)中的绕点逆时针旋转(旋转角小于),,的延长线相交于点,用等式表示与之间的数量关系,并证明.
(2023春 九江期末)
9.如图,在中,,将绕点逆时针旋转至处,分别延长与交于点,连接、.
(1)求证:平分;
(2)若,,求的长.
(2023春 盱眙县期末)
10.如图,将矩形绕点旋转得到矩形,点在上,延长交于点.连接、.
(1)四边形是怎样的特殊四边形?证明你的结论;
(2)若长为2,则的长为 时,四边形为菱形.
(2023春 平山县期末)
11.如图,PQ∥MN,A、B分别为直线MN、PQ上两点,且∠BAN=45°,若射线AM绕点A顺时针旋转至AN后立即回转,射线BQ绕点B逆时针旋转至BP后立即回转,两射线分别绕点A、点B不停地旋转,若射线AM转动的速度是a°/秒,射线BQ转动的速度是b°/秒,且a、b满足|a﹣5|+(b﹣1)2=0.(友情提醒:钟表指针走动的方向为顺时针方向)
(1)a= ,b= ;
(2)若射线AM、射线BQ同时旋转,问至少旋转多少秒时,射线AM、射线BQ互相垂直.
(3)若射线AM绕点A顺时针先转动18秒,射线BQ才开始绕点B逆时针旋转,在射线BQ到达BA之前,问射线AM再转动多少秒时,射线AM、射线BQ互相平行?
(2023春 振兴区校级期中)
12.如图(1),在中,,,射线于点,动点从点出发沿射线方向运动;以每秒1个单位长度的速度运动,运动时间为秒;
(1)以点为旋转中心,将逆时针旋转,得到线段,连接,是否存在最小值,不存在,则说明理由,存在则求出最小时的值及的最小值;
(2)若射线为的平分线,当点从点出发时,点从点向点与点同时同速运动,连接交于点,当为等腰三角形时,直接写出所有可能的t值.
(2023春 迁安市期中)
13.老师在黑板上出示题目:
如图,在中,,线段与CB边重合,从现在的位置绕着点C按逆时针方向旋转一周回到原来的位置是否有一位置使 如果有这样的位置,请画出示意图,并求出的度数,如果没有说明理由?
(1)嘉嘉认为:有这样一个位置,使得,如图.请你按照嘉嘉的做法,求出的度数.
(2)琪琪认为:嘉嘉的想法不全面,还存在另外一种情况使得你是否同意琪琪的说法?如果同意,请画出图形,并求出此时的度数;如果不同意,请说明理由.
(2022秋 青山湖区期末)
14.阅读下面材料,并解决问题:
(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=__________;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
(2023春 清江浦区期末)
15.如图1,,点在直线上,点在直线上,射线绕点顺时针从射线旋转至射线后便立即回转;射线绕点顺时针从射线旋转至射线后便立即回转:射线、射线不停地来回旋转.若射线转动的速度是度秒,射线转动的速度是度秒,且、是方程的正整数解.
(1) , ;
(2)如图2,若,两条射线同时转动,在射线到达之前,若两条射线交于点,过作交于,若,求的度数;
(3)若射线先转动30秒,射线才开始转动,在射线到达之前,射线转动几秒,射线与射线互相平行?
(2023春 蒸湘区期末)
16.如图,有一副直角三角板如图1放置(其中),与直线重合,且三角板,三角板均可以绕点P逆时针旋转.
(1)在图1中, ;
(2)①如图2,若三角板保持不动,三角板绕点P逆时针旋转,转速为秒,转动一周三角板就停止转动,在旋转的过程中,当旋转时间为多少时,有成立;
②如图3,在图1基础上,若三角板的边从处开始绕点P逆时针旋转,转速为秒,同时三角板的边从处开始绕点P逆时针旋转,转速为秒,当转到与重合时,两三角板都停止转动,在旋转过程中,当时,求旋转的时间是多少?
(2023春 雄县期中)
17.教材中有这样一道题:如图1,四边形是正方形,是上的任意一点,于点,,且交于点.求证:.
小明通过证明解决了问题,在此基础上他进一步提出了以下以下回题,请你解答.
(1)若图1中的点为延长线上一点,其余条件不变,如图2所示,猜想此时,,之间的数量关系,并证明你的结论.
(2)将图1中的绕点逆时针旋转,使得与重合,记此时点的对应点为点,如图3所示,若正方形的边长为3,求的长度.
(2023春 长垣市期末)
18.综合与实践
数学社团的同学以“两条平行线,和一块含角的直角三角尺”为主题开展数学活动,已知点E,F不可能同时落在直线和之间.
探究:(1)如图1,把三角尺的角的顶点E,G分别放在,上,若,求的度数;
类比:(2)如图2,把三角尺的锐角顶点G放在上,且保持不动,若点E恰好落在和之间,且与所夹锐角为,求的度数;
迁移:(3)把三角尺的锐角顶点G放在上,且保持不动,旋转三角尺,若存在,直接写出射线与所夹锐角的度数.
(2023春 阳城县期末)
19.如图1,将一副直角三角板放在同一条直线上,其中,.
(1)观察猜想:将图1中的三角尺沿的方向平移至图2的位置,使得点O与点N重合,与相交于点E,则 ;
(2)操作探究:将图1中的三角尺绕点O按顺时针方向旋转,使一边在的内部,如图3,且OD恰好平分,与相交于点E,求的度数;
(3)深化拓展:将图1中的三角尺绕点O按沿顺时针方向旋转一周,在旋转的过程中,当边旋转多少度时,边恰好与边平行?
(2023春 岱岳区期末)
20.知识探究:如图1,点E是正方形对角线AC上任意一点,以点E为直角顶点的直角两边,分别角与,相交于M点,N点.当时,请探究与的数量关系,并说明理由;
拓展探究:当绕点E顺时针旋转到点M与点D重合时,如图2,请探究与的数量关系,并说明理由;
迁移运用:在图2的基础上,过点E作于点H,如图3,证明H是线段的中点.
(2023春 顺平县期末)
21.如图,正方形的对角线相交于点O,点O又是正方形的一个顶点,且这两个正方形边长相等.与相交于点M,与相交于点N.
(1)求证:;
(2)嘉琪说:当正方形绕点O转动,且与垂直时,四边形的面积最小.你同意嘉琪的说法吗?请说明理由;
(3)若正方形的边长为a,用含a的代数式表示两个正方形重叠部分的面积为______.
(2023春 沈丘县期末)
22.如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE=______;
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
(2023春 东昌府区期末)
23.在等边三角形的内部有一点,连接,,以点为中心,把逆时针旋转得到,连接,.以点为中心,把顺时针旋转得到,连接,.
(1)判断和的大小关系,并说明理由;
(2)求证:;
(3)求证:四边形是平行四边形.
(2022秋 河口区期末)
24.感知:如图①,和都是等腰直角三角形,,点在线段上,点在线段上,我们很容易得到,不需证明.
探究:如图②,将绕点逆时针旋转,连结和,此时是否依然成立?若成立,写出证明过程;若不成立,说明理由.
应用:如图③,当绕点逆时针旋转,使得点落在的延长线上,连结.
①的度数为______度;
②若,,则线段的长为______.
(2023春 内乡县期末)
25.将一副直角三角板如图1,摆放在直线MN上(直角三角板和直角三角板,,,,),保持三角板不动,将三角板绕点以每秒的速度顺时针旋转,旋转时间为秒,当与射线重合时停止旋转.
(1)如图2,当为的角平分线时,求此时t的值;
(2)当旋转至的内部时,求与的数量关系;
(3)在旋转过程中,当三角板的其中一边平行于三角板的某一边时,求此时t等于 (直接写出答案即可).
(2023春 衡山县期末)
26.一副三角板如图1摆放,,,,点在上,点在上,且平分,现将三角板绕点以每秒的速度顺时针旋转(当点落在射线上时停止旋转),设旋转时间为秒.
(1)当 秒时,;当 秒时,;
(2)在旋转过程中,与的交点记为,如图2,若有两个内角相等,求t的值;
(3)当边与边、分别交于点、时,如图3,连接,设,,,试问是否为定值?若是,请求出定值;若不是,请说明理由.
(2023春 太原期中)
27.如图,已知中,,,点是平面内一点,将线段绕点按逆时针方向旋转得到线段.
(1)当点D在内部时,连接,.请判断线段与的数量关系,并说明理由;
(2)请从A,B两题中任选一题作答.
A.当点D在内部时,若直线恰好经过点B,直接写出的度数.
B.当点D在外部时,若直线恰好经过点C,直接写出的度数.
(2023春 遂平县期末)
28.如图1,将一副三角板的直角重合放置,其中∠A=30°,∠CDE=45°.
(1)如图1,求∠EFB的度数;
(2)若三角板ACB的位置保持不动,将三角板CDE绕其直角顶点C顺时针方向旋转.
①当旋转至如图2所示位置时,恰好CD∥AB,则∠ECB的度数为 ;
②若将三角板CDE继续绕点C旋转,直至回到图1位置.在这一过程中,是否还会存在△CDE其中一边与AB平行?如果存在,请你画出示意图,并直接写出相应的∠ECB的大小;如果不存在,请说明理由.
(2023 碑林区校级模拟)
29.似曾相识
(1)如图①,正方形的边长等于4,中心为,正方形的边长也等于4,在正方形绕着点O旋转的过程中,若将这两个正方形重叠部分的面积记为S,那么S是否为定值?若S为定值,请直接写出该定值;若S变化,请直接写出它的变化范围.
类比探索
(2)如图②,等边的边长等于4,中心为,等边的边长也等于4,在等边绕着点O旋转的过程中,若将这两个等边三角形重叠部分的面积记为S,那么S是否为定值?若S为定值,请直接写出该定值;若S变化,请求出它的变化范围.
(2023 青山湖区模拟)
30.●问题发现
如图1,和都是等边三角形,边和在同一直线上,是边的中点,,连接,则下列结论正确的是__________.(填序号即可)
①;②;③;④整个图形是轴对称图形.
●数学思考
将图1中的绕着点旋转,不动,连接和,如图2,则和具有怎样的数量和位置关系?请给出证明过程;
●拓展应用
已知,,在图1中的绕着点旋转的过程中,当时,求线段的长度.
试卷第2页,共3页
试卷第1页,共3页
参考答案:
1.(1)详见解析
(2)
【分析】(1)利用等边三角形的性质和判定和旋转的性质,证明,即可得解;
(2)由,结合(1)的结论,等线段转化,得到的周长.
【详解】(1)证明:∵是等边三角形,
∴.
∵是由 绕点 B逆时针旋转 60°得到,
∴,
∴是等边三角形,
∴
∴,
∴;
(2)∵和都是等边三角形,
∴
∴的周长为.
【点睛】本题考查了旋转的性质及等边三角形的性质和判定,解题的关键是熟练掌握并应用旋转的性质求解.
2.(1)证明见解析
(2)证明见解析
【分析】(1)直接利用旋转的性质得出,,因为,从而得到,从而证明,即可得到;
(2)根据旋转的性质得到,,从而得到,再利用(1)和勾股定理即可得到答案.
【详解】(1)证:四边形ABCD为正方形,
,
由旋转可得,,
,
,
,
在和中,
,
.
(2)证:由旋转可得,
,,
,
,
,
,
,
.
【点睛】本题主要考查了旋转的性质、全等三角形的判定和性质、勾股定理等知识,由旋转的性质正确得到证明三角形全等的条件是解题的关键.
3.(1)见解析
(2)15
【分析】(1)由旋转性质及等边三角形的判定即可得到证明;
(2)由旋转的性质及等边三角形的性质即可求得结果.
【详解】(1)证明:∵是等边三角形,
∴,,
将绕点旋转得到.
,
是等边三角形 ;
(2)解:∵将绕点旋转得到.
,
的周长
又,
的周长
【点睛】本题考查了等边三角形的判定与性质,旋转的性质,掌握这些知识并灵活运用是关键.
4.(1)见解析
(2)
【分析】(1)由旋转的性质可得,利用证明,根据全等三角形的对应边相等即可得出;
(2)根据等腰三角形的性质以及三角形内角和定理求出,那么.由,得出,再根据三角形外角的性质即可求出.
【详解】(1)解:证明:,
.
将线段绕点旋转到的位置,
.
在与中,
,
,
;
(2),,
,
.
,
,
,
.
【点睛】本题考查了旋转的性质,全等三角形的判定与性质,等腰三角形的性质,三角形内角和定理以及三角形外角的性质,证明是解题的关键.
5.(1)见解析
(2)见解析
【分析】(1)首先根据旋转的性质得到,,然后证明出,即可得到;
(2)根据等边对等角得到,然后利用全等三角形的性质得到,进而证明,最后利用平行线的性质求解即可.
【详解】(1)解:证明:由旋转性质得:,,
,
又,
,
;
(2),
,
若,则,
,
,
,
,
,
.
【点睛】本题考查了旋转的性质、平行线的性质和判定、全等三角形的判定与性质、等腰三角形的性质等,熟练掌握和应用相关的性质与定理是解题的关键.
6.(1)详见解析
(2)
【分析】(1)由旋转的性质就可以证明;
(2)先证出是等边三角形,又根据,得出,再根据勾股定理的逆定理得出,等量代换得出.
【详解】(1)∵绕点C顺时针旋转得到,
∴,,
∵是等边三角形,
∴,,
∴,,...
在和中,
,,,
∴,
∴..
(2)∵,,
∴是等边三角形,
∴,,
∵,
∴,,
∵,
∴,
∴,
∴
∴
【点睛】本题考查了全等三角形的性质与判定,等边三角形的性质,勾股定理的逆定理,旋转的性质,解答时证明三角形全等是关键.
7.(1)
(2)
【分析】(1)由旋转的性质可得,,,,,由等腰三角形的性质可得,可证,通过证明四边形是矩形,可得,由等腰直角三角形的性质可求解;
(2)由垂线段最短可得当时,的长度有最小值,先证点,点,点三点共线,由勾股定理可求的长,由正方形的性质可得,即可求解.
【详解】(1)解:如图,连接,
将绕点顺时针旋转得到,
,,
,,,
,
,
,
、、三点共线;
将线段绕点顺时针旋转得到,
,
,
,
,
,
四边形是平行四边形,
又
四边形是矩形,
,
,,
,
则;
(2)点在边上,
当时,的长度有最小值,
由旋转的性质可得:
,
,
,
,
点,点,点三点共线,
,
,
又,
四边形是正方形,
,
,,,
,
,
线段的最小值为.
【点睛】本题是几何变换综合题,考查了旋转的性质,全等三角形的性质,等腰三角形的性质,矩形的判定和性质,勾股定理等知识,灵活运用这些性质解决问题是解题的关键.
8.(1)见解析
(2),理由见解析
【分析】(1)先证明四边形是平行四边形,再根据得出结论;
(2)先证出,再根据三角形内角和,得到,等量代换即可得到结论.
【详解】(1)证明:∵,
∴,
∵,
∴,,
∵平分,
∴,
∴,
∴,
∴四边形是平行四边形,
又∵,
∴四边形是菱形;
(2)结论:.
证明:∵,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
【点睛】本题考查了菱形的判定定理、全等三角形的判定和性质、三角形内角和定理等,灵活运用知识,利用数形结合思想,做出辅助线是解题的关键.
9.(1)见解析
(2)
【分析】(1)根据旋转的性质知,,再利用角平分线的判定可得结论;
(2)根据旋转前后三角形全等可得,再说明,则,最后利用面积法求出的长即可.
【详解】(1)解:证明:将绕点逆时针旋转至处,分别延长与交于点,
,,
平分;
(2),
,
,
平分,,
,
,
垂直平分,
,
,
,
在中,由勾股定理得,,
.
【点睛】本题主要考查了旋转的性质,角平分线的判定,等腰三角形的判定与性质,三角形的面积等知识,熟练掌握等腰三角形的判定与性质是解题的关键.
10.(1)四边形是平行四边形,证明见解析
(2)
【分析】(1)依据题意可得到,,,利用平行线的性质可证明,然后依据证明,由全等三角形的性质可知,由旋转的性质可得到,从而可证明,最后依据平行四边形的判定定理进行证明即可;
(2)连接.可证明为等边三角形,则,利用直角三角形的性质可得到答案.
【详解】(1)解:四边形是平行四边形.
证明:四边形是矩形,
,
,
四边形是矩形,
,,
在和中,
,
,
,
矩形由矩形旋转得到,
,,
四边形为平行四边形;
(2)当时,四边形是菱形,
连接.
四边形为菱形,
.
由旋转的性质可知.
.
为等边三角形.
.
.
.
又,
.
故答案为:.
【点睛】本题考查了旋转的性质、全等三角形的判定与性质、等边三角形的判定、平行四边形的判定、矩形的性质、菱形的性质等知识,熟练掌握相关图形的性质和判定定理是解题的关键.
11.(1)a=5,b=1;(2)t=15(s);(3)15,22.5.
【分析】(1)依据|a﹣5|+(b﹣1)2=0,即可得到a,b的值;
(2)依据∠ABO+∠BAO=90°,∠ABQ+∠BAM=180°,即可得到射线AM、射线BQ第一次互相垂直的时间;
(3)分两种情况讨论,依据∠ABQ'=∠BAM“时,BQ'∥AM“,列出方程即可得到射线AM、射线BQ互相平行时的时间.
【详解】解:(1)|a﹣5|+(b﹣1)2=0,
∴a﹣5=0,b﹣1=0,
∴a=5,b=1,
故答案为5,1;
(2)设至少旋转t秒时,射线AM、射线BQ互相垂直.
如图,设旋转后的射线AM、射线BQ交于点O,则BO⊥AO,
∴∠ABO+∠BAO=90°,
∵PQ∥MN,
∴∠ABQ+∠BAM=180°,
∴∠OBQ+∠OAM=90°,
又∵∠OBQ=t°,∠OAM=5t°,
∴t°+5t°=90°,
∴t=15(s);
(3)设射线AM再转动t秒时,射线AM、射线BQ互相平行.
如图,射线AM绕点A顺时针先转动18秒后,AM转动至AM'的位置,∠MAM'=18×5=90°,
分两种情况:
①当9<t<18时,∠QBQ'=t°,∠M'AM“=5t°,
∵∠BAN=45°=∠ABQ,
∴∠ABQ'=45°﹣t°,∠BAM“=5t﹣45°,
当∠ABQ'=∠BAM“时,BQ'∥AM“,
此时,45°﹣t°=5t﹣45°,
解得t=15;
②当18<t<27时,∠QBQ'=t°,∠NAM“=5t°﹣90°,
∵∠BAN=45°=∠ABQ,
∴∠ABQ'=45°﹣t°,∠BAM“=45°﹣(5t°﹣90°)=135°﹣5t°,
当∠ABQ'=∠BAM“时,BQ'∥AM“,
此时,45°﹣t°=135°﹣5t,
解得t=22.5;
【点睛】本题主要考查了平行线的性质,非负数的性质以及角的和差关系的运用,解决问题的关键是运用分类思想进行求解,解题时注意:若两个非负数的和为0,则这两个非负数均等于0.
12.(1)存在,t为3秒,BE的最小值为
(2)或
【分析】(1)根据“垂线段最短”可知:当时,为最小.过点作于点,先证,进而可依据“”判定和全等,从而得,,然后再求出,,进而可得出答案;
(2)先求出,,根据为等腰三角形,有以下三种情况:①当时,则,故此种情况不存在;②当时,则,则,据此得,则,由此即可求出的值;③当时,则,过点作于点,先证为等腰直角三角形,设,则,,,由此得,则,再由得,由此即可求出的值,综上所述即可得出答案.
【详解】(1)解:存在最小值.
根据“垂线段最短”可知:当时,为最小.
,
,
过点作于点,如图:
,
,
,
由旋转的性质得:,,
,
,
,
,,
,
在和中,
,
,
,,
,,
,
在中,,,
,
,
由勾股定理得:,
,,
运动的时间秒,的最小值为;
(2)由(1)可知:,
为的平分线,
,
当点从点出发时,点从点向点与点同时同速运动,
速度每秒1个单位长度,时间为秒,
,
当为等腰三角形时,有以下三种情况:
①当时,则,如图:
,
,这与三角形的任意一个外角都大于和它不相邻的一个内角相矛盾,此种情况不存在;
②当时,则,如图:
,
,
在中,,
,
,
解得:,
③当时,则,过点作于点,如图:
,
,
为等腰直角三角形,
设,
在中,,,则,
由勾股定理得:,
,
,
,
,
即:,
解得:.
综上所述:当为等腰三角形时,的值为或.
【点睛】此题主要考查了图形的旋转变换及性质,全等三角形的判定和性质,等腰三角形的性质,垂线段的性质,含有角的直角三角形的性质,熟练掌握全等三角形的判定和性质,理解垂线段最短时解答此题的关键,难点是分类讨论思想与方程思想在解题中的应用,漏解是解答此题的易错点.
13.(1)
(2)同意,图见解析,或
【分析】(1)由可得,再由,得到,最后求出的度数即可;
(2)由 可得,再求出度数.
【详解】(1)如图1当
所以
因为,
所以
因为
所以
(2)同意
如图2
当
所以
所以
综上或
【点睛】本题考查了平行线的性质,解决本题的关键是熟练掌握平行线的性质.
14.(1)150°;(2)EF2=BE2+FC2.(3).
【分析】(1)由△ACP′≌△ABP可得旋转角∠PAP′=60°,可得△APP′为等边三角形,根据勾股定理逆定理可证明△PP′C为直角三角形,根据∠APB=∠AP′C=∠AP′P+∠PP′C即可得答案;(2)如图2,把△ABE绕点A逆时针旋转90°得到△ACE′,由旋转的性质可得AE′=AE,CE′=BE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,根据角的和差关系可得∠EAF=∠E′AF,利用SAS可证明△EAF≌△E′AF,可得E′F=EF,根据等腰直角三角形的性质可得∠E′CF=90°,根据勾股定理即可得结论;(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,根据含30°角的直角三角形的性质及勾股定理可求出AB、BC的长,根据旋转的性质可得∠A′BC=90°,△BOO′是等边三角形,由∠AOC=∠COB=∠BOA=120°,利用平角的定义可证明C、O、A′、O′四点共线,利用勾股定理求出A′C的长即可得答案.
【详解】(1)∵△ACP′≌△ABP,
∴AP′=AP=3、CP′=BP=4、∠AP′C=∠APB,
由题意知旋转角∠PAP′=60°,
∴△APP′为等边三角形,
∴P′P=AP=3,∠AP′P=60°,
∵P′C=PB=4,PC=5,
∴PC2=P′C2+P′P2,
∴△PP′C为直角三角形,且∠PP′C=90°,
∴∠APB=∠AP′C=∠AP′P+∠PP′C=60°+90°=150°.
故答案为150°
(2)如图2,把△ABE绕点A逆时针旋转90°得到△ACE′,
由旋转的性质得,AE′=AE,CE′=BE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,
∵∠EAF=45°,
∴∠E′AF=∠EAE′-∠EAF=45°,
∴∠EAF=∠E′AF,
在△EAF和△E′AF中,
∴△EAF≌△E′AF(SAS),
∴E′F=EF,
∵∠CAB=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠E′CF=45°+45°=90°,
由勾股定理得,E′F2=CE′2+FC2,
即EF2=BE2+FC2.
(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,
∵在Rt△ABC中,∠ACB=90°,AC=1,∠ABC=30°,
∴AB=2,
∴BC=,
∵△AOB绕点B顺时针方向旋转60°,∠ABC=30°,
∴∠A′BC=∠ABC+60°=30°+60°=90°,
∵∠C=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO,
∴△BOO′是等边三角形,
∴BO=OO′,∠BOO′=∠BO′O=60°,
∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°,
∴C、O、A′、O′四点共线,
在Rt△A′BC中,A′C=,
∴OA+OB+OC=A′O′+OO′+OC=A′C=.
【点睛】本题考查了旋转的性质、等边三角形的判定与性质、等腰直角三角形的性质及含30°角的直角三角形的性质,熟练掌握旋转的性质,正确得出对应边和对应角是解题关键.
15.(1)3,1
(2)
(3)
【分析】(1)根据二元一次方程的解,,为正整数,即可求解;
(2)设运动时间为,依题意,,则,,过点作,则,根据平行线的性质得出,根据已知条件得出,建立方程求得,进而得出,根据,进而即可求解;
(3)先转动30秒,射线才开始转动,当到达之前,当从返回且到达前,根据平行线的性质,列出方程,解方程即可求解.
【详解】(1)解:,,为正整数,
,
,;
(2)设运动时间为,
由题意得,,则,,
过点作,则,
,
,
,
,
,
,
,
,
,
,
解得:,
,
;
(3)依题意,线先转动30秒,射线才开始转动,
当到达之前,当时,则,
,
解得:;
当从返回且到达前,当时,则,
,
解得:.
【点睛】本题考查了二元一次方程的解,平行线的性质与判定,一元一次方程的应用,熟练掌握平行线的性质是解题的关键.
16.(1)
(2)①当旋转时间为3或21秒时,成立;②旋转的时间是25秒
【分析】(1)根据平角即可得到结论;
(2)①如解图1,根据平行线的性质得到,求得,于是得到结论;如解图2,根据平行线的性质得到,根据三角形的内角和得到,求得,于是得到结论;②设旋转的时间为t秒,由题知,,根据周角得到,列方程即可得到结论.
【详解】(1)∵,
∴,
故答案为:;
(2)①如解图1,此时,成立,
∵,
∴,
∵,
∴,
∴,
∵转速为秒,
∴旋转时间为3秒;
如解图2,,
∵,
∴,
∵,
∴,
∴,
∵三角板绕点P逆时针旋转D的角度为,
∵转速为秒,
∴旋转时间为21秒,
综上所述,当旋转时间为3或21秒时,成立;
②设旋转的时间为t秒,由题知,,
∴,
∴,
当,即,
解得:,
∴当,旋转的时间是25秒.
【点睛】本题考查了旋转的性质,平行线的性质,三角形的内角和,识别图形是解题的关键.
17.(1);
(2).
【分析】(1)利用证明,推出,即可得到;
(2)利用旋转的性质以及矩形的判定定理得到四边形是矩形,根据矩形的性质即可求解.
【详解】(1)证明:∵正方形,
∴,.
∵,
∴.
∴.
∴.
又∵,
∴.
在△AED和△BFA中,
∵,,.
∴.
∴.
∵,
∴.
(2)解:如图,
由题设得,
∴,
由旋转的性质知:,,
∴,
∴.
∴四边形为平行四边形.
又∵,
∴四边形是矩形.
∴.
【点睛】此题考查了正方形的性质,全等三角形的判定与性质,矩形的判定与性质,以及旋转的性质,熟练掌握判定与性质是解本题的关键.
18.(1)
(2)
(3)或
【分析】(1)根据平行线的性质得出,得出,即可求解.
(2)设交于点,则,过点作,推出.根据平行线的性质得出则.求出,即可求解;
(3)根据题意,进行分类讨论:①当点在上方时,②当点在下方时,正确画出图形,根据平行线的性质求解即可.
【详解】解:(1)∵,
.
又,
,
.
(2)如图1,设交于点,则,过点作,
∵,
.
.
.
又,
,
.
(3)或.
如图2,交于点,当点在上方时,
设,则,
∴,
解得.
∴;
如图3,延长交于点,当点在下方时,
设,则,
∴,
解得,
∴.
综上所述,的度数为或.
【点睛】本题主要考查了平行线的性质,解题的关键是掌握平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.
19.(1)105°
(2)150°
(3)75°或255°
【分析】(1)根据三角形的内角和即可求解;
(2)根据角平分线的定义可得,从而得出,最后根据平行线的性质即可求解;
(3)根据题意,画出图形,进行分类讨论:①在上方时,设与相交于F,②当在的下方时,设直线与相交于F.
【详解】(1)解:∵,,
∴在中,.
故答案为:.
(2)∵平分,
∴,
∴,
∴,
∴;
(3)如图1,在上方时,设与相交于F,
∵,
∴,
在中,,
,
,
当在的下方时,设直线与相交于F,
∵,
∴,
在中,,
∴旋转角为,
综上所述,当边旋转或时,边恰好与边平行.
【点睛】本题考查了旋转的性质,三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,直角三角形两锐角互余的性质,熟记各性质并熟悉三角板的度数特点是解题的关键.
20.知识探究:,理由见解析;拓展探究:EM=EN,理由见解析;迁移运用:见解析
【分析】知识探究:根据正方形的性质可得,平分,再根据垂直定义可得,从而可得四边形是矩形,然后利用矩形的性质可得,从而利用角平分线的性质即可解答.
拓展探究:过点E作,垂足为P,过点E作,垂足为Q,根据垂直定义可得,再根据正方形的性质可得,平分,从而可得四边形是矩形,进而可得,然后利用等式的性质可得,再利用角平分线的性质可得,从而证明,最后利用全等三角形的性质即可解答;
迁移运用:连接,根据正方形的性质可得,平分,从而可得,然后证明,从而可得,进而可得,最后利用等腰三角形的三线合一性质即可解答.
【详解】解:知识探究:,
理由:∵四边形是正方形,
∴,平分,
∵,
∴,
∵,
∴四边形是矩形,
∴,
∴;
拓展探究:,
理由:过点E作,垂足为P,过点E作,垂足为Q,
∴,
∵四边形是正方形,
∴,平分,
∴四边形是矩形,
∴,
∵,
∴,
∴,
∵平分,,,
∴,
∴,
∴;
迁移运用:连接,
∵四边形是正方形,
∴,平分,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴H是线段的中点.
【点睛】本题考查了旋转的性质,正方形的性质,全等三角形的判定与性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
21.(1)证明见解析
(2)不同意,理由见解析
(3)
【分析】(1)由四边形与均为正方形,得,,,,进而有,于是即可证明结论成立;
(2)证明四边形的面积总等于正方形面积的即可;
(3)由(2)即可得解.
【详解】(1)证明:四边形与均为正方形,
,,,,
,
,
即,
.
(2)解:不同意,理由:
由(1)可知:,
,
,
即当正方形绕点O转动时,四边形的面积总等于正方形面积的.
(3)解:∵,正方形的边长为a,
∴,
故答案为.
【点睛】本题主要考查了正方形的性质,全等三角形的判定和性质,得到是解题的关键.
22.(1)130°;(2)∠AOD与∠COE的差不发生变化,为30°;(3)∠AOE=131.25°或175°.
【分析】(1)求出∠COE的度数,即可求出答案;
(2)分为两种情况,根据∠AOC=90°和∠DOE=60°求出即可;
(3)根据∠AOE=7∠COD、∠DOE=60°、∠AOC=90°求出即可.
【详解】(1)∵OC⊥AB,
∴∠AOC=90°,
∵OD在OA和OC之间,∠COD=20°,∠EOD=60°,
∴∠COE=60°-20°=40°,
∴∠AOE=90°+40°=130°,
故答案为130°;
(2)在△ODE旋转过程中,∠AOD与∠COE的差不发生变化,
有两种情况:①如图1、∵∠AOD+∠COD=90°,∠COD+∠COE=60°,
∴∠AOD-∠COE=90°-60°=30°,
②如图2、∵∠AOD=∠AOC+∠COD=90°+∠COD,∠COE=∠DOE+∠DOC=60°+∠DOC,
∴∠AOD-∠COE=(90°+∠COD)-(60°+∠COD)=30°,
即△ODE在旋转过程中,∠AOD与∠COE的差不发生变化,为30°;
(3)如图1、∵∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,
∴90°+60°-∠COD=7∠COD,
解得:∠COD=18.75°,
∴∠AOE=7×18.75°=131.25°;
如图2、∵∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,
∴90°+60°+∠COD=7∠COD,
∴∠COD=25°,
∴∠AOE=7×25°=175°,
即∠AOE=131.25°或175°.
【点睛】本题考查了角的有关计算的应用,能根据题意求出各个角的度数是解此题的关键.注意分类思想的运用.
23.(1),理由见解析
(2)见解析
(3)见解析
【分析】(1)先根据旋转的性质得,,则可判断为等边三角形,所以,,再利用为等边三角形得到,,则可得到;
(2)通过证明得到;
(3)先判断为等边三角形得到,,再与(2)的证明方法一样证明得到,所以,加上,从而可判断四边形是平行四边形.
【详解】(1)解:.
理由如下:逆时针旋转得到,
,,
为等边三角形,
,,
为等边三角形,
,,
,,
;
(2)证明:在和中,
,
,
;
(3)证明:顺时针旋转得到,
,,
为等边三角形,
,,
为等边三角形,
,,
,,
;
在和中,
,
,
,
,
,
四边形是平行四边形.
【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质、全等三角形的判定与性质和平行四边形的判定.
24.探究:成立,证明见解析;应用:①45;②.
【分析】探究:根据旋转的性质得出,然后利用证明即可;
应用:①根据全等三角形的性质可得答案;
②利用勾股定理求出,可得的长,根据全等三角形的性质可得的长,求出,根据勾股定理可得答案.
【详解】探究:成立,
证明:∵和都是等腰直角三角形,
∴,,
∵将绕点A逆时针旋转,
∴,
在与中,,
∴,
∴;
应用:①∵是等腰直角三角形,
∴,
同探究可得:,
∴,
故答案为:45;
②∵在中,,
∴,
∴,
∵
∴,
∵,,
∴,
∴,
∴.
【点睛】本题是几何变换综合题,主要考查了等腰直角三角形的性质,旋转的性质,全等三角形的判定与性质,勾股定理,证明是解题的关键.
25.(1)
(2)
(3)或或或
【分析】(1)先计算的度数,再根据角平分线的定义和旋转的速度可得的值;
(2)分别表示与的度数,相减可得数量关系;
(3)分四种情况讨论:分别和三边平行,还有,计算旋转角并根据速度列方程可得结论.
【详解】(1)解:如图2,,,
,
平分,
,
,
答:此时的值是;
(2)当旋转至的内部时,如图3,与的数量关系是:;
理由是:由旋转得:,
,,
;
(3)分四种情况:
①当时,如图4,,
;
②当时,如图5,则,
,
;
③当时,如图6,则,
,
;
④当时,如图7,
,
,
;
综上,的值是或或或.
故答案为:或或或.
【点睛】本题考查了平行线的性质,角平分线的定义,是典型的实际操作问题,将两个三角板按照题意进行摆放,旋转,清楚每一时刻各个角的度数是多少和各角之间的关系.
26.(1)3;21
(2)当t为6或15或24时,有两个内角相等
(3)105
【分析】(1)由平行和垂直求出旋转角,结合旋转速度求出旋转时间;
(2)画出图形,分类讨论,①;②;③,求出旋转角,再求出值;
(3)找出与,,,有关的数量关系,再把无关的角消去,得出结论.
【详解】(1)解:如图(1),当时,
平分,,
,
又为的一个外角,
,
;
如图(2),当时,
,
,
,
,
.
故答案为:3;21.
(2)①如图(3),当时,
,
,
;
②如图(4),当时,
,,
,
;
③如图(5),当时,
,
,
综上所述:当为6或15或24时,有两个内角相等.
(3)是为定值105,理由如下:
是的一个外角,是的一个外角,
,,
又,,
,
,
.
【点睛】本题以求三角形旋转时间为背景,考查了学生对图形的旋转变换、平行的性质、垂直的性质和求等腰三角形内角的掌握情况,第(2)问分情况讨论是解决问题的关键,第(3)问找到三个角之间的关系是关键.
27.(1),理由见解析
(2)A、;B、
【分析】(1)由“”可证,可得;
(2)、由等腰三角形的性质可求,由全等三角形的性质可求,即可求解;、分两种情况讨论,由等腰三角形的性质和全等三角形的性质可求解.
【详解】(1)解:,理由如下:
,,
,
将线段绕点按逆时针方向旋转得到线段,
,,
,
在和中,
,
,
;
(2)、如图:
,,
,
,
,
,
;
、如图,当点在线段上时,
,,
,
,
,
,
;
如图,当点在线段上时,
,,
,
,
,
,
;
如图,当点在线段上时,
同理可求,
综上所述:或.
【点睛】本题考查了旋转的性质,等腰三角形的性质,全等三角形的判定和性质,利用分类讨论思想解决问题是解题的关键.
28.(1)∠EFB=15°;(2)①30°;②存在,图见解析,∠ECB=120°、165°、150°、60°或15°.
【分析】(1)根据直角三角形内角和的性质即可得到答案;
(2)①根据平行线的性质即可得到答案;
②分5种情况讨论,根据平行线的性质进行计算,即可得到答案.
【详解】解:(1)∵∠A=30°,∠CDE=45°,
∴∠ABC=90°﹣30°=60°,∠E=90°﹣45°=45°,
∴∠EFB=∠ABC﹣∠E=60°﹣45°=15°;
(2)①∵CD∥AB,
∴∠ACD=∠A=30°,
∵∠ACD+∠ACE=∠DCE=90°,
∠ECB+∠ACE=∠ACB=90°,
∴∠ECB=∠ACD=30°;
②如图1,CE∥AB,∠ACE=∠A=30°,
∠ECB=∠ACB+∠ACE=90°+30°=120°;
如图2,DE∥AB时,延长CD交AB于F,
则∠BFC=∠D=45°,
在△BCF中,∠BCF=180°﹣∠B﹣∠BFC,
=180°﹣60°﹣45°=75°,
∴∠ECB=∠BCF+∠ECF=75°+90°=165°;
如图3,CD∥AB时,∠BCD=∠B=60°,
∠ECB=∠BCD+∠EDC=60°+90°=150°;
如图4,CE∥AB时,∠ECB=∠B=60°,
如图5,DE∥AB时,∠ECB=60°﹣45°=15°.
【点睛】本题考查三角形内角和的性质、平行线的性质,解题的关键是掌握三角形内角和的性质、平行线的性质,分5种情况讨论解答.
29.(1)4(2)
【分析】(1)根据正方形的性质得出,,,推出,证出,即可得出结果;
(2)发生变化,对旋转角分情况讨论即可.
【详解】解:(1)连接,,
四边形和四边形都是正方形,
,,,
,
在与中,
,
,
四边形的面积等于三角形的面积,
即重叠部分面积不变,总是等于正方形面积的,
;
(2)设等边绕着点的旋转角为,等边的边长等于4,则高为,
①如图,当经过点时,若此时开始旋转,,重叠部分的形状为直角三角形,
,
②如图,当旋转至图中位置时,,重叠部分的形状为菱形,
,
③如图,当旋转至图中位置时,,重叠部分的形状为等边三角形,
,
④如图,当旋转至图中位置时,,重叠部分的形状为直角三角形,
,
综上所述,这两个等边三角形重叠部分的面积是变化的,的变化范围是.
【点睛】本题考查正方形的性质和等边三角形的性质,找出面积之间的关系是解题关键.
30.问题发现:①③④
数学思考:,,理由见解析
拓展应用:
【分析】●问题发现:由等腰三角形的性质判断①,作辅助线构造三角形判断②,由过一点有且只有一条直线垂直于已知直线判断③,由③的结论可以判断④;
●数学思考:连接,,由是等边三角形可得,,,,然后证明,进而证明结论;
●拓展应用:分两种情况利用勾股定理解题即可.
【详解】解:●问题发现:
∵是边的中点,是等边三角形,
∴,
又∵,
∴,所以①正确;
过D作交于点G,
∴
∵和都是等边三角形,
∴,
∴,
∴四边形为平行四边形,
∴,所以②不正确;
连接,
∵和都是等边三角形,
∴,
∵
∴,
∴三点共线,即,所以③正确;
由③可知整个图形关于直线成轴对称图形,所以④正确;
故答案为:①③④.
●数学思考:,.理由如下:
连接,,由图1,,,
可得.绕着点旋转,
仍然成立.∵是等边三角形,
∴,.
∴.
同理,,.
∴,.
∴.
∴.
∴,.
延长交于点,交于点,
又,∴.
∴.
∴.
●拓展应用
当时,∵,∴,,三点共线.
如备用图1,
设,则.∵,
∴在中,.
解之得:.又,
∴
即.
如备用图2.
设,则.∵,
∴在中,.
解之得:.
又,∴
即.
综上所述,.
【点睛】本题考查等边三角形的性质,勾股定理,旋转的性质,相似三角形的判定和性质,掌握等边三角形的性质和旋转的性质是解题的关键.
答案第1页,共2页
答案第1页,共2页
同课章节目录
