4.3 相似多边形 课件(共21张PPT)2023-2024学年度北师大版数学九年级上册
文档属性
| 名称 | 4.3 相似多边形 课件(共21张PPT)2023-2024学年度北师大版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-07 09:55:49 | ||
图片预览






文档简介
(共21张PPT)
第四章 图形的相似
3 相似多边形
学习目标
学习目标
1.理解相似的概念,掌握多边形相似的判定方法;
2.掌握并运用相似形的性质;
3.在探索相似多边形本质特征的过程中,进一步发展自己归纳、类比、反思、交流等方面的能力,提高数学思维水平,体会反例的作用.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
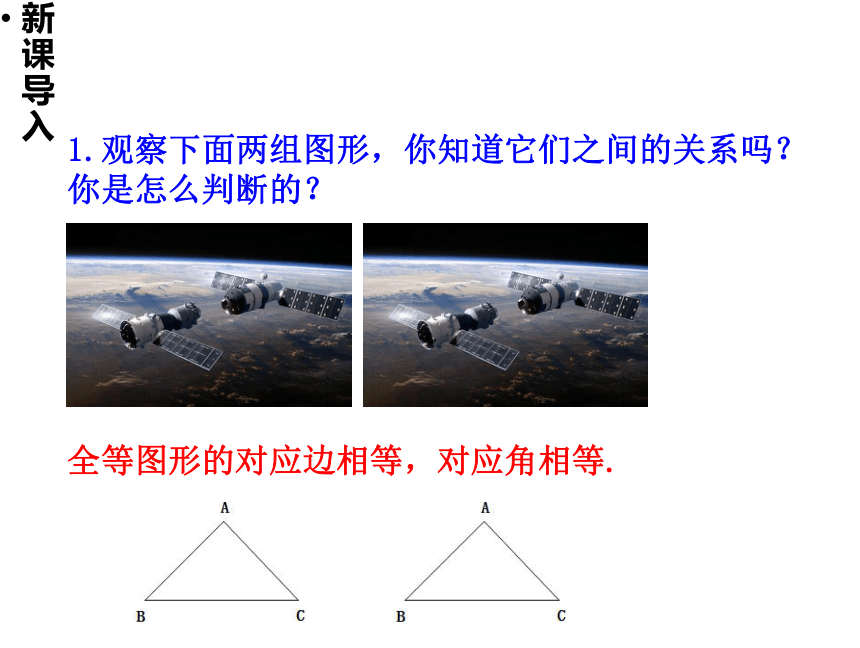
1.观察下面两组图形,你知道它们之间的关系吗?
你是怎么判断的?
全等图形的对应边相等,对应角相等.
新课导入
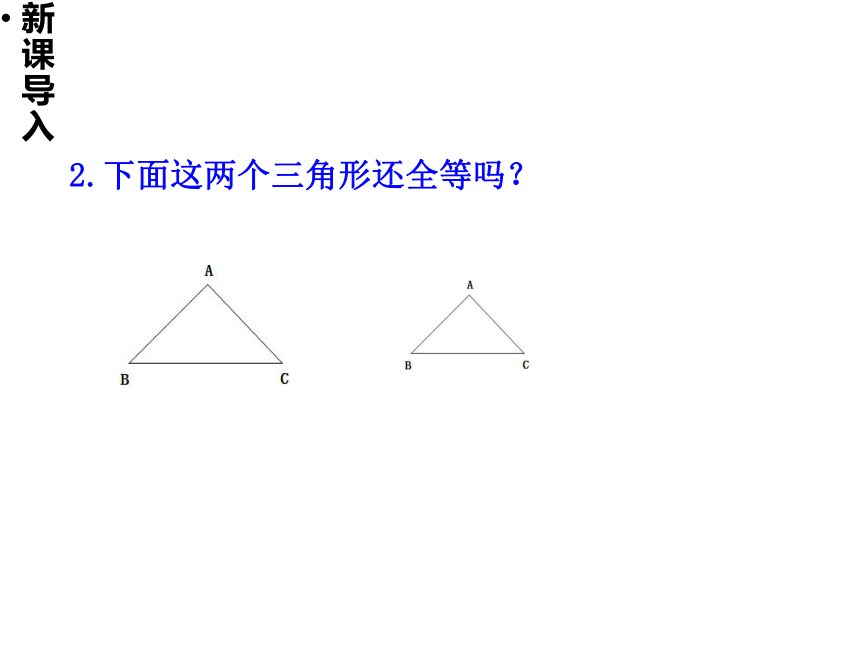
2.下面这两个三角形还全等吗?
讲授新知
贰
讲授新知
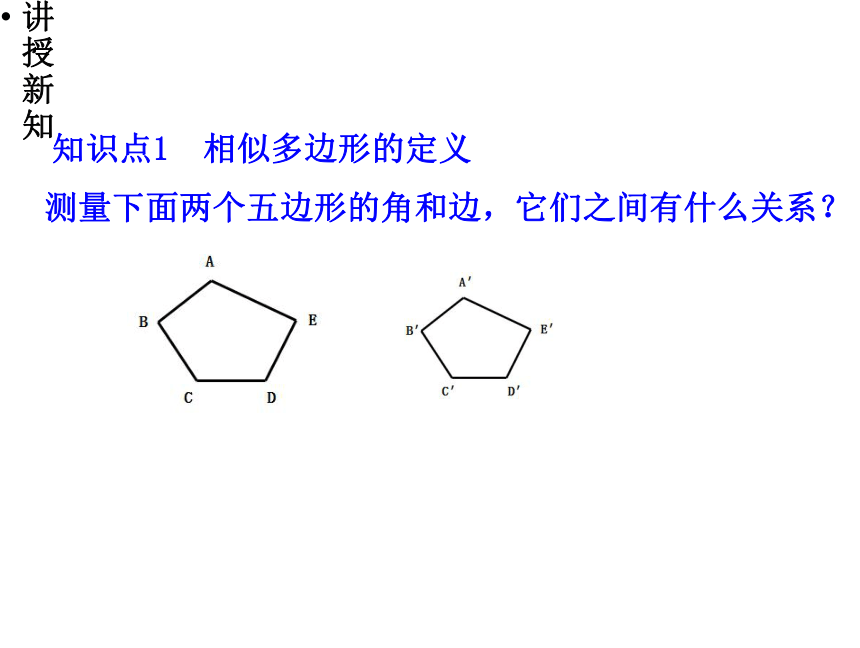
知识点1 相似多边形的定义
测量下面两个五边形的角和边,它们之间有什么关系?
讲授新知
(1)各角对应相等,各边对应成比例的两个多边形
叫做相似多边形.相似多边形对应边的比叫做相似比;
(2)相似多边形的记法:用“∽”符号表示相似,
如五边形ABCDE与五边形A'B'C'D'E'相似,
记为“五边形ABCDE∽五边形A'B'C'D'E'”,
讲授新课
知识点2 多边形相似的判定
下列结论正确的是( )
A.所有的矩形都相似 B.所有的菱形都相似
C.所有的正方形都相似 D.所有的正多边形都相似
C
各角对应相等,各边对应成比例的两个多边形相似
范例应用
例1 一块长3m,宽1.5m的矩形黑板ABCD,如图所示,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的矩形ABCD与矩形相似吗?为什么?
解:不相似;
内边缘的矩形ABCD长AD=300 cm,宽AB=150 cm,
外边缘的矩形长A'D'=315 cm,宽A'B'=165 cm,
∵=,=,
≠,
所以内外边缘所成的两个矩形不相似.
讲授新课
知识点3 相似多边形的性质
如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠H的度数为( )
A.70° B.80° C.110° D.120°
D
相似多边形的对应角相等,对应边成比例.
范例应用
例2 如图,四边形ABCD与四边形EFGH相似,∠A=70°,
∠B=80°,∠H=150°,AD=8,EF=5,EH=6,
求∠G和AB的长.
解:∵四边形ABCD∽四边形EFGH,
∠A=70°,∠B=80°,AD=8,EF=5,EH=6,
∴∠E=∠A=70°,∠F=∠B=80°, =,
即 =,
∴∠G=360°﹣∠E﹣∠H﹣∠F=60°.AB=.
当堂训练
叁
当堂训练
1.下列四组图形中,不是相似图形的是( )
A. B. C. D.
2.下列各组图形中,不一定相似的是( )
A.两个矩形
B.两个等腰直角三角形
C.各有一个角是50°的两个直角三角形
D.各有一个角是100°的两个等腰三角形
D
A
当堂训练
3.如图所示,一张矩形纸片ABCD的长BC=x,宽AB=1,
沿EF将矩形纸片ABCD剪成大小相同的两个小矩形,若剩
下的矩形ECDF与原矩形ABCD相似,则原矩形的长x的值
为 _______.
4.如图,四边形ABCD∽四边形A′B′C′D′,若∠B=65°,∠C=82°,∠A′=110°,则∠D=______°.
103
当堂训练
5.如图,四边形ABCD的对角线相交于点O,A′,B′,
C′,D′分别是OA,OB,OC,OD的中点,试判断四边
形ABCD与四边形A′B′C′D′是否相似,并说明理由.
解:∵A′,B′分别是OA,OB的中点,
∴∠OA′B′=∠OAB,=,
同理,∠OA′D′=∠OAD,=,
∴∠B′A′D′=∠BAD,=,
同理,∠B′A′D′=∠BAD,∠A′D′C′=∠ADC,
∠D′C′B′=∠DCB,∠C′B′A′=∠CBA,
===,
∴四边形ABCD∽四边形A′B′C′D′.
课堂小结
肆
课堂小结
1.相似多边形的概念及判定方法
2.相似多边形的性质
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学采取合理的方式,搜集整理与本节课有关的“好题”,被选中的同学下节课为全班展示。
谢
谢
第四章 图形的相似
3 相似多边形
学习目标
学习目标
1.理解相似的概念,掌握多边形相似的判定方法;
2.掌握并运用相似形的性质;
3.在探索相似多边形本质特征的过程中,进一步发展自己归纳、类比、反思、交流等方面的能力,提高数学思维水平,体会反例的作用.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
1.观察下面两组图形,你知道它们之间的关系吗?
你是怎么判断的?
全等图形的对应边相等,对应角相等.
新课导入
2.下面这两个三角形还全等吗?
讲授新知
贰
讲授新知
知识点1 相似多边形的定义
测量下面两个五边形的角和边,它们之间有什么关系?
讲授新知
(1)各角对应相等,各边对应成比例的两个多边形
叫做相似多边形.相似多边形对应边的比叫做相似比;
(2)相似多边形的记法:用“∽”符号表示相似,
如五边形ABCDE与五边形A'B'C'D'E'相似,
记为“五边形ABCDE∽五边形A'B'C'D'E'”,
讲授新课
知识点2 多边形相似的判定
下列结论正确的是( )
A.所有的矩形都相似 B.所有的菱形都相似
C.所有的正方形都相似 D.所有的正多边形都相似
C
各角对应相等,各边对应成比例的两个多边形相似
范例应用
例1 一块长3m,宽1.5m的矩形黑板ABCD,如图所示,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的矩形ABCD与矩形相似吗?为什么?
解:不相似;
内边缘的矩形ABCD长AD=300 cm,宽AB=150 cm,
外边缘的矩形长A'D'=315 cm,宽A'B'=165 cm,
∵=,=,
≠,
所以内外边缘所成的两个矩形不相似.
讲授新课
知识点3 相似多边形的性质
如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠H的度数为( )
A.70° B.80° C.110° D.120°
D
相似多边形的对应角相等,对应边成比例.
范例应用
例2 如图,四边形ABCD与四边形EFGH相似,∠A=70°,
∠B=80°,∠H=150°,AD=8,EF=5,EH=6,
求∠G和AB的长.
解:∵四边形ABCD∽四边形EFGH,
∠A=70°,∠B=80°,AD=8,EF=5,EH=6,
∴∠E=∠A=70°,∠F=∠B=80°, =,
即 =,
∴∠G=360°﹣∠E﹣∠H﹣∠F=60°.AB=.
当堂训练
叁
当堂训练
1.下列四组图形中,不是相似图形的是( )
A. B. C. D.
2.下列各组图形中,不一定相似的是( )
A.两个矩形
B.两个等腰直角三角形
C.各有一个角是50°的两个直角三角形
D.各有一个角是100°的两个等腰三角形
D
A
当堂训练
3.如图所示,一张矩形纸片ABCD的长BC=x,宽AB=1,
沿EF将矩形纸片ABCD剪成大小相同的两个小矩形,若剩
下的矩形ECDF与原矩形ABCD相似,则原矩形的长x的值
为 _______.
4.如图,四边形ABCD∽四边形A′B′C′D′,若∠B=65°,∠C=82°,∠A′=110°,则∠D=______°.
103
当堂训练
5.如图,四边形ABCD的对角线相交于点O,A′,B′,
C′,D′分别是OA,OB,OC,OD的中点,试判断四边
形ABCD与四边形A′B′C′D′是否相似,并说明理由.
解:∵A′,B′分别是OA,OB的中点,
∴∠OA′B′=∠OAB,=,
同理,∠OA′D′=∠OAD,=,
∴∠B′A′D′=∠BAD,=,
同理,∠B′A′D′=∠BAD,∠A′D′C′=∠ADC,
∠D′C′B′=∠DCB,∠C′B′A′=∠CBA,
===,
∴四边形ABCD∽四边形A′B′C′D′.
课堂小结
肆
课堂小结
1.相似多边形的概念及判定方法
2.相似多边形的性质
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学采取合理的方式,搜集整理与本节课有关的“好题”,被选中的同学下节课为全班展示。
谢
谢
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
