6.2.1反比例函数的图象 课件(共23张PPT)2023-2024学年度北师大版数学九年级上册
文档属性
| 名称 | 6.2.1反比例函数的图象 课件(共23张PPT)2023-2024学年度北师大版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-07 10:46:19 | ||
图片预览







文档简介
(共23张PPT)
第六章 反比例函数
2 反比例函数的图象与性质
第1课时 反比例函数的图象
学习目标
学习目标
1.进一步熟悉作函数图象的主要步骤,会作反比例函数的图象;
2.体会函数的三种表示方法的互相转换,对函数进行认识上的整合;
3.逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的图象特点.
4.训练学生的概括、总结能力.增强他们对数学学习的好奇心与求知欲.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
1.下列函数中哪些是反比例函数
①y=3x-1;②y=2;③y=;④y=;
⑤y=3x;⑥y=-;⑦y=;⑧y=.
2.一次函数的一般形式是_________(k__0),其图象
是____. 反比例函数的一般形式是________(k___0).
3.作函数图象的一般步骤是_______,______,_______.
y=kx+b
≠
直线
y=
≠
列表
描点
连线
讲授新知
贰
讲授新知
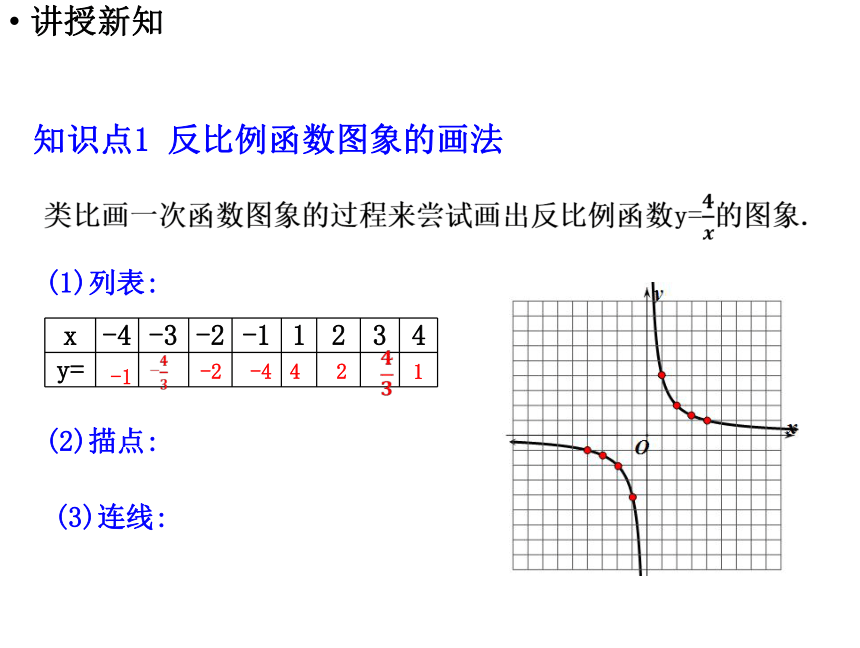
知识点1 反比例函数图象的画法
类比画一次函数图象的过程来尝试画出反比例函数y=的图象.
(1)列表:
x -4 -3 -2 -1 1 2 3 4
y=
(2)描点:
(3)连线:
-1
-
-2
-4
4
2
1
讲授新知
图象分别都是由两支曲线组成,因此称反比例函数的图象为双曲线
讲授新课
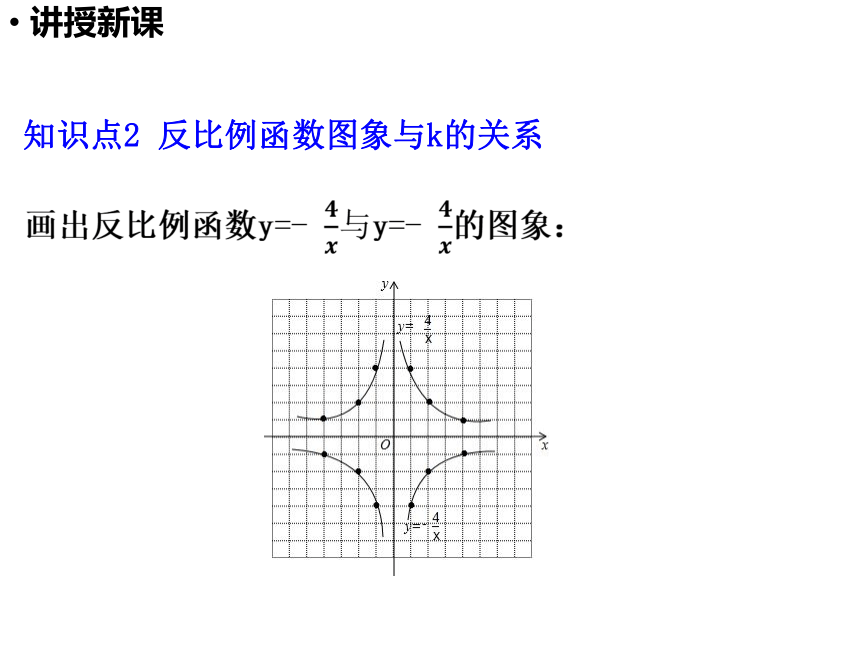
知识点2 反比例函数图象与k的关系
画出反比例函数y=- 与y=- 的图象:
讲授新课
当k>0时,两支双曲线分别位于第一、三象限内;
当k<0时,两支双曲线分别位于第二、四象限内.
范例应用
例1 在同一平面直角坐标系中,画出下列函数的图象,
并比较它们的异同
(1)y=(2)y=-
相同点:都是双曲线,无限接近坐标轴,
但和坐标轴永不相交,
不同点:y=图象在一、三象限,
y=-图象在二、四象限
讲授新课
知识点3 双曲线的对称性
对于反比例函数y的图象的对称性叙述错误的是( )
A.关于原点中心对称 B.关于直线y=x对称
C.关于直线y=﹣x对称 D.关于x轴对称
D
讲授新课
反比例函数图象(双曲线)既是轴对称图形,
对称轴为直线y=x和y=﹣x,
又是中心对称图形,对称中心是原点.
范例应用
例2 正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2) B.(﹣2,﹣1)
C.(1,2) D.(2,1)
A
当堂训练
叁
当堂训练
1.函数的图象为( )
A.直线 B.抛物线 C.双曲线 D.线段
2.1.反比例函数y=的图象两支分布在第二、四象限,
则点(m,m-2)在( )
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
C
C
当堂训练
3.反比例函数y=与一次函数y=kx﹣k(k≠0)在同一
平面直角坐标系中的图象可能是( )
A. B.
C. D.
D
当堂训练
4.如图,在平面直角坐标系中,正方形的中心在原点O,
且正方形的一组对边与x轴平行,点P(2a,a)是反比
例函数y=的图象与正方形的一个交点,则图中阴影部分
的面积是______.
4
当堂训练
5.已知反比例函数y=(k>0)的图象如图.你认为利用
怎样的图形运动就能得到反比例函数y(k>0)的图象?
请画出这个图象.
课堂小结
肆
课堂小结
1.反比例函数的图象及其特点
2.双曲线的对称性
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学采取合理的方式,搜集整理与本节课有关的“好题”,被选中的同学下节课为全班展示。
谢
谢
第六章 反比例函数
2 反比例函数的图象与性质
第1课时 反比例函数的图象
学习目标
学习目标
1.进一步熟悉作函数图象的主要步骤,会作反比例函数的图象;
2.体会函数的三种表示方法的互相转换,对函数进行认识上的整合;
3.逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的图象特点.
4.训练学生的概括、总结能力.增强他们对数学学习的好奇心与求知欲.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
1.下列函数中哪些是反比例函数
①y=3x-1;②y=2;③y=;④y=;
⑤y=3x;⑥y=-;⑦y=;⑧y=.
2.一次函数的一般形式是_________(k__0),其图象
是____. 反比例函数的一般形式是________(k___0).
3.作函数图象的一般步骤是_______,______,_______.
y=kx+b
≠
直线
y=
≠
列表
描点
连线
讲授新知
贰
讲授新知
知识点1 反比例函数图象的画法
类比画一次函数图象的过程来尝试画出反比例函数y=的图象.
(1)列表:
x -4 -3 -2 -1 1 2 3 4
y=
(2)描点:
(3)连线:
-1
-
-2
-4
4
2
1
讲授新知
图象分别都是由两支曲线组成,因此称反比例函数的图象为双曲线
讲授新课
知识点2 反比例函数图象与k的关系
画出反比例函数y=- 与y=- 的图象:
讲授新课
当k>0时,两支双曲线分别位于第一、三象限内;
当k<0时,两支双曲线分别位于第二、四象限内.
范例应用
例1 在同一平面直角坐标系中,画出下列函数的图象,
并比较它们的异同
(1)y=(2)y=-
相同点:都是双曲线,无限接近坐标轴,
但和坐标轴永不相交,
不同点:y=图象在一、三象限,
y=-图象在二、四象限
讲授新课
知识点3 双曲线的对称性
对于反比例函数y的图象的对称性叙述错误的是( )
A.关于原点中心对称 B.关于直线y=x对称
C.关于直线y=﹣x对称 D.关于x轴对称
D
讲授新课
反比例函数图象(双曲线)既是轴对称图形,
对称轴为直线y=x和y=﹣x,
又是中心对称图形,对称中心是原点.
范例应用
例2 正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2) B.(﹣2,﹣1)
C.(1,2) D.(2,1)
A
当堂训练
叁
当堂训练
1.函数的图象为( )
A.直线 B.抛物线 C.双曲线 D.线段
2.1.反比例函数y=的图象两支分布在第二、四象限,
则点(m,m-2)在( )
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
C
C
当堂训练
3.反比例函数y=与一次函数y=kx﹣k(k≠0)在同一
平面直角坐标系中的图象可能是( )
A. B.
C. D.
D
当堂训练
4.如图,在平面直角坐标系中,正方形的中心在原点O,
且正方形的一组对边与x轴平行,点P(2a,a)是反比
例函数y=的图象与正方形的一个交点,则图中阴影部分
的面积是______.
4
当堂训练
5.已知反比例函数y=(k>0)的图象如图.你认为利用
怎样的图形运动就能得到反比例函数y(k>0)的图象?
请画出这个图象.
课堂小结
肆
课堂小结
1.反比例函数的图象及其特点
2.双曲线的对称性
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学采取合理的方式,搜集整理与本节课有关的“好题”,被选中的同学下节课为全班展示。
谢
谢
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
