2023-2024学年度北师大版数学九年级上册6.3 反比例函数的应用 课件(共20张PPT)
文档属性
| 名称 | 2023-2024学年度北师大版数学九年级上册6.3 反比例函数的应用 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-07 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第六章 反比例函数
3 反比例函数的应用
学习目标
学习目标
1.能根据实际问题中的条件确定反比例函数的表达式,会画出它的图象,能根据图象指出函数值随自变量的变化情况.
2.能通过探索实际问题列出函数表达式,利用反比例函数的性质解释实际问题,细心体会图象在解决问题时的作用.
3.通过对实际问题的分析与解决,让学生体验数学的价值,培养学生对数学的兴趣.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
1.什么是反比例函数
2.反比例函数的图象有什么性质
反比例函数:当k>0时,两支曲线分别在________象限,
在每一象限内,y的值随x的增大而______.
当k<0时,两支曲线分别在___________象限,
在每一象限内,y的值随x的增大而_____.
如果两个变量x、y之间的对应关系可以表示成y=
一、三
减小
二、四
增大
讲授新知
贰
讲授新知
知识点1 反比例函数的实际应用
某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为
了安全、迅速通过这片湿地,他们沿着前进路线铺垫了若干块木板,
构筑成一条临时通道,从而顺利完成了任务.你能解释他们这样做的
道理吗 当人和木板对湿地的压力一定时随着木板面积S(m2)的变化,
人和木板对地面的压强p(Pa)将如何变化 如果人和木板对湿地地面
的压力合计600 N,
(1)用含S的代数式表示p,p是S的反比例函数吗 为什么
(2)当木板面积为0.2 时,压强是多少
解:(1)p=,p是S的反比例函数.
(2)当S=0.2 时,p==3 000(Pa).
当木板面积为0.2 时,压强是3 000 Pa.
讲授新知
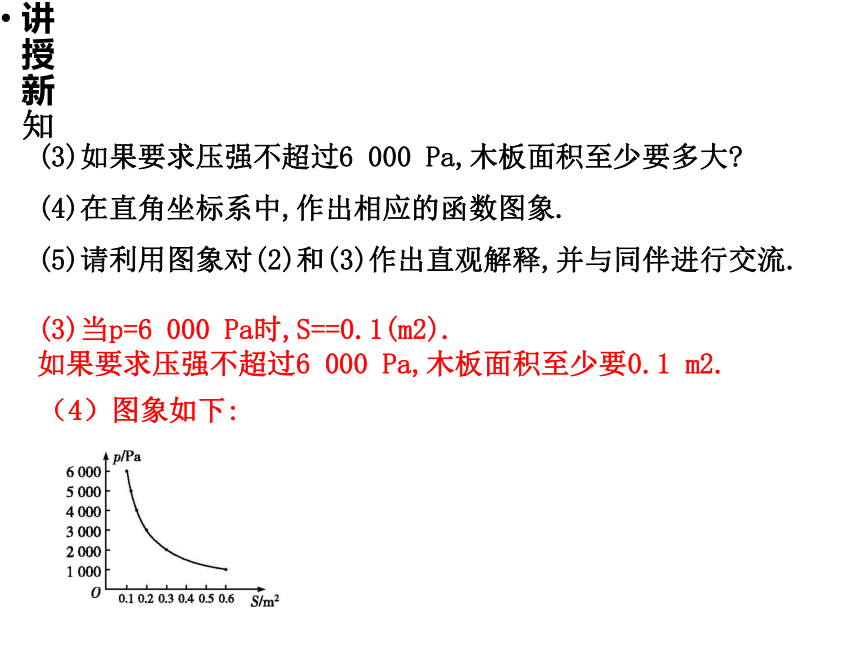
(3)如果要求压强不超过6 000 Pa,木板面积至少要多大
(4)在直角坐标系中,作出相应的函数图象.
(5)请利用图象对(2)和(3)作出直观解释,并与同伴进行交流.
(3)当p=6 000 Pa时,S==0.1(m2).
如果要求压强不超过6 000 Pa,木板面积至少要0.1 m2.
(4)图象如下:
范例应用
例1 蓄电池的电压为定值.使用此电源时,用电器的电流I(A)与电阻
R(Ω)之间的函数关系如图所示.
(1)蓄电池的电压是多少?你能写出这一函数的表达式吗?
(2)如果以此蓄电池为电源的用电器限制电流不得超过10 A,那么用
电器的可变电阻应控制在什么范围内?
解:(1)因为IR=U,把图象上的点A的坐标(9,4)代入,
得U=36.
函数的表达式为I=.
(2)当I=10 A时,解得R=3.6.所以当I≥10时,
可变电阻应不小于3.6 Ω.
讲授新课
知识点2 双曲线与直线的交点
如图,正比例函数=2x与反比例函数的图象交于A,B两点,点A的横坐标为2.求反比例函数的表达式及点B的坐标;
解:(1)当x=2时,由y=2x得y=4,
∵A(2,4),∴4=,即k=8,
∴,
∵正比例函数=2x与反比例函数的图象
交于A,B两点,
∴A、B关于原点对称,
∴B(﹣2,﹣4);
范例应用
例2 在平面直角坐标系xOy中,一次函数y=x+b的图象与x轴交于
A(2,0),与反比例函数的图象交于点B(3,n).
(1)求一次函数与反比例函数的表达式;
(2)若点P为x轴上的点,且△PAB的面积是2,求点P的坐标.
解:(1)∵一次函数y=x+b的图象与x轴交于点A(2,0),
∴2+b=0,∴b=﹣2,∴y=x﹣2,
当x=3时,y=1,
∴B(3,1),代入中,得到k=3,
∴反比例函数的解析式为y=.
(2)∵△PAB的面积是2,∴ PA 1=2,
∴PA=4,
∴P(﹣2,0)或(6,0).
当堂训练
叁
当堂训练
1.甲、乙两地相距s千米,汽车从甲地匀速行驶到乙地,
行驶的时间t(小时)关于行驶速度v(千米/时)的函数图象是( )
A. B.
C. D.
B
当堂训练
2.如果等腰三角形的面积为6,底边长为x,底边上的高为
y,则y与x的函数关系式为( )
A.y= B.y= C.y= D.y=
3.如果正比例函数图象与反比例函数图象的一个交点的
坐标为(3,﹣4),那么另一个交点的坐标为( )
A.(﹣3,﹣4) B.(3,4)
C.(﹣3,4) D.(﹣4,3)
A
C
当堂训练
4.车从甲地驶往乙地,行完全程所需的时间t(h)与
行驶的平均速度v(km/h)之间的反比例函数关系如图
所示.若列车要在2.5h内到达,则速度至少需要提高
到______km/h.
240
当堂训练
5.小明要把一篇文章录入电脑,完成录入的时间y(分)
与录入文字的速度x(字/分)之间的函数关系如图.
(1)求y与x之间的函数表达式;
(2)小明在19:20开始录入,要求完成录入时不超过
19:35,小明每分钟至少应录入多少个字?
解:(1)设y=,
把(150,10)代入得k=1500,
∴y与x的函数表达式为y=;
(2)∵当y=35﹣20=15时,x=100,
∵k>0,在第一象限内,y随x的增大而减小,
∴小明录入文字的速度至少为100字/分,
课堂小结
肆
课堂小结
1.反比例函数的图象与性质
2.反比例函数的应用
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学采取合理的方式,搜集整理与本节课有关的“好题”,被选中的同学下节课为全班展示。
谢
谢
第六章 反比例函数
3 反比例函数的应用
学习目标
学习目标
1.能根据实际问题中的条件确定反比例函数的表达式,会画出它的图象,能根据图象指出函数值随自变量的变化情况.
2.能通过探索实际问题列出函数表达式,利用反比例函数的性质解释实际问题,细心体会图象在解决问题时的作用.
3.通过对实际问题的分析与解决,让学生体验数学的价值,培养学生对数学的兴趣.
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
新课导入
1.什么是反比例函数
2.反比例函数的图象有什么性质
反比例函数:当k>0时,两支曲线分别在________象限,
在每一象限内,y的值随x的增大而______.
当k<0时,两支曲线分别在___________象限,
在每一象限内,y的值随x的增大而_____.
如果两个变量x、y之间的对应关系可以表示成y=
一、三
减小
二、四
增大
讲授新知
贰
讲授新知
知识点1 反比例函数的实际应用
某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为
了安全、迅速通过这片湿地,他们沿着前进路线铺垫了若干块木板,
构筑成一条临时通道,从而顺利完成了任务.你能解释他们这样做的
道理吗 当人和木板对湿地的压力一定时随着木板面积S(m2)的变化,
人和木板对地面的压强p(Pa)将如何变化 如果人和木板对湿地地面
的压力合计600 N,
(1)用含S的代数式表示p,p是S的反比例函数吗 为什么
(2)当木板面积为0.2 时,压强是多少
解:(1)p=,p是S的反比例函数.
(2)当S=0.2 时,p==3 000(Pa).
当木板面积为0.2 时,压强是3 000 Pa.
讲授新知
(3)如果要求压强不超过6 000 Pa,木板面积至少要多大
(4)在直角坐标系中,作出相应的函数图象.
(5)请利用图象对(2)和(3)作出直观解释,并与同伴进行交流.
(3)当p=6 000 Pa时,S==0.1(m2).
如果要求压强不超过6 000 Pa,木板面积至少要0.1 m2.
(4)图象如下:
范例应用
例1 蓄电池的电压为定值.使用此电源时,用电器的电流I(A)与电阻
R(Ω)之间的函数关系如图所示.
(1)蓄电池的电压是多少?你能写出这一函数的表达式吗?
(2)如果以此蓄电池为电源的用电器限制电流不得超过10 A,那么用
电器的可变电阻应控制在什么范围内?
解:(1)因为IR=U,把图象上的点A的坐标(9,4)代入,
得U=36.
函数的表达式为I=.
(2)当I=10 A时,解得R=3.6.所以当I≥10时,
可变电阻应不小于3.6 Ω.
讲授新课
知识点2 双曲线与直线的交点
如图,正比例函数=2x与反比例函数的图象交于A,B两点,点A的横坐标为2.求反比例函数的表达式及点B的坐标;
解:(1)当x=2时,由y=2x得y=4,
∵A(2,4),∴4=,即k=8,
∴,
∵正比例函数=2x与反比例函数的图象
交于A,B两点,
∴A、B关于原点对称,
∴B(﹣2,﹣4);
范例应用
例2 在平面直角坐标系xOy中,一次函数y=x+b的图象与x轴交于
A(2,0),与反比例函数的图象交于点B(3,n).
(1)求一次函数与反比例函数的表达式;
(2)若点P为x轴上的点,且△PAB的面积是2,求点P的坐标.
解:(1)∵一次函数y=x+b的图象与x轴交于点A(2,0),
∴2+b=0,∴b=﹣2,∴y=x﹣2,
当x=3时,y=1,
∴B(3,1),代入中,得到k=3,
∴反比例函数的解析式为y=.
(2)∵△PAB的面积是2,∴ PA 1=2,
∴PA=4,
∴P(﹣2,0)或(6,0).
当堂训练
叁
当堂训练
1.甲、乙两地相距s千米,汽车从甲地匀速行驶到乙地,
行驶的时间t(小时)关于行驶速度v(千米/时)的函数图象是( )
A. B.
C. D.
B
当堂训练
2.如果等腰三角形的面积为6,底边长为x,底边上的高为
y,则y与x的函数关系式为( )
A.y= B.y= C.y= D.y=
3.如果正比例函数图象与反比例函数图象的一个交点的
坐标为(3,﹣4),那么另一个交点的坐标为( )
A.(﹣3,﹣4) B.(3,4)
C.(﹣3,4) D.(﹣4,3)
A
C
当堂训练
4.车从甲地驶往乙地,行完全程所需的时间t(h)与
行驶的平均速度v(km/h)之间的反比例函数关系如图
所示.若列车要在2.5h内到达,则速度至少需要提高
到______km/h.
240
当堂训练
5.小明要把一篇文章录入电脑,完成录入的时间y(分)
与录入文字的速度x(字/分)之间的函数关系如图.
(1)求y与x之间的函数表达式;
(2)小明在19:20开始录入,要求完成录入时不超过
19:35,小明每分钟至少应录入多少个字?
解:(1)设y=,
把(150,10)代入得k=1500,
∴y与x的函数表达式为y=;
(2)∵当y=35﹣20=15时,x=100,
∵k>0,在第一象限内,y随x的增大而减小,
∴小明录入文字的速度至少为100字/分,
课堂小结
肆
课堂小结
1.反比例函数的图象与性质
2.反比例函数的应用
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学采取合理的方式,搜集整理与本节课有关的“好题”,被选中的同学下节课为全班展示。
谢
谢
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
