第十一章 三角形同步练习题(含解析)
文档属性
| 名称 | 第十一章 三角形同步练习题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 632.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
“三角形”综合测试题
(满分150分,时间120分钟)
一、选择题(每题4分,满分40分)
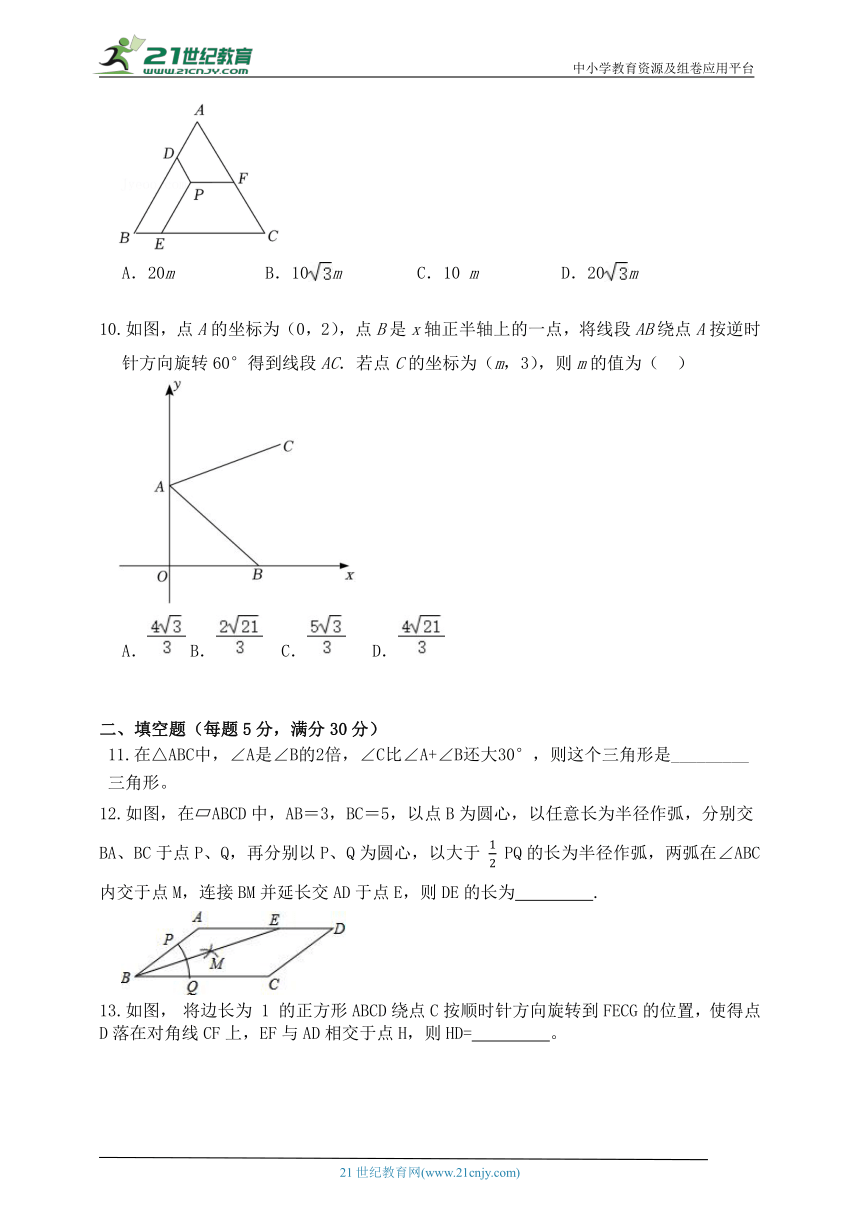
1.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A.315° B.270° C.180° D.135°
2.如图,△OAB绕点O逆时针旋转800到△OCD的位置,则∠ACO等于( )
A.55 B.50° C.40° D.35°
3.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
4.如图,在 中, , ,AD是斜边BC上的中线,将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于( )
A.120° B.108° C.72° D.36°
5.三角形两边的长是2和4,第三边的长是方程x2﹣12x+35=0的根,则该三角形的周长为( )
A.11 B.13 C.11或13 D.以上都不对
6.如图摆放的一副学生用直角三角板,∠F=30o,∠C=45o,AB与DE相交于点G,当EF//BC时,∠EGB的度数是( )
A.135° B.120° C.115° D.105°
7.如图,直线EF//GH,中,∠C=90o,顶点A在GH上,顶点B在EF上,且BA平分∠DBE,若∠CAD=26o,则∠BAD的度数为( )
A.26o B.32o C.34o D.45o
8.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1 B.+ C.2+1 D.2-
9.如图,等边三角形ABC是一块边长为20m的草坪,点P是草坪内的任意一点,过点P有三条小路PD,PE,PF,且满足PE∥AB,PF∥BC,PD∥AC,则三条小路的总长度为( )
A.20m B.10m C.10 m D.20m
10.如图,点A的坐标为(0,2),点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为(m,3),则m的值为( )
A. B. C. D.
二、填空题(每题5分,满分30分)
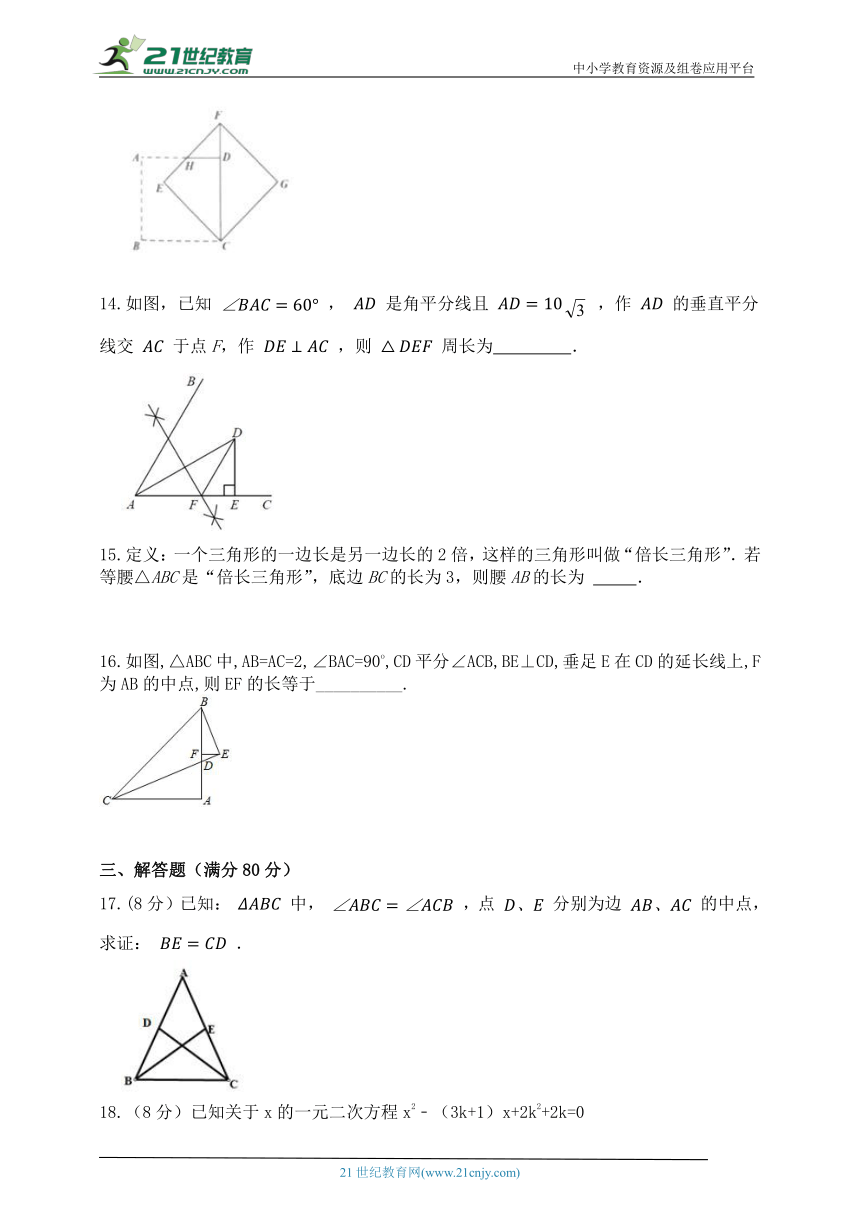
11.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大30°,则这个三角形是_________三角形。
12.如图,在 ABCD中,AB=3,BC=5,以点B为圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于 PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为 .
13.如图, 将边长为 1 的正方形ABCD绕点C按顺时针方向旋转到FECG的位置,使得点D落在对角线CF上,EF与AD相交于点H,则HD= 。
14.如图,已知 , 是角平分线且 ,作 的垂直平分线交 于点F,作 ,则 周长为 .
15.定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰△ABC是“倍长三角形”,底边BC的长为3,则腰AB的长为 .
16.如图,△ABC中,AB=AC=2,∠BAC=90o,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,F为AB的中点,则EF的长等于__________.
解答题(满分80分)
17.(8分)已知: 中, ,点 分别为边 的中点,求证: .
18.(8分)已知关于x的一元二次方程x2﹣(3k+1)x+2k2+2k=0
(1)求证:无论k取何实数值,方程总有实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c恰好是这个方程的两个根,求此三角形的三边长?
19.(8分)点P是∠AOB的内部任意一点,PM⊥OA,PN⊥OB,垂足分别是M、N,D是OP的中点(1)求证:DM=DN
(2)连接MN,当∠MPN=______时,△DMN是等边三角形;
(3)探索∠MPN与∠MDN的数量关系,并说明理由。
20.问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC,若∠BAE=90°,∠B=45°,则∠DAC= .
思考:
变式(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗 说明理由;
变式(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
21.如图,已知△AHB是等腰直角三角形.∠AHB=90°,△AHG,△BHC,△ABE是等边三角形,GH交AE于点F.CH交BE于点D.记四边形EFHD的面积为S1,△BCD的面积S2,求的值。
22.如图,△ABC是边长为6cm的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以2厘米/每秒的相同速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.设运动时间为t秒.
(1)用含t的式子表示:AP= ,AE= ,BE= ,
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生改变,请说明理由.
23.(原创)
如图,在正方形ABCD中,边长为4.
点E是边BC上的一点,连结AE.点F是线段CD上的点
①用尺规作图作出点F,使点F到AD、AE的距离相等。(保留作图痕迹,不写作法)
②当BE=3CE时,①若△AEF是直角三角形,求CF的长;
(2)点E是边CD上的一点,连结AE.点M是线段AE上的一个动点.
在线段AE上是否存在点G,使得∠BGC=90°,若存在,请探究BG、CG、DG之间的数量关系;若不存在,请说明理由.
参考答案
选择题
A
提示:∵∠C=900 ∴1800-∠1+1800-∠2=900,∴∠1+∠2=2700
B
提示:在 OAC中,OA=OC,∠AOC=800, ∴∠ACO==500
D
B
提示:∵在中,,,
∴.
∵AD是斜边BC上的中线,
∴,
∴,,
∴
∵将△ACD沿AD对折,使点C落在点F处,
∴,
∴.
A
提示:解方程x2﹣12x+35=0得x1=5,x2=7,当三角形的三边为2,4,7时,2+4=6<7,
不符合三角形的三边关系定理,不能组成三角形;当三角形的三边为2,4,5时,符合三角形的三边关系定理,能组成三角形,此时三角形的周长是2+4+5=11;综合上述:三角形的周长是11
D
提示:过点G作HG/\!/BC/\!/EF,则有∠HGB=∠B,∠HGE=∠E,∠F=30°,∠C=45°,可以得到∠E=60°,∠B=45°,有∠EGB=∠HGE+∠HGB
B
提示:∵∠C=90°,∠CAD=26°,
∴∠ADC=90°-26°=64°,
∴∠HDB=∠ADC=64°,
∵直线EF∥直线GH,
∴∠DBE=∠HDF=64°,
∵BA平分∠DBE,
∴∠ABE=∠AEB=32°,
∵直线EF∥直线GH,
∴∠BAD=∠ABE=32°
B
A
C
填空题
钝角三角形
提示:由题意可列方程组解出∠C=1050
12.2
提示:容易推证 ABE为等腰三角形,AB=AE=3,DE=5-3=2
13.-1
提示:∵四边形ABCD为边长为1的正方形,
∴CD=1,∠CDA=90 ,
∵边长为1的正方形ABCD绕点C按顺时针方向旋转到FECG的位置,使得点D落在对角线CF上,
∴CF=,∠CFE=45 ,
∴△DFH为等腰直角三角形,
∴DH=DF=CF CD= 1
14. 15+5
提示:AD=10,DE=5,AE=15, 周长为15+5
6
16.﹣1
提示:延长BE、CA交于点G,
∵AB=AC=2,∠BAC=90°,
∴由勾股定理可知:BC=2,
∵CD平分∠ACB,
∴∠BCE=∠ACE,
∵BE⊥CD,
∴∠BEC=∠CEG.
∴△BCG是等腰三角形,
∴BE=GE,CG=CB=2,
∵AC=2,
∴AG=CG﹣AC=2﹣2,
∵F是AB的中点,
∴BE=GE,
∴EF=AG=(2﹣2)=﹣1,
三、解答题
17.证明:∵∠ABC=∠ACB,
∴AB=AC,
∵点D. E分别是AB、AC的中点。
∴AD=AE,
在△ABE与△ACD中,
AD=AE,∠A=∠A,AC=AB
∴△ABE≌△ACD,
∴BE=CD.
18.(1)证明:∵△=b2﹣4ac=(3k+1)2﹣4(2k2+2k)=9k2+6k+1﹣8k2﹣8k=k2﹣2k+1=(k﹣1)2≥0
∴无论k取何值,方程总有实数根.
(2)解:①若a=6为底边,则b,c为腰长,则b=c,则△=0.
∴(k﹣1)2=0,解得:k=1.
此时原方程化为x2﹣4x+4=0,
∴x1=x2=2,即b=c=2.
此时△ABC三边为6,2,2不能构成三角形,故舍去;
②若a=b为腰,则b,c中一边为腰,不妨设b=a=6,
代入方程:62﹣6(3k+1)+2k2+2k=0,
解得k=3或5,
则原方程化为x2﹣10x+24=0或x2﹣16x+60=0,
解得x1=4,x2=6或x1=6,x2=10,
即b=6,c=4,或b=6,c=10,
此时△ABC三边为6,6,4或6,6,10能构成三角形,
周长为6+6+4=16或6+6+10=22.
18.(1)∵PM⊥OA,D是OP的中点,
∴MD=OD,
∵PN⊥OB,D是OP的中点,
∴ND=OD
∴ MD=ND
(2)当∠MPN=150°时,△DMN是等边三角形.理由如下:
∵∠MPN=150°,PM⊥OA,PN⊥OB,
∴∠MON=30°,
由(1)可知MD=OD,ND=OD,
∴∠MDP=2∠MOD,∠NDP=2∠NOD
∴∠MDN=2∠MON=60°,
∵MD=ND.
∴△DMN是等边三角形.
(3) 由(2)可知∠MDN=2∠MON,∠MPN+∠MON =180°
∴∠MPN=180°-∠MON=180°-∠MDN
∴∠MPN=180°-∠MDN.
19.解:(1)∵△ABC是边长为6cm的等边三角形,
∴∠A=60°,
根据题意得:AP=2tcm,
∵PE⊥AB,
∴AE=AP cos60°=t(cm),
∴BE=AB-AE=6-t(cm);
(2)∵∠C=60°,∠BQD=30°,
∴△PCQ是直角三角形,
∴PC=QC,
根据题意得:BQ=2tcm,则CQ=BC+BQ=6+2t(cm),PC=AC-AP=6-2t(cm),
∴6-2t=(6+2t),
解得:t=1,
∴AP=2;
(3)当点P、Q运动时,线段DE的长度不会改变.理由如下:
作QF⊥AB,交直线AB的延长线于点F,连接QE,PF,
又∵PE⊥AB于E,
∴∠DFQ=∠AEP=90°,
∵点P、Q速度相同,
∴AP=BQ,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠FBQ=60°,
在△APE和△BQF中,
∵∠AEP=∠BFQ=90°,
∴∠APE=∠BQF,
∴在△APE和△BQF中,
∠AEP=∠BFQ ∠A=∠FBQ AP=BQ
,∴△APE≌△BQF
∴AE=BF,PE=QF且PE∥QF,
∴四边形PEQF是平行四边形,
∴DE=EF,
∵EF=BE+BF=BE+AE=AB,
∴DE=AB,
又∵等边△ABC的边长为6,
∴DE=3,
∴当点P、Q运动时,线段DE的长度不会改变.
19.
(1)
①若∠AFE=90°,设CF=x,
在Rt ABE中,AB=8,BE=×8=6,AE=10,CE=8-6=2,
EF2=22+x2,AF2=(8-x)2+82
∴102=22+x2 +(8-x)2+82
∴x1=x2=4
若∠AEF=90°,设CF=x
由上可得:102+22+x2 =(8-x)2+82
X=
故CF的长为4或
存在。
∵DE=3CE,CD=4,∴DE=3,CE=1
∴AE=
以点B为坐标原点,以直线BC、BA分别为x轴和y轴,建立如图4所示的平面直角坐标系,则A(0,4)、B(0,0)、C(4,0)、D(4,4)、E(4,1)
易求得直线AE的解析式为y=x+4
设点M坐标为(m,m+4)(0≤m≤4)
则MB2=m2+(m+4)2=m2-6m+16
MC2=(m-4)2+(m+4)2=m2-14m+32
BC2=16
∵∠BMC=90°
∴MB2+MC2=BC2
∴m2-6m+16+m2-14m+32=16,∴25m2-160m+256=0,即(5m-16)2=0,∴m=
∴M(,)
于是BM2= , CM2= , DM2=
∴DM2=BM·CM ()
∴在线段AE上存在点M,使得∠BMC=90°,且DM2=BM·CM.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
“三角形”综合测试题
(满分150分,时间120分钟)
一、选择题(每题4分,满分40分)
1.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A.315° B.270° C.180° D.135°
2.如图,△OAB绕点O逆时针旋转800到△OCD的位置,则∠ACO等于( )
A.55 B.50° C.40° D.35°
3.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
4.如图,在 中, , ,AD是斜边BC上的中线,将△ACD沿AD对折,使点C落在点F处,线段DF与AB相交于点E,则∠BED等于( )
A.120° B.108° C.72° D.36°
5.三角形两边的长是2和4,第三边的长是方程x2﹣12x+35=0的根,则该三角形的周长为( )
A.11 B.13 C.11或13 D.以上都不对
6.如图摆放的一副学生用直角三角板,∠F=30o,∠C=45o,AB与DE相交于点G,当EF//BC时,∠EGB的度数是( )
A.135° B.120° C.115° D.105°
7.如图,直线EF//GH,中,∠C=90o,顶点A在GH上,顶点B在EF上,且BA平分∠DBE,若∠CAD=26o,则∠BAD的度数为( )
A.26o B.32o C.34o D.45o
8.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.+1 B.+ C.2+1 D.2-
9.如图,等边三角形ABC是一块边长为20m的草坪,点P是草坪内的任意一点,过点P有三条小路PD,PE,PF,且满足PE∥AB,PF∥BC,PD∥AC,则三条小路的总长度为( )
A.20m B.10m C.10 m D.20m
10.如图,点A的坐标为(0,2),点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为(m,3),则m的值为( )
A. B. C. D.
二、填空题(每题5分,满分30分)
11.在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大30°,则这个三角形是_________三角形。
12.如图,在 ABCD中,AB=3,BC=5,以点B为圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于 PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为 .
13.如图, 将边长为 1 的正方形ABCD绕点C按顺时针方向旋转到FECG的位置,使得点D落在对角线CF上,EF与AD相交于点H,则HD= 。
14.如图,已知 , 是角平分线且 ,作 的垂直平分线交 于点F,作 ,则 周长为 .
15.定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰△ABC是“倍长三角形”,底边BC的长为3,则腰AB的长为 .
16.如图,△ABC中,AB=AC=2,∠BAC=90o,CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,F为AB的中点,则EF的长等于__________.
解答题(满分80分)
17.(8分)已知: 中, ,点 分别为边 的中点,求证: .
18.(8分)已知关于x的一元二次方程x2﹣(3k+1)x+2k2+2k=0
(1)求证:无论k取何实数值,方程总有实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c恰好是这个方程的两个根,求此三角形的三边长?
19.(8分)点P是∠AOB的内部任意一点,PM⊥OA,PN⊥OB,垂足分别是M、N,D是OP的中点(1)求证:DM=DN
(2)连接MN,当∠MPN=______时,△DMN是等边三角形;
(3)探索∠MPN与∠MDN的数量关系,并说明理由。
20.问题:如图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC,若∠BAE=90°,∠B=45°,则∠DAC= .
思考:
变式(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗 说明理由;
变式(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.
21.如图,已知△AHB是等腰直角三角形.∠AHB=90°,△AHG,△BHC,△ABE是等边三角形,GH交AE于点F.CH交BE于点D.记四边形EFHD的面积为S1,△BCD的面积S2,求的值。
22.如图,△ABC是边长为6cm的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点,与点P同时以2厘米/每秒的相同速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.设运动时间为t秒.
(1)用含t的式子表示:AP= ,AE= ,BE= ,
(2)当∠BQD=30°时,求AP的长;
(3)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果发生改变,请说明理由.
23.(原创)
如图,在正方形ABCD中,边长为4.
点E是边BC上的一点,连结AE.点F是线段CD上的点
①用尺规作图作出点F,使点F到AD、AE的距离相等。(保留作图痕迹,不写作法)
②当BE=3CE时,①若△AEF是直角三角形,求CF的长;
(2)点E是边CD上的一点,连结AE.点M是线段AE上的一个动点.
在线段AE上是否存在点G,使得∠BGC=90°,若存在,请探究BG、CG、DG之间的数量关系;若不存在,请说明理由.
参考答案
选择题
A
提示:∵∠C=900 ∴1800-∠1+1800-∠2=900,∴∠1+∠2=2700
B
提示:在 OAC中,OA=OC,∠AOC=800, ∴∠ACO==500
D
B
提示:∵在中,,,
∴.
∵AD是斜边BC上的中线,
∴,
∴,,
∴
∵将△ACD沿AD对折,使点C落在点F处,
∴,
∴.
A
提示:解方程x2﹣12x+35=0得x1=5,x2=7,当三角形的三边为2,4,7时,2+4=6<7,
不符合三角形的三边关系定理,不能组成三角形;当三角形的三边为2,4,5时,符合三角形的三边关系定理,能组成三角形,此时三角形的周长是2+4+5=11;综合上述:三角形的周长是11
D
提示:过点G作HG/\!/BC/\!/EF,则有∠HGB=∠B,∠HGE=∠E,∠F=30°,∠C=45°,可以得到∠E=60°,∠B=45°,有∠EGB=∠HGE+∠HGB
B
提示:∵∠C=90°,∠CAD=26°,
∴∠ADC=90°-26°=64°,
∴∠HDB=∠ADC=64°,
∵直线EF∥直线GH,
∴∠DBE=∠HDF=64°,
∵BA平分∠DBE,
∴∠ABE=∠AEB=32°,
∵直线EF∥直线GH,
∴∠BAD=∠ABE=32°
B
A
C
填空题
钝角三角形
提示:由题意可列方程组解出∠C=1050
12.2
提示:容易推证 ABE为等腰三角形,AB=AE=3,DE=5-3=2
13.-1
提示:∵四边形ABCD为边长为1的正方形,
∴CD=1,∠CDA=90 ,
∵边长为1的正方形ABCD绕点C按顺时针方向旋转到FECG的位置,使得点D落在对角线CF上,
∴CF=,∠CFE=45 ,
∴△DFH为等腰直角三角形,
∴DH=DF=CF CD= 1
14. 15+5
提示:AD=10,DE=5,AE=15, 周长为15+5
6
16.﹣1
提示:延长BE、CA交于点G,
∵AB=AC=2,∠BAC=90°,
∴由勾股定理可知:BC=2,
∵CD平分∠ACB,
∴∠BCE=∠ACE,
∵BE⊥CD,
∴∠BEC=∠CEG.
∴△BCG是等腰三角形,
∴BE=GE,CG=CB=2,
∵AC=2,
∴AG=CG﹣AC=2﹣2,
∵F是AB的中点,
∴BE=GE,
∴EF=AG=(2﹣2)=﹣1,
三、解答题
17.证明:∵∠ABC=∠ACB,
∴AB=AC,
∵点D. E分别是AB、AC的中点。
∴AD=AE,
在△ABE与△ACD中,
AD=AE,∠A=∠A,AC=AB
∴△ABE≌△ACD,
∴BE=CD.
18.(1)证明:∵△=b2﹣4ac=(3k+1)2﹣4(2k2+2k)=9k2+6k+1﹣8k2﹣8k=k2﹣2k+1=(k﹣1)2≥0
∴无论k取何值,方程总有实数根.
(2)解:①若a=6为底边,则b,c为腰长,则b=c,则△=0.
∴(k﹣1)2=0,解得:k=1.
此时原方程化为x2﹣4x+4=0,
∴x1=x2=2,即b=c=2.
此时△ABC三边为6,2,2不能构成三角形,故舍去;
②若a=b为腰,则b,c中一边为腰,不妨设b=a=6,
代入方程:62﹣6(3k+1)+2k2+2k=0,
解得k=3或5,
则原方程化为x2﹣10x+24=0或x2﹣16x+60=0,
解得x1=4,x2=6或x1=6,x2=10,
即b=6,c=4,或b=6,c=10,
此时△ABC三边为6,6,4或6,6,10能构成三角形,
周长为6+6+4=16或6+6+10=22.
18.(1)∵PM⊥OA,D是OP的中点,
∴MD=OD,
∵PN⊥OB,D是OP的中点,
∴ND=OD
∴ MD=ND
(2)当∠MPN=150°时,△DMN是等边三角形.理由如下:
∵∠MPN=150°,PM⊥OA,PN⊥OB,
∴∠MON=30°,
由(1)可知MD=OD,ND=OD,
∴∠MDP=2∠MOD,∠NDP=2∠NOD
∴∠MDN=2∠MON=60°,
∵MD=ND.
∴△DMN是等边三角形.
(3) 由(2)可知∠MDN=2∠MON,∠MPN+∠MON =180°
∴∠MPN=180°-∠MON=180°-∠MDN
∴∠MPN=180°-∠MDN.
19.解:(1)∵△ABC是边长为6cm的等边三角形,
∴∠A=60°,
根据题意得:AP=2tcm,
∵PE⊥AB,
∴AE=AP cos60°=t(cm),
∴BE=AB-AE=6-t(cm);
(2)∵∠C=60°,∠BQD=30°,
∴△PCQ是直角三角形,
∴PC=QC,
根据题意得:BQ=2tcm,则CQ=BC+BQ=6+2t(cm),PC=AC-AP=6-2t(cm),
∴6-2t=(6+2t),
解得:t=1,
∴AP=2;
(3)当点P、Q运动时,线段DE的长度不会改变.理由如下:
作QF⊥AB,交直线AB的延长线于点F,连接QE,PF,
又∵PE⊥AB于E,
∴∠DFQ=∠AEP=90°,
∵点P、Q速度相同,
∴AP=BQ,
∵△ABC是等边三角形,
∴∠A=∠ABC=∠FBQ=60°,
在△APE和△BQF中,
∵∠AEP=∠BFQ=90°,
∴∠APE=∠BQF,
∴在△APE和△BQF中,
∠AEP=∠BFQ ∠A=∠FBQ AP=BQ
,∴△APE≌△BQF
∴AE=BF,PE=QF且PE∥QF,
∴四边形PEQF是平行四边形,
∴DE=EF,
∵EF=BE+BF=BE+AE=AB,
∴DE=AB,
又∵等边△ABC的边长为6,
∴DE=3,
∴当点P、Q运动时,线段DE的长度不会改变.
19.
(1)
①若∠AFE=90°,设CF=x,
在Rt ABE中,AB=8,BE=×8=6,AE=10,CE=8-6=2,
EF2=22+x2,AF2=(8-x)2+82
∴102=22+x2 +(8-x)2+82
∴x1=x2=4
若∠AEF=90°,设CF=x
由上可得:102+22+x2 =(8-x)2+82
X=
故CF的长为4或
存在。
∵DE=3CE,CD=4,∴DE=3,CE=1
∴AE=
以点B为坐标原点,以直线BC、BA分别为x轴和y轴,建立如图4所示的平面直角坐标系,则A(0,4)、B(0,0)、C(4,0)、D(4,4)、E(4,1)
易求得直线AE的解析式为y=x+4
设点M坐标为(m,m+4)(0≤m≤4)
则MB2=m2+(m+4)2=m2-6m+16
MC2=(m-4)2+(m+4)2=m2-14m+32
BC2=16
∵∠BMC=90°
∴MB2+MC2=BC2
∴m2-6m+16+m2-14m+32=16,∴25m2-160m+256=0,即(5m-16)2=0,∴m=
∴M(,)
于是BM2= , CM2= , DM2=
∴DM2=BM·CM ()
∴在线段AE上存在点M,使得∠BMC=90°,且DM2=BM·CM.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
