数学人教A版(2019)必修第二册8.3.1柱锥台体的表面积和体积(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.3.1柱锥台体的表面积和体积(共25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 13:51:48 | ||
图片预览




文档简介
(共25张PPT)
8.3.1 棱柱、棱柱、棱台的
表面积和体积
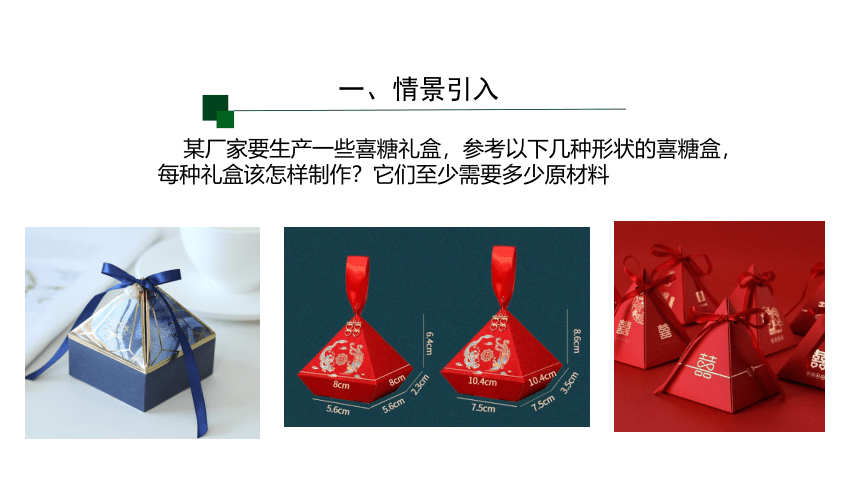
某厂家要生产一些喜糖礼盒,参考以下几种形状的喜糖盒,每种礼盒该怎样制作?它们至少需要多少原材料
一、情景引入
我们以四棱锥礼盒为例来简要说明制作过程
一、情景引入
问题1:将棱柱、棱锥、棱台的侧面展开,展开图是什么形状?怎样求棱柱、棱锥、棱台的表面积?
二、探索新知
二、探索新知
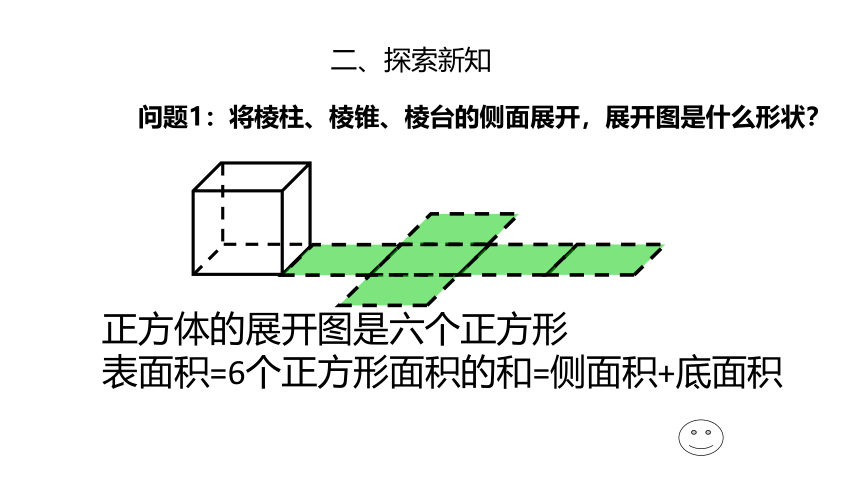
问题1:将棱柱、棱锥、棱台的侧面展开,展开图是什么形状?
正方体的展开图是六个正方形
表面积=6个正方形面积的和=侧面积+底面积
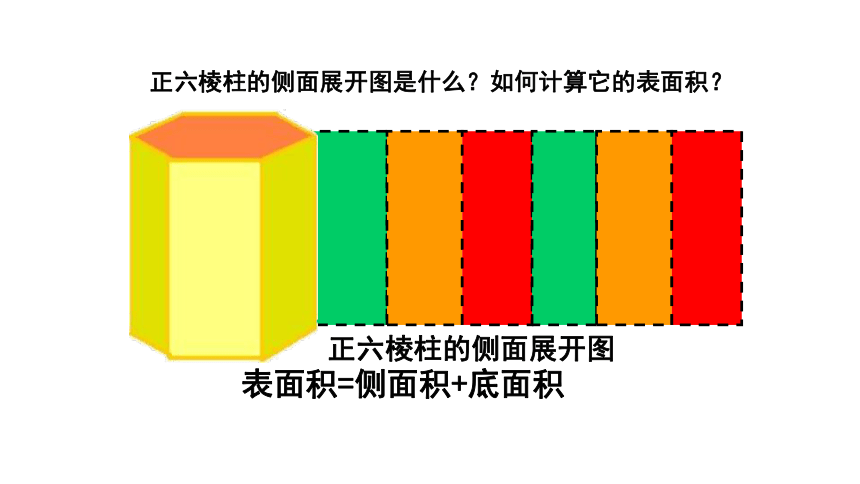
正六棱柱的侧面展开图是什么?如何计算它的表面积?
正六棱柱的侧面展开图
表面积=侧面积+底面积
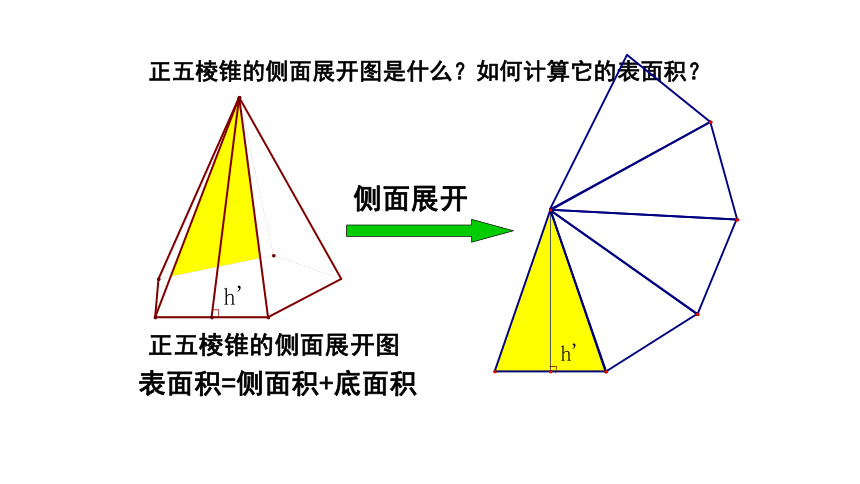
正五棱锥的侧面展开图是什么?如何计算它的表面积?
侧面展开
正五棱锥的侧面展开图
表面积=侧面积+底面积
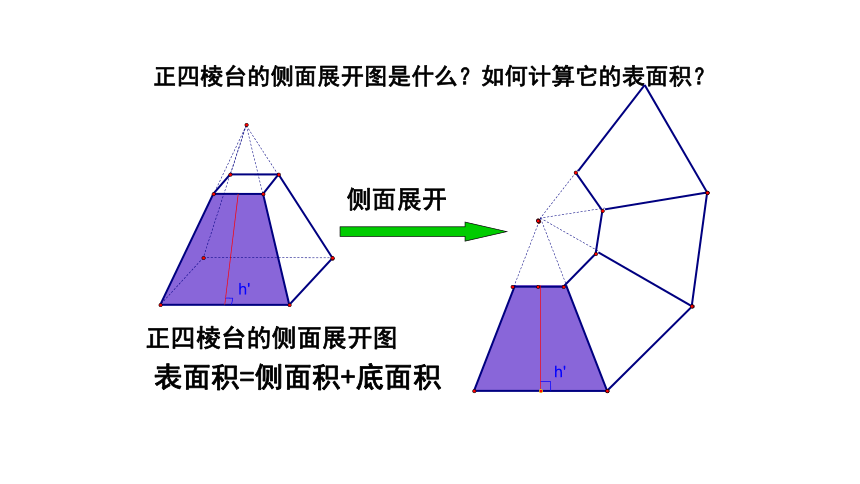
正四棱台的侧面展开图是什么?如何计算它的表面积?
侧面展开
h'
h'
正四棱台的侧面展开图
表面积=侧面积+底面积
二、探索新知
棱柱、棱锥、棱台的侧面展开,其侧面展开图分别是由若干个平行四边形、若干个三角形、若干个梯形组成的平面图形,侧面展开图的面积就是棱柱、棱锥、棱台的侧面积,棱柱、棱锥、棱台的表面积等于它们的侧面积与各自的底面积的和。
例1:如图,四面体P-ABC的各棱长均为a,求它的表面积.
回顾:四面体是三棱锥,各棱长相等的四面体是正四面体,是一种特殊的三棱锥。
例1:如图,四面体P-ABC的各棱长均为a,求它的表面积.
D
分析:四面体P-ABC的四个面是全等的正三角形,因此四面体的表面积等于其中任何一个面的面积的4倍.
∵PB=a,
∴四面体P-ABC的表面积为:
交BC于点D.
解:先求 的面积,过点P作
B
C
A
P
a
三、创设情景
消费扶贫是社会各界通过消费来自贫困地区和脱贫人口的产品与服务帮助脱贫群众增加收入的一种扶贫方式,浮山县也列为贫困地区,为了将浮山的农副产品(小米,红薯粉条,核桃...)推向大城市,需要设计漂亮的礼盒,你会设计什么样的礼盒? 你将如何制作?你设计的礼盒可以装多少浮山小米?应计算礼盒的什么量?
这是A同学设计的边长为30cm的正方体礼盒,你能算算最多可以装多少小米吗?
四、你是设计师
回忆:正方体体积公式V=
这是B同学设计的长宽高分别为15cm,25cm,30cm的长方体礼盒,你能算算最多可以装多少小米吗?
四、你是设计师
回忆:长方体体积公式V=
这是B同学设计的底面是十边形棱柱礼盒,你能算算最多可以装多少小米吗?
四、你是设计师
思考:柱体的体积该怎么计算?
祖晅原理祖顺是我国南北朝时期的数学家,是祖冲之的儿子。他提出:“幂势既同,则积不容异”。这句话的意思是:两个等高的体的体积相等。这一原理比欧洲早了1000多年。几何体若在所有等高处的水平截面的面积相等,则这两个几何祖冲之祖恒利用这个原理,巧妙的解决了柱体、椎体、球体的体积计算。
柱体的高是指两底面之 间的距离,即从一个底面上任意一点向另一个底面作垂线,这点与垂足之间的距离)
思考:柱体的体积该怎么计算?
柱体的高是指两底面之 间的距离,即从一个底面上任意一点向另一个底面作垂线,这点与垂足之间的距离.
一般地,如果棱柱的底面积是S,高是h,那么这个棱柱的体积
棱柱
思考:柱体与锥体体积之间有什么关系?
一个三棱柱可以分解成三个体积相等的三棱锥,如图所示:棱锥的体积等于同底等高的棱柱体积的三分之一
思考:锥体的体积该怎么计算?
锥体的高是指顶点到底面之 间的距离.
如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍。
( 是底面面积, 是高)
棱锥
棱台的体积
h1
h
S
S
,S为上、下底面面积,h 为台体高
思考:棱柱、棱锥、棱台的体积公式之间有什么关系?你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
上底扩大
上底缩小
V柱体=sh
例2 如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5 m,公共面ABCD是边长为1 m的正方形,那么这个漏斗的容积是多少立方米(精确到0.01 m3)?
五、实际问题
该几何体是由哪两个几何体拼接而成的?
每个几何体的体积如何计算?
例2 如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5 m,公共面ABCD是边长为1 m的正方形,那么这个漏斗的容积是多少立方米(精确到0.01 m3)?
解:由题意知
所以这个漏斗的容积
各面面积之和
展开图
棱柱、棱锥、棱台的表面积
棱锥
棱台
棱柱
棱柱、棱锥、
棱台的体积
课堂小结
8.3.1 棱柱、棱柱、棱台的
表面积和体积
某厂家要生产一些喜糖礼盒,参考以下几种形状的喜糖盒,每种礼盒该怎样制作?它们至少需要多少原材料
一、情景引入
我们以四棱锥礼盒为例来简要说明制作过程
一、情景引入
问题1:将棱柱、棱锥、棱台的侧面展开,展开图是什么形状?怎样求棱柱、棱锥、棱台的表面积?
二、探索新知
二、探索新知
问题1:将棱柱、棱锥、棱台的侧面展开,展开图是什么形状?
正方体的展开图是六个正方形
表面积=6个正方形面积的和=侧面积+底面积
正六棱柱的侧面展开图是什么?如何计算它的表面积?
正六棱柱的侧面展开图
表面积=侧面积+底面积
正五棱锥的侧面展开图是什么?如何计算它的表面积?
侧面展开
正五棱锥的侧面展开图
表面积=侧面积+底面积
正四棱台的侧面展开图是什么?如何计算它的表面积?
侧面展开
h'
h'
正四棱台的侧面展开图
表面积=侧面积+底面积
二、探索新知
棱柱、棱锥、棱台的侧面展开,其侧面展开图分别是由若干个平行四边形、若干个三角形、若干个梯形组成的平面图形,侧面展开图的面积就是棱柱、棱锥、棱台的侧面积,棱柱、棱锥、棱台的表面积等于它们的侧面积与各自的底面积的和。
例1:如图,四面体P-ABC的各棱长均为a,求它的表面积.
回顾:四面体是三棱锥,各棱长相等的四面体是正四面体,是一种特殊的三棱锥。
例1:如图,四面体P-ABC的各棱长均为a,求它的表面积.
D
分析:四面体P-ABC的四个面是全等的正三角形,因此四面体的表面积等于其中任何一个面的面积的4倍.
∵PB=a,
∴四面体P-ABC的表面积为:
交BC于点D.
解:先求 的面积,过点P作
B
C
A
P
a
三、创设情景
消费扶贫是社会各界通过消费来自贫困地区和脱贫人口的产品与服务帮助脱贫群众增加收入的一种扶贫方式,浮山县也列为贫困地区,为了将浮山的农副产品(小米,红薯粉条,核桃...)推向大城市,需要设计漂亮的礼盒,你会设计什么样的礼盒? 你将如何制作?你设计的礼盒可以装多少浮山小米?应计算礼盒的什么量?
这是A同学设计的边长为30cm的正方体礼盒,你能算算最多可以装多少小米吗?
四、你是设计师
回忆:正方体体积公式V=
这是B同学设计的长宽高分别为15cm,25cm,30cm的长方体礼盒,你能算算最多可以装多少小米吗?
四、你是设计师
回忆:长方体体积公式V=
这是B同学设计的底面是十边形棱柱礼盒,你能算算最多可以装多少小米吗?
四、你是设计师
思考:柱体的体积该怎么计算?
祖晅原理祖顺是我国南北朝时期的数学家,是祖冲之的儿子。他提出:“幂势既同,则积不容异”。这句话的意思是:两个等高的体的体积相等。这一原理比欧洲早了1000多年。几何体若在所有等高处的水平截面的面积相等,则这两个几何祖冲之祖恒利用这个原理,巧妙的解决了柱体、椎体、球体的体积计算。
柱体的高是指两底面之 间的距离,即从一个底面上任意一点向另一个底面作垂线,这点与垂足之间的距离)
思考:柱体的体积该怎么计算?
柱体的高是指两底面之 间的距离,即从一个底面上任意一点向另一个底面作垂线,这点与垂足之间的距离.
一般地,如果棱柱的底面积是S,高是h,那么这个棱柱的体积
棱柱
思考:柱体与锥体体积之间有什么关系?
一个三棱柱可以分解成三个体积相等的三棱锥,如图所示:棱锥的体积等于同底等高的棱柱体积的三分之一
思考:锥体的体积该怎么计算?
锥体的高是指顶点到底面之 间的距离.
如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积是棱锥的体积的3倍。
( 是底面面积, 是高)
棱锥
棱台的体积
h1
h
S
S
,S为上、下底面面积,h 为台体高
思考:棱柱、棱锥、棱台的体积公式之间有什么关系?你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗?
上底扩大
上底缩小
V柱体=sh
例2 如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5 m,公共面ABCD是边长为1 m的正方形,那么这个漏斗的容积是多少立方米(精确到0.01 m3)?
五、实际问题
该几何体是由哪两个几何体拼接而成的?
每个几何体的体积如何计算?
例2 如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5 m,公共面ABCD是边长为1 m的正方形,那么这个漏斗的容积是多少立方米(精确到0.01 m3)?
解:由题意知
所以这个漏斗的容积
各面面积之和
展开图
棱柱、棱锥、棱台的表面积
棱锥
棱台
棱柱
棱柱、棱锥、
棱台的体积
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
