人教版高中数学必修第二册8.1— 8.3同步测试 滚动训练(含解析)
文档属性
| 名称 | 人教版高中数学必修第二册8.1— 8.3同步测试 滚动训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 218.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 00:00:00 | ||
图片预览



文档简介
人教版高中数学必修第二册8.1——8.3同步测试滚动训练
(时间:45分钟 分值:100分)
一、选择题(本大题共8小题,每小题5分,共40分)
1.下列说法中正确的是 ( )
A.三棱柱的侧面展开图一定是平行四边形
B.水平放置的正方形的直观图有可能是梯形
C.一个几何体的正视图和侧视图都是矩形,则该几何体是长方体
D.用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分形成的几何体就是圆台
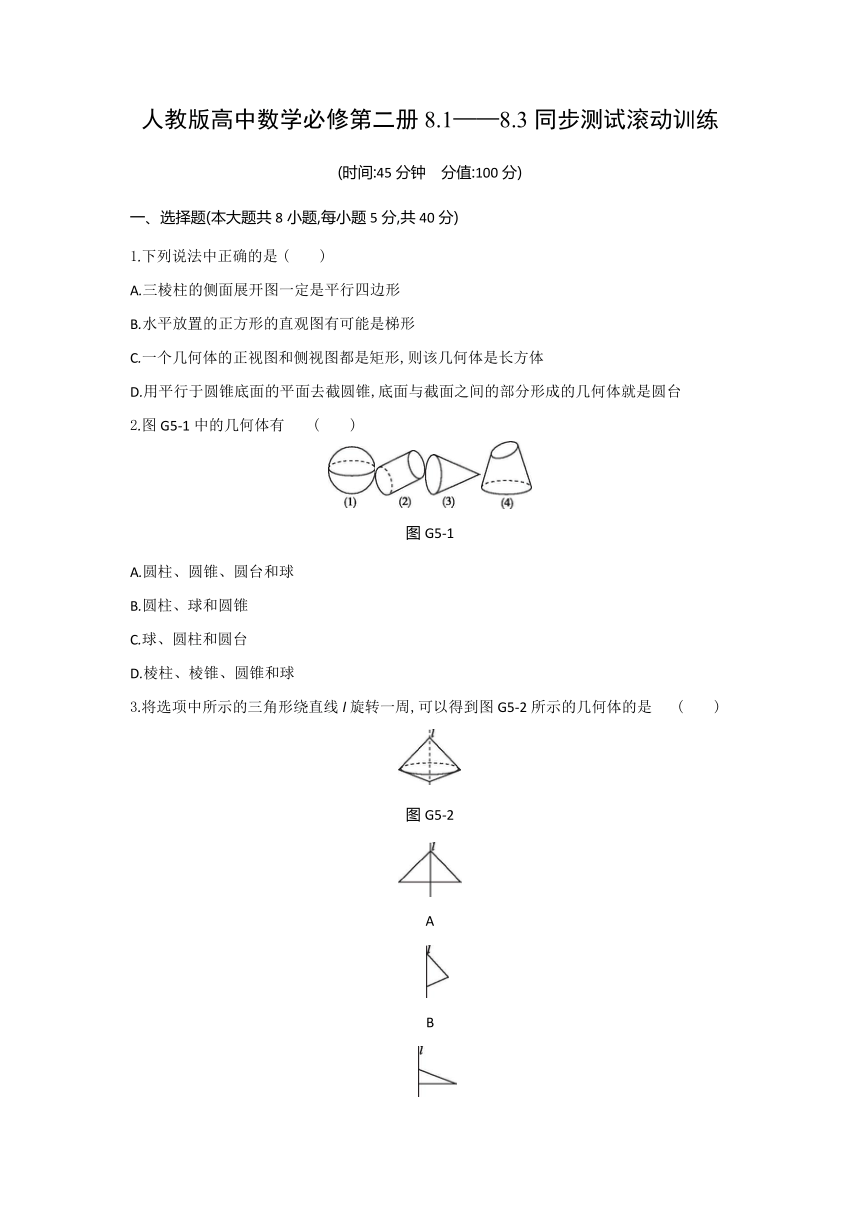
2.图G5-1中的几何体有 ( )
图G5-1
A.圆柱、圆锥、圆台和球
B.圆柱、球和圆锥
C.球、圆柱和圆台
D.棱柱、棱锥、圆锥和球
3.将选项中所示的三角形绕直线l旋转一周,可以得到图G5-2所示的几何体的是 ( )
图G5-2
A
B
C
D
图G5-3
4.在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为 ( )
A.1∶ B.1∶9
C.1∶3 D.1∶(3-1)
5.某柱体的正视图与侧视图是全等的正方形,俯视图是圆,记该柱体的表面积为S1,其内切球的表面积为S2,且S1=λS2,则λ= ( )
A.1 B.
C. D.
6.在如图G5-4所示的多面体ABCDB1C1D1中,四边形ABCD,四边形BCC1B1,四边形CDD1C1都是边长为6的正方形,则该多面体的体积为 ( )
图G5-4
A.72 B.144
C.180 D.216
7.将一个体积为36π的金属球切割加工成一个底面积为8π的圆柱,则当圆柱的体积最大时,其侧面积为 ( )
A.8π B.8π
C.6π D.9π
8.若圆锥的体积与球的体积相等,且圆锥的底面半径与球的直径相等,则圆锥的侧面积与球的表面积之比为 ( )
A.∶2 B.∶4
C.1∶2 D.∶4
二、填空题(本大题共4小题,每小题5分,共20分)
9.将一个等腰直角三角形绕其斜边所在直线旋转一周所得几何体的体积为V1,绕其一直角边所在直线旋转一周所得几何体的体积为V2,则= .
10.关于斜二测画法,有如下说法:
①在画直观图时,由于选轴的不同,所得的直观图可能不同;②等腰三角形的直观图仍然是等腰三角形;③梯形的直观图仍然是梯形;④正三角形的直观图一定为等腰三角形.
其中正确说法的序号是 .
11.在正四棱锥V-ABCD中,底面ABCD的面积为16,一条侧棱的长为2,则该棱锥的高为 .
12.设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2,若它们的侧面积相等,且=,则的值是 .
三、解答题(本大题共3小题,共40分)
13.(10分)如图G5-5,该几何体上半部分是母线长为5,底面半径为3的圆锥,下半部分是下底面半径为2,母线长为2的圆台,计算该几何体的表面积和体积.
图G5-5
14.(15分)已知一个圆锥的底面半径为2,母线长为4.
(1)求圆锥的侧面展开图的扇形的圆心角;
(2)若圆锥中内接一个高为的圆柱,求圆柱的表面积.
15.(15分)如图G5-6,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,且AB=BC=, A1A=2.
(1)求该直三棱柱的表面积;
(2)若把两个这样的直三棱柱拼成一个大棱柱,求大棱柱表面积的最小值.
图G5-6
参考答案与解析
1.D [解析] 对于选项A,三棱柱的每个侧面都是平行四边形,但是全部展开以后,那些平行四边形未必可以构成一个“大”平行四边形,故A错误.对于选项B,水平放置的正方形的直观图是平行四边形,不可能是梯形,故B错误.对于选项C,一个几何体的正视图和侧视图都是矩形,则该几何体不一定是长方体,也可能是圆柱,故C错误.对于选项D,根据圆台的定义可知D正确.故选D.
2.B [解析] 由图可知,(1)是球,(2)是圆柱,(3)是圆锥,(4)不是圆台,故选B.
3.B
4.D [解析] 由题意得,截得的小锥体与原来大锥体的体积之比为1∶3,故锥体被截面所分成的两部分的体积之比为1∶(3-1),故选D.
5.D [解析] 由已知可得,该柱体为底面直径与高相等的圆柱,设底面圆的半径为r,则高为2r,则S1=2πr2+2πr·(2r)=6πr2.易知该圆柱内切球的半径为r,则S2=4πr2, 则λ===,故选D.
6.C [解析] 如图,把该多面体补成正方体ABCD - A1B1C1D1,则该多面体的体积V=-=63-××63=180.故选C.
7.A [解析] 设球的半径为R,则由题意知πR3=36π,解得R=3.当圆柱的体积最大时,圆柱轴截面对角线的长等于球的直径.设圆柱的底面半径为r,则πr2=8π,解得r=2,所以圆柱的高h=2=2=2,所以圆柱的侧面积S=2πr·h=2π×2×2=8π,故选A.
8.A [解析] 设圆锥的底面半径为r,圆锥的高为h,则球的半径为,由题知πr2h=π·3,解得h=,∴圆锥的母线长为=r,∴圆锥的侧面积S1=×2πr×r=πr2,又球的表面积S2=4π2=πr2,∴=,故选A.
9. [解析] 设等腰直角三角形的斜边长为2,则直角边长为,则V1=,V2=,所以=.
10.①③ [解析] 由斜二测画法规则可知,正三角形、等腰三角形的直观图不一定是等腰三角形,故②④错误,易知①③正确.
11.6 [解析] 如图,取正方形ABCD的中心O,连接VO,AO,则VO就是正四棱锥V-ABCD的高.∵底面ABCD的面积为16,∴AO=2,又VA=2,∴VO===6,∴正四棱锥V-ABCD的高为6.
12. [解析] 由题意可得甲、乙两个圆柱的底面半径分别为r1=,r2=,甲、乙两个圆柱的高分别为h1=,h2=,因为它们的侧面积相等,所以2πr1h1=2πr2h2,即·=·,整理得==.
13.解:圆锥的侧面积S1=π×3×5=15π,圆台的侧面积S2=π×(3+2)×2=10π,
圆台的下底面面积S底=π×22=4π,
所以该几何体的表面积S=S1+S2+S底=15π+10π+4π=29π.
根据题意得,圆锥的高为4,圆台的高为,
则圆锥的体积V1=×π×32×4=12π,
圆台的体积V2=×π××(32+2×3+22)=π,
所以该几何体的体积V=V1+V2=12π+π.
14.解:(1)所求圆心角为==π.
(2)由题可知,圆锥的高为2,
因为圆柱的高为,所以圆柱的底面半径为1,
则圆柱的表面积S=2×π×12+2×π×1×=(2+2)π.
15.解:(1)该直三棱柱底面的面积为××=1,
侧面积为2×(++2)=4+4,故其表面积S=6+4.
(2)设两个这样的直三棱柱拼成一个大棱柱时重合的面的面积为S1,则大棱柱的表面积为2S-2S1,
所以当重合的面的面积最大时,大棱柱的表面积最小.
因为侧面AA1C1C的面积最大,
所以大棱柱表面积的最小值为2S-2=4+8.
(时间:45分钟 分值:100分)
一、选择题(本大题共8小题,每小题5分,共40分)
1.下列说法中正确的是 ( )
A.三棱柱的侧面展开图一定是平行四边形
B.水平放置的正方形的直观图有可能是梯形
C.一个几何体的正视图和侧视图都是矩形,则该几何体是长方体
D.用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分形成的几何体就是圆台
2.图G5-1中的几何体有 ( )
图G5-1
A.圆柱、圆锥、圆台和球
B.圆柱、球和圆锥
C.球、圆柱和圆台
D.棱柱、棱锥、圆锥和球
3.将选项中所示的三角形绕直线l旋转一周,可以得到图G5-2所示的几何体的是 ( )
图G5-2
A
B
C
D
图G5-3
4.在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为 ( )
A.1∶ B.1∶9
C.1∶3 D.1∶(3-1)
5.某柱体的正视图与侧视图是全等的正方形,俯视图是圆,记该柱体的表面积为S1,其内切球的表面积为S2,且S1=λS2,则λ= ( )
A.1 B.
C. D.
6.在如图G5-4所示的多面体ABCDB1C1D1中,四边形ABCD,四边形BCC1B1,四边形CDD1C1都是边长为6的正方形,则该多面体的体积为 ( )
图G5-4
A.72 B.144
C.180 D.216
7.将一个体积为36π的金属球切割加工成一个底面积为8π的圆柱,则当圆柱的体积最大时,其侧面积为 ( )
A.8π B.8π
C.6π D.9π
8.若圆锥的体积与球的体积相等,且圆锥的底面半径与球的直径相等,则圆锥的侧面积与球的表面积之比为 ( )
A.∶2 B.∶4
C.1∶2 D.∶4
二、填空题(本大题共4小题,每小题5分,共20分)
9.将一个等腰直角三角形绕其斜边所在直线旋转一周所得几何体的体积为V1,绕其一直角边所在直线旋转一周所得几何体的体积为V2,则= .
10.关于斜二测画法,有如下说法:
①在画直观图时,由于选轴的不同,所得的直观图可能不同;②等腰三角形的直观图仍然是等腰三角形;③梯形的直观图仍然是梯形;④正三角形的直观图一定为等腰三角形.
其中正确说法的序号是 .
11.在正四棱锥V-ABCD中,底面ABCD的面积为16,一条侧棱的长为2,则该棱锥的高为 .
12.设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2,若它们的侧面积相等,且=,则的值是 .
三、解答题(本大题共3小题,共40分)
13.(10分)如图G5-5,该几何体上半部分是母线长为5,底面半径为3的圆锥,下半部分是下底面半径为2,母线长为2的圆台,计算该几何体的表面积和体积.
图G5-5
14.(15分)已知一个圆锥的底面半径为2,母线长为4.
(1)求圆锥的侧面展开图的扇形的圆心角;
(2)若圆锥中内接一个高为的圆柱,求圆柱的表面积.
15.(15分)如图G5-6,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,且AB=BC=, A1A=2.
(1)求该直三棱柱的表面积;
(2)若把两个这样的直三棱柱拼成一个大棱柱,求大棱柱表面积的最小值.
图G5-6
参考答案与解析
1.D [解析] 对于选项A,三棱柱的每个侧面都是平行四边形,但是全部展开以后,那些平行四边形未必可以构成一个“大”平行四边形,故A错误.对于选项B,水平放置的正方形的直观图是平行四边形,不可能是梯形,故B错误.对于选项C,一个几何体的正视图和侧视图都是矩形,则该几何体不一定是长方体,也可能是圆柱,故C错误.对于选项D,根据圆台的定义可知D正确.故选D.
2.B [解析] 由图可知,(1)是球,(2)是圆柱,(3)是圆锥,(4)不是圆台,故选B.
3.B
4.D [解析] 由题意得,截得的小锥体与原来大锥体的体积之比为1∶3,故锥体被截面所分成的两部分的体积之比为1∶(3-1),故选D.
5.D [解析] 由已知可得,该柱体为底面直径与高相等的圆柱,设底面圆的半径为r,则高为2r,则S1=2πr2+2πr·(2r)=6πr2.易知该圆柱内切球的半径为r,则S2=4πr2, 则λ===,故选D.
6.C [解析] 如图,把该多面体补成正方体ABCD - A1B1C1D1,则该多面体的体积V=-=63-××63=180.故选C.
7.A [解析] 设球的半径为R,则由题意知πR3=36π,解得R=3.当圆柱的体积最大时,圆柱轴截面对角线的长等于球的直径.设圆柱的底面半径为r,则πr2=8π,解得r=2,所以圆柱的高h=2=2=2,所以圆柱的侧面积S=2πr·h=2π×2×2=8π,故选A.
8.A [解析] 设圆锥的底面半径为r,圆锥的高为h,则球的半径为,由题知πr2h=π·3,解得h=,∴圆锥的母线长为=r,∴圆锥的侧面积S1=×2πr×r=πr2,又球的表面积S2=4π2=πr2,∴=,故选A.
9. [解析] 设等腰直角三角形的斜边长为2,则直角边长为,则V1=,V2=,所以=.
10.①③ [解析] 由斜二测画法规则可知,正三角形、等腰三角形的直观图不一定是等腰三角形,故②④错误,易知①③正确.
11.6 [解析] 如图,取正方形ABCD的中心O,连接VO,AO,则VO就是正四棱锥V-ABCD的高.∵底面ABCD的面积为16,∴AO=2,又VA=2,∴VO===6,∴正四棱锥V-ABCD的高为6.
12. [解析] 由题意可得甲、乙两个圆柱的底面半径分别为r1=,r2=,甲、乙两个圆柱的高分别为h1=,h2=,因为它们的侧面积相等,所以2πr1h1=2πr2h2,即·=·,整理得==.
13.解:圆锥的侧面积S1=π×3×5=15π,圆台的侧面积S2=π×(3+2)×2=10π,
圆台的下底面面积S底=π×22=4π,
所以该几何体的表面积S=S1+S2+S底=15π+10π+4π=29π.
根据题意得,圆锥的高为4,圆台的高为,
则圆锥的体积V1=×π×32×4=12π,
圆台的体积V2=×π××(32+2×3+22)=π,
所以该几何体的体积V=V1+V2=12π+π.
14.解:(1)所求圆心角为==π.
(2)由题可知,圆锥的高为2,
因为圆柱的高为,所以圆柱的底面半径为1,
则圆柱的表面积S=2×π×12+2×π×1×=(2+2)π.
15.解:(1)该直三棱柱底面的面积为××=1,
侧面积为2×(++2)=4+4,故其表面积S=6+4.
(2)设两个这样的直三棱柱拼成一个大棱柱时重合的面的面积为S1,则大棱柱的表面积为2S-2S1,
所以当重合的面的面积最大时,大棱柱的表面积最小.
因为侧面AA1C1C的面积最大,
所以大棱柱表面积的最小值为2S-2=4+8.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
