2023-2024学年苏科版八年级数学上册第1—3章阶段性综合练习题(含解析)
文档属性
| 名称 | 2023-2024学年苏科版八年级数学上册第1—3章阶段性综合练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 295.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-07 00:00:00 | ||
图片预览

文档简介
2023-2024学年苏科版八年级数学上册《第1—3章》阶段性综合练习题(附答案)
一.选择题(共8小题,满分24分)
1.下列手机中的图标是轴对称图形的是( )
A. B.
C. D.
2.如图,由两个直角三角形和三个大正方形组成的图形,其中阴影部分面积是( )
A.16 B.25 C.144 D.169
3.下列能断定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=2∠B=70°
C.∠A=40°,∠B=70° D.AB=3,BC=6,周长为14
4.如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,则BC的长为( )
A.7cm B.10cm C.12cm D.22cm
5.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.a:b:c=5:12:13
C.a2=b2﹣c2 D.∠A=∠C﹣∠B
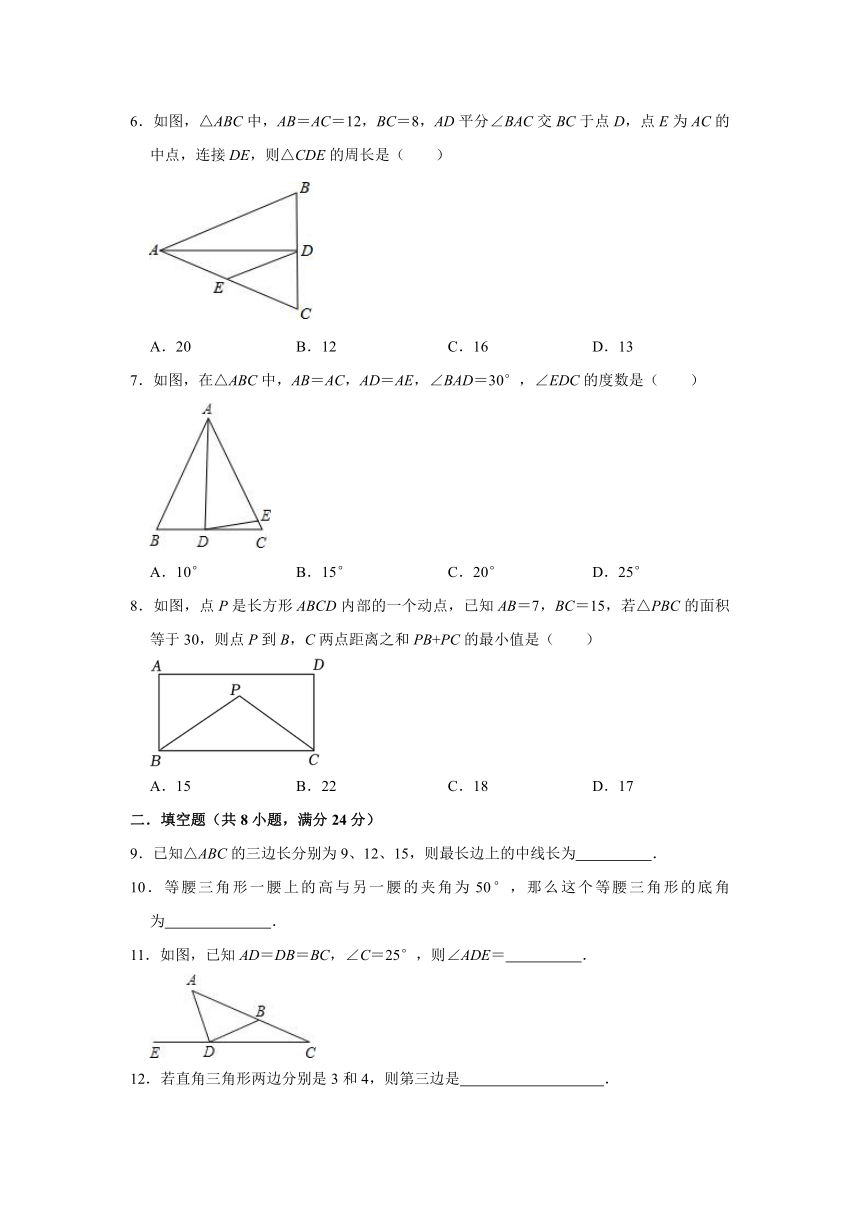
6.如图,△ABC中,AB=AC=12,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长是( )
A.20 B.12 C.16 D.13
7.如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠EDC的度数是( )
A.10° B.15° C.20° D.25°
8.如图,点P是长方形ABCD内部的一个动点,已知AB=7,BC=15,若△PBC的面积等于30,则点P到B,C两点距离之和PB+PC的最小值是( )
A.15 B.22 C.18 D.17
二.填空题(共8小题,满分24分)
9.已知△ABC的三边长分别为9、12、15,则最长边上的中线长为 .
10.等腰三角形一腰上的高与另一腰的夹角为50°,那么这个等腰三角形的底角为 .
11.如图,已知AD=DB=BC,∠C=25°,则∠ADE= .
12.若直角三角形两边分别是3和4,则第三边是 .
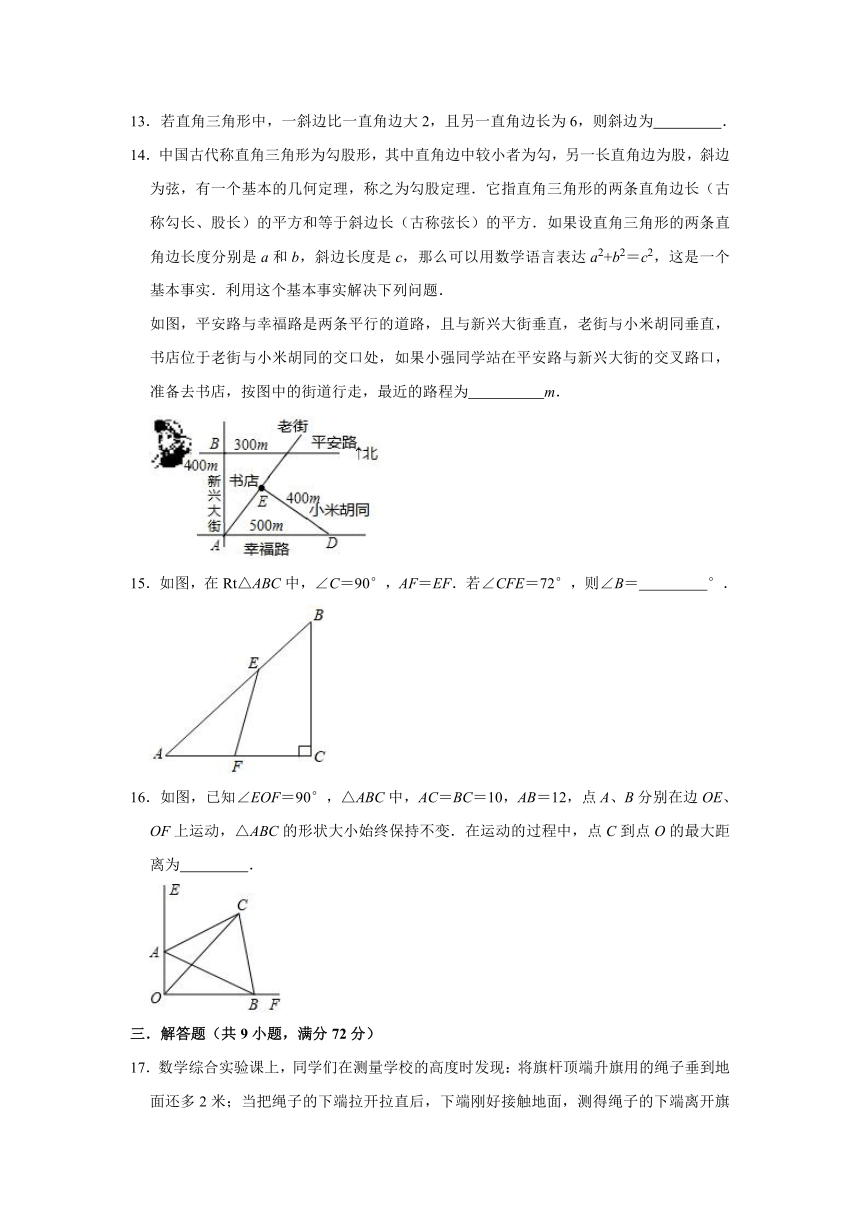
13.若直角三角形中,一斜边比一直角边大2,且另一直角边长为6,则斜边为 .
14.中国古代称直角三角形为勾股形,其中直角边中较小者为勾,另一长直角边为股,斜边为弦,有一个基本的几何定理,称之为勾股定理.它指直角三角形的两条直角边长(古称勾长、股长)的平方和等于斜边长(古称弦长)的平方.如果设直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么可以用数学语言表达a2+b2=c2,这是一个基本事实.利用这个基本事实解决下列问题.
如图,平安路与幸福路是两条平行的道路,且与新兴大街垂直,老街与小米胡同垂直,书店位于老街与小米胡同的交口处,如果小强同学站在平安路与新兴大街的交叉路口,准备去书店,按图中的街道行走,最近的路程为 m.
15.如图,在Rt△ABC中,∠C=90°,AF=EF.若∠CFE=72°,则∠B= °.
16.如图,已知∠EOF=90°,△ABC中,AC=BC=10,AB=12,点A、B分别在边OE、OF上运动,△ABC的形状大小始终保持不变.在运动的过程中,点C到点O的最大距离为 .
三.解答题(共9小题,满分72分)
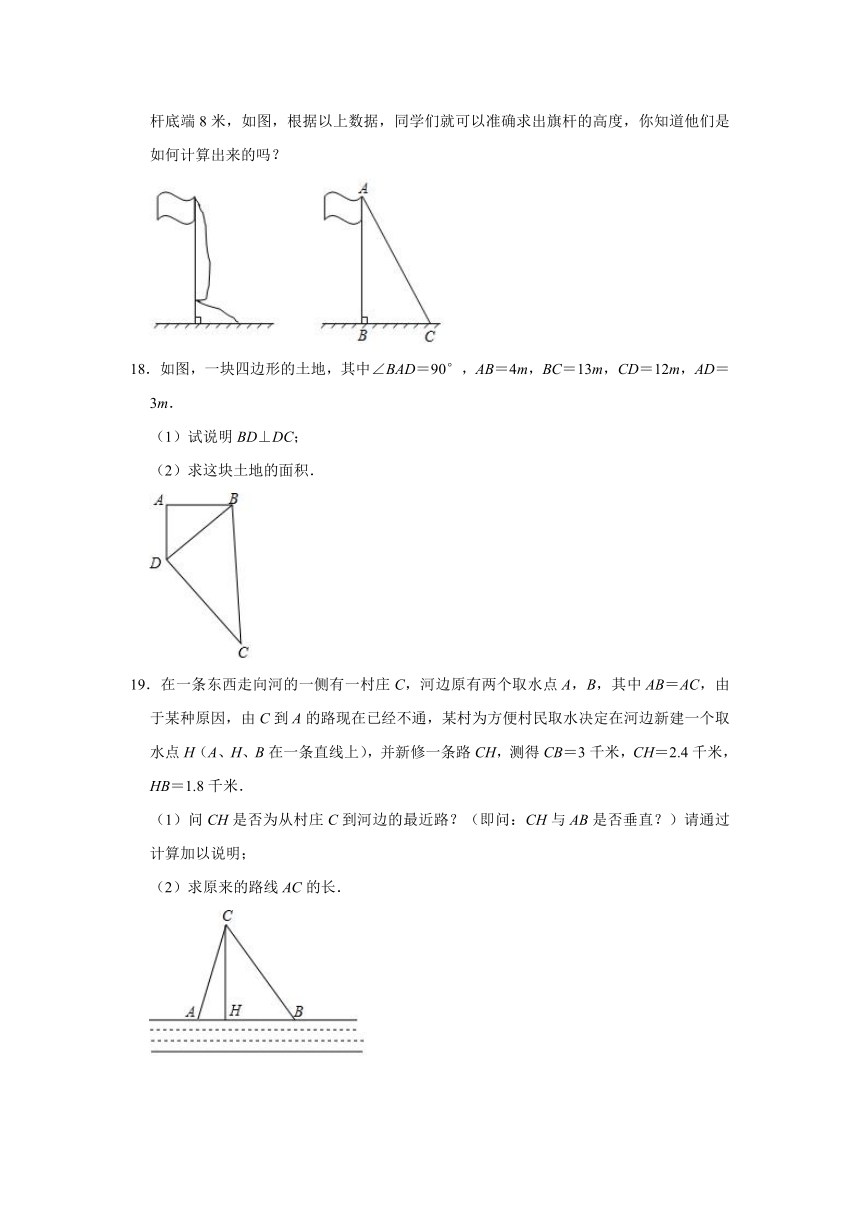
17.数学综合实验课上,同学们在测量学校的高度时发现:将旗杆顶端升旗用的绳子垂到地面还多2米;当把绳子的下端拉开拉直后,下端刚好接触地面,测得绳子的下端离开旗杆底端8米,如图,根据以上数据,同学们就可以准确求出旗杆的高度,你知道他们是如何计算出来的吗?
18.如图,一块四边形的土地,其中∠BAD=90°,AB=4m,BC=13m,CD=12m,AD=3m.
(1)试说明BD⊥DC;
(2)求这块土地的面积.
19.在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.
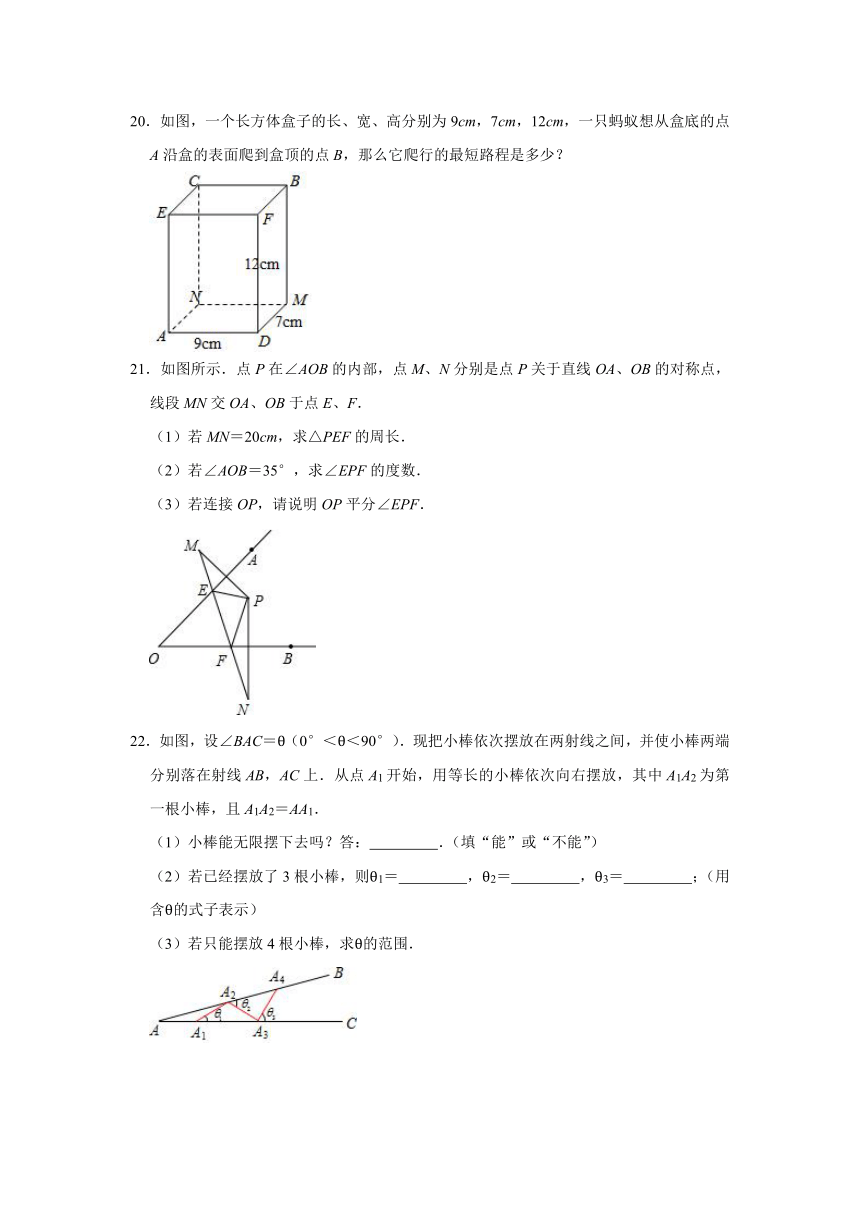
20.如图,一个长方体盒子的长、宽、高分别为9cm,7cm,12cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,那么它爬行的最短路程是多少?
21.如图所示.点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F.
(1)若MN=20cm,求△PEF的周长.
(2)若∠AOB=35°,求∠EPF的度数.
(3)若连接OP,请说明OP平分∠EPF.
22.如图,设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第一根小棒,且A1A2=AA1.
(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)
(2)若已经摆放了3根小棒,则θ1= ,θ2= ,θ3= ;(用含θ的式子表示)
(3)若只能摆放4根小棒,求θ的范围.
23.如图,△ABC中,BE⊥AC,CF⊥AB,垂足分别为E、F,M为BC的中点.
(1)求证:ME=MF.
(2)若∠A=50°,求∠FME的度数.
24.阅读下列材料:在四边形ABCD中,我们把一组邻边相等,剩下另一组邻边也相等的四边形称为筝形,如四边形ABCD中,若两邻边AB=AD,CB=CD,则把这样的四边形称之为筝形.
(1)如图1,在四边形ABCD中,AC同时平分∠BAD和∠BCD.求证:四边形ABCD是筝形.
(2)写出一条关于筝形对角线的性质 ,并利用图1证明此性质.
(3)如图2,在筝形ABCD中,AB=AD=26,BC=DC=25,AC=17,则筝形ABCD的面积为 .
25.(1)阅读理解:如图1,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,求∠APB的大小.
思路点拨:考虑到PA,PB,PC不在一个三角形中,采用转化与化归的数学思想,可以将△ABP绕顶点A逆时针旋转60°到△ACP'处,此时△ACP'≌△ABP,这样,就可以利用全等三角形知识,结合已知条件,将三条线段的长度转化到一个三角形中,从而求出∠APB的度数.请你写出完整的解答过程.
(2)变式拓展:请你利用第(1)问的解答思想方法,解答下面问题:
如图2,在△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,BE=8,CF=6,求EF的大小.
(3)能力提升:如图3,在Rt△ABC中,∠ACB=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,请直接写出(OA+OB+OC)2= .
参考答案
一.选择题(共8小题,满分24分)
1.解:A.不是轴对称图形,故此选项不合题意;
B.不是轴对称图形,故此选项不合题意;
C.是轴对称图形,故此选项符合题意;
D.不是轴对称图形,故此选项不合题意.
故选:C.
2.解:
根据勾股定理得出:AB=,
∴EF=AB=5,
∴阴影部分面积是25,
故选:B.
3.解:A、∠C=180°﹣40°﹣50°=90°,没有相等的角,则不是等腰三角形,本选项错误;
B、∵∠A=2∠B=70°,
∴∠B=35°,
∴∠C=75°,没有相等的角,则不是等腰三角形,本选项错误;
C、∠C=180°﹣40°﹣70°=70°,有相等的角,则是等腰三角形,本选项正确;
D、∵AB=3,BC=6,周长为14,
∴AC=14﹣6﹣3=5,没有相等的边,则不是等腰三角形,本选项错误;
故选:C.
4.解:根据折叠可得:AD=BD,
∵△ADC的周长为17cm,AC=5cm,
∴AD+DC=17﹣5=12(cm),
∵AD=BD,
∴BD+CD=12cm.
即BC=12cm,
故选:C.
5.解:A、∵∠A:∠B:∠C=3:4:5,且∠A+∠B+∠C=180°,可求得∠C≠90°,故△ABC不是直角三角形;
B、不妨设a=5,b=12,c=13,此时a2+b2=132=c2,即a2+b2=c2,故△ABC是直角三角形;
C、由条件可得到a2+c2=b2,满足勾股定理的逆定理,故△ABC是直角三角形;
D、由条件∠A=∠C﹣∠B,且∠A+∠B+∠C=180°,可求得∠C=90°,故△ABC是直角三角形;
故选:A.
6.解:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,CD=BC=4,
∵AD⊥BC,点E为AC的中点,
∴DE=EC=AC=6,
∴△CDE的周长=CD+DE+EC=16,
故选:C.
7.解:设∠EDC=x,∠B=∠C=y,
∠AED=∠EDC+∠C=x+y,
又因为AD=AE,所以∠ADE=∠AED=x+y,
则∠ADC=∠ADE+∠EDC=2x+y,
又因为∠ADC=∠B+∠BAD,
所以 2x+y=y+30,
解得x=15,
所以∠EDC的度数是15°.
故选:B.
8.解:设△BPC中BC边上的高是h,
∵S△PBC=30,BC=15,
∴BC h=30,
∴h=4,
∴动点P在与CB平行且与CB的距离是4的直线l上,
过点B作直线l的对称点B′,连接B′C交直线l于点P,B′C的长就是所求的最短距离之和PB+PC的最小值,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵BC=15,B′B=8,
∴B′C==17,
故选:D.
二.填空题(共8小题,满分24分)
9.解:∵92+122=225=152,
∴△ABC是直角三角形,
∴最长边上的中线长=×15=7.5.
故答案为:7.5.
10.解:①如图一,
∵△ABC是等腰三角形,BD⊥AC,∠ADB=90°,∠ABD=50°,
∴在直角△ABD中,∠A=90°﹣50°=40°,
∴∠C=∠ABC==70°;
②如图二,
∵△ABC是等腰三角形,BD⊥AC,∠ADB=90°,∠ABD=50°,
∴在直角△ABD中,∠BAD=90°﹣50°=40°,
又∵∠BAD=∠ABC+∠C,∠ABC=∠C,
∴∠C=∠ABC===20°.
故答案为:70°或20°.
11.解:∵DB=BC,∠C=25°,
∴∠BDC=∠C=25°,
∴∠ABD=∠BDC+∠C=50°,
∵AD=DB,
∴∠A=∠ABD=50°,
∴∠ADE=∠A+∠C=50°+25°=75°.
故答案为:75°.
12.解:设第三边为x,
(1)若4是直角边,则第三边x是斜边,由勾股定理得:
32+42=x2,
∴x=5;
(2)若4是斜边,则第三边x为直角边,由勾股定理得:
32+x2=42,
∴x=;
∴第三边的长为5或.
故答案为:5或.
13.解:设一条直角边为a,则斜边为a+2,
∵另一直角边长为6,
∴(a+2)2=a2+62,解得a=8,
∴a+2=8+2=10.
故答案为:10.
14.解:如图所示,设老街与平安路的交点为C,
∵BC∥AD,
∴∠ACB=∠DAE,
∵BC⊥AB,DE⊥AC,
∴∠CBA=∠AED=90°,
在△ABC和△DEA中,
,
∴△ABC≌△DEA(AAS),
∴AE=BC=300 m,
在Rt△ABC中,AC===500(m),
∴CE=AC﹣AE=500﹣300=200(m),
从B到E有两种走法:
①BA+AE=400+300=700(m);
②BC+CE=300+200=500(m),
∴最近的路程是500 m,
故答案为:500.
15.解:∵AF=EF,
∴∠A=∠AEF,
∵∠A+∠AEF=∠CFE=72°,
∴∠A=×72°=36°,
在Rt△ABC中,∠A=36°,
∴∠B=90°﹣36°=54°.
故答案为:54.
16.解:作CD⊥AB于D,连接OD,如图,
∵CA=CB,CD⊥AB,
∴AD=BD=AB=6,
在Rt△ACD中,CD==8,
∵∠AOB=90°,
∴OD=AB=6,
∵OC≤OD+DC(当且仅当C、D、O共线时取等号),
∴OC的最大值为OD+OC=6+8=14,
即点C到点O的最大距离为14.
故答案为14.
三.解答题(共9小题,满分72分)
17.解:设旗杆高x米,则绳子长为(x+2)米,
∵旗杆垂直于地面,
∴旗杆,绳子与地面构成直角三角形,
在Rt△ABC中,AB2+BC2=AC2,
∴x2+82=(x+2)2,
解方程,得x=15,
答:旗杆的高度为15米.
18.解:(1)在Rt△ABD中,∠BAD=90°,AB=4m,AD=3m,由勾股定理得:BD=5m,
∵BC=13m,CD=12m,BD=5m,
∴BD2+DC2=BC2,
∴∠BDC=90°,
即BD⊥DC;
(2)四边形ABCD的面积是S△ABD+S△BDC==36(m2).
19.解:(1)是,
理由是:在△CHB中,
∵CH2+BH2=(2.4)2+(1.8)2=9
BC2=9
∴CH2+BH2=BC2
∴CH⊥AB,
所以CH是从村庄C到河边的最近路
(2)设AC=x
在Rt△ACH中,由已知得AC=x,AH=x﹣1.8,CH=2.4
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣1.8)2+(2.4)2
解这个方程,得x=2.5,
答:原来的路线AC的长为2.5千米.
20.解:①如图1,展开后连接AB,则AB就是在表面上A到B的最短距离,
在Rt△ABM中,由勾股定理得:AB==20(cm);
②如图2,展开后连接AB,则AB就是在表面上A到B的最短距离,
在Rt△ADB中,由勾股定理得:AB==(cm);
③如图3,展开后连接AB,则AB就是在表面上A到B的最短距离,
在Rt△ANB中,由勾股定理得:AB==7(cm).
∴蚂蚁爬行的最短路程是20cm.
21.解:(1)∵点M、N分别是点P关于OA、OB的对称点,
∴ME=PE,NF=PF,MN=20cm,
∴ME+EF+NF=PE+EF+PF=MN=20cm,即△PEF的周长是20cm;
(2)如图,
∵点M、N分别是点P关于直线0A、OB的对称点,
∴OA垂直平分PM,OB垂直平分PN,
∴∠PRE=∠PTF=90°,
∴在四边形OTPR中,
∴∠MPN+∠AOB=180°,
∵∠EPF+2∠M+2∠N=180°,
即∠MPN+∠M+∠N=180°,
∴∠M+∠N=∠AOB=35°,
∴∠EPF=180°﹣35°×2=110°;
(3)如图,连接OM,ON,OP.
∵P,M关于OA对称,
∴OA垂直平分线段PM,
∴OM=OP,EM=EP,
∴∠OPM=∠OMP,∠EPM=∠EMP,
∴∠OPE=∠OME,
同法可证∠OPF=∠ONF,
∵OM=ON,
∴∠OME=∠ONF,
∴∠OPE=∠OPF,
∴OP平分∠EPF.
22.解:(1)小棒不能无限摆下去;
(2)∵小木棒长度都相等,
∴∠BAC=∠AA2A1,∠A2A1A3=∠A2A3A1,∠A3A2A4=∠A3A4A2,
由三角形外角性质,θ1=2θ,θ2=3θ,θ3=4θ;
(3)∵只能摆放4根小木棒,
∴,
解得18°≤θ<22.5°.
故答案为:不能;2θ,3θ,4θ.
23.(1)证明:∵BE⊥AC,CF⊥AB,
∴△BEC为直角三角形,∠BEC=90°,△CFB为直角三角形,∠CFB=90°,
∵M为BC中点,
∴FM=BC,EM=BC,
∴ME=MF;
(2)解:∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵MF=MB,ME=MC,
∴∠MFB=∠ABC,∠MEC=∠ACB,
∴∠BMF+∠CME=360°﹣2×130°=100°,
∴∠FME=180°﹣100°=80°.
24.(1)证明:如图1,∵AC同时平分∠BAD和∠BCD,
∴∠BAC=∠DAC,∠BCA=∠DCA,
∵AC=AC,
∴△BAC≌△DAC(ASA),
∴AB=AD、CB=CD,
∴四边形ABCD是筝形.
(2)筝形有一条对角线垂直平分另一条对角线,
证明:如图1,连接BD,
∵AB=AD,CB=CD,
∴点A、点C都在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC垂直平分BD,
∴筝形有一条对角线垂直平分另一条对角线.
(3)如图2,连接AC交BD于点O,设AO=x,
∵四边形ABCD是筝形,AB=AD=26,BC=DC=25,AC=17,
∴AC垂直线平分BD,CO=17﹣x,
∴∠AOB=∠COB=90°,BO=DO,
∴AB2﹣AO2=BC2﹣CO2=BO2,
∴262﹣x2=252﹣(17﹣x)2,
解得x=10,
∴AO=10,CO=17﹣10=7,
∴BO=DO===24,
∴BD=BO+DO=24+24=48,
∵AO⊥BD,CO⊥BD,
∴S筝形ABCD=BD AO+BD CO=×48×10+×48×7=408,
故答案为:408.
25.解:(1)∵将△ABP绕顶点A逆时针旋转60°到△ACP',
∴△ACP′≌△ABP,
∴AP′=AP=3、CP′=BP=4、∠AP′C=∠APB,
由题意知旋转角∠PAP′=60°,
∴△APP′为等边三角形,
PP′=AP=3,∠AP′P=60°,
易证△PP′C为直角三角形,且∠PP′C=90°,
∴∠APB=∠AP′C=∠AP′P+∠PP′C=60°+90°=150°;
(2)如图2,把△ABE绕点A逆时针旋转90°得到△ACE′,
由旋转的性质得,AE′=AE,CE′=BE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,
∵∠EAF=45°,
∴∠E′AF=∠CAE′+∠CAF=∠BAE+∠CAF=∠BAC﹣∠EAF=90°﹣45°=45°,
∴∠EAF=∠E′AF,
在△EAF和△E′AF中,
,
∴△EAF≌△E′AF(SAS),
∴E′F=EF,
∵∠CAB=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠E′CF=45°+45°=90°,
由勾股定理得,E′F2=CE′2+FC2,
即EF2=BE2+FC2,
∵BE=8,CF=6,
∴EF==10.
(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,
∵在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,
∴AB=2,
∴BC===,
∵△AOB绕点B顺时针方向旋转60°,
∴△A′O′B如图所示;
∠A′BC=∠ABC+60°=30°+60°=90°,
∵∠C=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO,
∴△BOO′是等边三角形,
∴BO=OO′,∠BOO′=∠BO′O=60°,
∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°,
∴C、O、A′、O′四点共线,
在Rt△A′BC中,A′C===,
∴OA+OB+OC=A′O′+OO′+OC=A′C=,
∴(OA+OB+OC)2=7,
故答案为:7.
一.选择题(共8小题,满分24分)
1.下列手机中的图标是轴对称图形的是( )
A. B.
C. D.
2.如图,由两个直角三角形和三个大正方形组成的图形,其中阴影部分面积是( )
A.16 B.25 C.144 D.169
3.下列能断定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=2∠B=70°
C.∠A=40°,∠B=70° D.AB=3,BC=6,周长为14
4.如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,则BC的长为( )
A.7cm B.10cm C.12cm D.22cm
5.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.a:b:c=5:12:13
C.a2=b2﹣c2 D.∠A=∠C﹣∠B
6.如图,△ABC中,AB=AC=12,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长是( )
A.20 B.12 C.16 D.13
7.如图,在△ABC中,AB=AC,AD=AE,∠BAD=30°,∠EDC的度数是( )
A.10° B.15° C.20° D.25°
8.如图,点P是长方形ABCD内部的一个动点,已知AB=7,BC=15,若△PBC的面积等于30,则点P到B,C两点距离之和PB+PC的最小值是( )
A.15 B.22 C.18 D.17
二.填空题(共8小题,满分24分)
9.已知△ABC的三边长分别为9、12、15,则最长边上的中线长为 .
10.等腰三角形一腰上的高与另一腰的夹角为50°,那么这个等腰三角形的底角为 .
11.如图,已知AD=DB=BC,∠C=25°,则∠ADE= .
12.若直角三角形两边分别是3和4,则第三边是 .
13.若直角三角形中,一斜边比一直角边大2,且另一直角边长为6,则斜边为 .
14.中国古代称直角三角形为勾股形,其中直角边中较小者为勾,另一长直角边为股,斜边为弦,有一个基本的几何定理,称之为勾股定理.它指直角三角形的两条直角边长(古称勾长、股长)的平方和等于斜边长(古称弦长)的平方.如果设直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么可以用数学语言表达a2+b2=c2,这是一个基本事实.利用这个基本事实解决下列问题.
如图,平安路与幸福路是两条平行的道路,且与新兴大街垂直,老街与小米胡同垂直,书店位于老街与小米胡同的交口处,如果小强同学站在平安路与新兴大街的交叉路口,准备去书店,按图中的街道行走,最近的路程为 m.
15.如图,在Rt△ABC中,∠C=90°,AF=EF.若∠CFE=72°,则∠B= °.
16.如图,已知∠EOF=90°,△ABC中,AC=BC=10,AB=12,点A、B分别在边OE、OF上运动,△ABC的形状大小始终保持不变.在运动的过程中,点C到点O的最大距离为 .
三.解答题(共9小题,满分72分)
17.数学综合实验课上,同学们在测量学校的高度时发现:将旗杆顶端升旗用的绳子垂到地面还多2米;当把绳子的下端拉开拉直后,下端刚好接触地面,测得绳子的下端离开旗杆底端8米,如图,根据以上数据,同学们就可以准确求出旗杆的高度,你知道他们是如何计算出来的吗?
18.如图,一块四边形的土地,其中∠BAD=90°,AB=4m,BC=13m,CD=12m,AD=3m.
(1)试说明BD⊥DC;
(2)求这块土地的面积.
19.在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.
20.如图,一个长方体盒子的长、宽、高分别为9cm,7cm,12cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,那么它爬行的最短路程是多少?
21.如图所示.点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F.
(1)若MN=20cm,求△PEF的周长.
(2)若∠AOB=35°,求∠EPF的度数.
(3)若连接OP,请说明OP平分∠EPF.
22.如图,设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第一根小棒,且A1A2=AA1.
(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)
(2)若已经摆放了3根小棒,则θ1= ,θ2= ,θ3= ;(用含θ的式子表示)
(3)若只能摆放4根小棒,求θ的范围.
23.如图,△ABC中,BE⊥AC,CF⊥AB,垂足分别为E、F,M为BC的中点.
(1)求证:ME=MF.
(2)若∠A=50°,求∠FME的度数.
24.阅读下列材料:在四边形ABCD中,我们把一组邻边相等,剩下另一组邻边也相等的四边形称为筝形,如四边形ABCD中,若两邻边AB=AD,CB=CD,则把这样的四边形称之为筝形.
(1)如图1,在四边形ABCD中,AC同时平分∠BAD和∠BCD.求证:四边形ABCD是筝形.
(2)写出一条关于筝形对角线的性质 ,并利用图1证明此性质.
(3)如图2,在筝形ABCD中,AB=AD=26,BC=DC=25,AC=17,则筝形ABCD的面积为 .
25.(1)阅读理解:如图1,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,求∠APB的大小.
思路点拨:考虑到PA,PB,PC不在一个三角形中,采用转化与化归的数学思想,可以将△ABP绕顶点A逆时针旋转60°到△ACP'处,此时△ACP'≌△ABP,这样,就可以利用全等三角形知识,结合已知条件,将三条线段的长度转化到一个三角形中,从而求出∠APB的度数.请你写出完整的解答过程.
(2)变式拓展:请你利用第(1)问的解答思想方法,解答下面问题:
如图2,在△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,BE=8,CF=6,求EF的大小.
(3)能力提升:如图3,在Rt△ABC中,∠ACB=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,请直接写出(OA+OB+OC)2= .
参考答案
一.选择题(共8小题,满分24分)
1.解:A.不是轴对称图形,故此选项不合题意;
B.不是轴对称图形,故此选项不合题意;
C.是轴对称图形,故此选项符合题意;
D.不是轴对称图形,故此选项不合题意.
故选:C.
2.解:
根据勾股定理得出:AB=,
∴EF=AB=5,
∴阴影部分面积是25,
故选:B.
3.解:A、∠C=180°﹣40°﹣50°=90°,没有相等的角,则不是等腰三角形,本选项错误;
B、∵∠A=2∠B=70°,
∴∠B=35°,
∴∠C=75°,没有相等的角,则不是等腰三角形,本选项错误;
C、∠C=180°﹣40°﹣70°=70°,有相等的角,则是等腰三角形,本选项正确;
D、∵AB=3,BC=6,周长为14,
∴AC=14﹣6﹣3=5,没有相等的边,则不是等腰三角形,本选项错误;
故选:C.
4.解:根据折叠可得:AD=BD,
∵△ADC的周长为17cm,AC=5cm,
∴AD+DC=17﹣5=12(cm),
∵AD=BD,
∴BD+CD=12cm.
即BC=12cm,
故选:C.
5.解:A、∵∠A:∠B:∠C=3:4:5,且∠A+∠B+∠C=180°,可求得∠C≠90°,故△ABC不是直角三角形;
B、不妨设a=5,b=12,c=13,此时a2+b2=132=c2,即a2+b2=c2,故△ABC是直角三角形;
C、由条件可得到a2+c2=b2,满足勾股定理的逆定理,故△ABC是直角三角形;
D、由条件∠A=∠C﹣∠B,且∠A+∠B+∠C=180°,可求得∠C=90°,故△ABC是直角三角形;
故选:A.
6.解:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,CD=BC=4,
∵AD⊥BC,点E为AC的中点,
∴DE=EC=AC=6,
∴△CDE的周长=CD+DE+EC=16,
故选:C.
7.解:设∠EDC=x,∠B=∠C=y,
∠AED=∠EDC+∠C=x+y,
又因为AD=AE,所以∠ADE=∠AED=x+y,
则∠ADC=∠ADE+∠EDC=2x+y,
又因为∠ADC=∠B+∠BAD,
所以 2x+y=y+30,
解得x=15,
所以∠EDC的度数是15°.
故选:B.
8.解:设△BPC中BC边上的高是h,
∵S△PBC=30,BC=15,
∴BC h=30,
∴h=4,
∴动点P在与CB平行且与CB的距离是4的直线l上,
过点B作直线l的对称点B′,连接B′C交直线l于点P,B′C的长就是所求的最短距离之和PB+PC的最小值,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∵BC=15,B′B=8,
∴B′C==17,
故选:D.
二.填空题(共8小题,满分24分)
9.解:∵92+122=225=152,
∴△ABC是直角三角形,
∴最长边上的中线长=×15=7.5.
故答案为:7.5.
10.解:①如图一,
∵△ABC是等腰三角形,BD⊥AC,∠ADB=90°,∠ABD=50°,
∴在直角△ABD中,∠A=90°﹣50°=40°,
∴∠C=∠ABC==70°;
②如图二,
∵△ABC是等腰三角形,BD⊥AC,∠ADB=90°,∠ABD=50°,
∴在直角△ABD中,∠BAD=90°﹣50°=40°,
又∵∠BAD=∠ABC+∠C,∠ABC=∠C,
∴∠C=∠ABC===20°.
故答案为:70°或20°.
11.解:∵DB=BC,∠C=25°,
∴∠BDC=∠C=25°,
∴∠ABD=∠BDC+∠C=50°,
∵AD=DB,
∴∠A=∠ABD=50°,
∴∠ADE=∠A+∠C=50°+25°=75°.
故答案为:75°.
12.解:设第三边为x,
(1)若4是直角边,则第三边x是斜边,由勾股定理得:
32+42=x2,
∴x=5;
(2)若4是斜边,则第三边x为直角边,由勾股定理得:
32+x2=42,
∴x=;
∴第三边的长为5或.
故答案为:5或.
13.解:设一条直角边为a,则斜边为a+2,
∵另一直角边长为6,
∴(a+2)2=a2+62,解得a=8,
∴a+2=8+2=10.
故答案为:10.
14.解:如图所示,设老街与平安路的交点为C,
∵BC∥AD,
∴∠ACB=∠DAE,
∵BC⊥AB,DE⊥AC,
∴∠CBA=∠AED=90°,
在△ABC和△DEA中,
,
∴△ABC≌△DEA(AAS),
∴AE=BC=300 m,
在Rt△ABC中,AC===500(m),
∴CE=AC﹣AE=500﹣300=200(m),
从B到E有两种走法:
①BA+AE=400+300=700(m);
②BC+CE=300+200=500(m),
∴最近的路程是500 m,
故答案为:500.
15.解:∵AF=EF,
∴∠A=∠AEF,
∵∠A+∠AEF=∠CFE=72°,
∴∠A=×72°=36°,
在Rt△ABC中,∠A=36°,
∴∠B=90°﹣36°=54°.
故答案为:54.
16.解:作CD⊥AB于D,连接OD,如图,
∵CA=CB,CD⊥AB,
∴AD=BD=AB=6,
在Rt△ACD中,CD==8,
∵∠AOB=90°,
∴OD=AB=6,
∵OC≤OD+DC(当且仅当C、D、O共线时取等号),
∴OC的最大值为OD+OC=6+8=14,
即点C到点O的最大距离为14.
故答案为14.
三.解答题(共9小题,满分72分)
17.解:设旗杆高x米,则绳子长为(x+2)米,
∵旗杆垂直于地面,
∴旗杆,绳子与地面构成直角三角形,
在Rt△ABC中,AB2+BC2=AC2,
∴x2+82=(x+2)2,
解方程,得x=15,
答:旗杆的高度为15米.
18.解:(1)在Rt△ABD中,∠BAD=90°,AB=4m,AD=3m,由勾股定理得:BD=5m,
∵BC=13m,CD=12m,BD=5m,
∴BD2+DC2=BC2,
∴∠BDC=90°,
即BD⊥DC;
(2)四边形ABCD的面积是S△ABD+S△BDC==36(m2).
19.解:(1)是,
理由是:在△CHB中,
∵CH2+BH2=(2.4)2+(1.8)2=9
BC2=9
∴CH2+BH2=BC2
∴CH⊥AB,
所以CH是从村庄C到河边的最近路
(2)设AC=x
在Rt△ACH中,由已知得AC=x,AH=x﹣1.8,CH=2.4
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣1.8)2+(2.4)2
解这个方程,得x=2.5,
答:原来的路线AC的长为2.5千米.
20.解:①如图1,展开后连接AB,则AB就是在表面上A到B的最短距离,
在Rt△ABM中,由勾股定理得:AB==20(cm);
②如图2,展开后连接AB,则AB就是在表面上A到B的最短距离,
在Rt△ADB中,由勾股定理得:AB==(cm);
③如图3,展开后连接AB,则AB就是在表面上A到B的最短距离,
在Rt△ANB中,由勾股定理得:AB==7(cm).
∴蚂蚁爬行的最短路程是20cm.
21.解:(1)∵点M、N分别是点P关于OA、OB的对称点,
∴ME=PE,NF=PF,MN=20cm,
∴ME+EF+NF=PE+EF+PF=MN=20cm,即△PEF的周长是20cm;
(2)如图,
∵点M、N分别是点P关于直线0A、OB的对称点,
∴OA垂直平分PM,OB垂直平分PN,
∴∠PRE=∠PTF=90°,
∴在四边形OTPR中,
∴∠MPN+∠AOB=180°,
∵∠EPF+2∠M+2∠N=180°,
即∠MPN+∠M+∠N=180°,
∴∠M+∠N=∠AOB=35°,
∴∠EPF=180°﹣35°×2=110°;
(3)如图,连接OM,ON,OP.
∵P,M关于OA对称,
∴OA垂直平分线段PM,
∴OM=OP,EM=EP,
∴∠OPM=∠OMP,∠EPM=∠EMP,
∴∠OPE=∠OME,
同法可证∠OPF=∠ONF,
∵OM=ON,
∴∠OME=∠ONF,
∴∠OPE=∠OPF,
∴OP平分∠EPF.
22.解:(1)小棒不能无限摆下去;
(2)∵小木棒长度都相等,
∴∠BAC=∠AA2A1,∠A2A1A3=∠A2A3A1,∠A3A2A4=∠A3A4A2,
由三角形外角性质,θ1=2θ,θ2=3θ,θ3=4θ;
(3)∵只能摆放4根小木棒,
∴,
解得18°≤θ<22.5°.
故答案为:不能;2θ,3θ,4θ.
23.(1)证明:∵BE⊥AC,CF⊥AB,
∴△BEC为直角三角形,∠BEC=90°,△CFB为直角三角形,∠CFB=90°,
∵M为BC中点,
∴FM=BC,EM=BC,
∴ME=MF;
(2)解:∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵MF=MB,ME=MC,
∴∠MFB=∠ABC,∠MEC=∠ACB,
∴∠BMF+∠CME=360°﹣2×130°=100°,
∴∠FME=180°﹣100°=80°.
24.(1)证明:如图1,∵AC同时平分∠BAD和∠BCD,
∴∠BAC=∠DAC,∠BCA=∠DCA,
∵AC=AC,
∴△BAC≌△DAC(ASA),
∴AB=AD、CB=CD,
∴四边形ABCD是筝形.
(2)筝形有一条对角线垂直平分另一条对角线,
证明:如图1,连接BD,
∵AB=AD,CB=CD,
∴点A、点C都在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC垂直平分BD,
∴筝形有一条对角线垂直平分另一条对角线.
(3)如图2,连接AC交BD于点O,设AO=x,
∵四边形ABCD是筝形,AB=AD=26,BC=DC=25,AC=17,
∴AC垂直线平分BD,CO=17﹣x,
∴∠AOB=∠COB=90°,BO=DO,
∴AB2﹣AO2=BC2﹣CO2=BO2,
∴262﹣x2=252﹣(17﹣x)2,
解得x=10,
∴AO=10,CO=17﹣10=7,
∴BO=DO===24,
∴BD=BO+DO=24+24=48,
∵AO⊥BD,CO⊥BD,
∴S筝形ABCD=BD AO+BD CO=×48×10+×48×7=408,
故答案为:408.
25.解:(1)∵将△ABP绕顶点A逆时针旋转60°到△ACP',
∴△ACP′≌△ABP,
∴AP′=AP=3、CP′=BP=4、∠AP′C=∠APB,
由题意知旋转角∠PAP′=60°,
∴△APP′为等边三角形,
PP′=AP=3,∠AP′P=60°,
易证△PP′C为直角三角形,且∠PP′C=90°,
∴∠APB=∠AP′C=∠AP′P+∠PP′C=60°+90°=150°;
(2)如图2,把△ABE绕点A逆时针旋转90°得到△ACE′,
由旋转的性质得,AE′=AE,CE′=BE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,
∵∠EAF=45°,
∴∠E′AF=∠CAE′+∠CAF=∠BAE+∠CAF=∠BAC﹣∠EAF=90°﹣45°=45°,
∴∠EAF=∠E′AF,
在△EAF和△E′AF中,
,
∴△EAF≌△E′AF(SAS),
∴E′F=EF,
∵∠CAB=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠E′CF=45°+45°=90°,
由勾股定理得,E′F2=CE′2+FC2,
即EF2=BE2+FC2,
∵BE=8,CF=6,
∴EF==10.
(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,
∵在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,
∴AB=2,
∴BC===,
∵△AOB绕点B顺时针方向旋转60°,
∴△A′O′B如图所示;
∠A′BC=∠ABC+60°=30°+60°=90°,
∵∠C=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO,
∴△BOO′是等边三角形,
∴BO=OO′,∠BOO′=∠BO′O=60°,
∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°,
∴C、O、A′、O′四点共线,
在Rt△A′BC中,A′C===,
∴OA+OB+OC=A′O′+OO′+OC=A′C=,
∴(OA+OB+OC)2=7,
故答案为:7.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
