2023-2024学年人教版九年级数学上册第二十二章二次函数单元复习题(含解析)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册第二十二章二次函数单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 476.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-07 13:29:59 | ||
图片预览




文档简介
人教版九年级数学上册第二十二章二次函数单元复习题
一、选择题
1.下列函数是二次函数的是( )
A.y=2x B. C. D.
2.已知抛物线的开口向下,则a的值可能为( )
A.-2 B. C.1 D.
3.抛物线的顶点坐标是( )
A. B. C. D.
4.关于x的二次函数在y轴右侧y随x的增大而减小,则a的范围为( )
A. B. C. D.
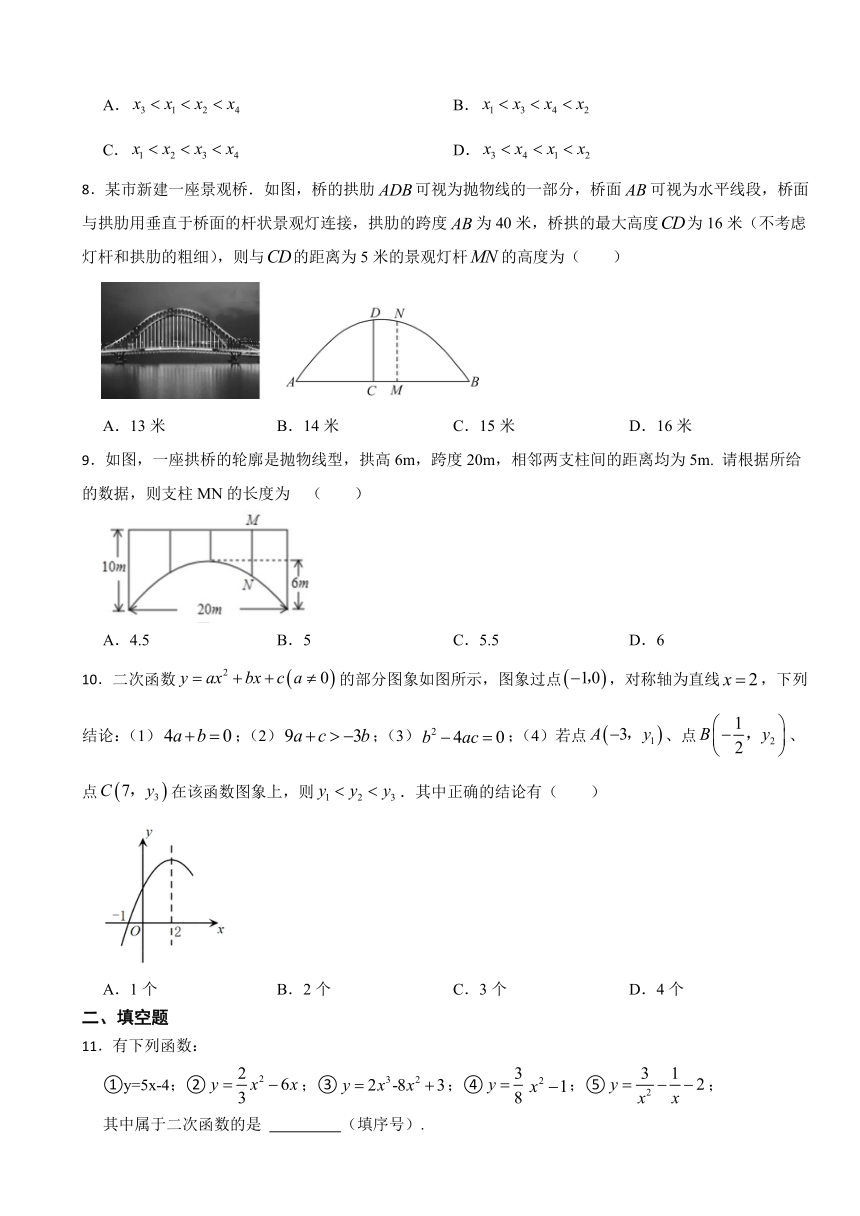
5.在平面直角坐标系xOy中,二次函数y=﹣x2+1的大致图象是( )
A. B.
C. D.
6.已知二次函数的图象如图所示,当时,的取值范围是( )
A. B.
C. D.或
7.已知,若关于x的方程的解为.关于x的方程的解为.则下列结论正确的是( )
A. B.
C. D.
8.某市新建一座景观桥.如图,桥的拱肋可视为抛物线的一部分,桥面可视为水平线段,桥面与拱肋用垂直于桥面的杆状景观灯连接,拱肋的跨度为40米,桥拱的最大高度为16米(不考虑灯杆和拱肋的粗细),则与的距离为5米的景观灯杆的高度为( )
A.13米 B.14米 C.15米 D.16米
9.如图,一座拱桥的轮廓是抛物线型,拱高6m,跨度20m,相邻两支柱间的距离均为5m. 请根据所给的数据,则支柱MN的长度为 ( )
A.4.5 B.5 C.5.5 D.6
10.二次函数的部分图象如图所示,图象过点,对称轴为直线,下列结论:(1);(2);(3);(4)若点、点、点在该函数图象上,则.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.有下列函数:
①y=5x-4;②;③;④;⑤;
其中属于二次函数的是 (填序号).
12.已知点,,都在二次函数的图象上,则、、的大小关系是 .(用“<”表示)
13.已知二次函数的部分图象如下图所示,则关于的一元二次方程的解为 .
14.从地面竖直向上抛出一小球,小球的高度h(单位:米)与小球运动时间t(单位:秒)的函数关系式是.小球抛出 秒后开始下落.
三、解答题
15.已知y=(m﹣1)x 是关于x的二次函数,求m的值.
16.已知二次函数的图象的顶点在x轴下方,求实数k的取值范围.
17.若二次函数的对称轴为直线,求关于x的方程的解.
18.为实施“乡村振兴”计划,某村产业合作社种植了“千亩桃园”.2022年该村桃子丰收,销售前对本地市场进行调查发现:当批发价为4千元/吨时,每天可售出12吨,每吨涨1千元,每天销量将减少2吨,据推测,每吨平均投入成本2千元,为了抢占市场,薄利多销,该村产业合作社决定,批发价每吨不低于4千元,不高于5.5千元.请解答以下问题:
(1)求每天销量y(吨)与批发价x(千元/吨)之间的函数关系式;
(2)当批发价定为多少时,每天所获利润最大?最大利润是多少?
四、综合题
19.已知二次函数
(1)求二次函数图象的顶点坐标(用含的代数式表示);
(2)在平面直角坐标系中,若二次函数的图象与轴交于两点,,且图象过四点,直接写出的大小关系.
(3)点是二次函数图象上的一个动点,当时,的取值范围是,求二次函数的表达式.
20.已知二次函数 的部分图象如图所示,
(1)求该二次函数图象的对称轴,并利用图象直接写出一元二次方程 的解.
(2)向上平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式。
21.如图,在一个边长为的正方形的四个角上,都剪去一个大小相同的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)若小正方形的边长为,图中阴影部分的面积为,请直接写出y与x之间的关系式;并求出当时,图中阴影部分的面积.
22.已知抛物线:
(1)若抛物线经过原点,则的值为 ,此时抛物线的顶点坐标为 .
(2)用含的代数式表示抛物线的顶点坐标,并说明无论为何值,抛物线的顶点都在同一条抛物线上.
(3)无论为何值,抛物线一定恒过定点,设抛物线的顶点为,当点不与点重合时,过点作E轴,与抛物线的另一个交点为,过点作轴,与抛物线的另一个交点为.求证:四边形是平行四边形.
答案解析部分
1.【答案】C
【解析】【解答】解:A、该函数不符合二次函数的定义,故本选项不正确;
B、该函数不符合二次函数的定义,故本选项不正确;
C、该函数符合二次函数的定义,故本选项正确;
D、该函数的右边不是整式,它不是二次函数,故本选项不正确.
故答案为:C.
【分析】形如“y=ax2+bx+c(a、b、c是常数,且a≠0)”的函数就是二次函数,据此一一判断得出答案.
2.【答案】A
【解析】【解答】解:抛物线y=ax2(a≠0)的开口向下,
∴a<0,
故只有A选项符合题意.
故答案为:A.
【分析】抛物线y=ax2(a≠0),当a>0时,抛物线的开口向上,当a<0时,抛物线的开口向下,据此一一判断得出答案.
3.【答案】B
【解析】【解答】 抛物线的顶点坐标, 横坐标是2,纵坐标是1.
故选:B
【分析】抛物线顶点式解析式,直接读取顶点坐标,横坐标是平方项中“x-”后面的数h,即2;纵坐标是k,即1.
4.【答案】B
【解析】【解答】解:关于x的二次函数的对称轴为直线,
∵,且在y轴右侧y随x的增大而减小,
∴,
解得:,故B正确.
故答案为:B.
【分析】首先根据二次函数对称轴直线公式求出对称轴直线为,由于二次项系数a=-1<0,且在y轴右侧y随x的增大而减小,所以可得对称轴直线在y轴左侧或与y轴重合,即,求解即可得出a的取值范围,从而得出答案.
5.【答案】A
【解析】【解答】解:在y=-x2+1中,
∵a=-1<0,
∴抛物线的开口向下,
∵顶点坐标为(0,1),
∴对称轴为为y轴,
故二次函数y=-x2+1的大致图象是A选项,
故答案为:A.
【分析】根据二次函数的解析式,当a>0时,抛物线开口向上;当a<0时,抛物线开口向下;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);得到抛物线的开口向下,顶点坐标为(0,1),对称轴为为y轴,于是得到结论.
6.【答案】A
【解析】【解答】如图: 二次函数的图象 ,与x轴有2个交点(2,0)和(-1,0),
开口向上,
∴当时,
当x=-1和2时,y=0
当时,
根据题意x取值:
故选:A
【分析】根据二次函数图象与一元二次方程的关系,可以从图中直接读取x的取值范围。x轴下方的图象x值就是y小于0时x的全部取值。
7.【答案】B
【解析】【解答】解:如图所示:设直线y=m与抛物线 交于A、B两点,直线y=n与抛物线 交于C、D两点,
∵,关于x的方程的解为.关于x的方程的解为,
∴,
故答案为:B.
【分析】先作图,再结合题意,比较大小即可。
8.【答案】C
【解析】【解答】解:如图,以AB所在的直线为x轴,CD所在的直线为y轴,建立平面直角坐标系,
由题意知点B(20,0),顶点D(0,16),
设抛物线的解析式为y=ax2+16,
将(20,0)代入得400a+16=0,解得a=,
∴所求的函数解析式为:y=x2+16,
当x=5时,y=15,
∴与CD距离为15米的景观灯杆MN的高度为15米.
故答案为:C.
【分析】以AB所在的直线为x轴,CD所在的直线为y轴,建立平面直角坐标系,由题意知点B(20,0),顶点D(0,16),设抛物线的解析式为y=ax2+16,将点B的坐标代入可求出a的值,从而得到所求的抛物线的解析式,进而将x=5代入所求的抛物线的解析式算出对应的y的值,即可得出答案.
9.【答案】C
【解析】【解答】解:建立平面直角坐标系如下,
∵拱高6m,跨度20m,
∴点B(0,6),点A(10,0)
设抛物线的解析式为y=ax2+6,
∴100a+6=0
解之:
∴抛物线的解析式为;
∵相邻两支柱间的距离均为5m ,
∴点N的横坐标为5,
∴,
∴MN=10-4.5=5.5.
故答案为:C
【分析】先建立平面直角坐标系,利用已知可得到点D和点A的坐标,因此设抛物线的解析式为y=ax2+6,将点A的坐标代入求出a的值,即可得到抛物线的解析式,再将x=5代入求出对应得y的值,可得到点N的坐标,然后求出MN的长.
10.【答案】B
【解析】【解答】∵x=﹣=2,
∴4a+b=0,故(1)正确.
由函数图象可知:函数图象与x轴有两个交点,
∴b2﹣4ac>0,故(3)错误.
∵抛物线与x轴的一个交点为(﹣1,0),对称轴为直线x=2,
∴另一个交点为(5,0),
∴当x=3时,y>0,
∴9a+3b+c>0,
∴9a+c>﹣3b,
故(2)正确;
∵抛物线的对称轴为x=2,C(7,y3),
∴(﹣3,y3).
∵﹣3<﹣,在对称轴的左侧,
∴y随x的增大而增大,
∴y1=y3<y2,故(4)错误.
故答案为: B
【分析】根据抛物线的对称轴为直线x=2,则有4a+b=0;观察函数图象得到当x=3时,函数值大于0,则9a+3b+c>0,即9a+c>﹣3b;利用抛物线的对称性得到(﹣3,y3),然后利用二次函数的增减性求解即可,作出直线y=﹣3,然后依据函数图象进行判断即可。
11.【答案】②④
【解析】【解答】解:②y=;④y=﹣1符合二次函数的定义,属于二次函数;
①y=5x﹣4是一次函数,不属于二次函数;
③y=自变量的最高次数是3,不属于二次函数;
⑤y=的右边不是整式,不属于二次函数.
综上所述,其中属于二次函数的是②④.
故答案为:②④.
【分析】形如“y=ax2+bx+c(a、b、c是常数,且a≠0)”的函数就是二次函数,据此一一判断得出答案.
12.【答案】
【解析】【解答】解:二次函数的图象的对称轴为直线x=2,
因为点到直线的距离最小,点到直线的距离最大,且抛物线的开口向上,
所以.
故答案为:.
【分析】利用二次函数的性质求解即可。
13.【答案】,
【解析】【解答】解:由图可知, 二次函数 经过点(3,0),
∴-9+6+m=0,
∴m=3.
将m代入 中,
∴,
∴,
∴,
∴.
故答案为:,.
【分析】观察图像,由图可知二次函数经过(3,0),将其代入中即可求出m的值,从而求出对应方程的解.
14.【答案】1
【解析】【解答】解: -4.9(t-1)2+4.9,
∴当小球抛出1秒后开始下落.
故答案为:1.
【分析】当小球达到最高点时开始下落,将函数解析式化为顶点式,即可得解.
15.【答案】解:∵y=(m﹣1)x 是关于x的二次函数,
∴m2+2m﹣1=2,
解得m=1或﹣3,
∵m﹣1≠0,
∴m≠1,
∴m=﹣3.
【解析】【分析】根据二次函数定义可得m2+2m﹣1=2且m﹣1≠0,再解即可.
16.【答案】解:将改为顶点式为:,
∴其顶点坐标为(2,k-4).
∵顶点在x轴下方,
∴k-4<0,
∴k<4.
【解析】【分析】先求出 , 再求出 其顶点坐标为(2,k-4),最后求解即可。
17.【答案】解:∵二次函数的对称轴为直线,
∴,
解得.
将代入中,得:,
解得,.
【解析】【分析】利用二次函数的对称轴公式即可算出b的值,将求得的b代入方程,用因式分解法解关于x的一元二次方程即可.
18.【答案】(1)解:根据题意得y=12-2(x-4)=-6x+20(4≤x≤5.5),
所以每天销量y(吨)与批发价x(千元/吨)之间的函数关系式y=-2x+20,
自变量x的取值范围是4≤x≤5.5;
(2)解:设每天获得的利润为W千元,根据题意得w=(-2x+20)(x-2)=﹣2x2+24x-40=-2(x-6)2+32,
∵﹣6<0,
∴当x<6,w随x的增大而增大.
∵4≤x≤5.5,
∴当x=5.5时,w有最大值 -2×(5.5-6)2+32=31.5 ,
∴将批发价定为5.5千元时,每天获得的利润最大为31.5.
【解析】【分析】 (1)根据题意直接写出y与x之间的函数关系式和自变量的取值范围;
(2)根据销售利润=销售量×(批发价-成本价),列出销售利润w(千元)与批发价x(千元/吨)之间的函数关系式,再依据函数的增减性求得最大利润.
19.【答案】(1)解:∵,
∴二次函数图象的顶点坐标为;
(2)解:.
(3)解:当时,抛物线开口向上,时,随增大而增大,
∴当时,,当时,,
∴,
解得,
∴,
当时,抛物线开口向下,时,随增大而减小,
∴当时,,当时,,
∴,
解得,
∴,
综上所述,或.
【解析】【解答】解:(2)由(1)得抛物线对称轴为直线,
当时,抛物线开口向上,
∵,
∴,
当时,抛物线开口向下,
∵,
∴.
【分析】(1)将二次函数解析式化为顶点式求解.
(2)分类讨论a>0,a<0,根据抛物线对称轴及抛物线开口方向求解.
(3)分类讨论a>0,a<0,由抛物线开口向上可得m=﹣2时,n=﹣1,m=1时,n=1,由抛物线开口向下可得m=﹣2时,n=1,m=1时,n=﹣1,进而求解.
20.【答案】(1)解:由题可得该二次函数图象的对称轴为直线 , 方程的解为 .
(2)解:由 (1) 可得二次函数的表达式为 ,
所以平移后图象所对应的二次函数的表达式为 .
【解析】【分析】(1)直接利用对称轴公式,即可写出对称轴,再利用图中与x轴的交点坐标(1,0),以及两交点关于对称轴对称,即可求得另一交点坐标,两交点的横坐标,即为所求的解;
(2)根据(1)易得二次函数解析式为,令平移后的解析式为,代入(0,0)求出n的值即可.
21.【答案】(1)解:自变量是小正方形的边长,因变量是图中阴影部分的面积;
(2)解:由题意可得,
当时,,
所以当时,图中阴影部分的面积为.
【解析】【分析】(1)根据自变量和因变量的定义判断求解即可;
(2)根据题意先求出 , 再将x=3代入计算求解即可。
22.【答案】(1);
(2)解:∵y=x2-2mx+2m+1=(x-m)2-m2+2m+1,
∴顶点坐标为(m,-m2+2m+1).
令x=m,则y=-x2+2x+1,
∴抛物线C的顶点在y=-x2+2x+1上.
(3)证明:,
当时,,即点,
抛物线的部分图象的示意图如下所示:
由(2)知,点,点,
则,
当时,则,
整理得:,
则,
∵,则,
则,
而轴,
故四边形是平行四边形.
【解析】【解答】解:(1)将(0,0)代入可得0=2m+1,
解得m=,
∴y=x2+x=(x+)2-,
∴顶点坐标为(-,-).
【分析】(1)将(0,0)代入可求出m的值,据此可得抛物线的解析式,然后将其化为顶点式,进而可得顶点坐标;
(2)将抛物线解析式化为顶点式,可得顶点坐标,据此解答;
(3)易得A(1,2),B(m,-m2+2m+1),则AE=2(1-m),令y=-m2+2m+1,可得x2-2x+2m-m2=0,根据根与系数的关系可得x1x2=m(2-m),则BD=2-2m=AE,然后根据平行四边形的判定定理进行证明.
一、选择题
1.下列函数是二次函数的是( )
A.y=2x B. C. D.
2.已知抛物线的开口向下,则a的值可能为( )
A.-2 B. C.1 D.
3.抛物线的顶点坐标是( )
A. B. C. D.
4.关于x的二次函数在y轴右侧y随x的增大而减小,则a的范围为( )
A. B. C. D.
5.在平面直角坐标系xOy中,二次函数y=﹣x2+1的大致图象是( )
A. B.
C. D.
6.已知二次函数的图象如图所示,当时,的取值范围是( )
A. B.
C. D.或
7.已知,若关于x的方程的解为.关于x的方程的解为.则下列结论正确的是( )
A. B.
C. D.
8.某市新建一座景观桥.如图,桥的拱肋可视为抛物线的一部分,桥面可视为水平线段,桥面与拱肋用垂直于桥面的杆状景观灯连接,拱肋的跨度为40米,桥拱的最大高度为16米(不考虑灯杆和拱肋的粗细),则与的距离为5米的景观灯杆的高度为( )
A.13米 B.14米 C.15米 D.16米
9.如图,一座拱桥的轮廓是抛物线型,拱高6m,跨度20m,相邻两支柱间的距离均为5m. 请根据所给的数据,则支柱MN的长度为 ( )
A.4.5 B.5 C.5.5 D.6
10.二次函数的部分图象如图所示,图象过点,对称轴为直线,下列结论:(1);(2);(3);(4)若点、点、点在该函数图象上,则.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.有下列函数:
①y=5x-4;②;③;④;⑤;
其中属于二次函数的是 (填序号).
12.已知点,,都在二次函数的图象上,则、、的大小关系是 .(用“<”表示)
13.已知二次函数的部分图象如下图所示,则关于的一元二次方程的解为 .
14.从地面竖直向上抛出一小球,小球的高度h(单位:米)与小球运动时间t(单位:秒)的函数关系式是.小球抛出 秒后开始下落.
三、解答题
15.已知y=(m﹣1)x 是关于x的二次函数,求m的值.
16.已知二次函数的图象的顶点在x轴下方,求实数k的取值范围.
17.若二次函数的对称轴为直线,求关于x的方程的解.
18.为实施“乡村振兴”计划,某村产业合作社种植了“千亩桃园”.2022年该村桃子丰收,销售前对本地市场进行调查发现:当批发价为4千元/吨时,每天可售出12吨,每吨涨1千元,每天销量将减少2吨,据推测,每吨平均投入成本2千元,为了抢占市场,薄利多销,该村产业合作社决定,批发价每吨不低于4千元,不高于5.5千元.请解答以下问题:
(1)求每天销量y(吨)与批发价x(千元/吨)之间的函数关系式;
(2)当批发价定为多少时,每天所获利润最大?最大利润是多少?
四、综合题
19.已知二次函数
(1)求二次函数图象的顶点坐标(用含的代数式表示);
(2)在平面直角坐标系中,若二次函数的图象与轴交于两点,,且图象过四点,直接写出的大小关系.
(3)点是二次函数图象上的一个动点,当时,的取值范围是,求二次函数的表达式.
20.已知二次函数 的部分图象如图所示,
(1)求该二次函数图象的对称轴,并利用图象直接写出一元二次方程 的解.
(2)向上平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式。
21.如图,在一个边长为的正方形的四个角上,都剪去一个大小相同的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
(1)在这个变化过程中,自变量、因变量各是什么?
(2)若小正方形的边长为,图中阴影部分的面积为,请直接写出y与x之间的关系式;并求出当时,图中阴影部分的面积.
22.已知抛物线:
(1)若抛物线经过原点,则的值为 ,此时抛物线的顶点坐标为 .
(2)用含的代数式表示抛物线的顶点坐标,并说明无论为何值,抛物线的顶点都在同一条抛物线上.
(3)无论为何值,抛物线一定恒过定点,设抛物线的顶点为,当点不与点重合时,过点作E轴,与抛物线的另一个交点为,过点作轴,与抛物线的另一个交点为.求证:四边形是平行四边形.
答案解析部分
1.【答案】C
【解析】【解答】解:A、该函数不符合二次函数的定义,故本选项不正确;
B、该函数不符合二次函数的定义,故本选项不正确;
C、该函数符合二次函数的定义,故本选项正确;
D、该函数的右边不是整式,它不是二次函数,故本选项不正确.
故答案为:C.
【分析】形如“y=ax2+bx+c(a、b、c是常数,且a≠0)”的函数就是二次函数,据此一一判断得出答案.
2.【答案】A
【解析】【解答】解:抛物线y=ax2(a≠0)的开口向下,
∴a<0,
故只有A选项符合题意.
故答案为:A.
【分析】抛物线y=ax2(a≠0),当a>0时,抛物线的开口向上,当a<0时,抛物线的开口向下,据此一一判断得出答案.
3.【答案】B
【解析】【解答】 抛物线的顶点坐标, 横坐标是2,纵坐标是1.
故选:B
【分析】抛物线顶点式解析式,直接读取顶点坐标,横坐标是平方项中“x-”后面的数h,即2;纵坐标是k,即1.
4.【答案】B
【解析】【解答】解:关于x的二次函数的对称轴为直线,
∵,且在y轴右侧y随x的增大而减小,
∴,
解得:,故B正确.
故答案为:B.
【分析】首先根据二次函数对称轴直线公式求出对称轴直线为,由于二次项系数a=-1<0,且在y轴右侧y随x的增大而减小,所以可得对称轴直线在y轴左侧或与y轴重合,即,求解即可得出a的取值范围,从而得出答案.
5.【答案】A
【解析】【解答】解:在y=-x2+1中,
∵a=-1<0,
∴抛物线的开口向下,
∵顶点坐标为(0,1),
∴对称轴为为y轴,
故二次函数y=-x2+1的大致图象是A选项,
故答案为:A.
【分析】根据二次函数的解析式,当a>0时,抛物线开口向上;当a<0时,抛物线开口向下;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);得到抛物线的开口向下,顶点坐标为(0,1),对称轴为为y轴,于是得到结论.
6.【答案】A
【解析】【解答】如图: 二次函数的图象 ,与x轴有2个交点(2,0)和(-1,0),
开口向上,
∴当时,
当x=-1和2时,y=0
当时,
根据题意x取值:
故选:A
【分析】根据二次函数图象与一元二次方程的关系,可以从图中直接读取x的取值范围。x轴下方的图象x值就是y小于0时x的全部取值。
7.【答案】B
【解析】【解答】解:如图所示:设直线y=m与抛物线 交于A、B两点,直线y=n与抛物线 交于C、D两点,
∵,关于x的方程的解为.关于x的方程的解为,
∴,
故答案为:B.
【分析】先作图,再结合题意,比较大小即可。
8.【答案】C
【解析】【解答】解:如图,以AB所在的直线为x轴,CD所在的直线为y轴,建立平面直角坐标系,
由题意知点B(20,0),顶点D(0,16),
设抛物线的解析式为y=ax2+16,
将(20,0)代入得400a+16=0,解得a=,
∴所求的函数解析式为:y=x2+16,
当x=5时,y=15,
∴与CD距离为15米的景观灯杆MN的高度为15米.
故答案为:C.
【分析】以AB所在的直线为x轴,CD所在的直线为y轴,建立平面直角坐标系,由题意知点B(20,0),顶点D(0,16),设抛物线的解析式为y=ax2+16,将点B的坐标代入可求出a的值,从而得到所求的抛物线的解析式,进而将x=5代入所求的抛物线的解析式算出对应的y的值,即可得出答案.
9.【答案】C
【解析】【解答】解:建立平面直角坐标系如下,
∵拱高6m,跨度20m,
∴点B(0,6),点A(10,0)
设抛物线的解析式为y=ax2+6,
∴100a+6=0
解之:
∴抛物线的解析式为;
∵相邻两支柱间的距离均为5m ,
∴点N的横坐标为5,
∴,
∴MN=10-4.5=5.5.
故答案为:C
【分析】先建立平面直角坐标系,利用已知可得到点D和点A的坐标,因此设抛物线的解析式为y=ax2+6,将点A的坐标代入求出a的值,即可得到抛物线的解析式,再将x=5代入求出对应得y的值,可得到点N的坐标,然后求出MN的长.
10.【答案】B
【解析】【解答】∵x=﹣=2,
∴4a+b=0,故(1)正确.
由函数图象可知:函数图象与x轴有两个交点,
∴b2﹣4ac>0,故(3)错误.
∵抛物线与x轴的一个交点为(﹣1,0),对称轴为直线x=2,
∴另一个交点为(5,0),
∴当x=3时,y>0,
∴9a+3b+c>0,
∴9a+c>﹣3b,
故(2)正确;
∵抛物线的对称轴为x=2,C(7,y3),
∴(﹣3,y3).
∵﹣3<﹣,在对称轴的左侧,
∴y随x的增大而增大,
∴y1=y3<y2,故(4)错误.
故答案为: B
【分析】根据抛物线的对称轴为直线x=2,则有4a+b=0;观察函数图象得到当x=3时,函数值大于0,则9a+3b+c>0,即9a+c>﹣3b;利用抛物线的对称性得到(﹣3,y3),然后利用二次函数的增减性求解即可,作出直线y=﹣3,然后依据函数图象进行判断即可。
11.【答案】②④
【解析】【解答】解:②y=;④y=﹣1符合二次函数的定义,属于二次函数;
①y=5x﹣4是一次函数,不属于二次函数;
③y=自变量的最高次数是3,不属于二次函数;
⑤y=的右边不是整式,不属于二次函数.
综上所述,其中属于二次函数的是②④.
故答案为:②④.
【分析】形如“y=ax2+bx+c(a、b、c是常数,且a≠0)”的函数就是二次函数,据此一一判断得出答案.
12.【答案】
【解析】【解答】解:二次函数的图象的对称轴为直线x=2,
因为点到直线的距离最小,点到直线的距离最大,且抛物线的开口向上,
所以.
故答案为:.
【分析】利用二次函数的性质求解即可。
13.【答案】,
【解析】【解答】解:由图可知, 二次函数 经过点(3,0),
∴-9+6+m=0,
∴m=3.
将m代入 中,
∴,
∴,
∴,
∴.
故答案为:,.
【分析】观察图像,由图可知二次函数经过(3,0),将其代入中即可求出m的值,从而求出对应方程的解.
14.【答案】1
【解析】【解答】解: -4.9(t-1)2+4.9,
∴当小球抛出1秒后开始下落.
故答案为:1.
【分析】当小球达到最高点时开始下落,将函数解析式化为顶点式,即可得解.
15.【答案】解:∵y=(m﹣1)x 是关于x的二次函数,
∴m2+2m﹣1=2,
解得m=1或﹣3,
∵m﹣1≠0,
∴m≠1,
∴m=﹣3.
【解析】【分析】根据二次函数定义可得m2+2m﹣1=2且m﹣1≠0,再解即可.
16.【答案】解:将改为顶点式为:,
∴其顶点坐标为(2,k-4).
∵顶点在x轴下方,
∴k-4<0,
∴k<4.
【解析】【分析】先求出 , 再求出 其顶点坐标为(2,k-4),最后求解即可。
17.【答案】解:∵二次函数的对称轴为直线,
∴,
解得.
将代入中,得:,
解得,.
【解析】【分析】利用二次函数的对称轴公式即可算出b的值,将求得的b代入方程,用因式分解法解关于x的一元二次方程即可.
18.【答案】(1)解:根据题意得y=12-2(x-4)=-6x+20(4≤x≤5.5),
所以每天销量y(吨)与批发价x(千元/吨)之间的函数关系式y=-2x+20,
自变量x的取值范围是4≤x≤5.5;
(2)解:设每天获得的利润为W千元,根据题意得w=(-2x+20)(x-2)=﹣2x2+24x-40=-2(x-6)2+32,
∵﹣6<0,
∴当x<6,w随x的增大而增大.
∵4≤x≤5.5,
∴当x=5.5时,w有最大值 -2×(5.5-6)2+32=31.5 ,
∴将批发价定为5.5千元时,每天获得的利润最大为31.5.
【解析】【分析】 (1)根据题意直接写出y与x之间的函数关系式和自变量的取值范围;
(2)根据销售利润=销售量×(批发价-成本价),列出销售利润w(千元)与批发价x(千元/吨)之间的函数关系式,再依据函数的增减性求得最大利润.
19.【答案】(1)解:∵,
∴二次函数图象的顶点坐标为;
(2)解:.
(3)解:当时,抛物线开口向上,时,随增大而增大,
∴当时,,当时,,
∴,
解得,
∴,
当时,抛物线开口向下,时,随增大而减小,
∴当时,,当时,,
∴,
解得,
∴,
综上所述,或.
【解析】【解答】解:(2)由(1)得抛物线对称轴为直线,
当时,抛物线开口向上,
∵,
∴,
当时,抛物线开口向下,
∵,
∴.
【分析】(1)将二次函数解析式化为顶点式求解.
(2)分类讨论a>0,a<0,根据抛物线对称轴及抛物线开口方向求解.
(3)分类讨论a>0,a<0,由抛物线开口向上可得m=﹣2时,n=﹣1,m=1时,n=1,由抛物线开口向下可得m=﹣2时,n=1,m=1时,n=﹣1,进而求解.
20.【答案】(1)解:由题可得该二次函数图象的对称轴为直线 , 方程的解为 .
(2)解:由 (1) 可得二次函数的表达式为 ,
所以平移后图象所对应的二次函数的表达式为 .
【解析】【分析】(1)直接利用对称轴公式,即可写出对称轴,再利用图中与x轴的交点坐标(1,0),以及两交点关于对称轴对称,即可求得另一交点坐标,两交点的横坐标,即为所求的解;
(2)根据(1)易得二次函数解析式为,令平移后的解析式为,代入(0,0)求出n的值即可.
21.【答案】(1)解:自变量是小正方形的边长,因变量是图中阴影部分的面积;
(2)解:由题意可得,
当时,,
所以当时,图中阴影部分的面积为.
【解析】【分析】(1)根据自变量和因变量的定义判断求解即可;
(2)根据题意先求出 , 再将x=3代入计算求解即可。
22.【答案】(1);
(2)解:∵y=x2-2mx+2m+1=(x-m)2-m2+2m+1,
∴顶点坐标为(m,-m2+2m+1).
令x=m,则y=-x2+2x+1,
∴抛物线C的顶点在y=-x2+2x+1上.
(3)证明:,
当时,,即点,
抛物线的部分图象的示意图如下所示:
由(2)知,点,点,
则,
当时,则,
整理得:,
则,
∵,则,
则,
而轴,
故四边形是平行四边形.
【解析】【解答】解:(1)将(0,0)代入可得0=2m+1,
解得m=,
∴y=x2+x=(x+)2-,
∴顶点坐标为(-,-).
【分析】(1)将(0,0)代入可求出m的值,据此可得抛物线的解析式,然后将其化为顶点式,进而可得顶点坐标;
(2)将抛物线解析式化为顶点式,可得顶点坐标,据此解答;
(3)易得A(1,2),B(m,-m2+2m+1),则AE=2(1-m),令y=-m2+2m+1,可得x2-2x+2m-m2=0,根据根与系数的关系可得x1x2=m(2-m),则BD=2-2m=AE,然后根据平行四边形的判定定理进行证明.
同课章节目录
