2023—2024学年北师大版数学八年级上册第3章位置与坐标 单元综合练习题(含解析)
文档属性
| 名称 | 2023—2024学年北师大版数学八年级上册第3章位置与坐标 单元综合练习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 304.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-07 13:43:38 | ||
图片预览



文档简介
2023-2024学年北师大版八年级数学上册《第3章位置与坐标》单元综合练习题(附答案)
一、选择题
1.已知点P(2,﹣3),则点P关于y轴对称点P′的坐标为( )
A.(﹣2,﹣3) B.(﹣2,3) C.(2,﹣3) D.(2,3)
2.在平面直角坐标系中,点(0,﹣2)在( )
A.x轴上 B.y轴上 C.第三象限 D.第四象限
3.如果P(a,b)在第三象限,那么点Q(a+b,ab)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.点P(﹣1,3)关于x轴对称的点的坐标是( )
A.(﹣1,﹣3) B.(1,﹣3) C.(1,3) D.(﹣3,1)
5.点A(m+1,3m﹣7)在第一、三象限的角平分线上,则m的值为( )
A.3 B.4 C.5 D.6
6.如图,点A(1,﹣2)与点B(a,b)关于直线l对称,则a﹣b的值为( )
A.1 B.﹣1 C.2 D.﹣5
7.若点P(m+1,4﹣2m)在第一、三象限的平分线上,则点P的坐标为( )
A.(2,2) B.(6,﹣6) C.(﹣2,﹣2) D.(6,6)
8.已知A(﹣4,0)和B(0,b)两点,若直线AB与两坐标轴围成的三角形的面积为6,则b的值为( )
A.6 B.6或﹣6 C.3 D.3或﹣3
9.在平面直角坐标系中有一个长方形,其中三个顶点的坐标分别为(﹣2,2),(1,2),(1,﹣2),则第四个顶点的坐标为( )
A.(﹣1,2) B.(1,﹣1) C.(2,﹣2) D.(﹣2,﹣2)
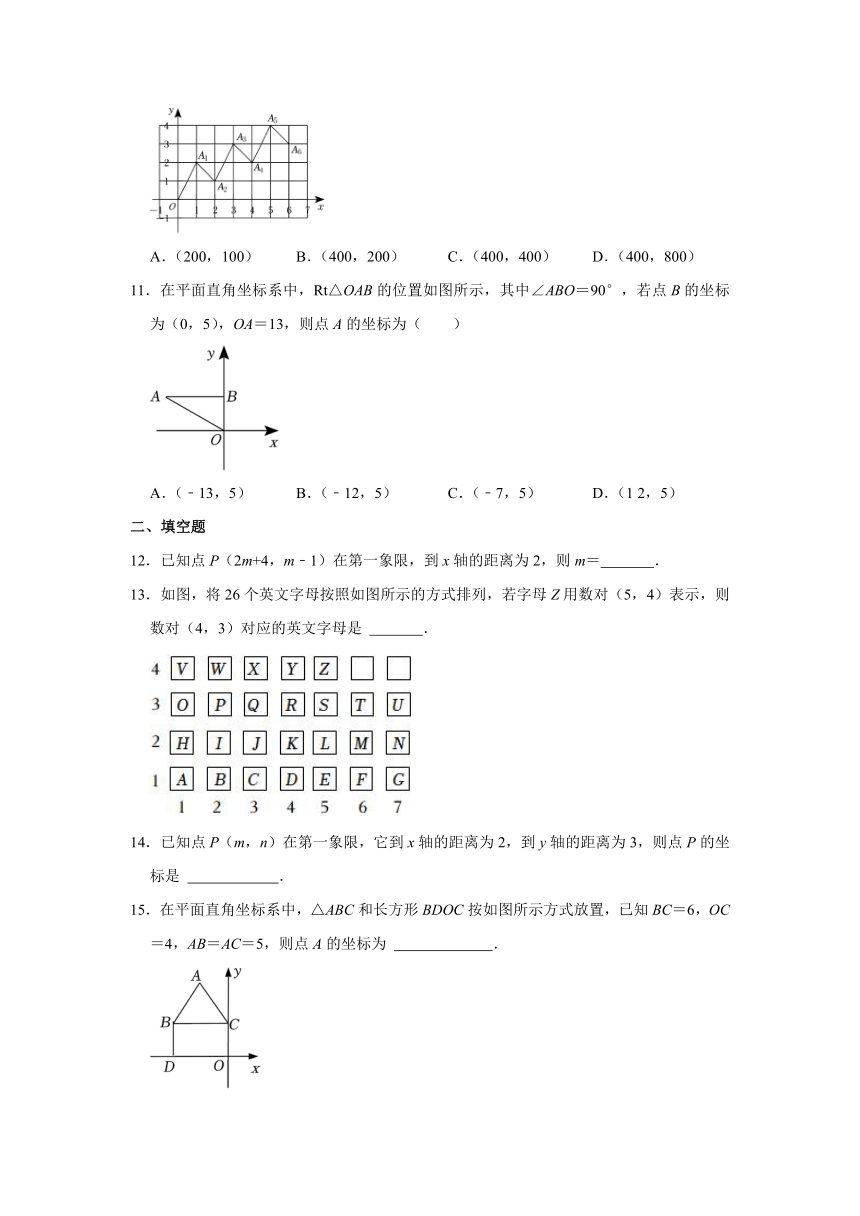
10.如图,在平面直角坐标系中,已知A1(1,2),A2(2,1),A3(3,3),A4(4,2),A5(5,4),A6(6,3),…,以此类推,A400的坐标为( )
A.(200,100) B.(400,200) C.(400,400) D.(400,800)
11.在平面直角坐标系中,Rt△OAB的位置如图所示,其中∠ABO=90°,若点B的坐标为(0,5),OA=13,则点A的坐标为( )
A.(﹣13,5) B.(﹣12,5) C.(﹣7,5) D.(1 2,5)
二、填空题
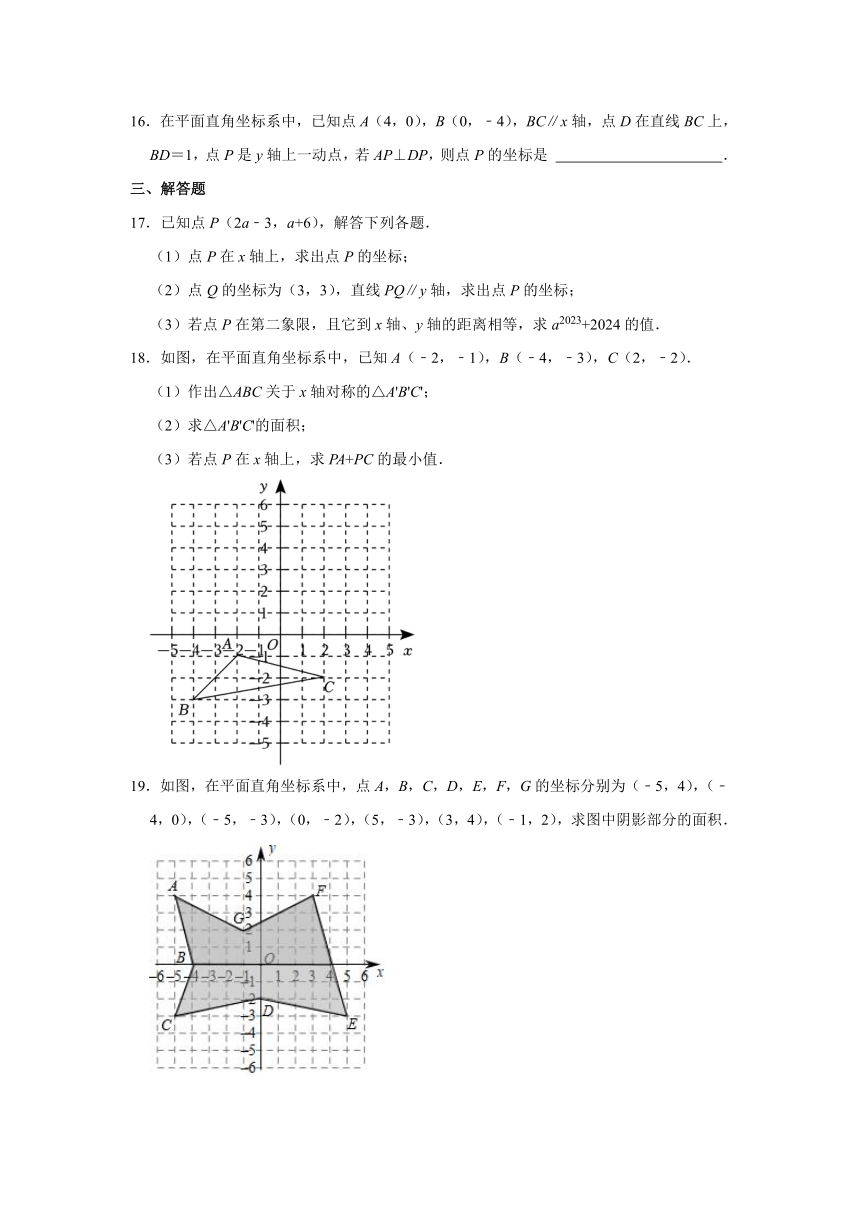
12.已知点P(2m+4,m﹣1)在第一象限,到x轴的距离为2,则m= .
13.如图,将26个英文字母按照如图所示的方式排列,若字母Z用数对(5,4)表示,则数对(4,3)对应的英文字母是 .
14.已知点P(m,n)在第一象限,它到x轴的距离为2,到y轴的距离为3,则点P的坐标是 .
15.在平面直角坐标系中,△ABC和长方形BDOC按如图所示方式放置,已知BC=6,OC=4,AB=AC=5,则点A的坐标为 .
16.在平面直角坐标系中,已知点A(4,0),B(0,﹣4),BC∥x轴,点D在直线BC上,BD=1,点P是y轴上一动点,若AP⊥DP,则点P的坐标是 .
三、解答题
17.已知点P(2a﹣3,a+6),解答下列各题.
(1)点P在x轴上,求出点P的坐标;
(2)点Q的坐标为(3,3),直线PQ∥y轴,求出点P的坐标;
(3)若点P在第二象限,且它到x轴、y轴的距离相等,求a2023+2024的值.
18.如图,在平面直角坐标系中,已知A(﹣2,﹣1),B(﹣4,﹣3),C(2,﹣2).
(1)作出△ABC关于x轴对称的△A'B'C';
(2)求△A'B'C'的面积;
(3)若点P在x轴上,求PA+PC的最小值.
19.如图,在平面直角坐标系中,点A,B,C,D,E,F,G的坐标分别为(﹣5,4),(﹣4,0),(﹣5,﹣3),(0,﹣2),(5,﹣3),(3,4),(﹣1,2),求图中阴影部分的面积.
20.如图,在平面直角坐标系中,△BOC的面积为4,OC=2OB,点A的坐标为(﹣1,4).
(1)写出点B,C的坐标;
(2)计算△ABC的面积.
21.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B,C的坐标分别为(﹣5,5),(﹣3,1)(﹣1,3).
(1)请在如图所示的平面直角坐标系中作出△ABC;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)计算出AB′的长度.
22.如图,在平面直角坐标系中,长方形OABC的边OC,OA分别与x轴,y轴重合,已知点A(0,a),C(b,0),且a,b满足关系式|8﹣a|+(b+6)2=0,若动点P从点A出发,沿着A﹣B﹣C的方向以每秒2个单位长度的速度运动到点C,设点P的运动时间为t.
(1)点B的坐标为 ;
(2)用含t的代数式表示线段BP的长;
(3)若点D的坐标为(0,2),则在点P的运动过程中,是否存在某一时刻使得S△BPDS长方形ABCO,若存在,求出t的值;若不存在,请说明理由.
23.如图是某植物园的平面示意图,在单位长度为1的网格中建立平面直角坐标系,使得沙生植物园的坐标为(﹣1,4),樱花苑的坐标为(﹣3,2).请在图中画出平面直角坐标系;并写出四季花园,杜鹃园,芳香园,澳洲植物区的坐标.
参考答案
一、选择题
1.解:∵点P(2,﹣3),点P与点P′关于y轴对称,
∴P′的坐标为(﹣2,﹣3),
故选:A.
2.解:在平面直角坐标系中,点(0,﹣2)在y轴上.
故选:B.
3.解:∵P(a,b)在第三象限,
∴a<0,b<0,
∴a+b<0,ab>0,
∴点Q(a+b,ab)在第二象限.
故选:B.
4.解:点P(﹣1,3)关于x轴对称的点的坐标是(﹣1,﹣3),
故选:A.
5.解:∵点A(m+1,3m﹣7)在第一、三象限的角平分线上,
∴m+1=3m﹣7,
解得:m=4.
故选:B.
6.解:∵点A(1,﹣2)与点B(a,b)关于直线l对称,
∴a=﹣1﹣[1﹣(﹣1)]=﹣3,b=﹣2,
∴a﹣b=﹣3+2=﹣1.
故选:B.
7.解:由题意得:
m+1=4﹣2m,
m+2m=4﹣1,
3m=3,
m=1,
当m=1时,m+1=2,4﹣2m=2,
∴点P的坐标为(2,2),
故选:A.
8.解:∵点A的坐标为(﹣4,0),点B的坐标为(0,b),
∴OA=4,OB=|b|,
又∵直线AB与两坐标轴围成的三角形的面积为6,
∴OA OB=6,即4 |b|=6,
∴b=±3,
∴b的值为3或﹣3.
故选:D.
9.解:如图,
在坐标系中找到(﹣2,2),(1,2),(1,﹣2)三点,
根据矩形的性质可知,第四个顶点为:(﹣2,﹣2).
故选:D.
10.解:∵A1(1,2),A2(2,1),A3(3,3),A4(4,2),A5(5,4),A6(6,3),…,
观察可得规律:当n是偶数时,An(n,n),
∴A400(400,200),
故选:B.
11.解:∵点B的坐标为(0,5),
∴OB=5,
在Rt△OAB中,
AB12,
∴点A的坐标为(﹣12,5),
故选:B.
二、填空题
12.解:∵点P(2m+4,m﹣1)在第一象限,且到x轴的距离是2,
∴m﹣1=2,
解得:m=3,
故答案为:3.
13.解:∵字母Z用数对(5,4)表示,
∴数对(4,3)对应的英文字母是R,
故答案为:R.
14.解:∵点P在第一象限,且到x轴的距离为2,到y轴的距离为3,
∴点P的横坐标为3,纵坐标为2,
∴点P的坐标是(3,2).
故答案为:(3,2).
15.解:过点A作AE⊥BC于E,交OD于F,如图所示:
∵四边形BDOC是长方形,
∴BC∥DO,BC=DO,∠DOC=∠BCO=90°,
∴AE⊥OD,
∴四边形EFOC是矩形,
∴CE=OF,EF=OC=4,
∵AB=AC,
∴BE=CE=OFBC=3,
在Rt△AEB中,由勾股定理得:AE4,
∴AF=AE+EF=4+4=8,
∴A(﹣3,8),
故答案为:(﹣3,8).
16.解:∵B点的坐标为B(0,﹣4),BC∥x轴,
∴点C的纵坐标为﹣4,
∵点D在直线BC上,BD=1,
∴D1(1,﹣4),D2(﹣1,﹣4),
设点P(0,y),则AP,
如图1,
当点D在D1处时,AD,DP,
∵AP⊥DP,
∴∠APD=90°,
∴AD2=AP2+DP2,即41=16+y2+1+(y+4)2,
解得:y=﹣2+2或y=﹣2﹣2,
∴P1(0,﹣2+2)或P2(0,﹣2﹣2);
如图2,当点D在D2处时,AD=5,DP,
∵AP⊥DP,
∴∠APD=90°,
∴AD2=AP2+DP2,
即25=16+y2+1+(y+4)2,
解得:y=﹣2,
∴P3(0,﹣2);
综上所述:点P的坐标为(0,﹣2+2)或(0,﹣2﹣2)或(0,﹣2),
故答案为:(0,﹣2+2)或(0,﹣2﹣2)或(0,﹣2).
三、解答题
17.解:(1)∵点P(2a﹣3,a+6)在x轴上,
∴a+6=0,
解得:a=﹣6,
∴2a﹣3=2×(﹣6)﹣3=﹣15,
∴点P的坐标(﹣15,0);
(2)∵点Q的坐标为(3,3),直线PQ∥y轴,
∴2a﹣3=3,
解得:a=3,
∴a+6=3+6=9,
∴点P的坐标为(3,9);
(3)∵点P在第二象限,且它到x轴、y轴的距离相等,
∴3﹣2a=a+6,
解得:a=﹣1,
∴a2023+2024=(﹣1)2023+2024=﹣1+2024=2023.
18.解:(1)如图,△A'B'C'即为所求;
(2)△A'B'C'的面积为;
(3)如图,连接A'C,与x轴的交点即为所求的点P,
∴PA+PC的最小值即为A'C的长,
由勾股定理得,
∴PA+PC的最小值为5.
19.解:阴影部分(多边形ABCDEFG)的面积为:
[5﹣(﹣5)]×[4﹣(﹣3)]﹣[4﹣(﹣3)]×1÷2﹣[3﹣(﹣5)]×2÷2﹣2×[4﹣(﹣3)]÷2﹣[5﹣(﹣5)]×1÷2
=10×7﹣3.5﹣8﹣7﹣5
=70﹣23.5
=46.5.
∴阴影部分(多边形ABCDEFG)的面积为46.5.
20.解:(1)设OB=x,则OC=2x,
S△BOCOB×OC4,
∴x=2,
∴OB=2,OC=4,
∴B点坐标为(0,2),C点坐标(4,0).
(2)如图,过A点作AD⊥DC,
由题意可知,
OD=1,AD=4,CD=4+1=5,
四边形ADOB为梯形,
∴S梯形ADOB3,
∴S△ADCAD×CD4×5=10,
∴S△ABC=S△ADC﹣S梯形ADOB﹣S△BOC=10﹣3﹣4=3.
∴S△ABC=3.
21.解:(1)如图,△ABC即为所求;
(2)如图,△A′B′C′即为所求;
(3)AB′4.
22.解:(1)∵|8﹣a|+(b+6)2=0,
又∵|8﹣a|≥0,(b+6)2≥0,
∴a=8,b=﹣6,
∴A(0,8),C(﹣6,0),
∵四边形ABCO是矩形,
∴B(﹣6,8);
故答案为:(﹣6,8);
(2)当0≤t<3时,PB=6﹣2t,
当3≤t≤7时,PB=2t﹣6;
(3)如图,当点P在线段AB上时,(6﹣2t)×66×8,
∴t=1.
当点P在线段BC上时,(2t﹣6)×66×8,
∴t=5.
综上所述,满足条件的t的值为1或5.
23.解:建立直角坐标系如图,
四季花园(2,﹣2),杜鹃园(2,3),芳香园(1,1),澳洲植物区(﹣2,﹣2).
一、选择题
1.已知点P(2,﹣3),则点P关于y轴对称点P′的坐标为( )
A.(﹣2,﹣3) B.(﹣2,3) C.(2,﹣3) D.(2,3)
2.在平面直角坐标系中,点(0,﹣2)在( )
A.x轴上 B.y轴上 C.第三象限 D.第四象限
3.如果P(a,b)在第三象限,那么点Q(a+b,ab)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.点P(﹣1,3)关于x轴对称的点的坐标是( )
A.(﹣1,﹣3) B.(1,﹣3) C.(1,3) D.(﹣3,1)
5.点A(m+1,3m﹣7)在第一、三象限的角平分线上,则m的值为( )
A.3 B.4 C.5 D.6
6.如图,点A(1,﹣2)与点B(a,b)关于直线l对称,则a﹣b的值为( )
A.1 B.﹣1 C.2 D.﹣5
7.若点P(m+1,4﹣2m)在第一、三象限的平分线上,则点P的坐标为( )
A.(2,2) B.(6,﹣6) C.(﹣2,﹣2) D.(6,6)
8.已知A(﹣4,0)和B(0,b)两点,若直线AB与两坐标轴围成的三角形的面积为6,则b的值为( )
A.6 B.6或﹣6 C.3 D.3或﹣3
9.在平面直角坐标系中有一个长方形,其中三个顶点的坐标分别为(﹣2,2),(1,2),(1,﹣2),则第四个顶点的坐标为( )
A.(﹣1,2) B.(1,﹣1) C.(2,﹣2) D.(﹣2,﹣2)
10.如图,在平面直角坐标系中,已知A1(1,2),A2(2,1),A3(3,3),A4(4,2),A5(5,4),A6(6,3),…,以此类推,A400的坐标为( )
A.(200,100) B.(400,200) C.(400,400) D.(400,800)
11.在平面直角坐标系中,Rt△OAB的位置如图所示,其中∠ABO=90°,若点B的坐标为(0,5),OA=13,则点A的坐标为( )
A.(﹣13,5) B.(﹣12,5) C.(﹣7,5) D.(1 2,5)
二、填空题
12.已知点P(2m+4,m﹣1)在第一象限,到x轴的距离为2,则m= .
13.如图,将26个英文字母按照如图所示的方式排列,若字母Z用数对(5,4)表示,则数对(4,3)对应的英文字母是 .
14.已知点P(m,n)在第一象限,它到x轴的距离为2,到y轴的距离为3,则点P的坐标是 .
15.在平面直角坐标系中,△ABC和长方形BDOC按如图所示方式放置,已知BC=6,OC=4,AB=AC=5,则点A的坐标为 .
16.在平面直角坐标系中,已知点A(4,0),B(0,﹣4),BC∥x轴,点D在直线BC上,BD=1,点P是y轴上一动点,若AP⊥DP,则点P的坐标是 .
三、解答题
17.已知点P(2a﹣3,a+6),解答下列各题.
(1)点P在x轴上,求出点P的坐标;
(2)点Q的坐标为(3,3),直线PQ∥y轴,求出点P的坐标;
(3)若点P在第二象限,且它到x轴、y轴的距离相等,求a2023+2024的值.
18.如图,在平面直角坐标系中,已知A(﹣2,﹣1),B(﹣4,﹣3),C(2,﹣2).
(1)作出△ABC关于x轴对称的△A'B'C';
(2)求△A'B'C'的面积;
(3)若点P在x轴上,求PA+PC的最小值.
19.如图,在平面直角坐标系中,点A,B,C,D,E,F,G的坐标分别为(﹣5,4),(﹣4,0),(﹣5,﹣3),(0,﹣2),(5,﹣3),(3,4),(﹣1,2),求图中阴影部分的面积.
20.如图,在平面直角坐标系中,△BOC的面积为4,OC=2OB,点A的坐标为(﹣1,4).
(1)写出点B,C的坐标;
(2)计算△ABC的面积.
21.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B,C的坐标分别为(﹣5,5),(﹣3,1)(﹣1,3).
(1)请在如图所示的平面直角坐标系中作出△ABC;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)计算出AB′的长度.
22.如图,在平面直角坐标系中,长方形OABC的边OC,OA分别与x轴,y轴重合,已知点A(0,a),C(b,0),且a,b满足关系式|8﹣a|+(b+6)2=0,若动点P从点A出发,沿着A﹣B﹣C的方向以每秒2个单位长度的速度运动到点C,设点P的运动时间为t.
(1)点B的坐标为 ;
(2)用含t的代数式表示线段BP的长;
(3)若点D的坐标为(0,2),则在点P的运动过程中,是否存在某一时刻使得S△BPDS长方形ABCO,若存在,求出t的值;若不存在,请说明理由.
23.如图是某植物园的平面示意图,在单位长度为1的网格中建立平面直角坐标系,使得沙生植物园的坐标为(﹣1,4),樱花苑的坐标为(﹣3,2).请在图中画出平面直角坐标系;并写出四季花园,杜鹃园,芳香园,澳洲植物区的坐标.
参考答案
一、选择题
1.解:∵点P(2,﹣3),点P与点P′关于y轴对称,
∴P′的坐标为(﹣2,﹣3),
故选:A.
2.解:在平面直角坐标系中,点(0,﹣2)在y轴上.
故选:B.
3.解:∵P(a,b)在第三象限,
∴a<0,b<0,
∴a+b<0,ab>0,
∴点Q(a+b,ab)在第二象限.
故选:B.
4.解:点P(﹣1,3)关于x轴对称的点的坐标是(﹣1,﹣3),
故选:A.
5.解:∵点A(m+1,3m﹣7)在第一、三象限的角平分线上,
∴m+1=3m﹣7,
解得:m=4.
故选:B.
6.解:∵点A(1,﹣2)与点B(a,b)关于直线l对称,
∴a=﹣1﹣[1﹣(﹣1)]=﹣3,b=﹣2,
∴a﹣b=﹣3+2=﹣1.
故选:B.
7.解:由题意得:
m+1=4﹣2m,
m+2m=4﹣1,
3m=3,
m=1,
当m=1时,m+1=2,4﹣2m=2,
∴点P的坐标为(2,2),
故选:A.
8.解:∵点A的坐标为(﹣4,0),点B的坐标为(0,b),
∴OA=4,OB=|b|,
又∵直线AB与两坐标轴围成的三角形的面积为6,
∴OA OB=6,即4 |b|=6,
∴b=±3,
∴b的值为3或﹣3.
故选:D.
9.解:如图,
在坐标系中找到(﹣2,2),(1,2),(1,﹣2)三点,
根据矩形的性质可知,第四个顶点为:(﹣2,﹣2).
故选:D.
10.解:∵A1(1,2),A2(2,1),A3(3,3),A4(4,2),A5(5,4),A6(6,3),…,
观察可得规律:当n是偶数时,An(n,n),
∴A400(400,200),
故选:B.
11.解:∵点B的坐标为(0,5),
∴OB=5,
在Rt△OAB中,
AB12,
∴点A的坐标为(﹣12,5),
故选:B.
二、填空题
12.解:∵点P(2m+4,m﹣1)在第一象限,且到x轴的距离是2,
∴m﹣1=2,
解得:m=3,
故答案为:3.
13.解:∵字母Z用数对(5,4)表示,
∴数对(4,3)对应的英文字母是R,
故答案为:R.
14.解:∵点P在第一象限,且到x轴的距离为2,到y轴的距离为3,
∴点P的横坐标为3,纵坐标为2,
∴点P的坐标是(3,2).
故答案为:(3,2).
15.解:过点A作AE⊥BC于E,交OD于F,如图所示:
∵四边形BDOC是长方形,
∴BC∥DO,BC=DO,∠DOC=∠BCO=90°,
∴AE⊥OD,
∴四边形EFOC是矩形,
∴CE=OF,EF=OC=4,
∵AB=AC,
∴BE=CE=OFBC=3,
在Rt△AEB中,由勾股定理得:AE4,
∴AF=AE+EF=4+4=8,
∴A(﹣3,8),
故答案为:(﹣3,8).
16.解:∵B点的坐标为B(0,﹣4),BC∥x轴,
∴点C的纵坐标为﹣4,
∵点D在直线BC上,BD=1,
∴D1(1,﹣4),D2(﹣1,﹣4),
设点P(0,y),则AP,
如图1,
当点D在D1处时,AD,DP,
∵AP⊥DP,
∴∠APD=90°,
∴AD2=AP2+DP2,即41=16+y2+1+(y+4)2,
解得:y=﹣2+2或y=﹣2﹣2,
∴P1(0,﹣2+2)或P2(0,﹣2﹣2);
如图2,当点D在D2处时,AD=5,DP,
∵AP⊥DP,
∴∠APD=90°,
∴AD2=AP2+DP2,
即25=16+y2+1+(y+4)2,
解得:y=﹣2,
∴P3(0,﹣2);
综上所述:点P的坐标为(0,﹣2+2)或(0,﹣2﹣2)或(0,﹣2),
故答案为:(0,﹣2+2)或(0,﹣2﹣2)或(0,﹣2).
三、解答题
17.解:(1)∵点P(2a﹣3,a+6)在x轴上,
∴a+6=0,
解得:a=﹣6,
∴2a﹣3=2×(﹣6)﹣3=﹣15,
∴点P的坐标(﹣15,0);
(2)∵点Q的坐标为(3,3),直线PQ∥y轴,
∴2a﹣3=3,
解得:a=3,
∴a+6=3+6=9,
∴点P的坐标为(3,9);
(3)∵点P在第二象限,且它到x轴、y轴的距离相等,
∴3﹣2a=a+6,
解得:a=﹣1,
∴a2023+2024=(﹣1)2023+2024=﹣1+2024=2023.
18.解:(1)如图,△A'B'C'即为所求;
(2)△A'B'C'的面积为;
(3)如图,连接A'C,与x轴的交点即为所求的点P,
∴PA+PC的最小值即为A'C的长,
由勾股定理得,
∴PA+PC的最小值为5.
19.解:阴影部分(多边形ABCDEFG)的面积为:
[5﹣(﹣5)]×[4﹣(﹣3)]﹣[4﹣(﹣3)]×1÷2﹣[3﹣(﹣5)]×2÷2﹣2×[4﹣(﹣3)]÷2﹣[5﹣(﹣5)]×1÷2
=10×7﹣3.5﹣8﹣7﹣5
=70﹣23.5
=46.5.
∴阴影部分(多边形ABCDEFG)的面积为46.5.
20.解:(1)设OB=x,则OC=2x,
S△BOCOB×OC4,
∴x=2,
∴OB=2,OC=4,
∴B点坐标为(0,2),C点坐标(4,0).
(2)如图,过A点作AD⊥DC,
由题意可知,
OD=1,AD=4,CD=4+1=5,
四边形ADOB为梯形,
∴S梯形ADOB3,
∴S△ADCAD×CD4×5=10,
∴S△ABC=S△ADC﹣S梯形ADOB﹣S△BOC=10﹣3﹣4=3.
∴S△ABC=3.
21.解:(1)如图,△ABC即为所求;
(2)如图,△A′B′C′即为所求;
(3)AB′4.
22.解:(1)∵|8﹣a|+(b+6)2=0,
又∵|8﹣a|≥0,(b+6)2≥0,
∴a=8,b=﹣6,
∴A(0,8),C(﹣6,0),
∵四边形ABCO是矩形,
∴B(﹣6,8);
故答案为:(﹣6,8);
(2)当0≤t<3时,PB=6﹣2t,
当3≤t≤7时,PB=2t﹣6;
(3)如图,当点P在线段AB上时,(6﹣2t)×66×8,
∴t=1.
当点P在线段BC上时,(2t﹣6)×66×8,
∴t=5.
综上所述,满足条件的t的值为1或5.
23.解:建立直角坐标系如图,
四季花园(2,﹣2),杜鹃园(2,3),芳香园(1,1),澳洲植物区(﹣2,﹣2).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
