第1章勾股定理培优训练(无答案)2023-2024学年北师大版数学八年级上册
文档属性
| 名称 | 第1章勾股定理培优训练(无答案)2023-2024学年北师大版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 181.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-07 15:00:47 | ||
图片预览

文档简介
第1章勾股定理培优训练2023-2024年度北师大版八上册
一.选择题
1.在直角三角形中,若勾为3,股为4,则弦为( )
A.5 B.6 C.7 D.8
2.下列各组数为勾股数的是( )
A.1,1, B.4,5,6 C.8,9,10 D.5,12,13
3.在△ABC中,AB=1,AC=2,BC=,则该三角形为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
4.一根高9m的旗杆在离地4m高处折断,折断处仍相连,此时在3.9m远处耍的身高为1m的小明( )
A.没有危险 B.有危险 C.可能有危险 D.无法判断
5.如图,以数轴原点为中心,将边长为 的正方形的对角线 ,逆时针旋转 落到数轴的 处,则点 表示的数是
A. B. C. D.
6.如图,将一根长为16cm的橡皮筋固定在笔直的木棒上,两端点分别记为A,B,然后将中点C向上竖直拉升6cm至点D处,则拉伸后橡皮筋的长为( )
A.20cm B.22cm C.28cm D.32cm
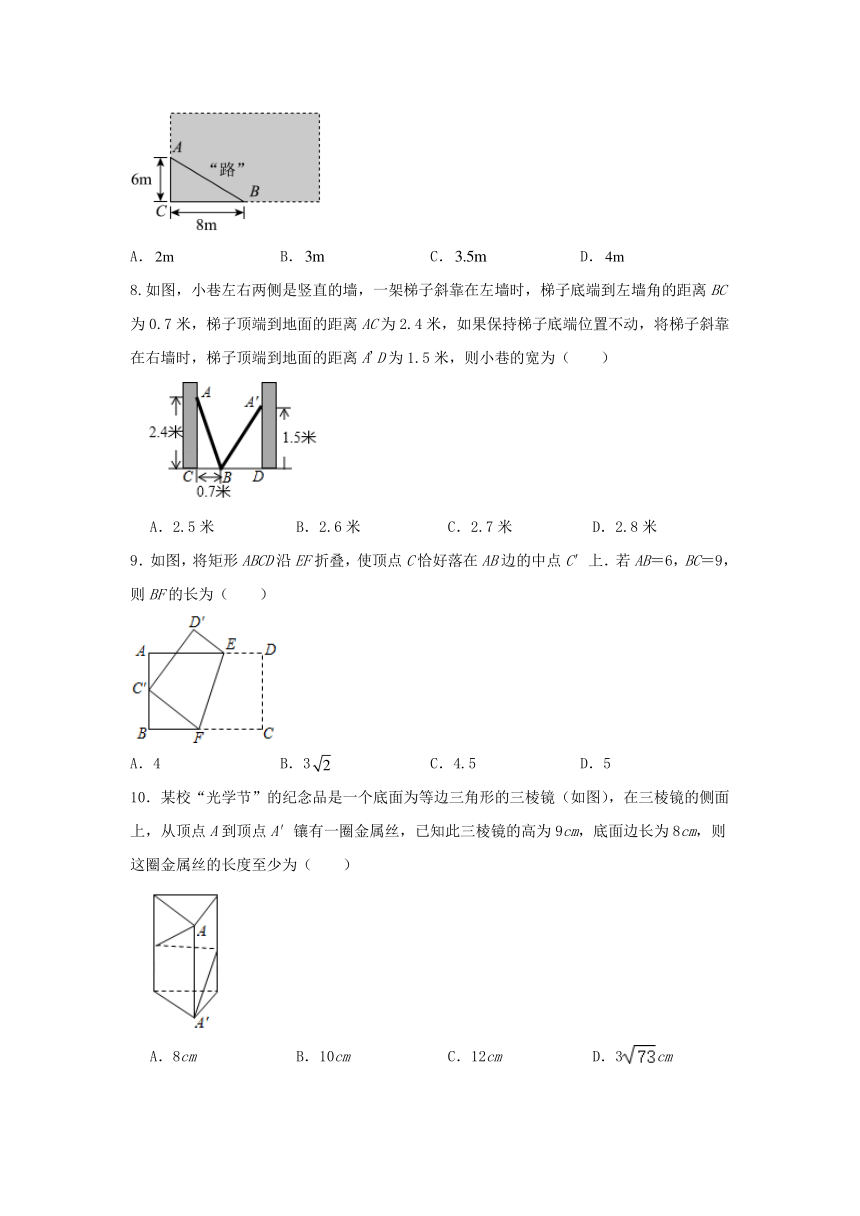
7.如图,某小区有一块长方形花圃,为了方便居民不用再走拐角,打算用瓷砖铺上一条新路,居民走新路比走拐角近( )
A. B. C. D.
8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5米,则小巷的宽为( )
A.2.5米 B.2.6米 C.2.7米 D.2.8米
9.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A.4 B.3 C.4.5 D.5
10.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图),在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为8cm,则这圈金属丝的长度至少为( )
A.8cm B.10cm C.12cm D.3cm
二.填空题
11.一直角三角形的斜边长比一直角边大 ,另一直角边长为 ,则斜边长为 .
12.若ABC的三边分别是a.b.c,且a.b.c满足a2+c2=b2,则∠ =90 o
13.学校有一块长方形的花圃如右图所示,有少数的同学为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了________步(假设1米=2步),却踩伤了花草,所谓“花草无辜,踩之何忍”!
14.古算趣题:“笨人执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭.有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足.借问竿长多少数,谁人算出我佩服.”若设竿长为x尺,则可列方程为__________.
15.如图,长方体的长,宽,高分别是6,3,5,现一只蚂蚁从A点爬行到B点,设爬行的最短路线长为d,则d2的值是 .
16.如图是第七届国际数学教育大会的会徽图案,它是由一串有公共顶点O的直角三角形组成的,图中的OA1=A1A2=A2A3=…=A7A8=1,按此规律,在线段OA1,OA2,OA3,…,OA10中,长度为整数的线段有 条.
三.解答题
17.如图,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,请按要求完成下列各题:
(1)作线段,使其长度为;
(2)通过计算说明是直角三角形.
18.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=100m,AC=60m,求A,B两点间的距离.
19.如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?
20.自2022年以来,安宁市建起了多个“口袋公园”,它们既美化了城市空间,又拓展了市民的公共活动场所,还体现着城市风貌和文化.如图,在某小区旁有一块四边形空地,其中∠B=90°,AB=20m,BC=15m,AD=24m,CD=7m.
(1)如图,连接AC,试求AC的长;
(2)安宁市委、市政府计划将其打造为“口袋公园”,经测算,每平方米的费用为2000元,请你计算将这块地打造成“口袋公园”需要多少钱.
21.现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,已知消防车高,云梯最多只能伸长到,救人时云梯伸至最长如图,云梯先在处完成从高处救人后,然后前进到处从高处救人.
(1)_________米,_________米;
(2)①求消防车在处离楼房的距离(的长度);
②求消防车两次救援移动的距离(的长度).(精确到,参考数据,,)
一.选择题
1.在直角三角形中,若勾为3,股为4,则弦为( )
A.5 B.6 C.7 D.8
2.下列各组数为勾股数的是( )
A.1,1, B.4,5,6 C.8,9,10 D.5,12,13
3.在△ABC中,AB=1,AC=2,BC=,则该三角形为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
4.一根高9m的旗杆在离地4m高处折断,折断处仍相连,此时在3.9m远处耍的身高为1m的小明( )
A.没有危险 B.有危险 C.可能有危险 D.无法判断
5.如图,以数轴原点为中心,将边长为 的正方形的对角线 ,逆时针旋转 落到数轴的 处,则点 表示的数是
A. B. C. D.
6.如图,将一根长为16cm的橡皮筋固定在笔直的木棒上,两端点分别记为A,B,然后将中点C向上竖直拉升6cm至点D处,则拉伸后橡皮筋的长为( )
A.20cm B.22cm C.28cm D.32cm
7.如图,某小区有一块长方形花圃,为了方便居民不用再走拐角,打算用瓷砖铺上一条新路,居民走新路比走拐角近( )
A. B. C. D.
8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5米,则小巷的宽为( )
A.2.5米 B.2.6米 C.2.7米 D.2.8米
9.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A.4 B.3 C.4.5 D.5
10.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图),在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为8cm,则这圈金属丝的长度至少为( )
A.8cm B.10cm C.12cm D.3cm
二.填空题
11.一直角三角形的斜边长比一直角边大 ,另一直角边长为 ,则斜边长为 .
12.若ABC的三边分别是a.b.c,且a.b.c满足a2+c2=b2,则∠ =90 o
13.学校有一块长方形的花圃如右图所示,有少数的同学为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了________步(假设1米=2步),却踩伤了花草,所谓“花草无辜,踩之何忍”!
14.古算趣题:“笨人执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭.有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足.借问竿长多少数,谁人算出我佩服.”若设竿长为x尺,则可列方程为__________.
15.如图,长方体的长,宽,高分别是6,3,5,现一只蚂蚁从A点爬行到B点,设爬行的最短路线长为d,则d2的值是 .
16.如图是第七届国际数学教育大会的会徽图案,它是由一串有公共顶点O的直角三角形组成的,图中的OA1=A1A2=A2A3=…=A7A8=1,按此规律,在线段OA1,OA2,OA3,…,OA10中,长度为整数的线段有 条.
三.解答题
17.如图,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,请按要求完成下列各题:
(1)作线段,使其长度为;
(2)通过计算说明是直角三角形.
18.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=100m,AC=60m,求A,B两点间的距离.
19.如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?
20.自2022年以来,安宁市建起了多个“口袋公园”,它们既美化了城市空间,又拓展了市民的公共活动场所,还体现着城市风貌和文化.如图,在某小区旁有一块四边形空地,其中∠B=90°,AB=20m,BC=15m,AD=24m,CD=7m.
(1)如图,连接AC,试求AC的长;
(2)安宁市委、市政府计划将其打造为“口袋公园”,经测算,每平方米的费用为2000元,请你计算将这块地打造成“口袋公园”需要多少钱.
21.现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,已知消防车高,云梯最多只能伸长到,救人时云梯伸至最长如图,云梯先在处完成从高处救人后,然后前进到处从高处救人.
(1)_________米,_________米;
(2)①求消防车在处离楼房的距离(的长度);
②求消防车两次救援移动的距离(的长度).(精确到,参考数据,,)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
