13.2 画轴对称图形基础巩固卷2023--2024学年人教版八年级数学上册(含答案)
文档属性
| 名称 | 13.2 画轴对称图形基础巩固卷2023--2024学年人教版八年级数学上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 158.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-07 15:55:46 | ||
图片预览



文档简介
2023年人教版数学八年级上册
《13.2 画轴对称图形》基础巩固卷
一 、选择题
1.下列说法正确的是( )
A.两个全等的三角形一定关于某条直线对称
B.关于某条直线的对称的两个三角形一定全等
C.直角三角形是轴对称图形
D.锐角三角形都是轴对称图形
2.如图,△ABC与△DEF关于直线MN对称,则以下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.A,D两点所连的线段被MN垂直平分
3.两个图形关于某直线对称,对称点一定( )
A.这直线的两旁 B.这直线的同旁 C.这直线上 D.这直线两旁或这直线上
4.已知互不平行的两条线段AB,CD关于直线l对称,AB,CD所在直线交于点P.
下列结论中:①AB=CD;
②点P在直线l上;
③若A、C是对称点,则l垂直平分线段AC;
④若B、D是对称点,则PB=PD.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
5.对于下列命题:
①关于某一直线成轴对称的两个三角形全等;
②等腰三角形的对称轴是顶角的平分线;
③一条线段的两个端点一定是关于经过该线段中点的直线的对称点;
④如果两个三角形全等,那么它们关于某直线成轴对称.
其中真命题的个数为( )
A.0 B.1 C.2 D.3
6.如图△ABC和△A'B'C'关于直线l对称.
下列结论中:
①△ABC△A'B'C';
②∠BAC'=∠B'AC;
③l垂直平分CC';
④直线BC和B'C',的交点不一定在l上.
正确的有( )
A.4个 B.3个 C.2个 D.1个
7.下列命题中,正确的是( )
A.两个全等的三角形合在一起是一个轴对称图形
B.等腰三角形的对称轴是底边上的中线
C.等腰三角形底边上的高就是底边的垂直平分线
D.一条线段可以看做以它的垂直平分线为对称轴的轴对称图形
8.已知点A(3x﹣6,4y+15),点B(5y,x)关于x轴对称,则x+y值是( )
A.0 B.9 C.﹣6 D.﹣12
9.已知两点的坐标分别是(﹣2,3)和(2,3),则下列情况正确的有( )
①两点关于x轴对称
②两点关于y轴对称
③两点之间距离为4.
A.3个 B.2个 C.1个 D.0个
10.如图,由4个小正方形组成的田字格,△ABC的顶点都是小正方形的顶点,在田字格上能画出与△ABC成轴对称,且顶点都在小正方形顶点上的三角形的个数共有( )
A.2个 B.3个 C.4个 D.5个
二 、填空题
11.点M(3,﹣4)关于x轴的对称点的坐标是 .
12.成轴对称的两个图形 .
13.如图,Rt△AFC和Rt△AEB关于虚线成轴对称,现给出下列结论:
①∠1=∠2;②△ANC≌△AMB;③CD=DN.
其中正确的结论是 .(填序号)
14.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为 .
15.点(a+2b,3a-3)和点(-2a-b-1,2a-b)关于y轴对称,则a= ,b= .
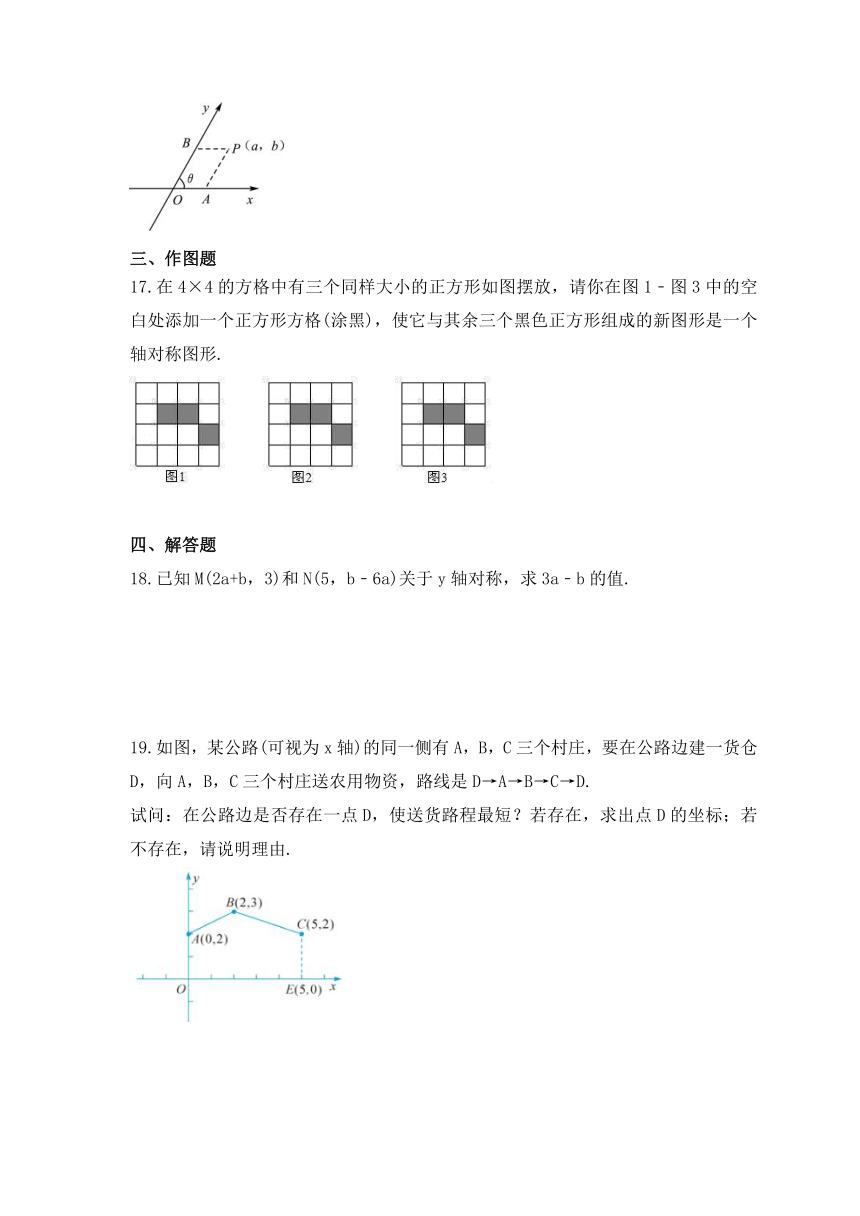
16.如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B.若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标.在某平面斜坐标系中,已知θ=60°,点M的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为________________.
三 、作图题
17.在4×4的方格中有三个同样大小的正方形如图摆放,请你在图1﹣图3中的空白处添加一个正方形方格(涂黑),使它与其余三个黑色正方形组成的新图形是一个轴对称图形.
四 、解答题
18.已知M(2a+b,3)和N(5,b﹣6a)关于y轴对称,求3a﹣b的值.
19.如图,某公路(可视为x轴)的同一侧有A,B,C三个村庄,要在公路边建一货仓D,向A,B,C三个村庄送农用物资,路线是D→A→B→C→D.
试问:在公路边是否存在一点D,使送货路程最短?若存在,求出点D的坐标;若不存在,请说明理由.
20.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
21.如图,AD平分∠BAC,EF垂直平分AD交BC的延长线于F,连接AF.
求证:∠B=∠CAF.
22.如图,把△ABC沿DE折叠,使点A落在四边形BCDE内部的点A'处.
(1)写出图中一对全等的三角形,并写出它们的所有对应角.
(2)设∠AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少(用含有x或y的式子表示)
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.
23.在平面直角坐标系中,直线1垂直于x轴,垂足为M(m,0),点A(﹣1,0)关于直线的对称点为A′.
探究:
(1)当m=0时,A′的坐标为 ;
(2)当m=1时,A′的坐标为 ;
(3)当m=2时,A′的坐标为 ;
发现:对于任意的m,A′的坐标为 .
解决问题:
若A(﹣1,0)B(﹣5,0),C(6,0),D(15,0),将线段AB沿直线l翻折得到线段A′B′,若线段A′B′与线段CD重合部分的长为2,求m的值.
答案
1.B
2.A
3.D
4.D
5.B
6.B
7.D
8.C
9.B
10.C.
11.答案为:(3,4).
12.答案为:全等.
13.答案为:①②.
14.答案为:8 cm2.
15.答案为:1,2
16.答案为:(﹣3,5).
17.解:如图所示:
.
18.解:∵M(2a+b,3)和N(5,b﹣6a)关于y轴对称,
∴2a+b=﹣5,b﹣6a=3,
解得a=﹣1,b=﹣3,
∴3a﹣b=3×(﹣1)﹣(﹣3)=﹣3+3=0.
19.解:存在.
∵路程即为DA+AB+BC+DC,AB+BC的长度固定,
∴要使路程最短,只需DA+DC最短即可.
作点A关于x轴的对称点A′(0,-2),连结A′C,则A′C与x轴的交点即为点D.
过点C作CE⊥x轴于点E,则点E(5,0).
易得△OA′D≌△ECD,得OD=ED,
∴点D(,0).
20.解:(1)∵∠BAC=50°,AD平分∠BAC,
∴∠EAD=∠BAC=25°,
∵DE⊥AB,
∴∠AED=90°,
∴∠EDA=90°﹣25°=65°.
(2)证明:∵DE⊥AB,
∴∠AED=90°=∠ACB,
又∵AD平分∠BAC,
∴∠DAE=∠DAC,
∵AD=AD,
∴△AED≌△ACD,
∴AE=AC,
∵AD平分∠BAC,
∴AD⊥CE,
即直线AD是线段CE的垂直平分线.
21.证明:∵EF垂直平分AD,
∴AF=DF,∠ADF=∠DAF,
∵∠ADF=∠B+∠BAD,∠DAF=∠CAF+∠CAD,
又∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠B=∠CAF.
22.解:(1)△EAD≌△EA'D,其中∠EAD=∠EA'D,
∠AED=∠A'ED,∠ADE=∠A'DE.
(2)∠1=180°-2x,∠2=180°-2y.
(3)∠1+∠2=360°-2(x+y)=360°-2(180°-∠A)=2∠A.
规律为∠1+∠2=2∠A.
23.解:探究:∵点A和A′关于直线l对称,
∴M为线段AA′的中点,
设A′坐标为(t,0),且M(m,0),A(﹣1,0),
∴AM=A′M,即m﹣(﹣1)=t﹣m,
∴t=2m+1,
(1)当m=0时,t=1,则A'的坐标为 (1,0),故答案为:(1,0);
(2)当m=1时,t=2×1+1=3,则A'的坐标为(3,0),故答案为:(3,0);
(3)当m=2时,t=2×2+1=5,则A'的坐标为(5,0),故答案为:(5,0);
发现:由探究可知,对于任意的m,t=2m+1,则A'的坐标为(2m+1,0),
故答案为:(2m+1,0);
解决问题:
∵A(﹣1,0)B(﹣5,0),∴A′(2m+1,0),B′(2m+5,0),
当B′在点C、D之间时,则重合部分为线段CB′,且C(6,0),
∴2m+5﹣6=2,解得m=;
当A′在点C、D之间时,则重合部分为线段A′D,且D(15,0),
∴15﹣(2m+1)=2,解得m=6;
综上可知m的值为或6.
《13.2 画轴对称图形》基础巩固卷
一 、选择题
1.下列说法正确的是( )
A.两个全等的三角形一定关于某条直线对称
B.关于某条直线的对称的两个三角形一定全等
C.直角三角形是轴对称图形
D.锐角三角形都是轴对称图形
2.如图,△ABC与△DEF关于直线MN对称,则以下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.A,D两点所连的线段被MN垂直平分
3.两个图形关于某直线对称,对称点一定( )
A.这直线的两旁 B.这直线的同旁 C.这直线上 D.这直线两旁或这直线上
4.已知互不平行的两条线段AB,CD关于直线l对称,AB,CD所在直线交于点P.
下列结论中:①AB=CD;
②点P在直线l上;
③若A、C是对称点,则l垂直平分线段AC;
④若B、D是对称点,则PB=PD.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
5.对于下列命题:
①关于某一直线成轴对称的两个三角形全等;
②等腰三角形的对称轴是顶角的平分线;
③一条线段的两个端点一定是关于经过该线段中点的直线的对称点;
④如果两个三角形全等,那么它们关于某直线成轴对称.
其中真命题的个数为( )
A.0 B.1 C.2 D.3
6.如图△ABC和△A'B'C'关于直线l对称.
下列结论中:
①△ABC△A'B'C';
②∠BAC'=∠B'AC;
③l垂直平分CC';
④直线BC和B'C',的交点不一定在l上.
正确的有( )
A.4个 B.3个 C.2个 D.1个
7.下列命题中,正确的是( )
A.两个全等的三角形合在一起是一个轴对称图形
B.等腰三角形的对称轴是底边上的中线
C.等腰三角形底边上的高就是底边的垂直平分线
D.一条线段可以看做以它的垂直平分线为对称轴的轴对称图形
8.已知点A(3x﹣6,4y+15),点B(5y,x)关于x轴对称,则x+y值是( )
A.0 B.9 C.﹣6 D.﹣12
9.已知两点的坐标分别是(﹣2,3)和(2,3),则下列情况正确的有( )
①两点关于x轴对称
②两点关于y轴对称
③两点之间距离为4.
A.3个 B.2个 C.1个 D.0个
10.如图,由4个小正方形组成的田字格,△ABC的顶点都是小正方形的顶点,在田字格上能画出与△ABC成轴对称,且顶点都在小正方形顶点上的三角形的个数共有( )
A.2个 B.3个 C.4个 D.5个
二 、填空题
11.点M(3,﹣4)关于x轴的对称点的坐标是 .
12.成轴对称的两个图形 .
13.如图,Rt△AFC和Rt△AEB关于虚线成轴对称,现给出下列结论:
①∠1=∠2;②△ANC≌△AMB;③CD=DN.
其中正确的结论是 .(填序号)
14.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为 .
15.点(a+2b,3a-3)和点(-2a-b-1,2a-b)关于y轴对称,则a= ,b= .
16.如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B.若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标.在某平面斜坐标系中,已知θ=60°,点M的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为________________.
三 、作图题
17.在4×4的方格中有三个同样大小的正方形如图摆放,请你在图1﹣图3中的空白处添加一个正方形方格(涂黑),使它与其余三个黑色正方形组成的新图形是一个轴对称图形.
四 、解答题
18.已知M(2a+b,3)和N(5,b﹣6a)关于y轴对称,求3a﹣b的值.
19.如图,某公路(可视为x轴)的同一侧有A,B,C三个村庄,要在公路边建一货仓D,向A,B,C三个村庄送农用物资,路线是D→A→B→C→D.
试问:在公路边是否存在一点D,使送货路程最短?若存在,求出点D的坐标;若不存在,请说明理由.
20.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度数;
(2)求证:直线AD是线段CE的垂直平分线.
21.如图,AD平分∠BAC,EF垂直平分AD交BC的延长线于F,连接AF.
求证:∠B=∠CAF.
22.如图,把△ABC沿DE折叠,使点A落在四边形BCDE内部的点A'处.
(1)写出图中一对全等的三角形,并写出它们的所有对应角.
(2)设∠AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少(用含有x或y的式子表示)
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.
23.在平面直角坐标系中,直线1垂直于x轴,垂足为M(m,0),点A(﹣1,0)关于直线的对称点为A′.
探究:
(1)当m=0时,A′的坐标为 ;
(2)当m=1时,A′的坐标为 ;
(3)当m=2时,A′的坐标为 ;
发现:对于任意的m,A′的坐标为 .
解决问题:
若A(﹣1,0)B(﹣5,0),C(6,0),D(15,0),将线段AB沿直线l翻折得到线段A′B′,若线段A′B′与线段CD重合部分的长为2,求m的值.
答案
1.B
2.A
3.D
4.D
5.B
6.B
7.D
8.C
9.B
10.C.
11.答案为:(3,4).
12.答案为:全等.
13.答案为:①②.
14.答案为:8 cm2.
15.答案为:1,2
16.答案为:(﹣3,5).
17.解:如图所示:
.
18.解:∵M(2a+b,3)和N(5,b﹣6a)关于y轴对称,
∴2a+b=﹣5,b﹣6a=3,
解得a=﹣1,b=﹣3,
∴3a﹣b=3×(﹣1)﹣(﹣3)=﹣3+3=0.
19.解:存在.
∵路程即为DA+AB+BC+DC,AB+BC的长度固定,
∴要使路程最短,只需DA+DC最短即可.
作点A关于x轴的对称点A′(0,-2),连结A′C,则A′C与x轴的交点即为点D.
过点C作CE⊥x轴于点E,则点E(5,0).
易得△OA′D≌△ECD,得OD=ED,
∴点D(,0).
20.解:(1)∵∠BAC=50°,AD平分∠BAC,
∴∠EAD=∠BAC=25°,
∵DE⊥AB,
∴∠AED=90°,
∴∠EDA=90°﹣25°=65°.
(2)证明:∵DE⊥AB,
∴∠AED=90°=∠ACB,
又∵AD平分∠BAC,
∴∠DAE=∠DAC,
∵AD=AD,
∴△AED≌△ACD,
∴AE=AC,
∵AD平分∠BAC,
∴AD⊥CE,
即直线AD是线段CE的垂直平分线.
21.证明:∵EF垂直平分AD,
∴AF=DF,∠ADF=∠DAF,
∵∠ADF=∠B+∠BAD,∠DAF=∠CAF+∠CAD,
又∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠B=∠CAF.
22.解:(1)△EAD≌△EA'D,其中∠EAD=∠EA'D,
∠AED=∠A'ED,∠ADE=∠A'DE.
(2)∠1=180°-2x,∠2=180°-2y.
(3)∠1+∠2=360°-2(x+y)=360°-2(180°-∠A)=2∠A.
规律为∠1+∠2=2∠A.
23.解:探究:∵点A和A′关于直线l对称,
∴M为线段AA′的中点,
设A′坐标为(t,0),且M(m,0),A(﹣1,0),
∴AM=A′M,即m﹣(﹣1)=t﹣m,
∴t=2m+1,
(1)当m=0时,t=1,则A'的坐标为 (1,0),故答案为:(1,0);
(2)当m=1时,t=2×1+1=3,则A'的坐标为(3,0),故答案为:(3,0);
(3)当m=2时,t=2×2+1=5,则A'的坐标为(5,0),故答案为:(5,0);
发现:由探究可知,对于任意的m,t=2m+1,则A'的坐标为(2m+1,0),
故答案为:(2m+1,0);
解决问题:
∵A(﹣1,0)B(﹣5,0),∴A′(2m+1,0),B′(2m+5,0),
当B′在点C、D之间时,则重合部分为线段CB′,且C(6,0),
∴2m+5﹣6=2,解得m=;
当A′在点C、D之间时,则重合部分为线段A′D,且D(15,0),
∴15﹣(2m+1)=2,解得m=6;
综上可知m的值为或6.
