1.1.1 空间向量及其线性运算 课件(共30张PPT)
文档属性
| 名称 | 1.1.1 空间向量及其线性运算 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 14:41:41 | ||
图片预览










文档简介
(共30张PPT)
1.1.1空间向量及其线性运算
1.了解空间向量的概念.
2.掌握空间向量的加减运算、数乘运算. (重点)
3.共线向量及共面向量的应用.(重点、难点)
学习目标:1分钟
情景引入
太原崛围上风景秀美,在崛围山风景区航空飞行营地,2018年举行了“绿宇杯”山西滑翔伞邀请赛。
这是一个做滑翔伞运动的场景.可以想象,在滑翔过程中,飞行员会受到来自不同方向、大小各异的力.
思考:这些力在同一个平面上吗?
起点
终点
概念
与向量a长度相等而方向相反的向量,叫做a的相反向量
空间向量的相关概念
长度为0的向量
模为1的向量
如果表示若干空间向量的有向线段所在的直线
互相平行或重合,那么这些向量叫做共线向量
方向相同且模相等的向量
∥
∥
A
B
a
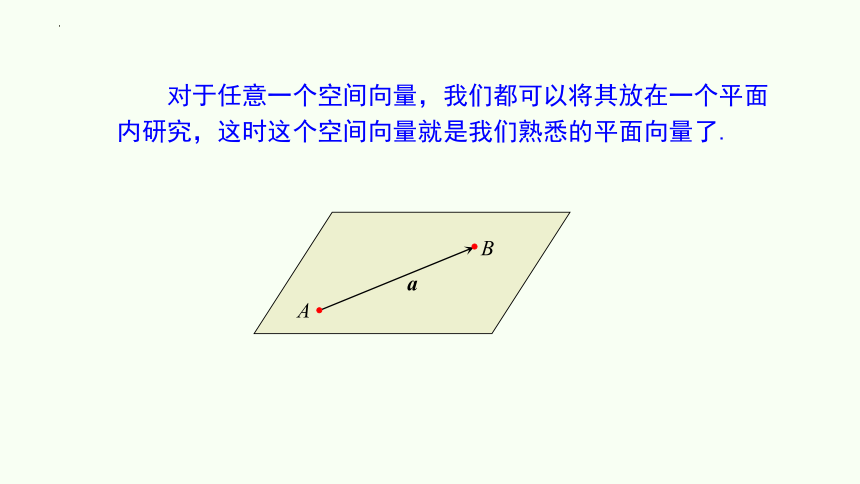
对于任意一个空间向量,我们都可以将其放在一个平面内研究,这时这个空间向量就是我们熟悉的平面向量了.
α
空间向量是自由的,所以对于空间中的任意两个非零向量,我们都可以通过平移使它们的起点重合.
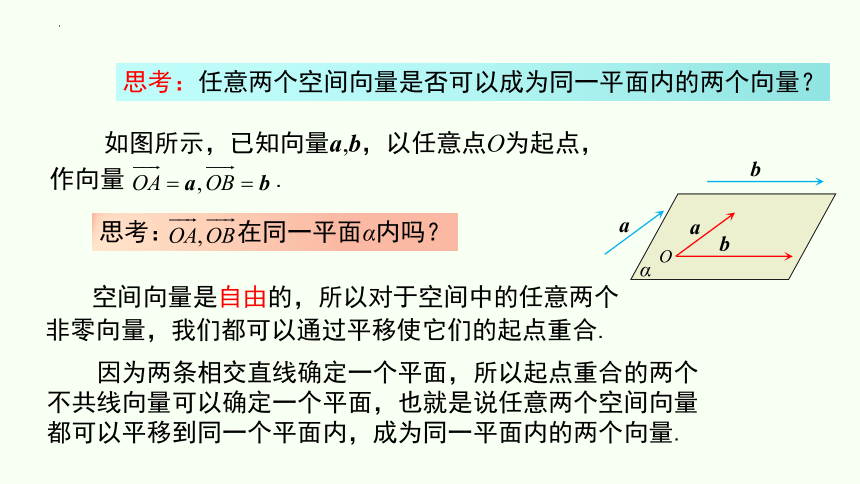
如图所示,已知向量a,b,以任意点O为起点,作向量 .
思考: 在同一平面α内吗?
思考:任意两个空间向量是否可以成为同一平面内的两个向量?
b
a
O
b
a
因为两条相交直线确定一个平面,所以起点重合的两个不共线向量可以确定一个平面,也就是说任意两个空间向量都可以平移到同一个平面内,成为同一平面内的两个向量.
问题
在学面向量的相关概念后,我们研究了平面向量的线性运算,你能类比平面向量,研究空间向量的线性运算吗?
思考 空间中的任意两个向量是不是共面的?
是,空间中的任意两个向量都可以平移到同一个平面内,成为同一平面内的两个向量.
空间向量的线性运算 加法
减法
数乘
空间向量的运算(同平面向量)
当λ=0时,λa=0
想一想 向量起点的选择对向量线性运算的结果有影响吗?
没有影响,向量起点可以平移到任何位置.
空间向量的运算律
运算律
交换律:+=+;
结合律:+(+)=(+)+,λ(μ)=(λμ);
分配律:(λ+μ)=λ+μ,λ(+)=λ+λ.
(3)当≠0,≠0且≠0,≠1时,可分如下两种情况:
①当>0且≠1时,如图,在平面内任取一点,作=, =, =, =,则=+, =+.
由作法知∥,∠=∠,| |=λ||.所以=.所以∽.
所以=,∠=∠.
因此点,,在同一条直线上,||=||, 与的方向也相同.所以(+)=+.
②当<0时,可类似证明(+)=+.
思考 怎样作图表示三个向量的和,作出的和向量是否与相加的顺序有关?
可以利用三角形法则和平行四边形法则作出三个向量的和.加法运算是对有限个向量求和,交换相加向量的顺序,其和不变.
思考 由数乘λa=0,可否得出λ=0
不能.λa=0 λ=0或a=0.
探究 如图示,在平行六面体ABCD-A′B′C′D′ (底面是平行四边形的四棱柱) 中,分别标出 , 表示的向量. 从中体会向量加法运算的交换律及结合律. 一般地,三个不共面的向量的和与这三个向量有什么关系?
A
C
D
B
C′
D′
B′
A′
三个不共面的向量的和与这三个向量的关系:
三个不共面的向量的和就是以这三个不共面的向量为邻边的平行六面体的对角线所在向量.
另外,利用向量加法的交换律和结合律,还可以得到: 有限个向量求和,交换相加向量的顺序,其和不变.
教材第5页练习
A
C
D
B
C′
D′
B′
A′
E
F
教材第5页练习
A
C
D
B
C′
D′
B′
A′
E
F
新知探索
问题:对任意两个空间向量与,如果,与有什么位置关系?反过来,与有什么位置关系时,?
类似于平面向量共线的充要条件,对任意两个空间向量,,的充要条件是存在实数,使.
如图,是直线上一点,在直线上取非零向量,则对于直线上任意一点,由数乘向量的定义及向量共线的充要条件可知,存在实数,使得.
新知探索
我们把与向量平行的非零向量称为直线的方向向量.这样,直线上任意一点都可以由直线上的一点和它的方向向量表示,也就是说,直线可以由其上一点和它的方向向量确定.
概念生成
共面向量:平行于同一平面的向量,叫做共面向量.
O
A
向量可以进行平移
平行即共面
问题 平面向量基本定理是什么?
平面向量基本定理:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
向量可以进行平移
平面向量基本定理也可以是共面向量定理
概念生成
注意:
(1)向量可以进行平移的
(2)空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。
(3)判断三个向量是否共面
向量共面的充要条件:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
A
B
C
D
A1
B1
C1
D1
例题讲解
O
A
B
C
D
E
F
G
H
思路探究:欲证 四点共面,只需证明
共面.而由已知 共面,可以利用向量运算由
共面的表达式推得 共面的表达式.
例:如图,已知平行四边形 ,过平面 外一点 ,
作射线 ,在四条射线上分别取点 ,使
.
求证: 四点共面.
考点:空间中四点共面的判定.
O
A
B
C
D
E
F
G
H
是平行四边形
由向量共面的充要条件可知, 共面,又 过同一
点 ,从而 四点共面.
证明: .
A
M
C
G
D
B
D
ABD
A
B
C
D
A1
B1
C1
D1
A
B
C
D
A’
B’
C’
D’
E
F
小结
1.空间向量的定义及表示方法
2.空间向量的线性运算与运算律
3.空间向量的简单运用
本课结束
“
”
1.1.1空间向量及其线性运算
1.了解空间向量的概念.
2.掌握空间向量的加减运算、数乘运算. (重点)
3.共线向量及共面向量的应用.(重点、难点)
学习目标:1分钟
情景引入
太原崛围上风景秀美,在崛围山风景区航空飞行营地,2018年举行了“绿宇杯”山西滑翔伞邀请赛。
这是一个做滑翔伞运动的场景.可以想象,在滑翔过程中,飞行员会受到来自不同方向、大小各异的力.
思考:这些力在同一个平面上吗?
起点
终点
概念
与向量a长度相等而方向相反的向量,叫做a的相反向量
空间向量的相关概念
长度为0的向量
模为1的向量
如果表示若干空间向量的有向线段所在的直线
互相平行或重合,那么这些向量叫做共线向量
方向相同且模相等的向量
∥
∥
A
B
a
对于任意一个空间向量,我们都可以将其放在一个平面内研究,这时这个空间向量就是我们熟悉的平面向量了.
α
空间向量是自由的,所以对于空间中的任意两个非零向量,我们都可以通过平移使它们的起点重合.
如图所示,已知向量a,b,以任意点O为起点,作向量 .
思考: 在同一平面α内吗?
思考:任意两个空间向量是否可以成为同一平面内的两个向量?
b
a
O
b
a
因为两条相交直线确定一个平面,所以起点重合的两个不共线向量可以确定一个平面,也就是说任意两个空间向量都可以平移到同一个平面内,成为同一平面内的两个向量.
问题
在学面向量的相关概念后,我们研究了平面向量的线性运算,你能类比平面向量,研究空间向量的线性运算吗?
思考 空间中的任意两个向量是不是共面的?
是,空间中的任意两个向量都可以平移到同一个平面内,成为同一平面内的两个向量.
空间向量的线性运算 加法
减法
数乘
空间向量的运算(同平面向量)
当λ=0时,λa=0
想一想 向量起点的选择对向量线性运算的结果有影响吗?
没有影响,向量起点可以平移到任何位置.
空间向量的运算律
运算律
交换律:+=+;
结合律:+(+)=(+)+,λ(μ)=(λμ);
分配律:(λ+μ)=λ+μ,λ(+)=λ+λ.
(3)当≠0,≠0且≠0,≠1时,可分如下两种情况:
①当>0且≠1时,如图,在平面内任取一点,作=, =, =, =,则=+, =+.
由作法知∥,∠=∠,| |=λ||.所以=.所以∽.
所以=,∠=∠.
因此点,,在同一条直线上,||=||, 与的方向也相同.所以(+)=+.
②当<0时,可类似证明(+)=+.
思考 怎样作图表示三个向量的和,作出的和向量是否与相加的顺序有关?
可以利用三角形法则和平行四边形法则作出三个向量的和.加法运算是对有限个向量求和,交换相加向量的顺序,其和不变.
思考 由数乘λa=0,可否得出λ=0
不能.λa=0 λ=0或a=0.
探究 如图示,在平行六面体ABCD-A′B′C′D′ (底面是平行四边形的四棱柱) 中,分别标出 , 表示的向量. 从中体会向量加法运算的交换律及结合律. 一般地,三个不共面的向量的和与这三个向量有什么关系?
A
C
D
B
C′
D′
B′
A′
三个不共面的向量的和与这三个向量的关系:
三个不共面的向量的和就是以这三个不共面的向量为邻边的平行六面体的对角线所在向量.
另外,利用向量加法的交换律和结合律,还可以得到: 有限个向量求和,交换相加向量的顺序,其和不变.
教材第5页练习
A
C
D
B
C′
D′
B′
A′
E
F
教材第5页练习
A
C
D
B
C′
D′
B′
A′
E
F
新知探索
问题:对任意两个空间向量与,如果,与有什么位置关系?反过来,与有什么位置关系时,?
类似于平面向量共线的充要条件,对任意两个空间向量,,的充要条件是存在实数,使.
如图,是直线上一点,在直线上取非零向量,则对于直线上任意一点,由数乘向量的定义及向量共线的充要条件可知,存在实数,使得.
新知探索
我们把与向量平行的非零向量称为直线的方向向量.这样,直线上任意一点都可以由直线上的一点和它的方向向量表示,也就是说,直线可以由其上一点和它的方向向量确定.
概念生成
共面向量:平行于同一平面的向量,叫做共面向量.
O
A
向量可以进行平移
平行即共面
问题 平面向量基本定理是什么?
平面向量基本定理:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
向量可以进行平移
平面向量基本定理也可以是共面向量定理
概念生成
注意:
(1)向量可以进行平移的
(2)空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。
(3)判断三个向量是否共面
向量共面的充要条件:如果两个向量不共线,则向量与向量共面的充要条件是存在唯一的有序实数对(x,y)使.
A
B
C
D
A1
B1
C1
D1
例题讲解
O
A
B
C
D
E
F
G
H
思路探究:欲证 四点共面,只需证明
共面.而由已知 共面,可以利用向量运算由
共面的表达式推得 共面的表达式.
例:如图,已知平行四边形 ,过平面 外一点 ,
作射线 ,在四条射线上分别取点 ,使
.
求证: 四点共面.
考点:空间中四点共面的判定.
O
A
B
C
D
E
F
G
H
是平行四边形
由向量共面的充要条件可知, 共面,又 过同一
点 ,从而 四点共面.
证明: .
A
M
C
G
D
B
D
ABD
A
B
C
D
A1
B1
C1
D1
A
B
C
D
A’
B’
C’
D’
E
F
小结
1.空间向量的定义及表示方法
2.空间向量的线性运算与运算律
3.空间向量的简单运用
本课结束
“
”
