1.1.1空间向量及其线性运算 课件(共37张PPT)
文档属性
| 名称 | 1.1.1空间向量及其线性运算 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 14:45:12 | ||
图片预览









文档简介
(共37张PPT)
人教A版2019高中数学选择性必修第一册
第一章 空间向量与立体几何
1.1.1 空间向量及其线性运算
新知探究
2
新知引入
教学目标:
(1)经历向量及其运算由平面向空间推广的过程,了解空间向量的概念,发展
数学抽象素养;
(2)掌握空间向量的加法、减法、数乘运算及其表示;
(3)掌握空间向量加法、减法、数乘的运算律;
(4)借助向量的线性运算的学习,提升数学运算素养.
教学重点:空间向量的概念和线性运算及其应用
教学难点:空间向量的线性运算及其应用
【问题引入】
在空间中一个正三棱锥A-BCD,有三个相同的力 a,b,c 作用在这个三棱锥上,其中力a,b,c的方向在分别直线AB、AC、AD上,且该这个三棱锥重400N。
问:这个三棱锥会在这三个力的作用下做什么运动?
当这三个力多大时,这个三棱锥会运动?
【问题1】
1.在这个问题中,我们研究的是力,在数学中,这些力可以看做是什么量?
2.这些量与我们以往学过的有什么不同?
3.我们能不能依据以往学过的知识来解决这个空间问题?
【问题2】
1.如右图,向量如何表示?其模如何表示?
2.零向量和单位向量如何定义表示?
3.空间中某两个向量模长一样但方向相反的向量是什么向量?
4.空间中某两个向量平行或重合,这两个向量称为什么
5.方向和模长都一样的向量称为?
a
A
B
【问题3】
空间中的向量如何线性计算?
有什么方法可以用平面向量中的计算方法来计算空间向量?
探究:我们已经学面向量的概念,我们能否根据平面向量的概念类比得出空间向量的概念?
我们一起回忆一下平面向量的相关概念,类比的得出空间向量的概念
点拨精讲
问题1 平面向量是什么?我们是如何表示平面向量的?
平面向量 空间向量
定义
表示
起点
终点
?
平面中既有大小又有方向的量
1.或者是
2.坐标表示
平面向量 空间向量
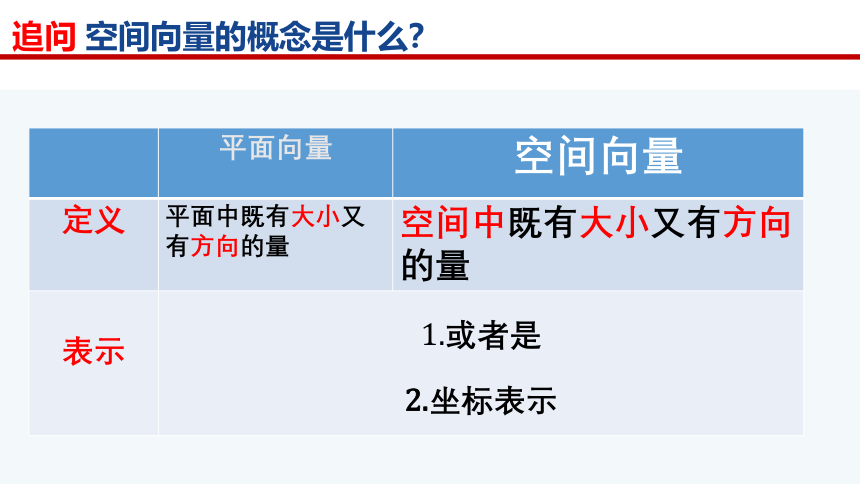
定义 平面中既有大小又有方向的量 空间中既有大小又有方向的量
表示 1.或者是 2.坐标表示
追问 空间向量的概念是什么?
1. 空间向量的概念
2. 空间向量的模及表示方法
与平面向量一样,空间向量也用有向线段表示. 有向线段的长度表示向量的模.
与平面向量一样,在空间,我们把具有大小和方向的量叫做空间向量. 空间向量的大小叫做空间向量的长度或模. 空间向量用黑体字母a,b,c,···表示. (注意:印刷体才用黑体a表示,而书写体一定要加箭头,即 )
C
A
B
O
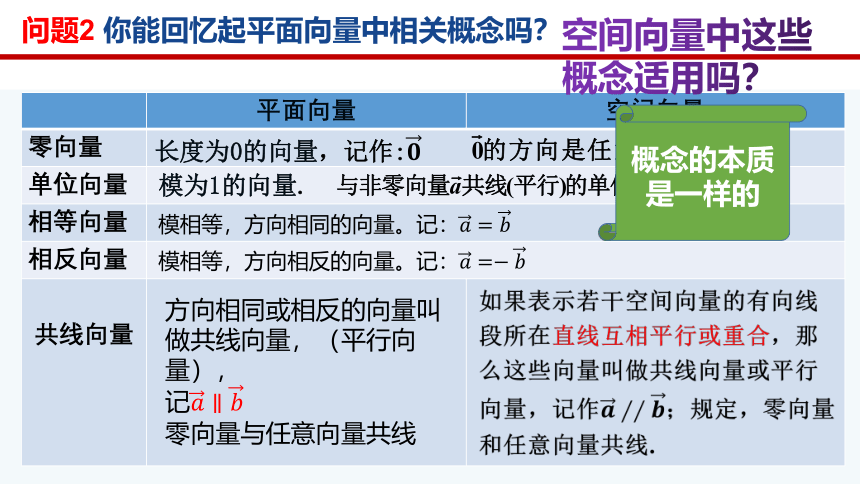
问题2 你能回忆起平面向量中相关概念吗?
平面向量 空间向量
零向量
单位向量
相等向量
相反向量
共线向量
长度为0的向量,记作:
模为1的向量.
模相等,方向相同的向量。记:
模相等,方向相反的向量。记:
空间向量中这些概念适用吗?
方向相同或相反的向量叫做共线向量,(平行向量),
记
零向量与任意向量共线
概念的本质是一样的
因此,在空间,同向且等长的有向线段表示同一向量或相等向量. 空间向量是自由的,所以对于空间中的任意两个非零向量,我们都可以通过平移使它们的起点重合. 因为两条相交直线确定一个平面,所以起点重合的两个不共线向量可以确定一个平面,也就是说,任意两个空间向量都可以平移到同一个平面内,成为同一平面内的两个向量.
这样就使得所有空间向量问题都可以转变成平面向量解决.
空间向量的线性运算 加法
减法
数乘
运算律
空间向量的线性运算和运算律
交换律:a+b=b+a
结合律:a+(b+c)=(a+b)+c,λ(μa)=(λμ)a
分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb
空间向量的加减运算
空间任意两个向量是否一定能够平移到同一个平面中?
在空间中,任意两个向量都可以平移到同一个平面内,所以空间两个向量的加法和减法运算与平面向量相同.
空间向量的加法的运算律.
问题:平面向量的加法运算符合交换律和结合律,空间向量是否也符合?能否借助平行六面体图形证明?
⑴加法交换律: ;
⑵加法结合律: ;
空间向量的加减运算
如图,已知平行六面体ABCDA′B′C′D′,化简下列表达式.
规律总结
掌握好向量加减法的三角形法则是解决这类问题的关键,灵活应用相反向量、相等向量及两向量和、差,可使这类题迅速获解;
0
解 方法一(转化为加法运算)
方法二(转化为减法运算)
空间向量的线性运算及其运算律
解(1)∵P是C1D1的中点,
空间向量的线性运算及其运算律
解(2)∵N是BC的中点,
空间向量的线性运算及其运算律
解(3)∵M是AA1的中点,
空间向量的线性运算及其运算律
《二》利用数乘运算进行向量表示的技巧
空间向量的线性运算及其运算律
(1)用反向量:向量的三角形法则是解决空间向量加法、减法的关键,灵活运用相反向量可使向量首尾相接.
(2)用平移:利用三角形法则和平行四边形法则进行向量加、减法运算时,务必注意和向量、差向量的方向,
必要时可采用空间向量的自由平移获得运算结果.
【悟】 《一》空间向量加法、减法运算的两个技巧
(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三角形法则、平行四边形法则,将目标向量
转化为已知向量.
(2)明确目标:在化简过程中要有目标意识,巧妙运用中点性质.
探究:对任意两个空间向量与,如果,与有什么位置关系?反过来,与有什么位置关系时,?
共线向量定理:对任意两个空间向量,,的充要条件是存在实数,使.
向量共线定理
如图,是直线上一点,在直线上取非零向量,则对于直线上任意一点,由数乘向量的定义及向量共线的充要条件可知,存在实数,使得.
直线的方向向量
如图,如果表示向量的有向线段所在的直线与直线平行或重合,那么称向量平行于直线.如果直线平行于平面或在平面内,那么称向量平行于平面.平行于同一个平面的向量,叫做共面向量.
共面向量
我们知道,任意两个空间向量总是共面的,但三个空间向量既可能是共面的,也可能是不共面的.那么,什么情况下三个空间向量共面呢?
探究:对平面内任意两个不共线向量,,由平面向量基本定理可知,这个平面内的任意一个向量可以写成其中是唯一确定的有序数对.对两个不共线的空间向量,如果那么向量与向量有什
么位置关系?反过来,向量与有什么位置关系时,?
向量共面定理:如果两个向量不共线,那么向量与共面的充要条件是存在唯一的有序实数对,使.
向量共面定理
O
A
C
B
P
①空间一点P位于平面ABC内的充要条件是存在有序实数对(x,y),使
②P、A、B、C四点共面的充要条件是对空间任意一点O,
共面向量定理推论
课堂练习
例 如图,已知平行四边形ABCD,从平面AC外一点O作射线OA,OB,OC,OD,在四条射线上分别取点E,F,G,H,使
求证:E,F,G,H四点共面
课堂练习
证明:
·
追问:最终的结果你还有没有其他的表示方法?能得到什么结论?
1.对于空间任意一点O,下列命题正确的是:
(A)若 ,则P、A、B共线
(B)若 ,则P是AB的中点
(C)若 ,则P、A、B不共线
(D)若 ,则P、A、B共线
2.已知点M在平面ABC内,并且对空间任意一点
O, , 则x的值为( )
巩固练习
3.下列说明正确的是: (A)在平面内共线的向量在空间不一定共线
(B)在空间共线的向量在平面内不一定共线
(C)在平面内共线的向量在空间一定不共线
(D)在空间共线的向量在平面内一定共线
4.下列说法正确的是: (A)平面内的任意两个向量都共线
(B)空间的任意三个向量都不共面
(C)空间的任意两个向量都共面
(D)空间的任意三个向量都共面
巩固练习
A
B
M
C
G
D
(2)原式
5.在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简
巩固练习
A
B
C
D
D
C
B
A
6.在立方体AC1中,点E是面A’C’的中心,求下列各式中的x,y.
E
答案: (1)x=1
(2)x=y=1/2
巩固练习
A
M
C
G
D
B
小结
1.空间向量的定义及表示方法
2.空间向量的线性运算与运算律
3.空间向量的简单运用
谢
谢
聆
听
人教A版2019高中数学选择性必修第一册
第一章 空间向量与立体几何
1.1.1 空间向量及其线性运算
新知探究
2
新知引入
教学目标:
(1)经历向量及其运算由平面向空间推广的过程,了解空间向量的概念,发展
数学抽象素养;
(2)掌握空间向量的加法、减法、数乘运算及其表示;
(3)掌握空间向量加法、减法、数乘的运算律;
(4)借助向量的线性运算的学习,提升数学运算素养.
教学重点:空间向量的概念和线性运算及其应用
教学难点:空间向量的线性运算及其应用
【问题引入】
在空间中一个正三棱锥A-BCD,有三个相同的力 a,b,c 作用在这个三棱锥上,其中力a,b,c的方向在分别直线AB、AC、AD上,且该这个三棱锥重400N。
问:这个三棱锥会在这三个力的作用下做什么运动?
当这三个力多大时,这个三棱锥会运动?
【问题1】
1.在这个问题中,我们研究的是力,在数学中,这些力可以看做是什么量?
2.这些量与我们以往学过的有什么不同?
3.我们能不能依据以往学过的知识来解决这个空间问题?
【问题2】
1.如右图,向量如何表示?其模如何表示?
2.零向量和单位向量如何定义表示?
3.空间中某两个向量模长一样但方向相反的向量是什么向量?
4.空间中某两个向量平行或重合,这两个向量称为什么
5.方向和模长都一样的向量称为?
a
A
B
【问题3】
空间中的向量如何线性计算?
有什么方法可以用平面向量中的计算方法来计算空间向量?
探究:我们已经学面向量的概念,我们能否根据平面向量的概念类比得出空间向量的概念?
我们一起回忆一下平面向量的相关概念,类比的得出空间向量的概念
点拨精讲
问题1 平面向量是什么?我们是如何表示平面向量的?
平面向量 空间向量
定义
表示
起点
终点
?
平面中既有大小又有方向的量
1.或者是
2.坐标表示
平面向量 空间向量
定义 平面中既有大小又有方向的量 空间中既有大小又有方向的量
表示 1.或者是 2.坐标表示
追问 空间向量的概念是什么?
1. 空间向量的概念
2. 空间向量的模及表示方法
与平面向量一样,空间向量也用有向线段表示. 有向线段的长度表示向量的模.
与平面向量一样,在空间,我们把具有大小和方向的量叫做空间向量. 空间向量的大小叫做空间向量的长度或模. 空间向量用黑体字母a,b,c,···表示. (注意:印刷体才用黑体a表示,而书写体一定要加箭头,即 )
C
A
B
O
问题2 你能回忆起平面向量中相关概念吗?
平面向量 空间向量
零向量
单位向量
相等向量
相反向量
共线向量
长度为0的向量,记作:
模为1的向量.
模相等,方向相同的向量。记:
模相等,方向相反的向量。记:
空间向量中这些概念适用吗?
方向相同或相反的向量叫做共线向量,(平行向量),
记
零向量与任意向量共线
概念的本质是一样的
因此,在空间,同向且等长的有向线段表示同一向量或相等向量. 空间向量是自由的,所以对于空间中的任意两个非零向量,我们都可以通过平移使它们的起点重合. 因为两条相交直线确定一个平面,所以起点重合的两个不共线向量可以确定一个平面,也就是说,任意两个空间向量都可以平移到同一个平面内,成为同一平面内的两个向量.
这样就使得所有空间向量问题都可以转变成平面向量解决.
空间向量的线性运算 加法
减法
数乘
运算律
空间向量的线性运算和运算律
交换律:a+b=b+a
结合律:a+(b+c)=(a+b)+c,λ(μa)=(λμ)a
分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb
空间向量的加减运算
空间任意两个向量是否一定能够平移到同一个平面中?
在空间中,任意两个向量都可以平移到同一个平面内,所以空间两个向量的加法和减法运算与平面向量相同.
空间向量的加法的运算律.
问题:平面向量的加法运算符合交换律和结合律,空间向量是否也符合?能否借助平行六面体图形证明?
⑴加法交换律: ;
⑵加法结合律: ;
空间向量的加减运算
如图,已知平行六面体ABCDA′B′C′D′,化简下列表达式.
规律总结
掌握好向量加减法的三角形法则是解决这类问题的关键,灵活应用相反向量、相等向量及两向量和、差,可使这类题迅速获解;
0
解 方法一(转化为加法运算)
方法二(转化为减法运算)
空间向量的线性运算及其运算律
解(1)∵P是C1D1的中点,
空间向量的线性运算及其运算律
解(2)∵N是BC的中点,
空间向量的线性运算及其运算律
解(3)∵M是AA1的中点,
空间向量的线性运算及其运算律
《二》利用数乘运算进行向量表示的技巧
空间向量的线性运算及其运算律
(1)用反向量:向量的三角形法则是解决空间向量加法、减法的关键,灵活运用相反向量可使向量首尾相接.
(2)用平移:利用三角形法则和平行四边形法则进行向量加、减法运算时,务必注意和向量、差向量的方向,
必要时可采用空间向量的自由平移获得运算结果.
【悟】 《一》空间向量加法、减法运算的两个技巧
(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三角形法则、平行四边形法则,将目标向量
转化为已知向量.
(2)明确目标:在化简过程中要有目标意识,巧妙运用中点性质.
探究:对任意两个空间向量与,如果,与有什么位置关系?反过来,与有什么位置关系时,?
共线向量定理:对任意两个空间向量,,的充要条件是存在实数,使.
向量共线定理
如图,是直线上一点,在直线上取非零向量,则对于直线上任意一点,由数乘向量的定义及向量共线的充要条件可知,存在实数,使得.
直线的方向向量
如图,如果表示向量的有向线段所在的直线与直线平行或重合,那么称向量平行于直线.如果直线平行于平面或在平面内,那么称向量平行于平面.平行于同一个平面的向量,叫做共面向量.
共面向量
我们知道,任意两个空间向量总是共面的,但三个空间向量既可能是共面的,也可能是不共面的.那么,什么情况下三个空间向量共面呢?
探究:对平面内任意两个不共线向量,,由平面向量基本定理可知,这个平面内的任意一个向量可以写成其中是唯一确定的有序数对.对两个不共线的空间向量,如果那么向量与向量有什
么位置关系?反过来,向量与有什么位置关系时,?
向量共面定理:如果两个向量不共线,那么向量与共面的充要条件是存在唯一的有序实数对,使.
向量共面定理
O
A
C
B
P
①空间一点P位于平面ABC内的充要条件是存在有序实数对(x,y),使
②P、A、B、C四点共面的充要条件是对空间任意一点O,
共面向量定理推论
课堂练习
例 如图,已知平行四边形ABCD,从平面AC外一点O作射线OA,OB,OC,OD,在四条射线上分别取点E,F,G,H,使
求证:E,F,G,H四点共面
课堂练习
证明:
·
追问:最终的结果你还有没有其他的表示方法?能得到什么结论?
1.对于空间任意一点O,下列命题正确的是:
(A)若 ,则P、A、B共线
(B)若 ,则P是AB的中点
(C)若 ,则P、A、B不共线
(D)若 ,则P、A、B共线
2.已知点M在平面ABC内,并且对空间任意一点
O, , 则x的值为( )
巩固练习
3.下列说明正确的是: (A)在平面内共线的向量在空间不一定共线
(B)在空间共线的向量在平面内不一定共线
(C)在平面内共线的向量在空间一定不共线
(D)在空间共线的向量在平面内一定共线
4.下列说法正确的是: (A)平面内的任意两个向量都共线
(B)空间的任意三个向量都不共面
(C)空间的任意两个向量都共面
(D)空间的任意三个向量都共面
巩固练习
A
B
M
C
G
D
(2)原式
5.在空间四边形ABCD中,点M、G分别是BC、CD边的中点,化简
巩固练习
A
B
C
D
D
C
B
A
6.在立方体AC1中,点E是面A’C’的中心,求下列各式中的x,y.
E
答案: (1)x=1
(2)x=y=1/2
巩固练习
A
M
C
G
D
B
小结
1.空间向量的定义及表示方法
2.空间向量的线性运算与运算律
3.空间向量的简单运用
谢
谢
聆
听
