初中数学北师大版八上4.4.3 一次函数的综合应用教案
文档属性
| 名称 | 初中数学北师大版八上4.4.3 一次函数的综合应用教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 274.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 00:00:00 | ||
图片预览


文档简介
4.4.3 一次函数的综合应用
一、教学任务分析
本节课教学目标:
1.进一步训练学生的识图能力,能通过函数图象获取信息,解决简单的实际问题;
2.在函数图象信息获取过程中,进一步培养学生的数形结合意识,发展形象思维;
3.在解决实际问题过程中,进一步发展学生的分析问题、解决问题的能力和数学应用意识.
4.在现实问题的解决中,使学生初步认识数学与人类生活的密切联系,从而培养学生学习数学的兴趣.
教学重点
一次函数图象的应用
教学难点
从函数图象中正确读取信息
二、教学过程
(一)、新课导入
观察下图,你能发现它们三条函数直线之间的差别吗?
上节课我们学习了一次函数在水库蓄水量与干旱持续时间方面的应用,还有一次函数在摩托车油箱中的剩余油量与行驶路程方面的应用,一次函数的应用不仅仅是在这两个方面,本节课我们继续学习它的应用.
(二)、讲授新课
1、例题讲解
如上图,l1反映了某公司产品的销售收入与销售量的关系, l 2反映了该公司产品的销售量的关系,根据图象填空.
①当销售量为2吨时,销售收入=_______元,销售成本=_____元;
②当销售量为6吨时,销售收入=________元,销售成本=_____元;
③当销售量等于______时,销售收入等于销售成本;
④当销售量________时,该公司赢利(收入大于成本);当销售量_______时,该公亏损(收入小于成本);
⑤l1对应的函数表达式是_______;l2对应的函数表达式是________________.
分析:(1)当销售量为2吨时,销售收入=2000元,销售成本为3000元;
(2)当销售量为6吨时,销售收入=6000元,销售成本=5000元;
(3)当销售量等于4吨时,销售收入等于销售成本;
(4)当销售量大于4号时,该公司赢利,当销售量小于4吨时,该公司亏损.
(5)l1经过原点和(4,4000),设表达式为y=kx,把(4,4000)代入,得
4000=4k,所以k=1000
所以l1的表达式为y=1000x,l2经过点(0,2000)和(4,4000),设表达式为y=kx+b.
根据题意,得
b=2000 ①
4k+b=4000 ②
把①代入②,得4k+2000=4000,所以k=500
所以l2的表达式为y=500x+2000
想一想:
l1 :y=1000x和l2 :y=500x+2000中的k和b的实际意义各是什么?
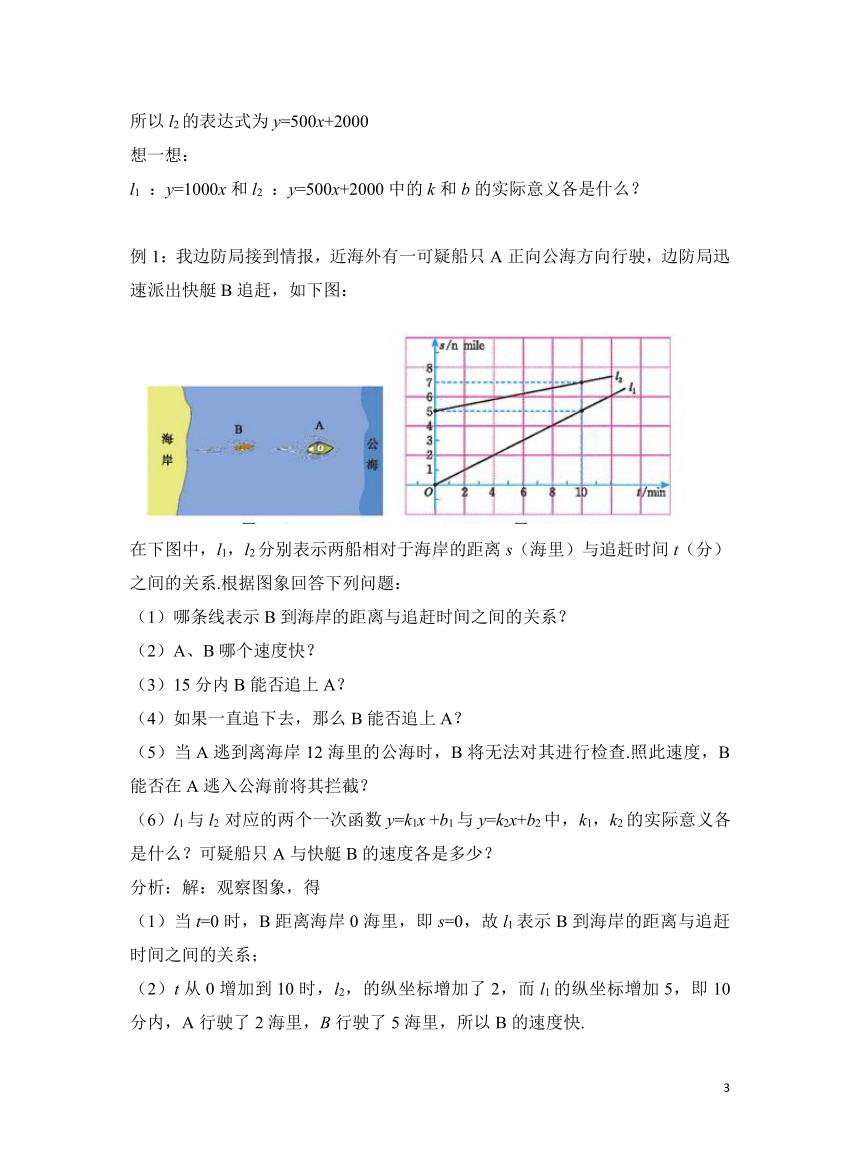
例1:我边防局接到情报,近海外有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶,如下图:
在下图中,l1,l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.根据图象回答下列问题:
(1)哪条线表示B到海岸的距离与追赶时间之间的关系?
(2)A、B哪个速度快?
(3)15分内B能否追上A?
(4)如果一直追下去,那么B能否追上A?
(5)当A逃到离海岸12海里的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截?
(6)l1与l2 对应的两个一次函数y=k1x +b1与y=k2x+b2中,k1,k2的实际意义各是什么?可疑船只A与快艇B的速度各是多少?
分析:解:观察图象,得
(1)当t=0时,B距离海岸0海里,即s=0,故l1表示B到海岸的距离与追赶时间之间的关系;
(2)t从0增加到10时,l2,的纵坐标增加了2,而l1的纵坐标增加5,即10分内,A行驶了2海里,B行驶了5海里,所以B的速度快.
(3)延长l1,l2,可以看出,当t=15时,l1上对应点在l2上对应点的下方,这表明,15分时B尚未追上A.
(4)如下图,l1,l2相交于点P,因此,如果一直追直去,那么B一定能追上A.
(5)下图中,l1与l2交点P的纵坐标小于12,这说明在A逃入公海前,我边防快艇B能够追上A.
(6) k1表示快艇B的速度,k2表示可疑船只A的速度.可疑船只A的速度是0.2 n mile/min,快艇B的速度是0.5 n mile/min.
练一练:下图 l1, l2 分别是龟兔赛跑中s-t函数图象.
(1)这一次是 m赛跑.
(2)表示兔子的图象是 .
(3)当兔子到达终点时,乌龟距终点还有 m;
(4)乌龟要与兔子同时到达终点乌龟要先跑 m;
(5)乌龟要先到达终点,至少要比兔子早跑 min;
例2:已知一次函数和的图象都经过点A(-4,0),且与y轴分别交于B、C两点,求△ABC的面积.
解:∵与的图象都过点A(-4,0),
∴ ,.
∴,.
∴两个一次函数分别是和.
∵与y轴交于点B,则,∴B(0,6);
∵与y轴交于点C,则y=-2,∴C(0,-2).
如图所示,
(三)、当堂练习:
1. 如图,射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差 km/h.
2.一次越野跑中,当小明跑了1600 m时,小刚跑了1400 m ,小明、小刚所跑的路程y(m)与时间t(s)之间的函数关系如图,则这次越野跑的全程为 m.
3.小亮和小明周六到距学校24 km的滨湖湿地公园春游,小亮8:00从学校出发,骑自行车去湿地公园,小明8:30从学校出发,乘车沿相同路线去滨湖湿地公园,在同一直角坐标系中,小亮和小明的行进路程s(km)与时间t(h)的函数图象如图所示.根据图象得到结论,其中错误的是( )
A.小亮骑自行车的平均速度是12 km/h
B.小明比小亮提前0.5小时到达滨湖湿地公园
C.小明在距学校12 km处追上小亮
D.9:30小明与小亮相距4 km
4.在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是 ,
从点燃到燃尽所用的时间分别是 .
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?
在什么时间段内,甲蜡烛比乙蜡烛高?
在什么时间段内,甲蜡烛比乙蜡烛低?
四、课后作业
P 95习题4.7
五、教学反思
通过函数图象来解决实际问题,使学生初步认识数学与人类生活的密切联系及对人类历史发展的作用,从而培养学生学习数学的兴趣,进一步训练学生的识图能力, 利用函数图象解决简单的实际问题.使他们能积极参与数学活动,进而更好地解决实际问题.
1
一、教学任务分析
本节课教学目标:
1.进一步训练学生的识图能力,能通过函数图象获取信息,解决简单的实际问题;
2.在函数图象信息获取过程中,进一步培养学生的数形结合意识,发展形象思维;
3.在解决实际问题过程中,进一步发展学生的分析问题、解决问题的能力和数学应用意识.
4.在现实问题的解决中,使学生初步认识数学与人类生活的密切联系,从而培养学生学习数学的兴趣.
教学重点
一次函数图象的应用
教学难点
从函数图象中正确读取信息
二、教学过程
(一)、新课导入
观察下图,你能发现它们三条函数直线之间的差别吗?
上节课我们学习了一次函数在水库蓄水量与干旱持续时间方面的应用,还有一次函数在摩托车油箱中的剩余油量与行驶路程方面的应用,一次函数的应用不仅仅是在这两个方面,本节课我们继续学习它的应用.
(二)、讲授新课
1、例题讲解
如上图,l1反映了某公司产品的销售收入与销售量的关系, l 2反映了该公司产品的销售量的关系,根据图象填空.
①当销售量为2吨时,销售收入=_______元,销售成本=_____元;
②当销售量为6吨时,销售收入=________元,销售成本=_____元;
③当销售量等于______时,销售收入等于销售成本;
④当销售量________时,该公司赢利(收入大于成本);当销售量_______时,该公亏损(收入小于成本);
⑤l1对应的函数表达式是_______;l2对应的函数表达式是________________.
分析:(1)当销售量为2吨时,销售收入=2000元,销售成本为3000元;
(2)当销售量为6吨时,销售收入=6000元,销售成本=5000元;
(3)当销售量等于4吨时,销售收入等于销售成本;
(4)当销售量大于4号时,该公司赢利,当销售量小于4吨时,该公司亏损.
(5)l1经过原点和(4,4000),设表达式为y=kx,把(4,4000)代入,得
4000=4k,所以k=1000
所以l1的表达式为y=1000x,l2经过点(0,2000)和(4,4000),设表达式为y=kx+b.
根据题意,得
b=2000 ①
4k+b=4000 ②
把①代入②,得4k+2000=4000,所以k=500
所以l2的表达式为y=500x+2000
想一想:
l1 :y=1000x和l2 :y=500x+2000中的k和b的实际意义各是什么?
例1:我边防局接到情报,近海外有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶,如下图:
在下图中,l1,l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.根据图象回答下列问题:
(1)哪条线表示B到海岸的距离与追赶时间之间的关系?
(2)A、B哪个速度快?
(3)15分内B能否追上A?
(4)如果一直追下去,那么B能否追上A?
(5)当A逃到离海岸12海里的公海时,B将无法对其进行检查.照此速度,B能否在A逃入公海前将其拦截?
(6)l1与l2 对应的两个一次函数y=k1x +b1与y=k2x+b2中,k1,k2的实际意义各是什么?可疑船只A与快艇B的速度各是多少?
分析:解:观察图象,得
(1)当t=0时,B距离海岸0海里,即s=0,故l1表示B到海岸的距离与追赶时间之间的关系;
(2)t从0增加到10时,l2,的纵坐标增加了2,而l1的纵坐标增加5,即10分内,A行驶了2海里,B行驶了5海里,所以B的速度快.
(3)延长l1,l2,可以看出,当t=15时,l1上对应点在l2上对应点的下方,这表明,15分时B尚未追上A.
(4)如下图,l1,l2相交于点P,因此,如果一直追直去,那么B一定能追上A.
(5)下图中,l1与l2交点P的纵坐标小于12,这说明在A逃入公海前,我边防快艇B能够追上A.
(6) k1表示快艇B的速度,k2表示可疑船只A的速度.可疑船只A的速度是0.2 n mile/min,快艇B的速度是0.5 n mile/min.
练一练:下图 l1, l2 分别是龟兔赛跑中s-t函数图象.
(1)这一次是 m赛跑.
(2)表示兔子的图象是 .
(3)当兔子到达终点时,乌龟距终点还有 m;
(4)乌龟要与兔子同时到达终点乌龟要先跑 m;
(5)乌龟要先到达终点,至少要比兔子早跑 min;
例2:已知一次函数和的图象都经过点A(-4,0),且与y轴分别交于B、C两点,求△ABC的面积.
解:∵与的图象都过点A(-4,0),
∴ ,.
∴,.
∴两个一次函数分别是和.
∵与y轴交于点B,则,∴B(0,6);
∵与y轴交于点C,则y=-2,∴C(0,-2).
如图所示,
(三)、当堂练习:
1. 如图,射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差 km/h.
2.一次越野跑中,当小明跑了1600 m时,小刚跑了1400 m ,小明、小刚所跑的路程y(m)与时间t(s)之间的函数关系如图,则这次越野跑的全程为 m.
3.小亮和小明周六到距学校24 km的滨湖湿地公园春游,小亮8:00从学校出发,骑自行车去湿地公园,小明8:30从学校出发,乘车沿相同路线去滨湖湿地公园,在同一直角坐标系中,小亮和小明的行进路程s(km)与时间t(h)的函数图象如图所示.根据图象得到结论,其中错误的是( )
A.小亮骑自行车的平均速度是12 km/h
B.小明比小亮提前0.5小时到达滨湖湿地公园
C.小明在距学校12 km处追上小亮
D.9:30小明与小亮相距4 km
4.在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是 ,
从点燃到燃尽所用的时间分别是 .
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?
在什么时间段内,甲蜡烛比乙蜡烛高?
在什么时间段内,甲蜡烛比乙蜡烛低?
四、课后作业
P 95习题4.7
五、教学反思
通过函数图象来解决实际问题,使学生初步认识数学与人类生活的密切联系及对人类历史发展的作用,从而培养学生学习数学的兴趣,进一步训练学生的识图能力, 利用函数图象解决简单的实际问题.使他们能积极参与数学活动,进而更好地解决实际问题.
1
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
