初中数学北师大版八上4.4.2 一次函数的实际应用教案
文档属性
| 名称 | 初中数学北师大版八上4.4.2 一次函数的实际应用教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 00:00:00 | ||
图片预览


文档简介
4.4.2 一次函数的实际应用
一、教学目标
1、能通过函数图象获取信息,发展形象思维.
2、能利用函数图象解决简单的实际问题,
3、初步体会方程与函数的关系.
二、教学重难点
重点:一次函数图象的应用.
难点:一元一次方程与一次函数的关系.
三、教学过程
1、新课导入
从一次函数图象可获得哪些信息
(1)由一次函数的图象可确定k 和 b 的符号;
(2)由一次函数的图象可估计函数的变化趋势;
(3)可直接观察出:x与y的对应值;
(4)由一次函数的图象与y轴的交点的坐标可确定b值,
从而确定一次函数的图象的表达式.
在前几节课里,我们分别学习了一次函数,一次函数的图象,一次函数图象的特征,并且了解到一次函数的应用十分广泛,和我们日常生活密切相关,因此本节课我们一起来学习一次函数图象的应用.
2、讲授新课
(1)由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少,干旱持续时间t(天)与蓄水量V(万米3)的关系如下图所示,回答下列问题:
①水库干旱前的蓄水量是多少?
②干旱持续10天,蓄水量为多少?连续干旱23天呢?
③蓄水量小于400万m3时,将发生严重干旱警报.干旱多少天后将发出严重干旱警报?
④按照这个规律,预计持续干旱多少天水库将干涸?
请大家根据图象回答问题,有困难的同学,请与同伴互相交流.
分析:
(1)1200万m3
(2)求干旱持续10天时的蓄水量,也就是求t等于10时所对应的V的值.当t=10时,V约为1000万m3。同理可知当t为23天时,V约为750万m3.
(3)当蓄水量小于400万m3时,将发出严重干旱警报,也就是当V等于400万m3时,求所对应的t值.t约为40天.
(4)水库干涸也就是V为0,所以求函数图象与横轴交点的横坐标即为所求.当V为0时,所对应的t的值约为60天.
例1 某种摩托车的油箱最多可储油10 L,加满油后,油箱中的剩余油量y(L)与摩托车行驶路程x (km)之间的关系如图所示.
根据图象回答下列问题:
(1)油箱最多可储油多少升?
(2)一箱汽油可供摩托车行驶多少千米?
(3)摩托车每行驶100 km消耗多少升汽油?
(4)油箱中的剩余油量小于1 L时,摩托车将自动报警,行驶多少千米后,摩托车将自动报警?
分析:(1)当 x=0时,y=10.因此,油箱最多可储油10 L.
(2)函数图象与x轴交点的横坐标即为摩托车行驶的最长路程.
(3)x从0增加到100时,y从10开始减少,减少的数量即为消耗的数量.
(4)当y小于1时,摩托车将自动报警.
3、应用与延伸
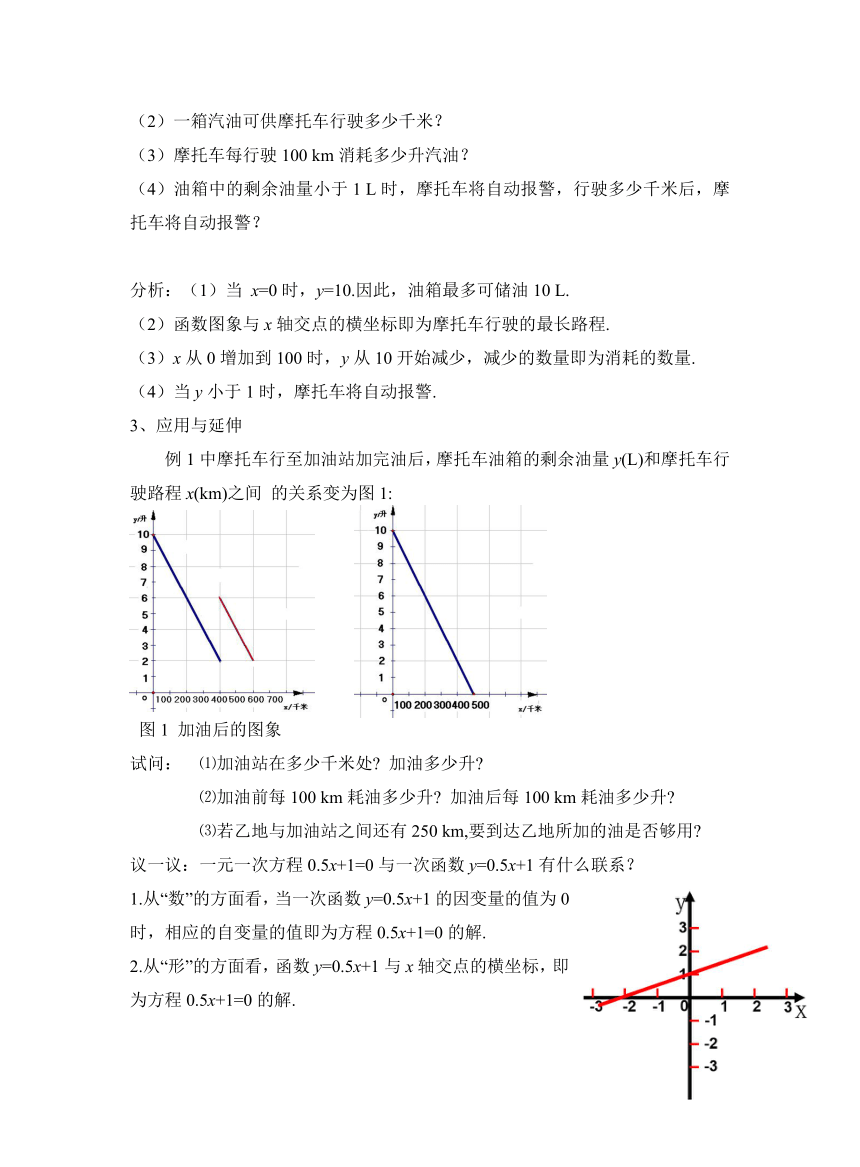
例1中摩托车行至加油站加完油后,摩托车油箱的剩余油量y(L)和摩托车行驶路程x(km)之间 的关系变为图1:
EMBED Paint.Picture \* MERGEFORMAT
图1 加油后的图象
试问: ⑴加油站在多少千米处 加油多少升
⑵加油前每100 km耗油多少升 加油后每100 km耗油多少升
⑶若乙地与加油站之间还有250 km,要到达乙地所加的油是否够用
议一议:一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系?
1.从“数”的方面看,当一次函数y=0.5x+1的因变量的值为0时,相应的自变量的值即为方程0.5x+1=0的解.
2.从“形”的方面看,函数y=0.5x+1与x轴交点的横坐标,即为方程0.5x+1=0的解.
练一练
1.直线y=2x+20与x轴交点坐标为(____,_____),这说明方程2x+20=0的解是x=_____.
2.若方程kx+b=0的解是x=5,则直线y=kx+b与x轴交点坐标为(____,_____).
归纳总结
例2 一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为( )
A.x=-1 B.x=2 C.x=0 D.x=3
【解析】由函数经过点(0,1)可得b=1,再将点(2,3)代入y=kx+1,可求出k的值为1,故一次函数的表达式为y=x+1,再求出方程x+1=0的解为x=-1.
方法总结:此题主要考查了一次函数与一元一次方程的关系,关键是正确利用待定系数法求出一次函数的关系式.
4、课堂练习
1.某地长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用y元与行李质量x kg的关系如图:
(1)旅客最多可免费携带多少千克行李?
⑵超过30 kg后,每千克需付多少元?
2. 全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源已经成为一项十分紧迫的任务,某地区现有土地100万平方千米,沙漠200万平方千米,土地沙漠化的变化情况如下图所示.
(1)如果不采取任何措施,那么到第5年底,该地区沙漠面积将增加多少万千米2?
(2)如果该地区沙漠的面积继续按此趋势扩大,那么从现在开始,第几年底后,该地区将丧失土地资源?
(3)如果从现在开始采取植树造林措施,每年改造4万千米2沙漠,那么到第几年底,该地区的沙漠面积能减少到176万千米2.
四、课堂小结
通过本节课的学习,你有什么收获
本节课主要学习了:
1.通过函数图象获取信息.
2.利用函数图象解决简单的实际问题.
3.初步体会方程与函数的关系.
4.利用函数图象解决简单的实际问题,关键是读图,关注图中横、纵坐标代表量.
【布置作业】
教材习题4.6.
五、板书设计
4 第2课时 一次函数图象的应用
1.根据图象求一次函数的表达式y=kx+b
2.利用函数图象解决简单实际问题的关键
3.方程与函数、直线之间的关系
六、教学反思
函数是描述客观世界变化规律的重要数学模型.用函数的观点处理实际问题的关键在于分析实际情境,建立函数模型,并进一步提出明确的数学问题,注意分析的过程,即将实际问题置于已有的知识背景之中,用数学知识重新理解这是什么或者可以看成什么,让学生逐步学会用数学的眼光考察实际问题.
原图
1
一、教学目标
1、能通过函数图象获取信息,发展形象思维.
2、能利用函数图象解决简单的实际问题,
3、初步体会方程与函数的关系.
二、教学重难点
重点:一次函数图象的应用.
难点:一元一次方程与一次函数的关系.
三、教学过程
1、新课导入
从一次函数图象可获得哪些信息
(1)由一次函数的图象可确定k 和 b 的符号;
(2)由一次函数的图象可估计函数的变化趋势;
(3)可直接观察出:x与y的对应值;
(4)由一次函数的图象与y轴的交点的坐标可确定b值,
从而确定一次函数的图象的表达式.
在前几节课里,我们分别学习了一次函数,一次函数的图象,一次函数图象的特征,并且了解到一次函数的应用十分广泛,和我们日常生活密切相关,因此本节课我们一起来学习一次函数图象的应用.
2、讲授新课
(1)由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少,干旱持续时间t(天)与蓄水量V(万米3)的关系如下图所示,回答下列问题:
①水库干旱前的蓄水量是多少?
②干旱持续10天,蓄水量为多少?连续干旱23天呢?
③蓄水量小于400万m3时,将发生严重干旱警报.干旱多少天后将发出严重干旱警报?
④按照这个规律,预计持续干旱多少天水库将干涸?
请大家根据图象回答问题,有困难的同学,请与同伴互相交流.
分析:
(1)1200万m3
(2)求干旱持续10天时的蓄水量,也就是求t等于10时所对应的V的值.当t=10时,V约为1000万m3。同理可知当t为23天时,V约为750万m3.
(3)当蓄水量小于400万m3时,将发出严重干旱警报,也就是当V等于400万m3时,求所对应的t值.t约为40天.
(4)水库干涸也就是V为0,所以求函数图象与横轴交点的横坐标即为所求.当V为0时,所对应的t的值约为60天.
例1 某种摩托车的油箱最多可储油10 L,加满油后,油箱中的剩余油量y(L)与摩托车行驶路程x (km)之间的关系如图所示.
根据图象回答下列问题:
(1)油箱最多可储油多少升?
(2)一箱汽油可供摩托车行驶多少千米?
(3)摩托车每行驶100 km消耗多少升汽油?
(4)油箱中的剩余油量小于1 L时,摩托车将自动报警,行驶多少千米后,摩托车将自动报警?
分析:(1)当 x=0时,y=10.因此,油箱最多可储油10 L.
(2)函数图象与x轴交点的横坐标即为摩托车行驶的最长路程.
(3)x从0增加到100时,y从10开始减少,减少的数量即为消耗的数量.
(4)当y小于1时,摩托车将自动报警.
3、应用与延伸
例1中摩托车行至加油站加完油后,摩托车油箱的剩余油量y(L)和摩托车行驶路程x(km)之间 的关系变为图1:
EMBED Paint.Picture \* MERGEFORMAT
图1 加油后的图象
试问: ⑴加油站在多少千米处 加油多少升
⑵加油前每100 km耗油多少升 加油后每100 km耗油多少升
⑶若乙地与加油站之间还有250 km,要到达乙地所加的油是否够用
议一议:一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系?
1.从“数”的方面看,当一次函数y=0.5x+1的因变量的值为0时,相应的自变量的值即为方程0.5x+1=0的解.
2.从“形”的方面看,函数y=0.5x+1与x轴交点的横坐标,即为方程0.5x+1=0的解.
练一练
1.直线y=2x+20与x轴交点坐标为(____,_____),这说明方程2x+20=0的解是x=_____.
2.若方程kx+b=0的解是x=5,则直线y=kx+b与x轴交点坐标为(____,_____).
归纳总结
例2 一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为( )
A.x=-1 B.x=2 C.x=0 D.x=3
【解析】由函数经过点(0,1)可得b=1,再将点(2,3)代入y=kx+1,可求出k的值为1,故一次函数的表达式为y=x+1,再求出方程x+1=0的解为x=-1.
方法总结:此题主要考查了一次函数与一元一次方程的关系,关键是正确利用待定系数法求出一次函数的关系式.
4、课堂练习
1.某地长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用y元与行李质量x kg的关系如图:
(1)旅客最多可免费携带多少千克行李?
⑵超过30 kg后,每千克需付多少元?
2. 全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源已经成为一项十分紧迫的任务,某地区现有土地100万平方千米,沙漠200万平方千米,土地沙漠化的变化情况如下图所示.
(1)如果不采取任何措施,那么到第5年底,该地区沙漠面积将增加多少万千米2?
(2)如果该地区沙漠的面积继续按此趋势扩大,那么从现在开始,第几年底后,该地区将丧失土地资源?
(3)如果从现在开始采取植树造林措施,每年改造4万千米2沙漠,那么到第几年底,该地区的沙漠面积能减少到176万千米2.
四、课堂小结
通过本节课的学习,你有什么收获
本节课主要学习了:
1.通过函数图象获取信息.
2.利用函数图象解决简单的实际问题.
3.初步体会方程与函数的关系.
4.利用函数图象解决简单的实际问题,关键是读图,关注图中横、纵坐标代表量.
【布置作业】
教材习题4.6.
五、板书设计
4 第2课时 一次函数图象的应用
1.根据图象求一次函数的表达式y=kx+b
2.利用函数图象解决简单实际问题的关键
3.方程与函数、直线之间的关系
六、教学反思
函数是描述客观世界变化规律的重要数学模型.用函数的观点处理实际问题的关键在于分析实际情境,建立函数模型,并进一步提出明确的数学问题,注意分析的过程,即将实际问题置于已有的知识背景之中,用数学知识重新理解这是什么或者可以看成什么,让学生逐步学会用数学的眼光考察实际问题.
原图
1
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
