5.2 运动的合成与分解 课件(16张PPT)高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 5.2 运动的合成与分解 课件(16张PPT)高一下学期物理人教版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-06 13:25:56 | ||
图片预览




文档简介
(共16张PPT)
运动的合成与分解
【学习目标】
1.通过对玻璃管内蜡块运动的分析,知道运动的合成与分解遵从的规律,理解合运动与分运动之间的关系,掌握不共线的两分运动合成后合运动性质的分析方法;
2.通过对“小猪佩奇一家过河野餐”的例题分析,让学生学会用运动的合成与分解来分析小船过河问题;
3.通过对“抛橄榄球”所做曲线运动的分析,学会“化曲为直”的思想方法;
3.通过“牵引车救援搁浅船”的情境分析,理解关联速度问题,并掌握其分析思路。
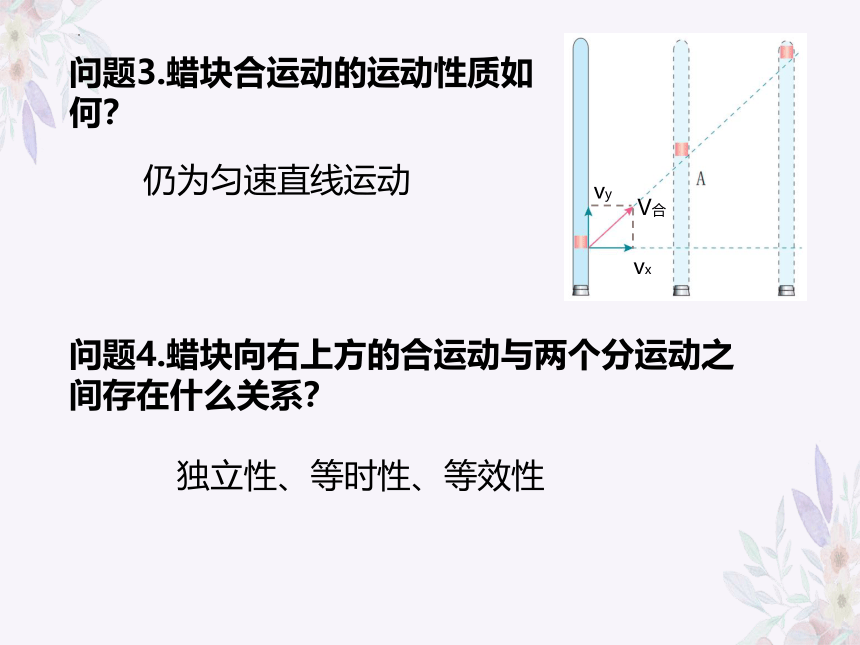
在一端封闭、长约1m的玻璃管内注入清水,水中放一个红蜡做的小圆柱体A,将玻璃管的开口端用橡胶塞塞紧。把玻璃管倒置,在蜡块A匀速上升的同时,将玻璃管贴着黑板沿水平方向向右匀速移动。
情境一
问题1.我们看到蜡块向右上方的运动由几部分构成?
问题2.什么是运动的合成与分解?运动的合成与分解遵从什么规律?
由沿着玻璃管向上的匀速直线运动和随着玻璃管向右的匀速直线运动共同构成。
由分运动求合运动的过程叫作运动的合成,由合运动求分运动的过程叫作运动的分解;
运动的合成与分解遵从矢量运算法则——平行四边形定则。
vx
vy
V合
问题3.蜡块合运动的运动性质如何?
仍为匀速直线运动
问题4.蜡块向右上方的合运动与两个分运动之间存在什么关系?
独立性、等时性、等效性
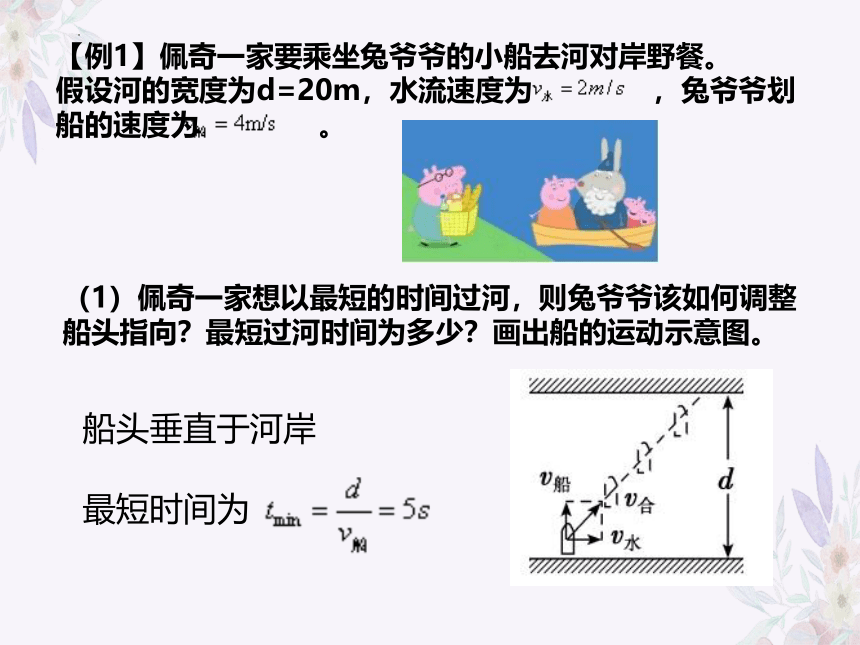
【例1】佩奇一家要乘坐兔爷爷的小船去河对岸野餐。
假设河的宽度为d=20m,水流速度为 ,兔爷爷划船的速度为 。
(1)佩奇一家想以最短的时间过河,则兔爷爷该如何调整船头指向?最短过河时间为多少?画出船的运动示意图。
船头垂直于河岸
最短时间为
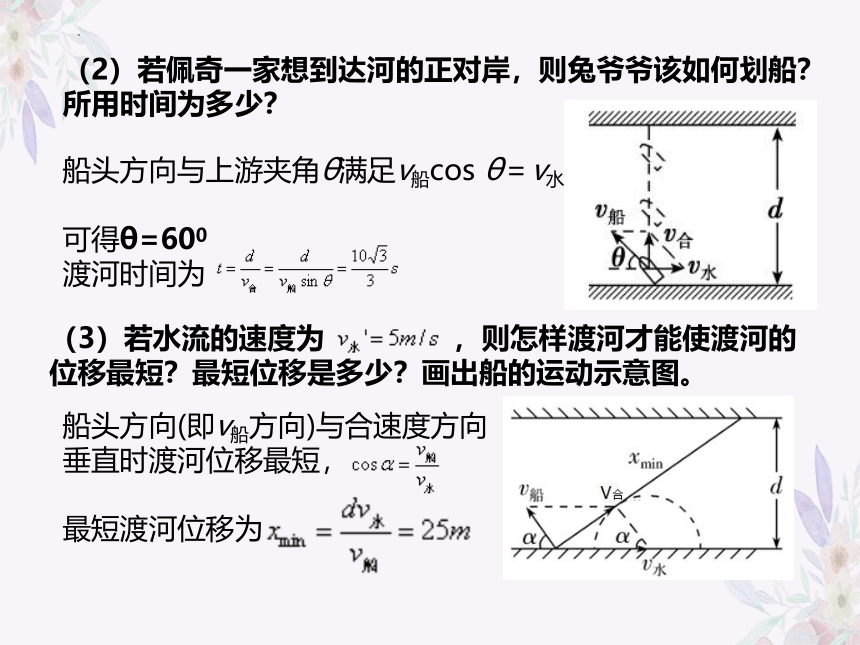
(2)若佩奇一家想到达河的正对岸,则兔爷爷该如何划船?所用时间为多少?
(3)若水流的速度为 ,则怎样渡河才能使渡河的位移最短?最短位移是多少?画出船的运动示意图。
船头方向与上游夹角θ满足v船cos θ=v水
可得θ=600
渡河时间为
船头方向(即v船方向)与合速度方向垂直时渡河位移最短,
最短渡河位移为
【针对训练1】(多选)雨滴由静止开始下落,遇到水平吹来的风,下列说法正确的是( )
A.风速越大,雨滴下落时间越长
B.风速越大,雨滴着地时速度越大
C.雨滴下落时间与风速无关
D.雨滴着地速度与风速无关
BC
独立性、等时性
情境二
对情境一,把玻璃管倒置后,在蜡块匀速上升的同时,若将玻璃管沿着x轴正方向做初速度为0的匀加速直线运动。请思考:
问题1.蜡块的实际运动由哪两个分运动构成?
由沿着玻璃管向上的匀速直线运动和随着玻璃管向右的匀加速直线运动共同构成
问题3.两个不共线的分运动合成后,如何判断合运动的运动性质?
问题2.蜡块合运动的性质如何?并在平面直角坐标系中大致画出蜡块的运动轨迹。
匀变速曲线运动
求出v合与a合
a合
恒定——匀变速
变化——变加速
v合与a合
共线——直线
不共线——曲线
【例2】 (多选)运动员在同一位置分别沿与地面成30°角和60°角的方向踢出一个橄榄球,两次球落在同一地点,运动轨迹如图所示,不计空气阻力,则橄榄球( )
AC
解决复杂曲线运动的基本思路——运动的分解
A.沿轨迹①运动时间长
B.沿轨迹②运动时间长
C.在最高点时沿轨迹②运动速度大
D.在最高点时沿轨迹①运动速度大
化曲为直
【针对训练2】质量为2 kg的质点在xOy平面上运动,t=0时刻质点在(0,6m)处,且x方向的速度—时间图象和y方向的位移—时间图象分别如图所示,则质点( )
A.初速度大小为4 m/s
B.所受合外力大小为4 N
C.做匀变速直线运动
D.初速度的方向与合外力的方向垂直
B
情境三
情境三:潮水退去后一艘游览船在海边搁浅,一辆救援牵引车通过跨过定滑轮的牵引绳将游览船拉到岸边,此救援过程的示意图如图所示。
问题1.搁浅船实际运动的速度方向如何?
问题2.绳拉着搁浅船运动时,救援牵引车与搁浅船的运动之间有什么联系?
问题3.当救援牵引车的速度为v,绳OA与水方向之间的夹角为θ时,牵引车与搁浅船的速度大小存在什么关系?
水平向左
沿着绳子方向的分速度大小相等
V船
V//
V┴
θ
【例3】曲柄连杆结构是发动机实现工作循环、完成能量转换的主要运动零件,如图所示,连杆下端连接活塞Q,上端连接曲轴P。在工作过程中,活塞在汽缸内上下运动,带动曲轴绕圆心O旋转,若P做线速度大小为v0的匀速圆周运动,则下列说法正确的是( )
A.当OP与OQ垂直时,活塞运动的速度等于v0
B.当OP与OQ垂直时,活塞运动的速度大于v0
C.当O、P、Q在同一直线上时,活塞运动的
速度等于v0
D.当O、P、Q在同一直线上时,活塞运动的
速度大于v0
A
【变式训练3】如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车以速度v匀速向右运动到图示位置时,物体P的速度为( )
A.v B.v cos θ
C. D.v cos2θ
B
V//
V┴
v
小结
1.运动的合成与分解遵从的规律
——平行四边形定则
2.合运动与分运动的关系
——独立性、等时性、等效性
3.两个不共线的运动的合运动性质的判断
4.关联速度问题
特点
解题思路
知识
方法
解决复杂曲线运动问题的基本方法
——运动的分解
化曲为直
运动的合成与分解
【学习目标】
1.通过对玻璃管内蜡块运动的分析,知道运动的合成与分解遵从的规律,理解合运动与分运动之间的关系,掌握不共线的两分运动合成后合运动性质的分析方法;
2.通过对“小猪佩奇一家过河野餐”的例题分析,让学生学会用运动的合成与分解来分析小船过河问题;
3.通过对“抛橄榄球”所做曲线运动的分析,学会“化曲为直”的思想方法;
3.通过“牵引车救援搁浅船”的情境分析,理解关联速度问题,并掌握其分析思路。
在一端封闭、长约1m的玻璃管内注入清水,水中放一个红蜡做的小圆柱体A,将玻璃管的开口端用橡胶塞塞紧。把玻璃管倒置,在蜡块A匀速上升的同时,将玻璃管贴着黑板沿水平方向向右匀速移动。
情境一
问题1.我们看到蜡块向右上方的运动由几部分构成?
问题2.什么是运动的合成与分解?运动的合成与分解遵从什么规律?
由沿着玻璃管向上的匀速直线运动和随着玻璃管向右的匀速直线运动共同构成。
由分运动求合运动的过程叫作运动的合成,由合运动求分运动的过程叫作运动的分解;
运动的合成与分解遵从矢量运算法则——平行四边形定则。
vx
vy
V合
问题3.蜡块合运动的运动性质如何?
仍为匀速直线运动
问题4.蜡块向右上方的合运动与两个分运动之间存在什么关系?
独立性、等时性、等效性
【例1】佩奇一家要乘坐兔爷爷的小船去河对岸野餐。
假设河的宽度为d=20m,水流速度为 ,兔爷爷划船的速度为 。
(1)佩奇一家想以最短的时间过河,则兔爷爷该如何调整船头指向?最短过河时间为多少?画出船的运动示意图。
船头垂直于河岸
最短时间为
(2)若佩奇一家想到达河的正对岸,则兔爷爷该如何划船?所用时间为多少?
(3)若水流的速度为 ,则怎样渡河才能使渡河的位移最短?最短位移是多少?画出船的运动示意图。
船头方向与上游夹角θ满足v船cos θ=v水
可得θ=600
渡河时间为
船头方向(即v船方向)与合速度方向垂直时渡河位移最短,
最短渡河位移为
【针对训练1】(多选)雨滴由静止开始下落,遇到水平吹来的风,下列说法正确的是( )
A.风速越大,雨滴下落时间越长
B.风速越大,雨滴着地时速度越大
C.雨滴下落时间与风速无关
D.雨滴着地速度与风速无关
BC
独立性、等时性
情境二
对情境一,把玻璃管倒置后,在蜡块匀速上升的同时,若将玻璃管沿着x轴正方向做初速度为0的匀加速直线运动。请思考:
问题1.蜡块的实际运动由哪两个分运动构成?
由沿着玻璃管向上的匀速直线运动和随着玻璃管向右的匀加速直线运动共同构成
问题3.两个不共线的分运动合成后,如何判断合运动的运动性质?
问题2.蜡块合运动的性质如何?并在平面直角坐标系中大致画出蜡块的运动轨迹。
匀变速曲线运动
求出v合与a合
a合
恒定——匀变速
变化——变加速
v合与a合
共线——直线
不共线——曲线
【例2】 (多选)运动员在同一位置分别沿与地面成30°角和60°角的方向踢出一个橄榄球,两次球落在同一地点,运动轨迹如图所示,不计空气阻力,则橄榄球( )
AC
解决复杂曲线运动的基本思路——运动的分解
A.沿轨迹①运动时间长
B.沿轨迹②运动时间长
C.在最高点时沿轨迹②运动速度大
D.在最高点时沿轨迹①运动速度大
化曲为直
【针对训练2】质量为2 kg的质点在xOy平面上运动,t=0时刻质点在(0,6m)处,且x方向的速度—时间图象和y方向的位移—时间图象分别如图所示,则质点( )
A.初速度大小为4 m/s
B.所受合外力大小为4 N
C.做匀变速直线运动
D.初速度的方向与合外力的方向垂直
B
情境三
情境三:潮水退去后一艘游览船在海边搁浅,一辆救援牵引车通过跨过定滑轮的牵引绳将游览船拉到岸边,此救援过程的示意图如图所示。
问题1.搁浅船实际运动的速度方向如何?
问题2.绳拉着搁浅船运动时,救援牵引车与搁浅船的运动之间有什么联系?
问题3.当救援牵引车的速度为v,绳OA与水方向之间的夹角为θ时,牵引车与搁浅船的速度大小存在什么关系?
水平向左
沿着绳子方向的分速度大小相等
V船
V//
V┴
θ
【例3】曲柄连杆结构是发动机实现工作循环、完成能量转换的主要运动零件,如图所示,连杆下端连接活塞Q,上端连接曲轴P。在工作过程中,活塞在汽缸内上下运动,带动曲轴绕圆心O旋转,若P做线速度大小为v0的匀速圆周运动,则下列说法正确的是( )
A.当OP与OQ垂直时,活塞运动的速度等于v0
B.当OP与OQ垂直时,活塞运动的速度大于v0
C.当O、P、Q在同一直线上时,活塞运动的
速度等于v0
D.当O、P、Q在同一直线上时,活塞运动的
速度大于v0
A
【变式训练3】如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车以速度v匀速向右运动到图示位置时,物体P的速度为( )
A.v B.v cos θ
C. D.v cos2θ
B
V//
V┴
v
小结
1.运动的合成与分解遵从的规律
——平行四边形定则
2.合运动与分运动的关系
——独立性、等时性、等效性
3.两个不共线的运动的合运动性质的判断
4.关联速度问题
特点
解题思路
知识
方法
解决复杂曲线运动问题的基本方法
——运动的分解
化曲为直
