初中数学北师大版九上1.2.1矩形的性质 教案
文档属性
| 名称 | 初中数学北师大版九上1.2.1矩形的性质 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 241.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 13:53:06 | ||
图片预览



文档简介
1.2.1矩形的性质
一、教学目标
1.理解矩形的概念、矩形与平行四边形的区别与联系.(重点)
2.会证明矩形的性质并解决相关问题.(重点、难点)
3.掌握直角三角形斜边中线的性质,并会运用(重点)
一、教学重难点:
1.理解矩形的概念、矩形与平行四边形的区别与联系.(重点)
2.会证明矩形的性质并解决相关问题.(重点、难点)
3.掌握直角三角形斜边中线的性质,并会运用(重点)
三、 教学方法:
探究法、讲授法
四、教学过程
(一)创设情境 新课导入
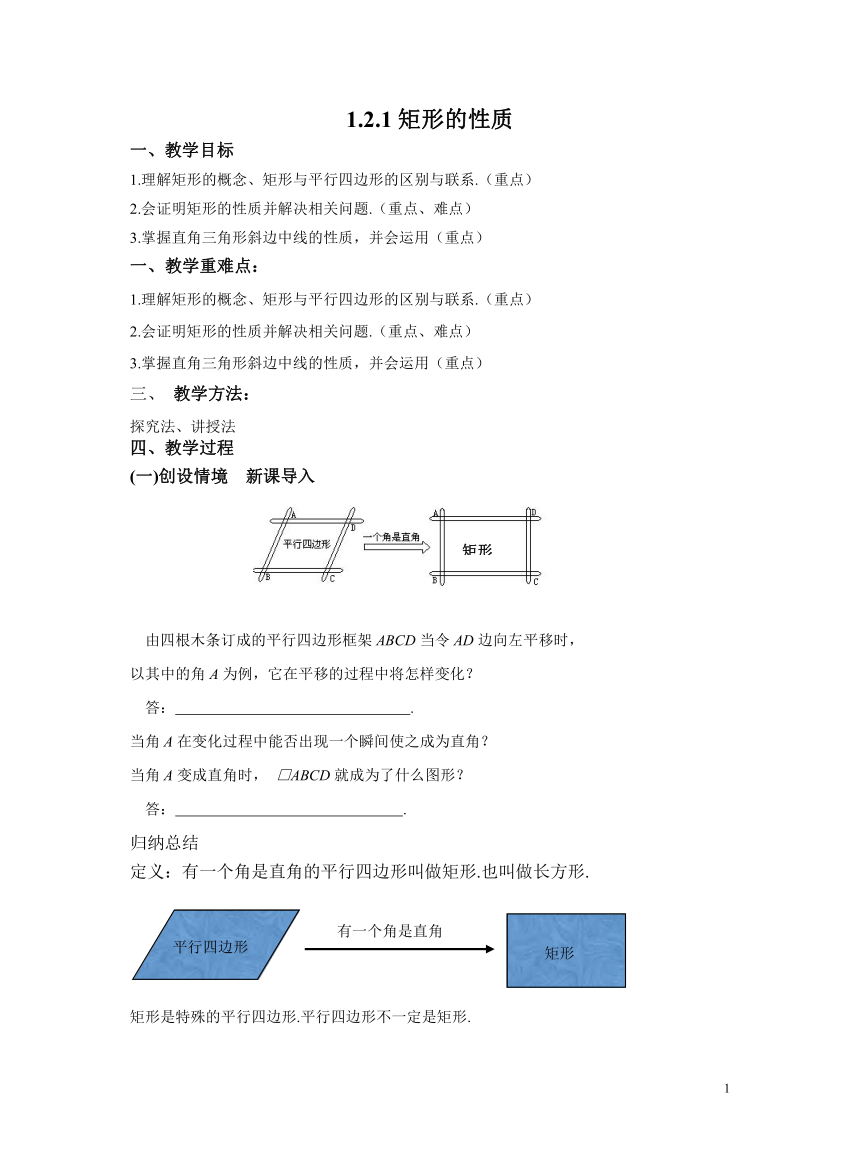
由四根木条订成的平行四边形框架ABCD当令AD边向左平移时,
以其中的角A为例,它在平移的过程中将怎样变化?
答: .
当角A在变化过程中能否出现一个瞬间使之成为直角?
当角A变成直角时, □ABCD就成为了什么图形?
答: .
归纳总结
定义:有一个角是直角的平行四边形叫做矩形.也叫做长方形.
矩形是特殊的平行四边形.平行四边形不一定是矩形.
、新课讲授
一、矩形的性质
矩形定义: 的平行四边形叫 .
根据定义知道:矩形是平行四边形,具有平行四边形的所有性质.
矩形又是特殊的平行四边形,是否具有一般平行四边形不具有的一些特殊性质?
猜想1:矩形的四个内角都是直角
猜想2:矩形的对角线相等
证明猜想1:如图1.2.1-1,四边形ABCD是矩形,∠B=90°.
求证: ∠B=∠C=∠D=∠A=90°.
证明猜想2:如图1.2.1-2,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相较于点O.
求证:AC=DB.
归纳总结:
文字语言 图形语言 几何语言描述:
矩形的四个角都是直角.矩形的对角线相等. 在矩形ABCD中,对角线AC与DB相交于点O.∠ABC=∠BCD=∠CDA=∠DAB =90°,AC=DB.
(三)、例题讲解
例1 已知:如上图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4,求矩形对角线的长.
例2 如图,在矩形ABCD中,E是BC上一点AE=AD,DF⊥AE,垂足为F.
求证:DF=DC.
例3 如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,求△BED的面积.
思考 请同学们拿出准备好的矩形纸片,折一折,观察并思考. 矩形是不是轴对称图形 如果是,那么对称轴有几条
目标检测一
1.如图,在矩形ABCD中,对角线AC,BD交于点O, 下列说法错误的是 ( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OB
2.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的_________.
3.如图,在矩形ABCD中,AE⊥BD于E,∠DAE:∠BAE=3:1,求∠BAE和∠EAO的度数.
二、直角三角形斜边上的中线的性质
活动:如图,一张矩形纸片,画出两条对角线,沿着对角线AC剪去一半.
问题 Rt△ABC中,BO是一条怎样的线段?它的长度与斜边AC有什么关系?
猜想:直角三角形斜边上的中线等于斜边的一半.
证明猜想:如图,在Rt△ABC中,∠ABC=90°,BO是AC上的中线.求证: BO = AC
例4 如图1.2.1-5,在△ABC中,AD是高,E、F分别是AB、AC的中点.
若AB=10,AC=8,求四边形AEDF的周长;
(2)求证:EF垂直平分AD.
例5 如图1.2.1-6,已知BD,CE是△ABC不同边上的高,点G,F分别是BC,DE的中点,试说明GF⊥DE.
目标检测二
如图,在△ABC中,∠ABC = 90°,BD是斜边AC上的中线.
(1)若BD=3 cm,则AC =_____cm;
(2)若∠C = 30°,AB = 5 cm,则AC =_____cm,BD = _____cm.
目标检测三
1.矩形具有而一般平行四边形不具有的性质是 ( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
3.若矩形的一条对角线与一边的夹角为40°,则两条对角线相交的锐角是 ( )
A.20 ° B.40° C.80 ° D.10°
4、如图1.2.1-7,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
5.如图,△ABC中,E在AC上,且BE⊥AC.D为AB中点,若DE=5,AE=8,则BE的长为______.
如图1.2.1-8,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,求PE+PF的值
(五)课堂小结
菱形定义:有一个角是直角的平行四边形是矩形.
菱形的性质1:矩形的四个角都是直角.
菱形的性质2:矩形的对角线相等.
(六)作业布置
完成本课时课后跟踪练习
五、板书设计
矩形
平行四边形
矩形
有一个角是直角
D
A
1.2.1-1
B
C
B
C
D
O
A
1.2.1-2
0
C
B
A
D
C
B
A
D
O
A
B
C
D
O
B
C
O
A
C
B
A
D
O
1.2.1-5
1.2.1-6
1
一、教学目标
1.理解矩形的概念、矩形与平行四边形的区别与联系.(重点)
2.会证明矩形的性质并解决相关问题.(重点、难点)
3.掌握直角三角形斜边中线的性质,并会运用(重点)
一、教学重难点:
1.理解矩形的概念、矩形与平行四边形的区别与联系.(重点)
2.会证明矩形的性质并解决相关问题.(重点、难点)
3.掌握直角三角形斜边中线的性质,并会运用(重点)
三、 教学方法:
探究法、讲授法
四、教学过程
(一)创设情境 新课导入
由四根木条订成的平行四边形框架ABCD当令AD边向左平移时,
以其中的角A为例,它在平移的过程中将怎样变化?
答: .
当角A在变化过程中能否出现一个瞬间使之成为直角?
当角A变成直角时, □ABCD就成为了什么图形?
答: .
归纳总结
定义:有一个角是直角的平行四边形叫做矩形.也叫做长方形.
矩形是特殊的平行四边形.平行四边形不一定是矩形.
、新课讲授
一、矩形的性质
矩形定义: 的平行四边形叫 .
根据定义知道:矩形是平行四边形,具有平行四边形的所有性质.
矩形又是特殊的平行四边形,是否具有一般平行四边形不具有的一些特殊性质?
猜想1:矩形的四个内角都是直角
猜想2:矩形的对角线相等
证明猜想1:如图1.2.1-1,四边形ABCD是矩形,∠B=90°.
求证: ∠B=∠C=∠D=∠A=90°.
证明猜想2:如图1.2.1-2,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相较于点O.
求证:AC=DB.
归纳总结:
文字语言 图形语言 几何语言描述:
矩形的四个角都是直角.矩形的对角线相等. 在矩形ABCD中,对角线AC与DB相交于点O.∠ABC=∠BCD=∠CDA=∠DAB =90°,AC=DB.
(三)、例题讲解
例1 已知:如上图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4,求矩形对角线的长.
例2 如图,在矩形ABCD中,E是BC上一点AE=AD,DF⊥AE,垂足为F.
求证:DF=DC.
例3 如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,求△BED的面积.
思考 请同学们拿出准备好的矩形纸片,折一折,观察并思考. 矩形是不是轴对称图形 如果是,那么对称轴有几条
目标检测一
1.如图,在矩形ABCD中,对角线AC,BD交于点O, 下列说法错误的是 ( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OB
2.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD面积的_________.
3.如图,在矩形ABCD中,AE⊥BD于E,∠DAE:∠BAE=3:1,求∠BAE和∠EAO的度数.
二、直角三角形斜边上的中线的性质
活动:如图,一张矩形纸片,画出两条对角线,沿着对角线AC剪去一半.
问题 Rt△ABC中,BO是一条怎样的线段?它的长度与斜边AC有什么关系?
猜想:直角三角形斜边上的中线等于斜边的一半.
证明猜想:如图,在Rt△ABC中,∠ABC=90°,BO是AC上的中线.求证: BO = AC
例4 如图1.2.1-5,在△ABC中,AD是高,E、F分别是AB、AC的中点.
若AB=10,AC=8,求四边形AEDF的周长;
(2)求证:EF垂直平分AD.
例5 如图1.2.1-6,已知BD,CE是△ABC不同边上的高,点G,F分别是BC,DE的中点,试说明GF⊥DE.
目标检测二
如图,在△ABC中,∠ABC = 90°,BD是斜边AC上的中线.
(1)若BD=3 cm,则AC =_____cm;
(2)若∠C = 30°,AB = 5 cm,则AC =_____cm,BD = _____cm.
目标检测三
1.矩形具有而一般平行四边形不具有的性质是 ( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
2.若直角三角形的两条直角边分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
3.若矩形的一条对角线与一边的夹角为40°,则两条对角线相交的锐角是 ( )
A.20 ° B.40° C.80 ° D.10°
4、如图1.2.1-7,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
5.如图,△ABC中,E在AC上,且BE⊥AC.D为AB中点,若DE=5,AE=8,则BE的长为______.
如图1.2.1-8,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,求PE+PF的值
(五)课堂小结
菱形定义:有一个角是直角的平行四边形是矩形.
菱形的性质1:矩形的四个角都是直角.
菱形的性质2:矩形的对角线相等.
(六)作业布置
完成本课时课后跟踪练习
五、板书设计
矩形
平行四边形
矩形
有一个角是直角
D
A
1.2.1-1
B
C
B
C
D
O
A
1.2.1-2
0
C
B
A
D
C
B
A
D
O
A
B
C
D
O
B
C
O
A
C
B
A
D
O
1.2.1-5
1.2.1-6
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
