初中数学北师大版七上教案5.6应用一元一次方程——追赶小明
文档属性
| 名称 | 初中数学北师大版七上教案5.6应用一元一次方程——追赶小明 |

|
|
| 格式 | doc | ||
| 文件大小 | 174.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 00:00:00 | ||
图片预览

文档简介
5.6 应用一元一次方程——追赶小明
一、教学目标
1.能分析行程问题中已知数与未知数之间的数量关系,利用路程、时间与速度三个量之间的关系式,列出一元一次方程解应用题.
2.会用“线段图”分析复杂问题中的数量关系,从而建立方程解决实际问题,培养分析问题、解决问题的能力,进一步体会方程模型的作用.
二、教学重难点
【重点】学会利用线段图分析行程问题,寻找等量关系,建立数学模型.
【难点】能利用行程中的速度、路程、时间之间的关系列方程解应用题.
三、教学方法
探究法、归纳总结法
四、教学过程
(一)新课导入
亲爱的同学们,你们读过名著《西游记》吗?关于孙悟空的故事你一定知道很多吧.有这样一首描述孙悟空捉妖的诗:悟空顺风探妖踪,千里只用四分钟;归时四分行六百,风速多少才算准.请你帮孙悟空算算当时的风速每分钟是多少里?
(二)新课讲授
探究点一:用一元一次方程解决相遇问题
小明家离学校2.9 km,一天小明放学走了5 min之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60 m,爸爸骑自行车每分钟骑200 m,请问小明爸爸从家出发几分钟后接到小明?
解析:本题等量关系:小明所走的路程+爸爸所走的路程=全部路程,但要注意小明比爸爸多走了5分钟,所以小明所走的时间为(x+5)分钟,另外也要注意本题单位的统一.
解:设小明爸爸出发x分钟后接到小明,如图所示,由题意,得200x+60(x+5)=2900.解得x=10.
答:小明爸爸从家出发10分钟后接到小明.
方法总结:找出问题中的等量关系是列方程解应用题的关键,对于行程问题,通常借助“线段图”来分析问题中的数量关系. 这样可以比较直观地反映出方程中的等量关系.
两人从两地出发相向而行的行程问题称为相遇问题.
往往根据路程之和等于总路程列方程.如图所示,甲的行程+乙的行程=两地距离.
探究点二:用一元一次方程解决追及问题
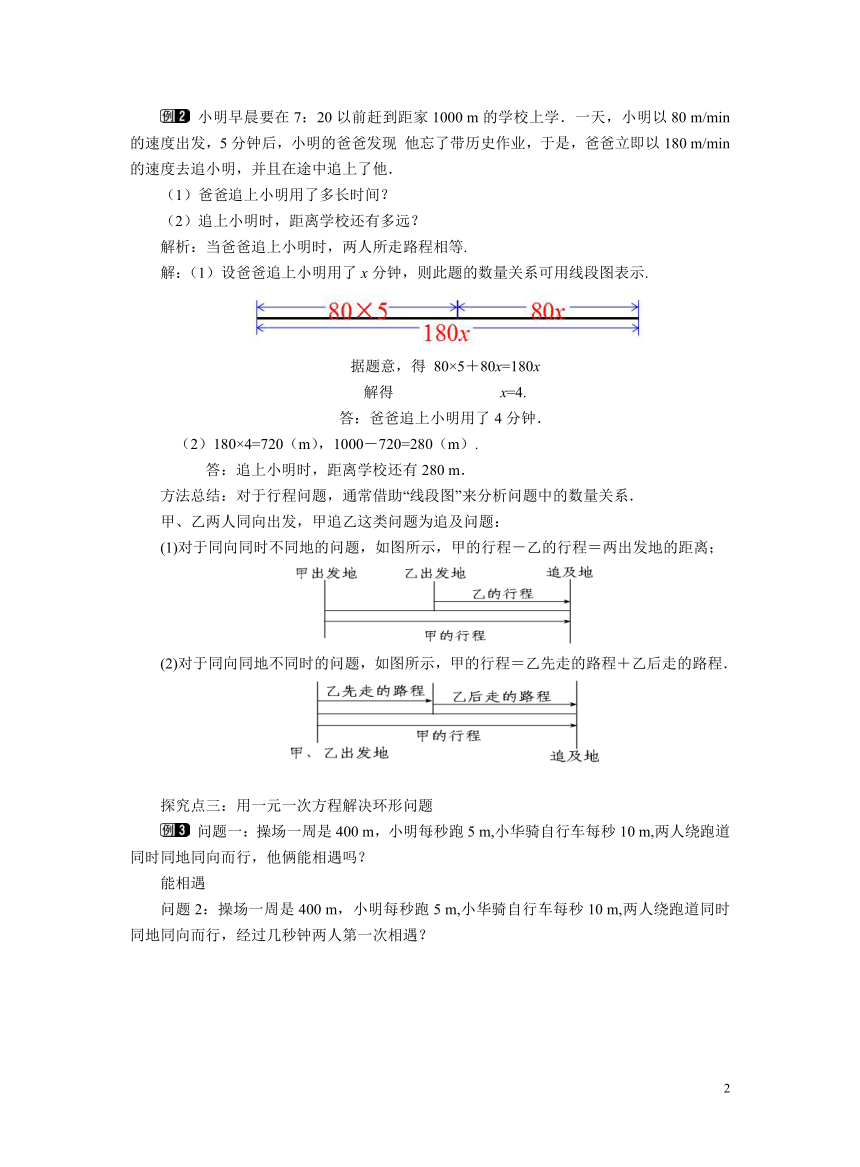
小明早晨要在7:20以前赶到距家1000 m的学校上学.一天,小明以80 m/min的速度出发,5分钟后,小明的爸爸发现 他忘了带历史作业,于是,爸爸立即以180 m/min的速度去追小明,并且在途中追上了他.
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
解析:当爸爸追上小明时,两人所走路程相等.
解:(1)设爸爸追上小明用了x分钟,则此题的数量关系可用线段图表示.
据题意,得 80×5+80x=180x
解得 x=4.
答:爸爸追上小明用了4分钟.
(2)180×4=720(m),1000-720=280(m).
答:追上小明时,距离学校还有280 m.
方法总结:对于行程问题,通常借助“线段图”来分析问题中的数量关系.
甲、乙两人同向出发,甲追乙这类问题为追及问题:
(1)对于同向同时不同地的问题,如图所示,甲的行程-乙的行程=两出发地的距离;
(2)对于同向同地不同时的问题,如图所示,甲的行程=乙先走的路程+乙后走的路程.
探究点三:用一元一次方程解决环形问题
问题一:操场一周是400 m,小明每秒跑5 m,小华骑自行车每秒10 m,两人绕跑道同时同地同向而行,他俩能相遇吗?
能相遇
问题2:操场一周是400 m,小明每秒跑5 m,小华骑自行车每秒10 m,两人绕跑道同时同地同向而行,经过几秒钟两人第一次相遇?
方法总结:环形问题中的相等关系:两个人同地背向而行:相遇问题(首次相遇),甲的行程+乙的行程=一圈周长;两个人同地同向而行:追及问题(首次追上),甲的行程-乙的行程=一圈周长.
(三)课堂练习
1.甲、乙两人练习赛跑,甲每秒跑4 m,乙每秒跑6 m,甲先跑10 s,乙开始跑,设乙x秒后追上甲,依题意列方程得( B )
A. 6x =4x B. 6x=4x+40 C. 6x= 4x-40 D. 4x+10=6
2.甲车在乙车前500 km,同时出发,速度分别为每小时40 km和每小时60 km,多少小时后,乙车追上甲车?设x小时后乙车追上甲车,则下面所列方程正确的是( C )
A.60x=500 B.60x=40x-500 C.60x=40x+500 D.40x=500
3.甲、乙两站间的距离为450 km,一列慢车从甲站开出,每小时行驶65 km,一列快车从乙站开出,每小时行驶85 km.设两车同时开出,同向而行,则快车几小时后追上慢车?其等量关系式是 :
答案:快车的路程=慢车的路程+甲、乙两站间的距离
4.A、B两地相距27 km,甲、乙两人分别从A、B两地同时出发,相向而行.已知甲的速度为4 km/h,乙的速度为5 km/h,则甲、乙两人___小时后相遇.
答案:3
5.敌我两军相距25 km,敌军以5 km/h的速度逃跑,我军同时以8 km/h的速度追击,并在相距1 km处发生战斗,问战斗是在开始追击后几小时发生的?
解:设战斗是在开始追击后x小时发生的.
根据题意,得 8x-5x=25-1.
解得 x=8.
答:战斗是在开始追击后8小时发生的.
(四)课堂小结
1.会借线段图分析行程问题.
2.各种行程问题中的规律及等量关系.
同向追及问题:
①同时不同地——甲路程+路程差=乙路程; 甲时间=乙时间.
②同地不同时——甲时间+时间差=乙时间; 甲路程=乙路程.
相向的相遇问题:
甲路程+乙路程=总路程; 甲时间=乙时间.
环形跑道问题:
设v甲>v乙,环形跑道长s m,经过t s甲、乙第一次相遇.
一般有如下两种情形:
①同时同地、同向而行:v甲t-v乙t=s.
②同时同地、背向而行:v甲t+v乙t=s.
(五)作业布置
完成教材第151页习题
五、板书设计
追赶小明→行程问题→
1
一、教学目标
1.能分析行程问题中已知数与未知数之间的数量关系,利用路程、时间与速度三个量之间的关系式,列出一元一次方程解应用题.
2.会用“线段图”分析复杂问题中的数量关系,从而建立方程解决实际问题,培养分析问题、解决问题的能力,进一步体会方程模型的作用.
二、教学重难点
【重点】学会利用线段图分析行程问题,寻找等量关系,建立数学模型.
【难点】能利用行程中的速度、路程、时间之间的关系列方程解应用题.
三、教学方法
探究法、归纳总结法
四、教学过程
(一)新课导入
亲爱的同学们,你们读过名著《西游记》吗?关于孙悟空的故事你一定知道很多吧.有这样一首描述孙悟空捉妖的诗:悟空顺风探妖踪,千里只用四分钟;归时四分行六百,风速多少才算准.请你帮孙悟空算算当时的风速每分钟是多少里?
(二)新课讲授
探究点一:用一元一次方程解决相遇问题
小明家离学校2.9 km,一天小明放学走了5 min之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60 m,爸爸骑自行车每分钟骑200 m,请问小明爸爸从家出发几分钟后接到小明?
解析:本题等量关系:小明所走的路程+爸爸所走的路程=全部路程,但要注意小明比爸爸多走了5分钟,所以小明所走的时间为(x+5)分钟,另外也要注意本题单位的统一.
解:设小明爸爸出发x分钟后接到小明,如图所示,由题意,得200x+60(x+5)=2900.解得x=10.
答:小明爸爸从家出发10分钟后接到小明.
方法总结:找出问题中的等量关系是列方程解应用题的关键,对于行程问题,通常借助“线段图”来分析问题中的数量关系. 这样可以比较直观地反映出方程中的等量关系.
两人从两地出发相向而行的行程问题称为相遇问题.
往往根据路程之和等于总路程列方程.如图所示,甲的行程+乙的行程=两地距离.
探究点二:用一元一次方程解决追及问题
小明早晨要在7:20以前赶到距家1000 m的学校上学.一天,小明以80 m/min的速度出发,5分钟后,小明的爸爸发现 他忘了带历史作业,于是,爸爸立即以180 m/min的速度去追小明,并且在途中追上了他.
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
解析:当爸爸追上小明时,两人所走路程相等.
解:(1)设爸爸追上小明用了x分钟,则此题的数量关系可用线段图表示.
据题意,得 80×5+80x=180x
解得 x=4.
答:爸爸追上小明用了4分钟.
(2)180×4=720(m),1000-720=280(m).
答:追上小明时,距离学校还有280 m.
方法总结:对于行程问题,通常借助“线段图”来分析问题中的数量关系.
甲、乙两人同向出发,甲追乙这类问题为追及问题:
(1)对于同向同时不同地的问题,如图所示,甲的行程-乙的行程=两出发地的距离;
(2)对于同向同地不同时的问题,如图所示,甲的行程=乙先走的路程+乙后走的路程.
探究点三:用一元一次方程解决环形问题
问题一:操场一周是400 m,小明每秒跑5 m,小华骑自行车每秒10 m,两人绕跑道同时同地同向而行,他俩能相遇吗?
能相遇
问题2:操场一周是400 m,小明每秒跑5 m,小华骑自行车每秒10 m,两人绕跑道同时同地同向而行,经过几秒钟两人第一次相遇?
方法总结:环形问题中的相等关系:两个人同地背向而行:相遇问题(首次相遇),甲的行程+乙的行程=一圈周长;两个人同地同向而行:追及问题(首次追上),甲的行程-乙的行程=一圈周长.
(三)课堂练习
1.甲、乙两人练习赛跑,甲每秒跑4 m,乙每秒跑6 m,甲先跑10 s,乙开始跑,设乙x秒后追上甲,依题意列方程得( B )
A. 6x =4x B. 6x=4x+40 C. 6x= 4x-40 D. 4x+10=6
2.甲车在乙车前500 km,同时出发,速度分别为每小时40 km和每小时60 km,多少小时后,乙车追上甲车?设x小时后乙车追上甲车,则下面所列方程正确的是( C )
A.60x=500 B.60x=40x-500 C.60x=40x+500 D.40x=500
3.甲、乙两站间的距离为450 km,一列慢车从甲站开出,每小时行驶65 km,一列快车从乙站开出,每小时行驶85 km.设两车同时开出,同向而行,则快车几小时后追上慢车?其等量关系式是 :
答案:快车的路程=慢车的路程+甲、乙两站间的距离
4.A、B两地相距27 km,甲、乙两人分别从A、B两地同时出发,相向而行.已知甲的速度为4 km/h,乙的速度为5 km/h,则甲、乙两人___小时后相遇.
答案:3
5.敌我两军相距25 km,敌军以5 km/h的速度逃跑,我军同时以8 km/h的速度追击,并在相距1 km处发生战斗,问战斗是在开始追击后几小时发生的?
解:设战斗是在开始追击后x小时发生的.
根据题意,得 8x-5x=25-1.
解得 x=8.
答:战斗是在开始追击后8小时发生的.
(四)课堂小结
1.会借线段图分析行程问题.
2.各种行程问题中的规律及等量关系.
同向追及问题:
①同时不同地——甲路程+路程差=乙路程; 甲时间=乙时间.
②同地不同时——甲时间+时间差=乙时间; 甲路程=乙路程.
相向的相遇问题:
甲路程+乙路程=总路程; 甲时间=乙时间.
环形跑道问题:
设v甲>v乙,环形跑道长s m,经过t s甲、乙第一次相遇.
一般有如下两种情形:
①同时同地、同向而行:v甲t-v乙t=s.
②同时同地、背向而行:v甲t+v乙t=s.
(五)作业布置
完成教材第151页习题
五、板书设计
追赶小明→行程问题→
1
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
