初中数学人教版九下29.1投影(第2课时) 教案
文档属性
| 名称 | 初中数学人教版九下29.1投影(第2课时) 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 820.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 14:36:20 | ||
图片预览

文档简介
29.1投影
(第2课时)
一、教学内容分析
正投影是建立在平行投影基础上的,是对平行投影知识的延伸.同时,正投影也是后续学习视图知识的基础,由此形成了“投影——平行投影——正投影——视图”的知识链条.由于正投影是在三维空间中进行研究的,所以不可避免的涉及到一些空间图形的位置关系,比如空间中的两条直线平行、直线与平面的平行、斜交与垂直等,对此借助实际物体进行直观描述说明即可.
二、教学目标
1.结合实例,了解正投影的概念,进一步了解投影的意义.
2.根据正投影的性质画出简单几何体的正投影.
3.通过探索几何体及其正投影的关系,体会立体图形与平面图形的相互转化,发展空间观念.
三、教学重难点
【重点】结合具体实例了解正投影的概念和性质.
【难点】画出简单几何体的正投影.
四、教学方法
演示法.由于初中学生接触的主要是平面内一维或二维的几何图形,对于三维空间内的图形认识有限,所以可以借助真实的几何体进行演示,让学生直观感知正投影的形成,并观察其特征.
五、教学过程
(一)新课导入
复习:
1.形成投影有哪些要素?
2.根据投影线(或光源)特征,可以把投影分为哪几种类型?举例说明.
演示:把一块三角板放在一张硬纸板的正上方,使三角板与硬纸板平行,分别在上面用灯泡照射、阳光斜射、阳光直射三种方式,如图所示.
图1 图2 图3
思考:
1.三个演示中的光源、投影线、投影面、投影分别是什么?
2.三个投影中,哪个是中心投影?哪个是平行投影?为什么?
3.平行投影中的投影线与投影面有什么位置关系?
【提示】图1投影线集中于一点,故为中心投影;
图2与图3中投影线互相平行,故为平行投影;
图2中,投影线斜着照射投影面;
图3中投影线垂直照射投影面(即投影线正对着投影面),我们也称这种情形为投影线垂直于投影面.
意图:复习上节课所学的知识,为学习正投影做好铺垫,并顺利导入新课.
(二)新课讲授
活动一 学习正投影的概念
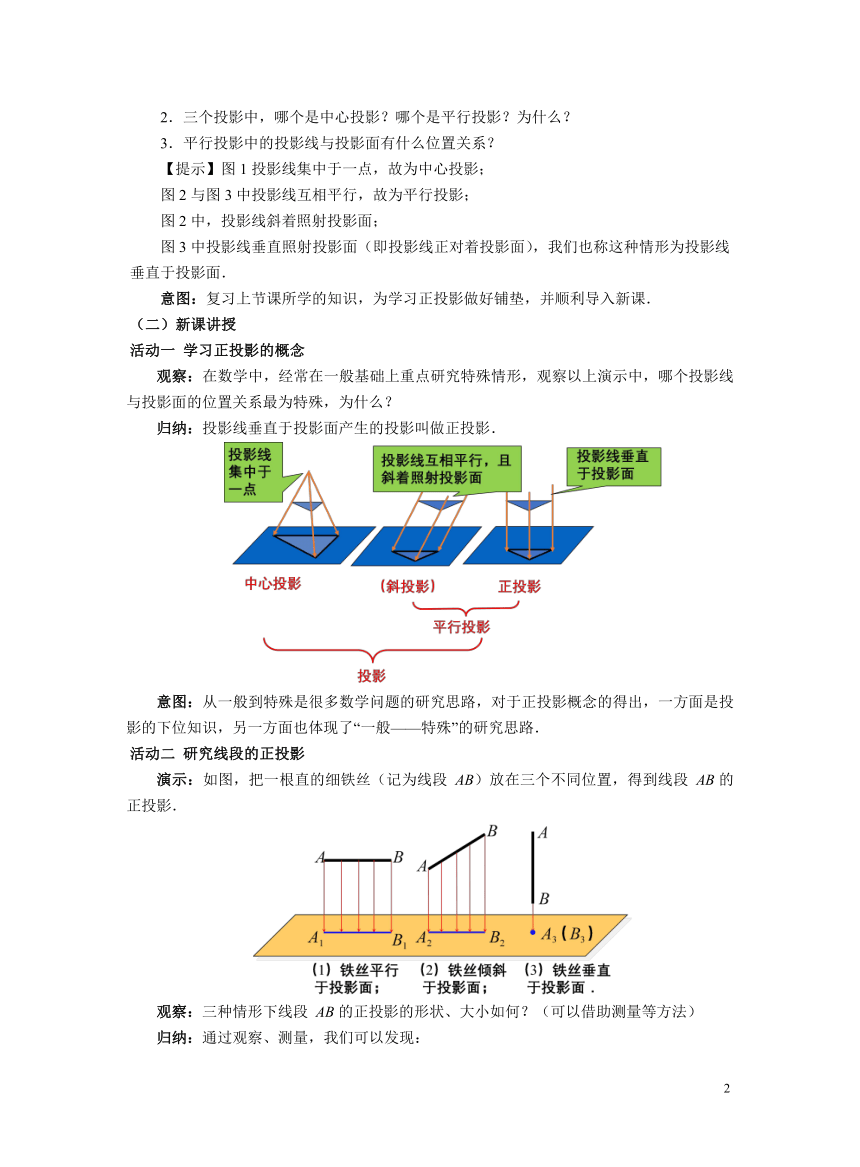
观察:在数学中,经常在一般基础上重点研究特殊情形,观察以上演示中,哪个投影线与投影面的位置关系最为特殊,为什么?
归纳:投影线垂直于投影面产生的投影叫做正投影.
意图:从一般到特殊是很多数学问题的研究思路,对于正投影概念的得出,一方面是投影的下位知识,另一方面也体现了“一般——特殊”的研究思路.
活动二 研究线段的正投影
演示:如图,把一根直的细铁丝(记为线段 AB)放在三个不同位置,得到线段 AB的正投影.
观察:三种情形下线段 AB的正投影的形状、大小如何?(可以借助测量等方法)
归纳:通过观察、测量,我们可以发现:
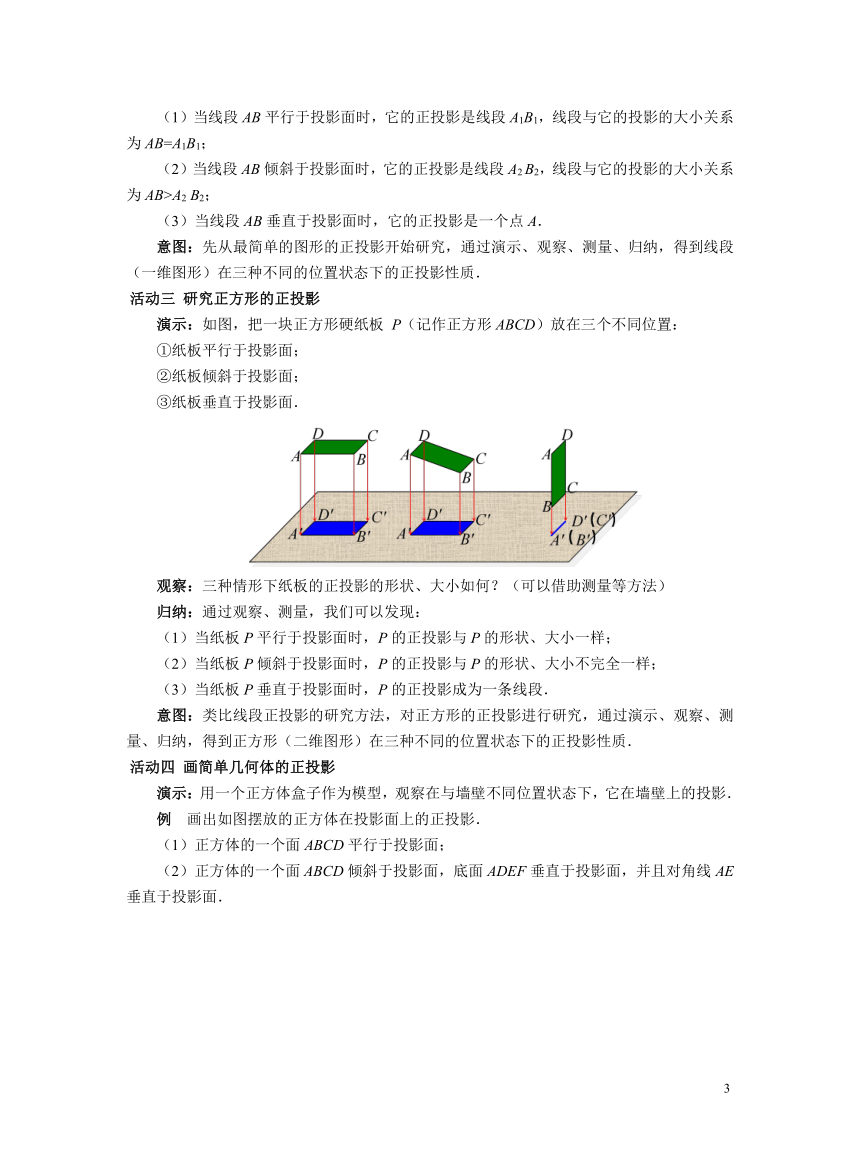
(1)当线段AB平行于投影面时,它的正投影是线段A1B1,线段与它的投影的大小关系为AB=A1B1;
(2)当线段AB倾斜于投影面时,它的正投影是线段A2 B2,线段与它的投影的大小关系为AB>A2 B2;
(3)当线段AB垂直于投影面时,它的正投影是一个点A.
意图:先从最简单的图形的正投影开始研究,通过演示、观察、测量、归纳,得到线段(一维图形)在三种不同的位置状态下的正投影性质.
活动三 研究正方形的正投影
演示:如图,把一块正方形硬纸板 P(记作正方形ABCD)放在三个不同位置:
①纸板平行于投影面;
②纸板倾斜于投影面;
③纸板垂直于投影面.
观察:三种情形下纸板的正投影的形状、大小如何?(可以借助测量等方法)
归纳:通过观察、测量,我们可以发现:
(1)当纸板P平行于投影面时,P的正投影与P的形状、大小一样;
(2)当纸板P倾斜于投影面时,P的正投影与P的形状、大小不完全一样;
(3)当纸板P垂直于投影面时,P的正投影成为一条线段.
意图:类比线段正投影的研究方法,对正方形的正投影进行研究,通过演示、观察、测量、归纳,得到正方形(二维图形)在三种不同的位置状态下的正投影性质.
活动四 画简单几何体的正投影
演示:用一个正方体盒子作为模型,观察在与墙壁不同位置状态下,它在墙壁上的投影.
例 画出如图摆放的正方体在投影面上的正投影.
(1)正方体的一个面ABCD平行于投影面;
(2)正方体的一个面ABCD倾斜于投影面,底面ADEF垂直于投影面,并且对角线AE垂直于投影面.
分析:(1)图中正方体的投影是一个正方形,来自面ABCD,与其垂直的四条棱分别投影为正方形的四个顶点.
(2)图中面ABCD和面ABGF分别投影为矩形A′B′C′D′和A′B′G′F′;正方体其余两个侧面的投影也分别是上述矩形;上下底面的投影分别是线段D′F′和C′G′.正方体的投影F′G′C′D′被线段A′B′一分为二.
解:如图,(1)正方体的正投影为正方形A′B′C′D′,它与正方体的一个面是全等关系.
(2)正方体的正投影为矩形F′G′C′D′,这个矩形的长等于正方体的底面对角线长,矩形的宽等于正方体的棱长.矩形上、下两边中点连线A′B′是正方体的侧棱AB及它所对的另一条侧棱EH的投影.
归纳:正投影的性质
物体正投影的形状、大小与它相对于投影面的位置有关.
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
意图:本例的学习有两方面的作用,一是在学习了一维几何图形(线段)、二维几何图形(正方形)的基础上,研究三维几何图形(正方体)的正投影;二是学习简单几何体的正投影的画法.
(三)课堂练习
1.教材第92页练习题.
2.球的正投影是( B )
A.点 B.圆面 C.圆环 D.椭圆面
3.把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是( A )
4.木棒长为1.2m,则它的正投影的长一定( D )
A.大于1.2m B.小于1.2m
C.等于1.2m D.小于或等于1.2m
5.当棱长为20的正方体的某个面平行于投影面时,这个面的正投影的面积为 400 .
6.画出下列立体图形投影线从上方射向下方的正投影.
解:如图所示:
意图:直接运用本节课所学正投影知识解决简单问题,巩固基础知识,促进基本画图技能的形成.
(四)课堂小结
教师提问:
1.正投影与平行投影有什么关系?
2.画图说明线段、正方形、正方体分别在平行于投影面、倾斜于投影面和垂直于投影面时,正投影的形状和大小.
3.举例说明“一般与特殊”“类比”等数学思想在数学学习的运用.
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:引导学生对本节课所学知识技能进行梳理,对方法过程进行回顾,对思想方法进行反思.
(五)作业布置
A组:教材第92页习题29.1第3-5题.
B组:已知木棒AB长8cm,AB平行于投影面α,投影线垂直于α.
(1)求影子A1B1的长度 (如图①);
(2)若将木棒绕其端点A逆时针旋转30°,求旋转后木棒的影长A2B2 (如图② ).
解:(1) A1B1= AB=8(cm).
(2)如图,A2B2= AE = AB·cos∠BAE =4(cm).
意图:布置分层作业,照顾不同学情的学生,进行自我评估和教学诊断.
六、板书设计
七、课后反思
正投影是研究特殊的平行投影,它的投影线与投影面垂直;正投影的性质重点关注的也是物体与投影面垂直——这种特殊位置关系下的情况.以学习一维几何图形(线段)的正投影为起点,与之类比学习二维几何图形(正方形)的正投影,并在此基础上学习三维几何图形(正方体)的正投影,体现了在知识连贯深化过程中数学思想方法的重要意义.
1
(第2课时)
一、教学内容分析
正投影是建立在平行投影基础上的,是对平行投影知识的延伸.同时,正投影也是后续学习视图知识的基础,由此形成了“投影——平行投影——正投影——视图”的知识链条.由于正投影是在三维空间中进行研究的,所以不可避免的涉及到一些空间图形的位置关系,比如空间中的两条直线平行、直线与平面的平行、斜交与垂直等,对此借助实际物体进行直观描述说明即可.
二、教学目标
1.结合实例,了解正投影的概念,进一步了解投影的意义.
2.根据正投影的性质画出简单几何体的正投影.
3.通过探索几何体及其正投影的关系,体会立体图形与平面图形的相互转化,发展空间观念.
三、教学重难点
【重点】结合具体实例了解正投影的概念和性质.
【难点】画出简单几何体的正投影.
四、教学方法
演示法.由于初中学生接触的主要是平面内一维或二维的几何图形,对于三维空间内的图形认识有限,所以可以借助真实的几何体进行演示,让学生直观感知正投影的形成,并观察其特征.
五、教学过程
(一)新课导入
复习:
1.形成投影有哪些要素?
2.根据投影线(或光源)特征,可以把投影分为哪几种类型?举例说明.
演示:把一块三角板放在一张硬纸板的正上方,使三角板与硬纸板平行,分别在上面用灯泡照射、阳光斜射、阳光直射三种方式,如图所示.
图1 图2 图3
思考:
1.三个演示中的光源、投影线、投影面、投影分别是什么?
2.三个投影中,哪个是中心投影?哪个是平行投影?为什么?
3.平行投影中的投影线与投影面有什么位置关系?
【提示】图1投影线集中于一点,故为中心投影;
图2与图3中投影线互相平行,故为平行投影;
图2中,投影线斜着照射投影面;
图3中投影线垂直照射投影面(即投影线正对着投影面),我们也称这种情形为投影线垂直于投影面.
意图:复习上节课所学的知识,为学习正投影做好铺垫,并顺利导入新课.
(二)新课讲授
活动一 学习正投影的概念
观察:在数学中,经常在一般基础上重点研究特殊情形,观察以上演示中,哪个投影线与投影面的位置关系最为特殊,为什么?
归纳:投影线垂直于投影面产生的投影叫做正投影.
意图:从一般到特殊是很多数学问题的研究思路,对于正投影概念的得出,一方面是投影的下位知识,另一方面也体现了“一般——特殊”的研究思路.
活动二 研究线段的正投影
演示:如图,把一根直的细铁丝(记为线段 AB)放在三个不同位置,得到线段 AB的正投影.
观察:三种情形下线段 AB的正投影的形状、大小如何?(可以借助测量等方法)
归纳:通过观察、测量,我们可以发现:
(1)当线段AB平行于投影面时,它的正投影是线段A1B1,线段与它的投影的大小关系为AB=A1B1;
(2)当线段AB倾斜于投影面时,它的正投影是线段A2 B2,线段与它的投影的大小关系为AB>A2 B2;
(3)当线段AB垂直于投影面时,它的正投影是一个点A.
意图:先从最简单的图形的正投影开始研究,通过演示、观察、测量、归纳,得到线段(一维图形)在三种不同的位置状态下的正投影性质.
活动三 研究正方形的正投影
演示:如图,把一块正方形硬纸板 P(记作正方形ABCD)放在三个不同位置:
①纸板平行于投影面;
②纸板倾斜于投影面;
③纸板垂直于投影面.
观察:三种情形下纸板的正投影的形状、大小如何?(可以借助测量等方法)
归纳:通过观察、测量,我们可以发现:
(1)当纸板P平行于投影面时,P的正投影与P的形状、大小一样;
(2)当纸板P倾斜于投影面时,P的正投影与P的形状、大小不完全一样;
(3)当纸板P垂直于投影面时,P的正投影成为一条线段.
意图:类比线段正投影的研究方法,对正方形的正投影进行研究,通过演示、观察、测量、归纳,得到正方形(二维图形)在三种不同的位置状态下的正投影性质.
活动四 画简单几何体的正投影
演示:用一个正方体盒子作为模型,观察在与墙壁不同位置状态下,它在墙壁上的投影.
例 画出如图摆放的正方体在投影面上的正投影.
(1)正方体的一个面ABCD平行于投影面;
(2)正方体的一个面ABCD倾斜于投影面,底面ADEF垂直于投影面,并且对角线AE垂直于投影面.
分析:(1)图中正方体的投影是一个正方形,来自面ABCD,与其垂直的四条棱分别投影为正方形的四个顶点.
(2)图中面ABCD和面ABGF分别投影为矩形A′B′C′D′和A′B′G′F′;正方体其余两个侧面的投影也分别是上述矩形;上下底面的投影分别是线段D′F′和C′G′.正方体的投影F′G′C′D′被线段A′B′一分为二.
解:如图,(1)正方体的正投影为正方形A′B′C′D′,它与正方体的一个面是全等关系.
(2)正方体的正投影为矩形F′G′C′D′,这个矩形的长等于正方体的底面对角线长,矩形的宽等于正方体的棱长.矩形上、下两边中点连线A′B′是正方体的侧棱AB及它所对的另一条侧棱EH的投影.
归纳:正投影的性质
物体正投影的形状、大小与它相对于投影面的位置有关.
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
意图:本例的学习有两方面的作用,一是在学习了一维几何图形(线段)、二维几何图形(正方形)的基础上,研究三维几何图形(正方体)的正投影;二是学习简单几何体的正投影的画法.
(三)课堂练习
1.教材第92页练习题.
2.球的正投影是( B )
A.点 B.圆面 C.圆环 D.椭圆面
3.把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是( A )
4.木棒长为1.2m,则它的正投影的长一定( D )
A.大于1.2m B.小于1.2m
C.等于1.2m D.小于或等于1.2m
5.当棱长为20的正方体的某个面平行于投影面时,这个面的正投影的面积为 400 .
6.画出下列立体图形投影线从上方射向下方的正投影.
解:如图所示:
意图:直接运用本节课所学正投影知识解决简单问题,巩固基础知识,促进基本画图技能的形成.
(四)课堂小结
教师提问:
1.正投影与平行投影有什么关系?
2.画图说明线段、正方形、正方体分别在平行于投影面、倾斜于投影面和垂直于投影面时,正投影的形状和大小.
3.举例说明“一般与特殊”“类比”等数学思想在数学学习的运用.
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:引导学生对本节课所学知识技能进行梳理,对方法过程进行回顾,对思想方法进行反思.
(五)作业布置
A组:教材第92页习题29.1第3-5题.
B组:已知木棒AB长8cm,AB平行于投影面α,投影线垂直于α.
(1)求影子A1B1的长度 (如图①);
(2)若将木棒绕其端点A逆时针旋转30°,求旋转后木棒的影长A2B2 (如图② ).
解:(1) A1B1= AB=8(cm).
(2)如图,A2B2= AE = AB·cos∠BAE =4(cm).
意图:布置分层作业,照顾不同学情的学生,进行自我评估和教学诊断.
六、板书设计
七、课后反思
正投影是研究特殊的平行投影,它的投影线与投影面垂直;正投影的性质重点关注的也是物体与投影面垂直——这种特殊位置关系下的情况.以学习一维几何图形(线段)的正投影为起点,与之类比学习二维几何图形(正方形)的正投影,并在此基础上学习三维几何图形(正方体)的正投影,体现了在知识连贯深化过程中数学思想方法的重要意义.
1
