初中数学人教版九下29.1投影(第1课时) 教案
文档属性
| 名称 | 初中数学人教版九下29.1投影(第1课时) 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 14:36:13 | ||
图片预览


文档简介
29.1投影
(第1课时)
一、教学内容分析
“如影随形”“形影不离”都反映了现实世界中物体与投影之间的密切关系,当我们用数学的眼光观察现实世界时,会发现一般的物体形状都是三维的立体图形,而它们的影子则是二维平面图形,由物体产生投影是将立体图形转化为平面图形的过程.基于此,对一些日常生活中的投影,有必要上升到数学的角度进行系统研究,本节课就是这个新的研究领域的起点.
二、教学目标
1.了解投影的有关概念,能根据投影线的方向辨认物体的投影.
2.了解中心投影和平行投影的区别.
三、教学重难点
【重点】结合具体实例说明中心投影和平行投影的成因和区别.
【难点】与投影有关的画图和计算问题.
四、教学方法
演示法.虽然在生活中的投影比较常见,但是很多同学们没有留意观察,所以在课堂上可以借助自然光(比如阳光)和人造光(比如蜡烛或灯泡)对物体进行照射,现场演示投影的形成过程,让学生进行观察比较,加深对投影相关概念的了解.
五、教学过程
(一)新课导入
演示:
1.拉上教室的窗帘,营造一个昏暗的环境.
2.一名同学点亮蜡烛(或灯泡),绕着一把椅子(或其他物体)走动,请同学们观察椅子的影子有什么变化,思考这说明什么问题?
(1)蜡烛到椅子的距离相同,但方向不同;
(2)蜡烛在椅子的方向相同,但距离不同.
3.最后走到教室门口,打开门,熄灭蜡烛,请学生观察阳光照射形成的影子和烛光照射形成的影子有何不同,思考这说明什么问题?
意图:一上课营造出一种与众不同的氛围,激发学习兴趣,利用现实生活中的常见现象引导学生思考关于投影的问题.对于学生的回答,不必苛求精准,重在引导学会观察,在后面的学习中再不断完善.
(二)新课讲授
活动一 学习投影的概念
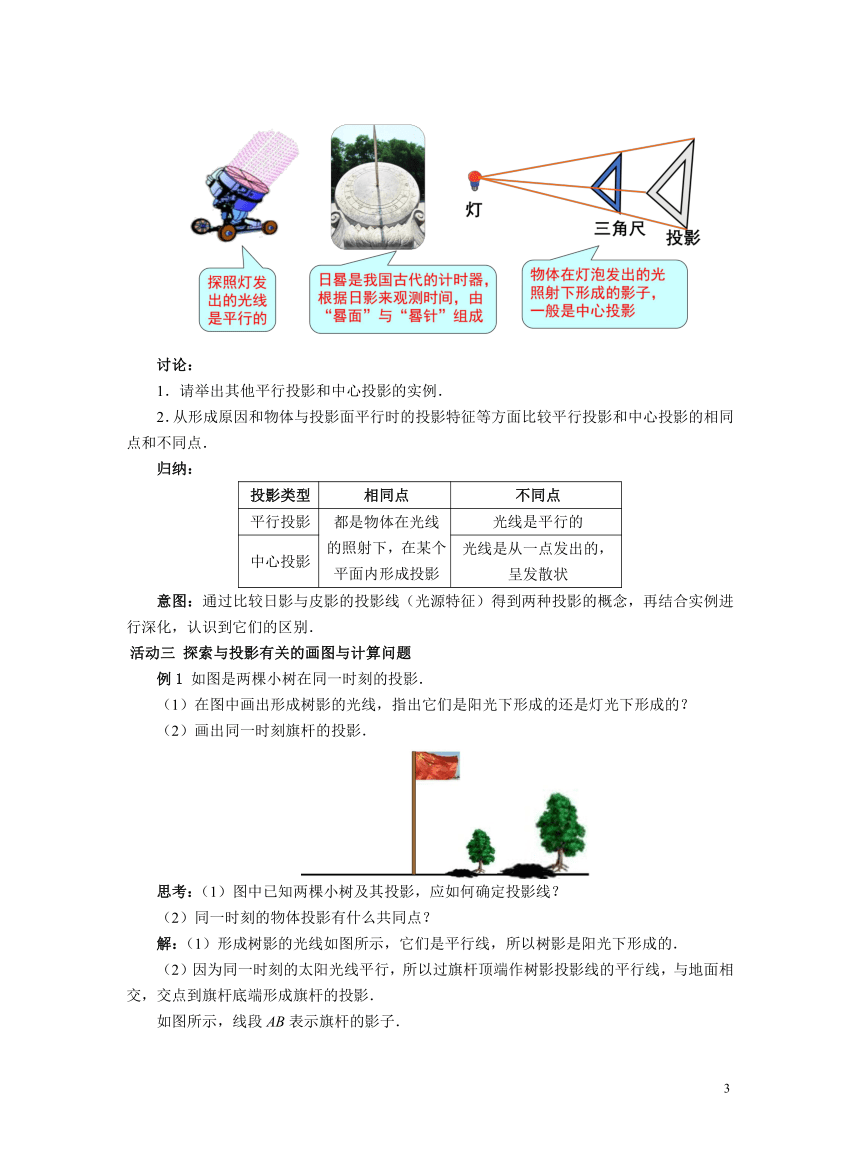
观察:观察以下图片中的物体和影子,并联系现实生活中的其他物体的影子.
思考:物体在日光或灯光的照射下会形成影子,形成影子的因素除这个物体本身外,还需要哪些因素?
归纳:一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影(projection).
照射光线叫做投影线,投影所在的平面叫做投影面.
讨论:皮影戏是利用灯光的照射,把影子的形态反映在银幕上的表演艺术,其中的光源、投影、投影线、投影面分别是什么?
意图:从日常生活中常见的场景入手,引导学生分析形成投影的各个要素,从而得到投影及其相关概念,并在实际问题中加以识别.
活动二 学习平行投影和中心投影
思考:比较太阳光下形成的影子(简称“日影”)与皮影戏中在银幕上的影子(简称“皮影”),从数学的角度来看,它们的一组投影线之间的位置关系是怎样的?
归纳:由平行光线形成的投影是平行投影.
由同一点(点光源)发出的光线形成的投影叫做中心投影.
观察:图中形成的投影哪些是平行投影,哪些是中心投影?分别指出图中出现的光源、投影、投影线、投影面.
讨论:
1.请举出其他平行投影和中心投影的实例.
2.从形成原因和物体与投影面平行时的投影特征等方面比较平行投影和中心投影的相同点和不同点.
归纳:
投影类型 相同点 不同点
平行投影 都是物体在光线的照射下,在某个平面内形成投影 光线是平行的
中心投影 光线是从一点发出的,呈发散状
意图:通过比较日影与皮影的投影线(光源特征)得到两种投影的概念,再结合实例进行深化,认识到它们的区别.
活动三 探索与投影有关的画图与计算问题
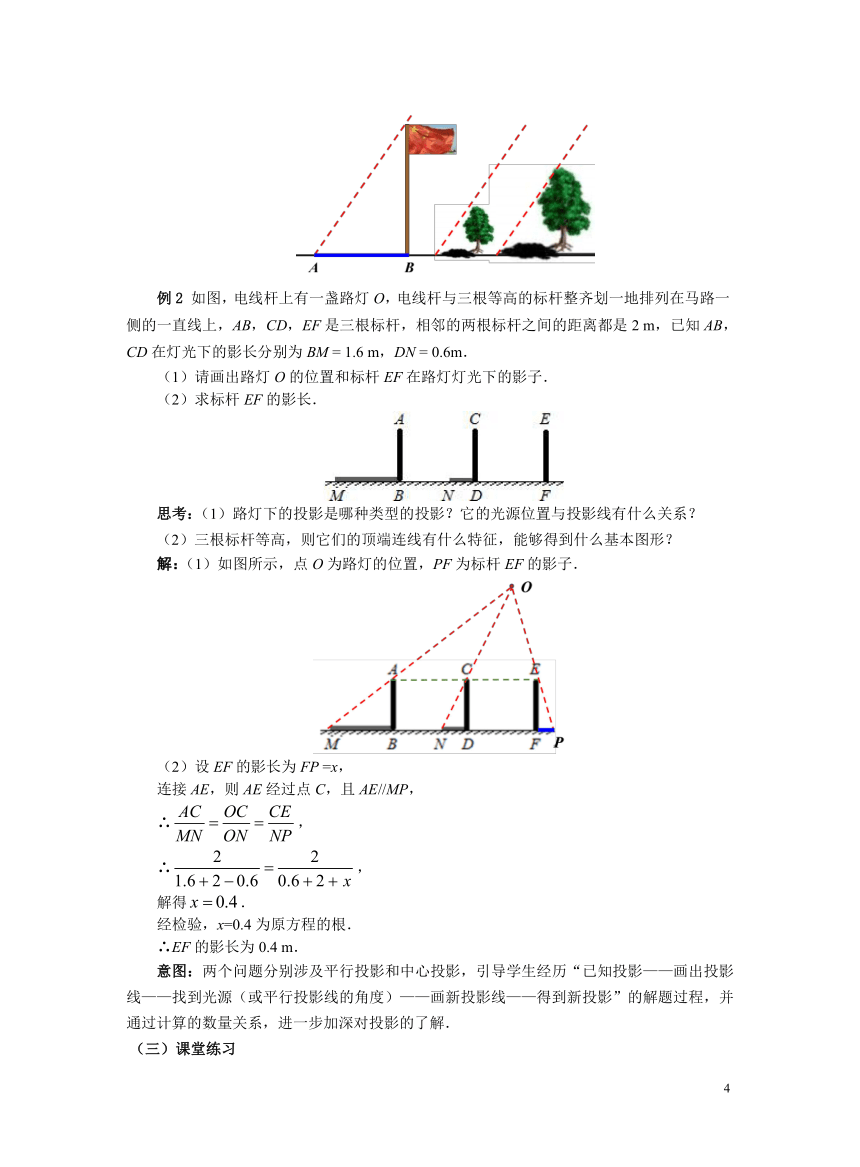
例1 如图是两棵小树在同一时刻的投影.
(1)在图中画出形成树影的光线,指出它们是阳光下形成的还是灯光下形成的?
(2)画出同一时刻旗杆的投影.
思考:(1)图中已知两棵小树及其投影,应如何确定投影线?
(2)同一时刻的物体投影有什么共同点?
解:(1)形成树影的光线如图所示,它们是平行线,所以树影是阳光下形成的.
(2)因为同一时刻的太阳光线平行,所以过旗杆顶端作树影投影线的平行线,与地面相交,交点到旗杆底端形成旗杆的投影.
如图所示,线段AB表示旗杆的影子.
例2 如图,电线杆上有一盏路灯O,电线杆与三根等高的标杆整齐划一地排列在马路一侧的一直线上,AB,CD,EF是三根标杆,相邻的两根标杆之间的距离都是2 m,已知AB,CD在灯光下的影长分别为BM = 1.6 m,DN = 0.6m.
(1)请画出路灯O的位置和标杆EF在路灯灯光下的影子.
(2)求标杆EF的影长.
思考:(1)路灯下的投影是哪种类型的投影?它的光源位置与投影线有什么关系?
(2)三根标杆等高,则它们的顶端连线有什么特征,能够得到什么基本图形?
解:(1)如图所示,点O为路灯的位置,PF为标杆EF的影子.
(2)设EF的影长为FP =x,
连接AE,则AE经过点C,且AE//MP,
∴,
∴,
解得.
经检验,x=0.4为原方程的根.
∴EF的影长为0.4 m.
意图:两个问题分别涉及平行投影和中心投影,引导学生经历“已知投影——画出投影线——找到光源(或平行投影线的角度)——画新投影线——得到新投影”的解题过程,并通过计算的数量关系,进一步加深对投影的了解.
(三)课堂练习
1.教材第88页练习题.
2.下列投影是平行投影的是( A )
A.太阳光下窗户的影子 B.蜡烛照射下的手影
C.路灯下行人的影子 D.台灯下笔的影子
3.下面属于中心投影的是( B )
A.太阳光下的树影 B.吊灯下方的人影
C.月光下房屋的影子 D.海上日出
4.下列物体的影子中,不正确的是 ( B )
5.确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
解:如图所示.
6.学校墙边有甲、乙两根木杆.已知乙杆的高度为1.5m.
(1) 某一时刻甲木杆在阳光下的影子如图所示,请画出此时乙木杆的投影;
(2) 当乙木杆移动到什么位置时,其投影刚好不落在墙上?
(3) 在(2)的情况下,测得甲、乙木杆的影长分别为1.24m和1m,求甲木杆的高度.
解:(1)如图所示,线段BE′表示乙木杆的投影.
(2)如图所示,线段BE表示乙木杆移动到的位置.
(3)解:∵△ADD'∽△BEE',
∴ AD:BE =AD′:BE′,
即AD:1.5 =1.24:1,解得AD =1.86.
故甲木杆的高度为1.86m.
意图:以上练习题穿插在学习新知识的过程中,及时进行跟踪训练,巩固所学知识.
(四)课堂小结
教师提问:
1.形成投影有哪些“要素”?
2.平行投影、中心投影的区别是什么?
3.通过本节课的学习,你对“用数学的眼光观察现实世界”有什么新的认识?
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:前面两个问题在于梳理总结本节课所学的知识要点,形成概念体系;最后一个问题鼓励学生根据自己的真实感受大胆发言,不追求共同答案.
(五)作业布置
A组:教材第92页习题29.1第1,2题.
B组:
1.晚上,人在马路上走过一盏路灯的过程中,其影子长度的变化情况是( A )
A.先变短后变长 B.先变长后变短
C.逐渐变短 D.逐渐变长
2.小亮在上午8:30,9:30,10:00,12:00四次到室外的阳光下,观察广场的旗杆随太阳转动的情况,他发现这四个时刻广场的旗杆在地面上的影子的长度各不相同,那么影子最长的时刻为 8:30 .
3.如图,身高1.6m的小明从距路灯的底部(点O)20m的点A沿AO方向行走14m到点C处,小明在A处,头顶B在路灯投影下形成的影子在M处.
(1)已知灯杆垂直于路面,试标出路灯P的位置和小明在C处头顶D在路灯下的投影N的位置.
(2)若路灯(点P)距地面8m,小明从A到C时,身影的长度是变长了还是变短了?变长或变短了多少m?
解:(1)如图所示:
(2)设在A处时影长AM为xm,在C处时影长CN为ym,
由,解得x=5;
由,解得y=1.5.
∴x﹣y=5﹣1.5=3.5,
∴变短了,变短了3.5m.
意图:A组题目为最基础的简单问题,B组题目有一定综合性,供学有余力的同学选用.
六、板书设计
平行投影与中心投影的联系和区别
七、课后反思
本节课学习了投影的相关概念、分类和简单应用,进一步让学生认识到现实世界中,数学的研究领域可谓无处不在.学习过程中,激发学生的生活经验,引导转化为数学知识.鉴于单纯的投影概念性内容较少,教学目标要求较低,故增加了画图与计算问题,丰富课堂内容,体现知识之间的联系.
1
(第1课时)
一、教学内容分析
“如影随形”“形影不离”都反映了现实世界中物体与投影之间的密切关系,当我们用数学的眼光观察现实世界时,会发现一般的物体形状都是三维的立体图形,而它们的影子则是二维平面图形,由物体产生投影是将立体图形转化为平面图形的过程.基于此,对一些日常生活中的投影,有必要上升到数学的角度进行系统研究,本节课就是这个新的研究领域的起点.
二、教学目标
1.了解投影的有关概念,能根据投影线的方向辨认物体的投影.
2.了解中心投影和平行投影的区别.
三、教学重难点
【重点】结合具体实例说明中心投影和平行投影的成因和区别.
【难点】与投影有关的画图和计算问题.
四、教学方法
演示法.虽然在生活中的投影比较常见,但是很多同学们没有留意观察,所以在课堂上可以借助自然光(比如阳光)和人造光(比如蜡烛或灯泡)对物体进行照射,现场演示投影的形成过程,让学生进行观察比较,加深对投影相关概念的了解.
五、教学过程
(一)新课导入
演示:
1.拉上教室的窗帘,营造一个昏暗的环境.
2.一名同学点亮蜡烛(或灯泡),绕着一把椅子(或其他物体)走动,请同学们观察椅子的影子有什么变化,思考这说明什么问题?
(1)蜡烛到椅子的距离相同,但方向不同;
(2)蜡烛在椅子的方向相同,但距离不同.
3.最后走到教室门口,打开门,熄灭蜡烛,请学生观察阳光照射形成的影子和烛光照射形成的影子有何不同,思考这说明什么问题?
意图:一上课营造出一种与众不同的氛围,激发学习兴趣,利用现实生活中的常见现象引导学生思考关于投影的问题.对于学生的回答,不必苛求精准,重在引导学会观察,在后面的学习中再不断完善.
(二)新课讲授
活动一 学习投影的概念
观察:观察以下图片中的物体和影子,并联系现实生活中的其他物体的影子.
思考:物体在日光或灯光的照射下会形成影子,形成影子的因素除这个物体本身外,还需要哪些因素?
归纳:一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影(projection).
照射光线叫做投影线,投影所在的平面叫做投影面.
讨论:皮影戏是利用灯光的照射,把影子的形态反映在银幕上的表演艺术,其中的光源、投影、投影线、投影面分别是什么?
意图:从日常生活中常见的场景入手,引导学生分析形成投影的各个要素,从而得到投影及其相关概念,并在实际问题中加以识别.
活动二 学习平行投影和中心投影
思考:比较太阳光下形成的影子(简称“日影”)与皮影戏中在银幕上的影子(简称“皮影”),从数学的角度来看,它们的一组投影线之间的位置关系是怎样的?
归纳:由平行光线形成的投影是平行投影.
由同一点(点光源)发出的光线形成的投影叫做中心投影.
观察:图中形成的投影哪些是平行投影,哪些是中心投影?分别指出图中出现的光源、投影、投影线、投影面.
讨论:
1.请举出其他平行投影和中心投影的实例.
2.从形成原因和物体与投影面平行时的投影特征等方面比较平行投影和中心投影的相同点和不同点.
归纳:
投影类型 相同点 不同点
平行投影 都是物体在光线的照射下,在某个平面内形成投影 光线是平行的
中心投影 光线是从一点发出的,呈发散状
意图:通过比较日影与皮影的投影线(光源特征)得到两种投影的概念,再结合实例进行深化,认识到它们的区别.
活动三 探索与投影有关的画图与计算问题
例1 如图是两棵小树在同一时刻的投影.
(1)在图中画出形成树影的光线,指出它们是阳光下形成的还是灯光下形成的?
(2)画出同一时刻旗杆的投影.
思考:(1)图中已知两棵小树及其投影,应如何确定投影线?
(2)同一时刻的物体投影有什么共同点?
解:(1)形成树影的光线如图所示,它们是平行线,所以树影是阳光下形成的.
(2)因为同一时刻的太阳光线平行,所以过旗杆顶端作树影投影线的平行线,与地面相交,交点到旗杆底端形成旗杆的投影.
如图所示,线段AB表示旗杆的影子.
例2 如图,电线杆上有一盏路灯O,电线杆与三根等高的标杆整齐划一地排列在马路一侧的一直线上,AB,CD,EF是三根标杆,相邻的两根标杆之间的距离都是2 m,已知AB,CD在灯光下的影长分别为BM = 1.6 m,DN = 0.6m.
(1)请画出路灯O的位置和标杆EF在路灯灯光下的影子.
(2)求标杆EF的影长.
思考:(1)路灯下的投影是哪种类型的投影?它的光源位置与投影线有什么关系?
(2)三根标杆等高,则它们的顶端连线有什么特征,能够得到什么基本图形?
解:(1)如图所示,点O为路灯的位置,PF为标杆EF的影子.
(2)设EF的影长为FP =x,
连接AE,则AE经过点C,且AE//MP,
∴,
∴,
解得.
经检验,x=0.4为原方程的根.
∴EF的影长为0.4 m.
意图:两个问题分别涉及平行投影和中心投影,引导学生经历“已知投影——画出投影线——找到光源(或平行投影线的角度)——画新投影线——得到新投影”的解题过程,并通过计算的数量关系,进一步加深对投影的了解.
(三)课堂练习
1.教材第88页练习题.
2.下列投影是平行投影的是( A )
A.太阳光下窗户的影子 B.蜡烛照射下的手影
C.路灯下行人的影子 D.台灯下笔的影子
3.下面属于中心投影的是( B )
A.太阳光下的树影 B.吊灯下方的人影
C.月光下房屋的影子 D.海上日出
4.下列物体的影子中,不正确的是 ( B )
5.确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
解:如图所示.
6.学校墙边有甲、乙两根木杆.已知乙杆的高度为1.5m.
(1) 某一时刻甲木杆在阳光下的影子如图所示,请画出此时乙木杆的投影;
(2) 当乙木杆移动到什么位置时,其投影刚好不落在墙上?
(3) 在(2)的情况下,测得甲、乙木杆的影长分别为1.24m和1m,求甲木杆的高度.
解:(1)如图所示,线段BE′表示乙木杆的投影.
(2)如图所示,线段BE表示乙木杆移动到的位置.
(3)解:∵△ADD'∽△BEE',
∴ AD:BE =AD′:BE′,
即AD:1.5 =1.24:1,解得AD =1.86.
故甲木杆的高度为1.86m.
意图:以上练习题穿插在学习新知识的过程中,及时进行跟踪训练,巩固所学知识.
(四)课堂小结
教师提问:
1.形成投影有哪些“要素”?
2.平行投影、中心投影的区别是什么?
3.通过本节课的学习,你对“用数学的眼光观察现实世界”有什么新的认识?
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:前面两个问题在于梳理总结本节课所学的知识要点,形成概念体系;最后一个问题鼓励学生根据自己的真实感受大胆发言,不追求共同答案.
(五)作业布置
A组:教材第92页习题29.1第1,2题.
B组:
1.晚上,人在马路上走过一盏路灯的过程中,其影子长度的变化情况是( A )
A.先变短后变长 B.先变长后变短
C.逐渐变短 D.逐渐变长
2.小亮在上午8:30,9:30,10:00,12:00四次到室外的阳光下,观察广场的旗杆随太阳转动的情况,他发现这四个时刻广场的旗杆在地面上的影子的长度各不相同,那么影子最长的时刻为 8:30 .
3.如图,身高1.6m的小明从距路灯的底部(点O)20m的点A沿AO方向行走14m到点C处,小明在A处,头顶B在路灯投影下形成的影子在M处.
(1)已知灯杆垂直于路面,试标出路灯P的位置和小明在C处头顶D在路灯下的投影N的位置.
(2)若路灯(点P)距地面8m,小明从A到C时,身影的长度是变长了还是变短了?变长或变短了多少m?
解:(1)如图所示:
(2)设在A处时影长AM为xm,在C处时影长CN为ym,
由,解得x=5;
由,解得y=1.5.
∴x﹣y=5﹣1.5=3.5,
∴变短了,变短了3.5m.
意图:A组题目为最基础的简单问题,B组题目有一定综合性,供学有余力的同学选用.
六、板书设计
平行投影与中心投影的联系和区别
七、课后反思
本节课学习了投影的相关概念、分类和简单应用,进一步让学生认识到现实世界中,数学的研究领域可谓无处不在.学习过程中,激发学生的生活经验,引导转化为数学知识.鉴于单纯的投影概念性内容较少,教学目标要求较低,故增加了画图与计算问题,丰富课堂内容,体现知识之间的联系.
1
