初中数学人教版九下28.2.2 应用举例(第1课时) 教案
文档属性
| 名称 | 初中数学人教版九下28.2.2 应用举例(第1课时) 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 830.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 14:13:33 | ||
图片预览


文档简介
28.2.2 应用举例
(第1课时)
一、教学内容分析
学习锐角三角函数的基本过程体现了三个基本数学思想,由实际问题抽象得到三角函数概念,再通过直角三角形相关知识的推理丰富内容,最后用于指导实际问题的建模与解决.本课时主要体现了第三个环节,即用解直角三角形的知识解决现实世界中与视角(包括仰角、俯角)有关的问题.
二、教学目标
1.使学生把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决,进一步提高数学建模能力;
2.利用解直角三角形的相关知识解决太空视角、高度测量等问题,体会数形结合思想的应用价值.
三、教学重难点
【重点】利用解直角三角形的知识解决与视角有关的实际问题.
【难点】根据问题情境画出示意图,归结为解直角三角形问题.
四、教学方法
讨论法.由于本节课所需的知识,比如仰角、俯角、解直角三角形等,在前面都已经学过,所以关键在于把实际问题转化为数学问题,在此过程中充分发挥学生的主体地位,引导学生积极探索发言讨论,在自主探索和小组合作中达成学习目标.
五、教学过程
(一)新课导入
回顾:
1.根据已知条件,解直角三角形问题可以大致分为哪几种类型?
2.解直角三角形的依据有哪些?
【提示】
1.解直角三角形的两种基本类型:
①已知一角(锐角)一边(邻边、对边或斜边),解直角三角形;
②已知两边(两条直角边,或一条直角边斜边 ),解直角三角形.
2.如图,在Rt△ABC中,
(1)三边之间的关系: (勾股定理);
(2)两锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
意图:回顾本节课中解决实际问题所需的主要知识,为新课学习做好铺垫.
(二)新课讲授
活动一 探索太空观察地球问题
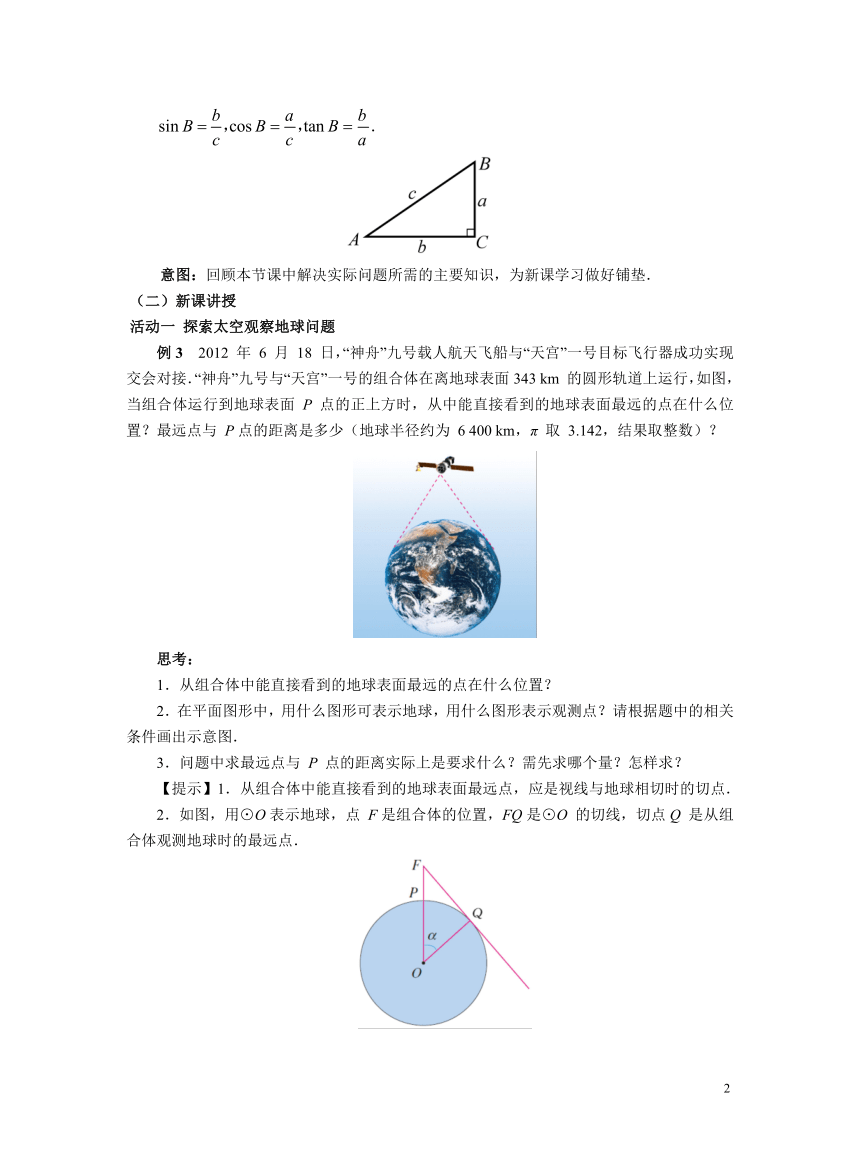
例3 2012 年 6 月 18 日,“神舟”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接.“神舟”九号与“天宫”一号的组合体在离地球表面343 km 的圆形轨道上运行,如图,当组合体运行到地球表面 P 点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与 P点的距离是多少(地球半径约为 6 400 km,π 取 3.142,结果取整数)?
思考:
1.从组合体中能直接看到的地球表面最远的点在什么位置?
2.在平面图形中,用什么图形可表示地球,用什么图形表示观测点?请根据题中的相关条件画出示意图.
3.问题中求最远点与 P 点的距离实际上是要求什么?需先求哪个量?怎样求?
【提示】1.从组合体中能直接看到的地球表面最远点,应是视线与地球相切时的切点.
2.如图,用⊙O表示地球,点 F是组合体的位置,FQ是⊙O 的切线,切点Q 是从组合体观测地球时的最远点.
3.的长就是地面上 P、Q 两点间的距离,为计算的长需先求出∠POQ(即α),α可在Rt△POQ中求解.
解:在图中,FQ 是⊙O的切线,△FOQ 是直角三角形.
∵ cosα== ≈ 0.949 1,
∴ α ≈18.36°.
∴ 的长为×6 400 ≈×6 400≈2 051(km).
由此可知,当组合体在 P点正上方时,从中观测地球表面时的最远点距离P 点约2 051 km.
意图:在对问题的分析过程中,提出一系列思考题,引导学生探索解决太空观察地球两点间距离问题,把实际问题抽象为数学问题.解答思考题,鼓励学生在独立思考的基础上,进行讨论交流,深化认识.
活动二 探索测量建筑物高度问题
例4 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?
观察:结合图形,指出从热气球看楼的视平线、仰角、俯角分别指什么?
思考:从解直角三角形的角度来看,这个问题可抽象为什么问题?怎样解决?
【提示】在直角三角形中,已知一锐角和与这个锐角相邻的直角边,可以利用解直角三角形的知识求这个锐角所对的直角边,再利用两线段之和求解.
解:如图,α=30°,β=60°,AD=120.
∵ tanα=,tanβ=,
∴ BD=AD·tan α=120×tan 30°=120×=40,
CD=AD·tan β=120×tan 60°=120×=120.
∴ BC=BD+CD=40+120=160≈277(m).
答:这栋楼高约为 277 m.
变式 热气球的探测器显示,从热气球看一栋楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?
思考:这道题与例题相比有何变化?应如何解答?
【提示】已知两角都是俯角,在视平线的同侧,
解答时由视平线与楼房CB延长线相交构造直角三角形.
这栋楼高BC=CD-BD=120-40=80≈139(m).
归纳:解决与仰角、俯角有关的测量高度问题:
(1)仰角和俯角是指视线相对于水平线而言的,不同位置的仰角和俯角是不同的,可巧记为“上仰下俯”;
(2)视线、水平线、物体的高构成直角三角形,已知仰角(俯角)和另一边,利用解直角三角形的知识就可以求出物体的高度;
(3)弄清仰角、俯角的定义,根据题意画出几何图形,将实际问题中的数量关系归结到直角三角形中来求解.
意图:通过例题,学习结合仰角和俯角来测量建筑物高度的方法,在具体解题过程中,通过做视平线构造直角三角形,从而为借助解直角三角形知识解答创造条件.
(三)课堂练习
1.“欲穷千里目,更上一层楼”是唐代诗人王之涣的不朽诗句.如果我们想在地球上看到距观测点1000里处景色,“更上一层楼”中的楼至少有多高呢?存在这样的楼房吗?
(设代表地面,O为地球球心,C是地面上一点,=500km,地球的半径为6370 km,cos4.5°= 0.997)
解:设登高到B处,视线BC在点C与地球相切,也就是看到点C,AB就是“楼”的高度,
在Rt△OCB中,∠O
∴ AB=OB-OA=6389-6370=19(km).
即这层楼至少要高19km,即19000m,这是不存在的.
2.教材第76页练习第1题(安排在“活动二”以后练习)
3.教材第76页练习第2题.
意图:课堂练习题与教材例题类型一致,把所学的解题方法进行及时运用,巩固强化,规范解题步骤.
(四)课堂小结
教师提问:
1.本节课学习了哪两种类型的实际问题?
2.解决以上实际问题时,我们要根据题意画出几何图形,如果图中有直角三角形,一般如何解答?如果没有直角三角形,一般如何解答?
3.在解题过程中,用到了哪些数学知识?
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:鼓励学生大胆发言,在独立思考的基础上,与同伴交流,培养学生总结梳理和分享质疑的能力.
(五)作业布置
A组:教材第77页习题28.2第2.3.7.8题.
B组:
1.如图,直升飞机在高为200m的大楼AB上方P点处, 从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO.
解:如图,过点P作PC⊥BA的延长线于点C.
则∠PBO=∠CPB=45°,∠CPA=30°,
∴PC=BC=200+AC,
tan30°=
∴AC=m,
PO=BC=m.
2.如图是一个匀速旋转的摩天轮示意图,O为圆心,AB为水平地面,假设摩天轮的直径为80m,最低点C离地面6m,旋转一周所用的时间为6min,小明从点C乘坐摩天轮(身高忽略不计),请问:经过2min后,小明离地面的高度是多少米?
解:过E作EG垂直于CO的延长线于点G,
∠COE= 2×=120°,∴∠GOE=60°.
∴OG=OE·cos∠GOE=20(m),
∴小明离地面的高度是:OG+OC+CD=20+40+6=66(m).
意图:分层作业,照顾不同学情的学生,其中A组题目注重基础问题的解决,B组题目有一定综合性,供学有余力的同学选用.
六、板书设计
七、课后反思
锐角三角函数“天生”带有强烈的实践特色,所以解直角三角形的应用具有广泛的领域,本课时所列举的是比较常见的两种类型,尤其是利用仰角俯角测量物体的高度,更加符合学生的现实生活;而太空观察地球的问题,虽然显得“高大上”,却体现了数学在高科技方面的应用前景,提高学生的民族自豪感和学习数学的兴趣.
1
(第1课时)
一、教学内容分析
学习锐角三角函数的基本过程体现了三个基本数学思想,由实际问题抽象得到三角函数概念,再通过直角三角形相关知识的推理丰富内容,最后用于指导实际问题的建模与解决.本课时主要体现了第三个环节,即用解直角三角形的知识解决现实世界中与视角(包括仰角、俯角)有关的问题.
二、教学目标
1.使学生把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决,进一步提高数学建模能力;
2.利用解直角三角形的相关知识解决太空视角、高度测量等问题,体会数形结合思想的应用价值.
三、教学重难点
【重点】利用解直角三角形的知识解决与视角有关的实际问题.
【难点】根据问题情境画出示意图,归结为解直角三角形问题.
四、教学方法
讨论法.由于本节课所需的知识,比如仰角、俯角、解直角三角形等,在前面都已经学过,所以关键在于把实际问题转化为数学问题,在此过程中充分发挥学生的主体地位,引导学生积极探索发言讨论,在自主探索和小组合作中达成学习目标.
五、教学过程
(一)新课导入
回顾:
1.根据已知条件,解直角三角形问题可以大致分为哪几种类型?
2.解直角三角形的依据有哪些?
【提示】
1.解直角三角形的两种基本类型:
①已知一角(锐角)一边(邻边、对边或斜边),解直角三角形;
②已知两边(两条直角边,或一条直角边斜边 ),解直角三角形.
2.如图,在Rt△ABC中,
(1)三边之间的关系: (勾股定理);
(2)两锐角之间的关系:∠A+∠B=90°;
(3)边角之间的关系:
意图:回顾本节课中解决实际问题所需的主要知识,为新课学习做好铺垫.
(二)新课讲授
活动一 探索太空观察地球问题
例3 2012 年 6 月 18 日,“神舟”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接.“神舟”九号与“天宫”一号的组合体在离地球表面343 km 的圆形轨道上运行,如图,当组合体运行到地球表面 P 点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与 P点的距离是多少(地球半径约为 6 400 km,π 取 3.142,结果取整数)?
思考:
1.从组合体中能直接看到的地球表面最远的点在什么位置?
2.在平面图形中,用什么图形可表示地球,用什么图形表示观测点?请根据题中的相关条件画出示意图.
3.问题中求最远点与 P 点的距离实际上是要求什么?需先求哪个量?怎样求?
【提示】1.从组合体中能直接看到的地球表面最远点,应是视线与地球相切时的切点.
2.如图,用⊙O表示地球,点 F是组合体的位置,FQ是⊙O 的切线,切点Q 是从组合体观测地球时的最远点.
3.的长就是地面上 P、Q 两点间的距离,为计算的长需先求出∠POQ(即α),α可在Rt△POQ中求解.
解:在图中,FQ 是⊙O的切线,△FOQ 是直角三角形.
∵ cosα== ≈ 0.949 1,
∴ α ≈18.36°.
∴ 的长为×6 400 ≈×6 400≈2 051(km).
由此可知,当组合体在 P点正上方时,从中观测地球表面时的最远点距离P 点约2 051 km.
意图:在对问题的分析过程中,提出一系列思考题,引导学生探索解决太空观察地球两点间距离问题,把实际问题抽象为数学问题.解答思考题,鼓励学生在独立思考的基础上,进行讨论交流,深化认识.
活动二 探索测量建筑物高度问题
例4 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?
观察:结合图形,指出从热气球看楼的视平线、仰角、俯角分别指什么?
思考:从解直角三角形的角度来看,这个问题可抽象为什么问题?怎样解决?
【提示】在直角三角形中,已知一锐角和与这个锐角相邻的直角边,可以利用解直角三角形的知识求这个锐角所对的直角边,再利用两线段之和求解.
解:如图,α=30°,β=60°,AD=120.
∵ tanα=,tanβ=,
∴ BD=AD·tan α=120×tan 30°=120×=40,
CD=AD·tan β=120×tan 60°=120×=120.
∴ BC=BD+CD=40+120=160≈277(m).
答:这栋楼高约为 277 m.
变式 热气球的探测器显示,从热气球看一栋楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?
思考:这道题与例题相比有何变化?应如何解答?
【提示】已知两角都是俯角,在视平线的同侧,
解答时由视平线与楼房CB延长线相交构造直角三角形.
这栋楼高BC=CD-BD=120-40=80≈139(m).
归纳:解决与仰角、俯角有关的测量高度问题:
(1)仰角和俯角是指视线相对于水平线而言的,不同位置的仰角和俯角是不同的,可巧记为“上仰下俯”;
(2)视线、水平线、物体的高构成直角三角形,已知仰角(俯角)和另一边,利用解直角三角形的知识就可以求出物体的高度;
(3)弄清仰角、俯角的定义,根据题意画出几何图形,将实际问题中的数量关系归结到直角三角形中来求解.
意图:通过例题,学习结合仰角和俯角来测量建筑物高度的方法,在具体解题过程中,通过做视平线构造直角三角形,从而为借助解直角三角形知识解答创造条件.
(三)课堂练习
1.“欲穷千里目,更上一层楼”是唐代诗人王之涣的不朽诗句.如果我们想在地球上看到距观测点1000里处景色,“更上一层楼”中的楼至少有多高呢?存在这样的楼房吗?
(设代表地面,O为地球球心,C是地面上一点,=500km,地球的半径为6370 km,cos4.5°= 0.997)
解:设登高到B处,视线BC在点C与地球相切,也就是看到点C,AB就是“楼”的高度,
在Rt△OCB中,∠O
∴ AB=OB-OA=6389-6370=19(km).
即这层楼至少要高19km,即19000m,这是不存在的.
2.教材第76页练习第1题(安排在“活动二”以后练习)
3.教材第76页练习第2题.
意图:课堂练习题与教材例题类型一致,把所学的解题方法进行及时运用,巩固强化,规范解题步骤.
(四)课堂小结
教师提问:
1.本节课学习了哪两种类型的实际问题?
2.解决以上实际问题时,我们要根据题意画出几何图形,如果图中有直角三角形,一般如何解答?如果没有直角三角形,一般如何解答?
3.在解题过程中,用到了哪些数学知识?
在学生自由发言的基础上,与同伴进行交流,师生共同总结.
意图:鼓励学生大胆发言,在独立思考的基础上,与同伴交流,培养学生总结梳理和分享质疑的能力.
(五)作业布置
A组:教材第77页习题28.2第2.3.7.8题.
B组:
1.如图,直升飞机在高为200m的大楼AB上方P点处, 从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO.
解:如图,过点P作PC⊥BA的延长线于点C.
则∠PBO=∠CPB=45°,∠CPA=30°,
∴PC=BC=200+AC,
tan30°=
∴AC=m,
PO=BC=m.
2.如图是一个匀速旋转的摩天轮示意图,O为圆心,AB为水平地面,假设摩天轮的直径为80m,最低点C离地面6m,旋转一周所用的时间为6min,小明从点C乘坐摩天轮(身高忽略不计),请问:经过2min后,小明离地面的高度是多少米?
解:过E作EG垂直于CO的延长线于点G,
∠COE= 2×=120°,∴∠GOE=60°.
∴OG=OE·cos∠GOE=20(m),
∴小明离地面的高度是:OG+OC+CD=20+40+6=66(m).
意图:分层作业,照顾不同学情的学生,其中A组题目注重基础问题的解决,B组题目有一定综合性,供学有余力的同学选用.
六、板书设计
七、课后反思
锐角三角函数“天生”带有强烈的实践特色,所以解直角三角形的应用具有广泛的领域,本课时所列举的是比较常见的两种类型,尤其是利用仰角俯角测量物体的高度,更加符合学生的现实生活;而太空观察地球的问题,虽然显得“高大上”,却体现了数学在高科技方面的应用前景,提高学生的民族自豪感和学习数学的兴趣.
1
