第一章 专题01绝对值与有理数的运算(30题)(含解析)2023-2024学年七年级数学上册人教版
文档属性
| 名称 | 第一章 专题01绝对值与有理数的运算(30题)(含解析)2023-2024学年七年级数学上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 623.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 13:55:35 | ||
图片预览




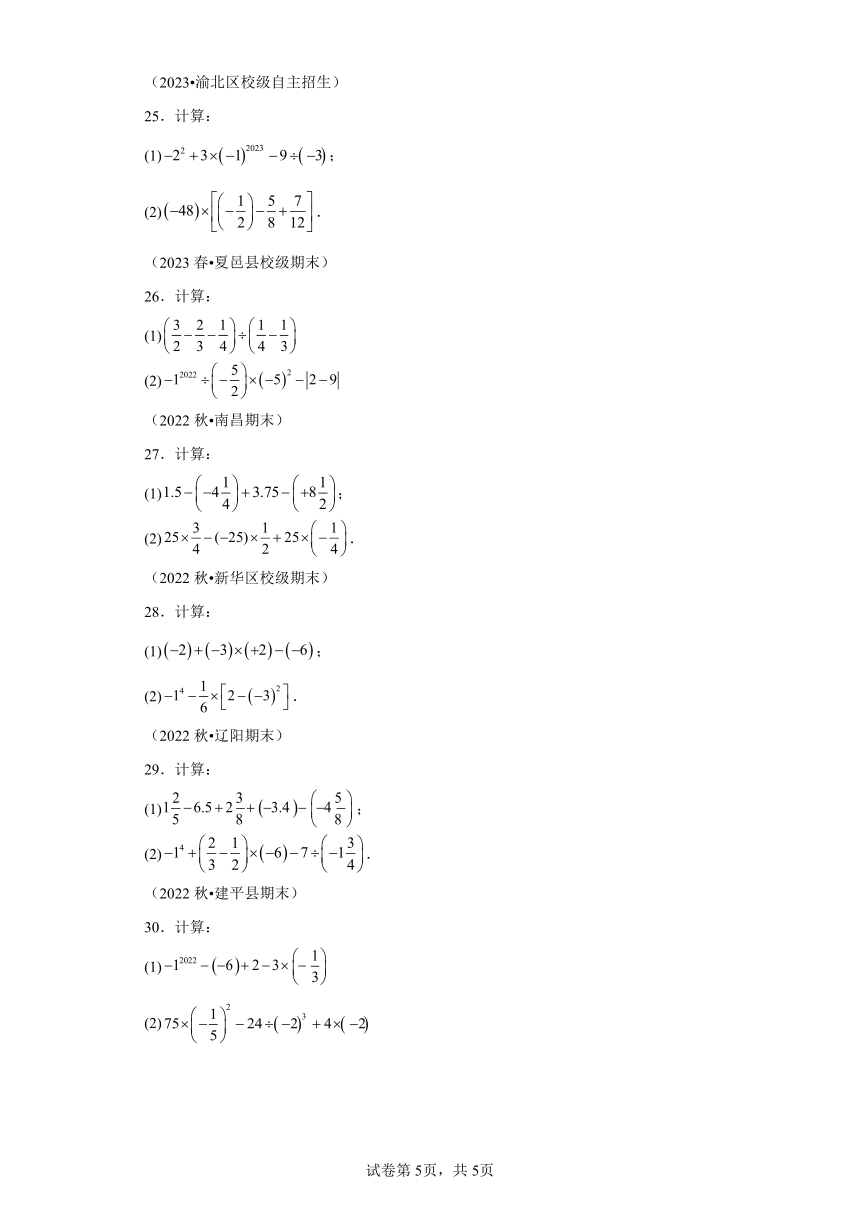
文档简介
专题第01讲 绝对值与有理数的运算(30题)
(2022秋 建邺区校级期末)
1.有理数a、b、c在数轴上的位置如图.
(1)用“”或“”填空: 0, 0, 0.
(2)化简:.
(2023 新华区校级模拟)
2.已知有理数a,b,c在数轴上对应位置如图所示:
(1)用“<”或“>”填空: 0, 0, 0, 0;
(2)化简: .
(2022秋 丰泽区校级期末)
3.若用点A、B、C分别表示有理数a、b、c如图:
(1)判断下列各式的符号:a+b 0;c﹣b 0;c-a 0
(2)化简|a+b|﹣|c﹣b|﹣|c﹣a|
(2022秋 越秀区期末)
4.有理数a、b、c在数轴上的位置如图所示.
(1)比较大小:______0;______0;______0.(直接在横线上填“>”,“=”,“<”中的一个);
(2)化简:.
(2022秋 万州区期末)
5.有理数a,b,c在数轴上对应点的位置如图所示.
(1)在数轴上表示.
(2)试把这五个数从小到大用“”连接起来;
(3)化简
(2022秋 庐江县期末)
6.有理数a、b、c在数轴上的位置如图:
(1)判断正负,用“”或“”填空:___0,___0,___0;
(2)化简:.
(2022秋 长沙期末)
7.有理数a、b、c在数轴上的位置如图,
(1)用“”或“”填空∶_______0,_______0,_______0;
(2)化简∶.
(2022秋 荔湾区校级期末)
8.有理数a、b、c在数轴上的位置如图所示.
(1)用“<”连接:0、a、﹣b、c.
(2)化简:|a+c|+2|c﹣b|﹣|a+b|.
(2022秋 渠县校级期末)
9.a、b、c三个数在数轴上位置如图所示,且|a|=|b|
(1)求出a、b、c各数的绝对值;
(2)比较a,﹣a、﹣c的大小;
(3)化简|a+b|+|a﹣b|+|a+c|+|b﹣c|.
(2022秋 市中区校级期末)
10.有理数a、b、c在数轴上的位置如图.
(1)用“>”或“<”填空: 0, 0, 0, 0.
(2)化简:.
(2022秋 连云港期末)
11.计算:
(1);
(2)
(2023春 无锡月考)
12.计算:
(1);
(2).
(2022秋 南通期末)
13.计算:
(1);
(2).
(2022秋 姜堰区期末)
14.计算:
(1)
(2)
(2022秋 市中区校级期末)
15.计算:
(1)
(2)
(2022秋 宝应县期末)
16.计算:
(1)
(2)
(2022秋 涵江区期末)
17.计算:
(1)
(2)
(2022秋 梁子湖区期末)
18.计算:
(1);
(2).
(2022秋 汉川市期末)
19.计算:
(1);
(2)
(2022秋 梅里斯区期末)
20.计算
(1)
(2)
(2022秋 仓山区期末)
21.计算:
(1);
(2).
(2023 官渡区校级开学)
22.计算:
(1);
(2);
(3).
(2022秋 南阳期末)
23.计算下列各题:
(1);
(2).
(2022秋 沈丘县月考)
24.计算:
(1);
(2).
(2023 渝北区校级自主招生)
25.计算:
(1);
(2).
(2023春 夏邑县校级期末)
26.计算:
(1)
(2)
(2022秋 南昌期末)
27.计算:
(1);
(2).
(2022秋 新华区校级期末)
28.计算:
(1);
(2).
(2022秋 辽阳期末)
29.计算:
(1);
(2).
(2022秋 建平县期末)
30.计算:
(1)
(2)
试卷第4页,共5页
试卷第1页,共5页
参考答案:
1.(1)
(2)
【分析】(1)先根据数轴上点的位置得到,,再根据有理数的加减计算法则即可判断个式子的符号;
(2)根据(1)所求先去绝对值,再根据整式的加减计算法则求解即可.
【详解】(1)解:由题意得,,
∴,
故答案为:;
(2)解:∵,
∴
.
【点睛】本题主要考查了化简绝对值,根据数轴上点的位置判断式子符号,有理数的加减计算,整式的加减计算,正确判断出是解题的关键.
2.(1)<;<;>;>
(2)
【分析】(1)根据数轴可知:,且,由有理数的加减法法则可得答案;
(2)根据数轴比较、、、与0的大小,然后进行化简运算即可.
【详解】(1)解:由图可知:,且,
∴;
故答案为:<;<;>;>;
(2)原式=
=
=
=
=.
【点睛】本题考查根据数轴上点的位置判断式子的正负、整式的加减运算,正确判断式子的正负是解题的关键.
3.(1)<,<,>;(2)﹣2b.
【分析】(1)数轴上的数,右边的数总比左边的数大,利用这个特点可比较三个数的大小.
(2)由数轴可知:b>0,a<c<0,所以可知:a+b<0,c-b<0, c-a>0.根据负数的绝对值是它的相反数可求值.
【详解】解:(1)a+b<0,c﹣b<0,c﹣a>0.
故答案为<,<,>;
(2)|a+b|﹣|c﹣b|﹣|c﹣a|
=﹣(a+b)+(c﹣b)﹣(c﹣a)
=﹣a﹣b+c﹣b﹣c+a
=﹣2b.
【点睛】此题考查绝对值,有理数大小比较,数轴,解题关键在于结合数轴判断各数的大小.
4.(1)<,<,>;
(2);
【分析】(1)根据数轴得到a,b,0,c,之间的关系,结合有理数加减法则即可得到答案;
(2)根据绝对值的性质去绝对值化简即可得到答案;
【详解】(1)解:由数轴可得,
,
∴,,,
故答案为:<,<,>;
(2)解:由(1)可得,
原式
.
【点睛】本题考查数轴上点之间关系,有理数加减运算法则,绝对值的性质,解题的关键是根据数轴得到式子与0的关系.
5.(1)详见解析
(2)
(3)
【分析】(1)直接在数轴上标出,即可求解;
(2)直接观察数轴,即可求解;
(3)根据题意可得,再根据绝对值的性质化简,再合并,即可求解.
【详解】(1)解:在数轴上表示.如图:
(2)解:把这五个数从小到大用“”连接起来如下:
;
(3)解:∵,
∴,
原式
【点睛】本题主要考查了数轴,就绝对值的性质,整式的加减混合运算,利用数形结合思想解答是解题的关键.
6.(1),,
(2)
【分析】(1)根据a、b、c在数轴上的位置,即可判定它们的正负及绝对值的大小,据此即可解答;
(2)根据(1)中的结论,化简绝对值,再进行整式的加减运算,即可求得结果.
【详解】(1)解:由图可知,,,且,
所以,,;
故答案为:,,;
(2)解:,,,
.
【点睛】本题考查了利用数轴判断式子的符号,化简绝对值符号,整式的加减运算,准确判断出各式子的符号是解决本题的关键.
7.(1),,
(2)
【分析】(1)根据各点在数轴上的位置上判断出其符号及绝对值的大小,进而可得出结论;
(2)根据(1)中的结论去绝对值符号,合并同类项即可.
【详解】(1)解:∵由有理数a、b、c在数轴上的位置可知,,,
∴,,.
故答案为:,,;
(2)
【点睛】本题考查的是有理数的大小比较,熟知数轴上右边的数比左边的大是解题的关键.
8.(1)a<0<c<﹣b
(2)c﹣b
【分析】(1)根据各点在数轴上的位置判断出a、b、c的符号及绝对值的大小,再从左到右用“<”连接起来即可
(2)根据(1)中a、b、c的符号判断出各式的符号,再去绝对值符号,合并同类项即可.
【详解】(1)解:画出在数轴上的位置如图:
由图可知,,
;
(2)由(1)可知,,
,,,
原式,
,
.
【点睛】本题考查的是有理数的大小比较,熟知数轴上右边的数总比左边的大是解题的关键.
9.(1)|a|=a,|b|=﹣b,|c|=﹣c;(2)﹣a<a<﹣c;(3)﹣2c.
【分析】(1)根据图示可知c(2)根据数轴上点的位置以及绝对值进行比较即可得;
(3)根据题意得:a+b=0,a﹣b>0,a+c<0,b﹣c>0,由此进行化简即可得结果.
【详解】(1)∵从数轴可知:c<b<0<a,
∴|a|=a,|b|=﹣b,|c|=﹣c;
(2)∵从数轴可知:c<b<0<a,|c|>|a|,
∴﹣a<a<﹣c;
(3)根据题意得:a+b=0,a﹣b>0,a+c<0,b﹣c>0,
则|a+b|+|a﹣b|+|a+c|+|b﹣c|
=0+a-b﹣a﹣c+b-c
=﹣2c.
【点睛】本题考查了数轴、绝对值的化简、有理数大小比较等,读懂数轴、熟练应用相关知识是解题的关键.
10.(1)
(2)
【分析】(1)先判断再结合相反数,有理数的减法运算可得答案;
(2)由再根据化简绝对值的法则化简绝对值,再合并即可.
【详解】(1)解:∵
∴
故答案为:.
(2)结合(1)可得:
【点睛】本题考查的是利用数轴比较有理数的大小,绝对值的含义,化简绝对值,有理数的减法法则的理解,去括号,合并同类项,掌握“绝对值的化简方法”是解本题的关键.
11.(1)
(2)
【分析】(1)先乘除,再进行加法运算;
(2)先乘方,再乘除,最后算减法.
【详解】(1)解:原式
;
(2)原式
.
【点睛】本题考查有理数的混合运算,熟练掌握有理数的运算法则,是解题的关键.
12.(1);
(2).
【分析】(1)用有理数的加法的法则和减法的法则从左到右依次计算;
(2)先用有理数乘方的法则计算乘方,再用有理数的乘法的法则和除法的法则计算乘除,最后用有理数的加法的法则和减法的法则计算加减.
【详解】(1)解:
(2)
【点睛】本题主要考查了有理数的混合运算,解决问题的关键是熟练掌握混合运算的顺序,乘方、乘除、加减的运算法则.
13.(1)5;
(2)0.
【分析】(1)根据有理数的加减法可以解答本题;
(2)先算乘方,再算乘除法,最后算加减,可以解答本题.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
14.(1);
(2).
【分析】(1)根据有理数的加减运算,求解即可;
(2)根据有理数的乘方以及四则混合运算,求解即可.
【详解】(1)解:;
(2)解:
.
【点睛】此题考查了有理数的乘方以及四则混合运算,解题的关键是熟练掌握有理数的有关运算法则.
15.(1)
(2)
【分析】(1)根据有理数的加减混合运算进行计算即可求解;
(2)根据有理数的混合运算进行计算即可求解.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查了有理数的混合运算,掌握有理数的运算法则是解题的关键.
16.(1)
(2)
【分析】(1)根据有理数的加减进行计算即可求解;
(2)根据有理数的混合运算进行计算即可求解.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查了有理数的混合运算,掌握有理数的运算法则是解题的关键.
17.(1)-8
(2)-1
【分析】(1)原式先去括号,再计算即可得到答案.
(2)原式先计算乘方,再计算乘除、去绝对值,最后进行加减运算即可求解.
【详解】(1)原式
.
(2)原式
.
【点睛】此题考查了有理数的混合运算,熟练掌握运算法则是本题的关键.
18.(1)
(2)0
【分析】(1)先计算乘方,同时根据乘法分配律进行计算即可求解;
(2)根据有理数的混合运算顺序进行计算即可求解.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查了有理数的混合运算,掌握有理数的运算顺序以及有理数的运算法则是解题的关键.
19.(1)9
(2)6
【分析】(1)根据有理数的混合运算法则计算即可;
(2)根据有理数的混合运算法则计算即可.
【详解】(1)
;
(2)
.
【点睛】本题考查了有理数的四则混合,掌握有理数的四则混合运算法则是解答本题的关键.
20.(1)
(2)
【分析】(1)根据有理数四则混合运算法则进行计算即可;
(2)根据含乘方的有理数混合运算法则进行计算即可.
【详解】(1)解:
;
(2)解:
.
【点睛】本题主要考查了有理数混合运算,解题的关键是熟练掌握运算法则,准确计算.
21.(1);
(2).
【分析】(1)根据乘法分配律简便计算;
(2)根据有理数的乘方、有理数的乘除法和加减法可以解答本题.
【详解】(1)解:
;
(2)解:
.
【点睛】本题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,注意乘法运算定律的应用.
22.(1)1
(2)8
(3)
【分析】(1)根据有理数的加减法可以解答本题;
(2)先算乘方,再算乘法,最后算加减;如果有括号,要先做括号内的运算;
(3)先把除法运算转化成乘法运算,再根据乘法分配律计算.
【详解】(1)解:
;
(2)解:
;
(3)解:
.
【点睛】本题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,注意乘法运算定律的应用.
23.(1)7
(2)5
【分析】(1)先算乘方,再算乘除法,最后算加减法即可;
(2)先算乘方和括号内的式子,再算乘除法,最后算加减法即可.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查了含有乘方的有理数混合运算,熟练掌握运算法则和运算顺序是解题的关键.
24.(1)49
(2)13
【分析】(1)先算乘方,把除法转为乘法,再算乘法,最后算加法即可;
(2)先算乘法,再算加减即可.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查的是有理数的混合运算,需要熟练掌握有理数的混合运算法则.
25.(1)
(2)
【分析】(1)先计算有理数的乘方,再根据有理数的混合运算法则计算即可;
(2)根据乘法分配律计算即可.
【详解】(1)解:
;
(2)
.
【点睛】本题考查了有理数的混合运算,解题的关键是掌握有理数的混合运算顺序和法则.
26.(1)
(2)3
【分析】(1)先算第2项括号里的,除法转换为乘法,再根据乘法分配律展开,最后计算加减即可;
(2)先算乘方,化简绝对值,根据法则进一步处理.
【详解】(1)解:
;
(2)
.
【点睛】本题考查有理数的混合运算,注意运算中符号的处理,掌握运算法则是解题的关键.
27.(1)1
(2)25
【分析】(1)先把分数化成小数,然后再利用有理数加减运算法则计算即可;
(2)直角运用乘法结合律计算即可.
【详解】(1)解:
=
=
=-7+8
=1.
(2)解:
=
=
=25.
【点睛】本题主要考查了有理数的加减混合运算、乘法结合律等知识点,灵活应用相关运算法则和运算律成为解答本题的关键.
28.(1)
(2)
【分析】(1)先算乘法,再算加减法即可;
(2)先算乘方和括号内的式子,然后算乘法,最后算减法即可.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查的是有理数的混合运算,熟练掌握有理数的混合运算法则是解题的关键.
29.(1)
(2)2
【分析】对于(1),先将小数变为分数,同时去括号,再根据有理数的加减法法则计算即可;
对于(2),先算乘方,同时计算括号内的,再计算乘除法,最后计算加减.
【详解】(1)原式
;
(2)原式
.
【点睛】本题主要考查了有理数的混合运算,掌握运算法则是解题的关键.即先算乘方,再算乘除,最后算加减,有括号的先计算括号内的.
30.(1)8
(2)
【分析】根据先乘方,再算乘除法,最后再算加减的有理数混合运算顺序进行计算即可.
【详解】(1)解:原式
;
(2)解:原式
.
【点睛】本题考查了含乘方的有理数的混合运算,熟练掌握有理数的混合运算顺序是计算本题的关键.
答案第16页,共17页
答案第17页,共17页
(2022秋 建邺区校级期末)
1.有理数a、b、c在数轴上的位置如图.
(1)用“”或“”填空: 0, 0, 0.
(2)化简:.
(2023 新华区校级模拟)
2.已知有理数a,b,c在数轴上对应位置如图所示:
(1)用“<”或“>”填空: 0, 0, 0, 0;
(2)化简: .
(2022秋 丰泽区校级期末)
3.若用点A、B、C分别表示有理数a、b、c如图:
(1)判断下列各式的符号:a+b 0;c﹣b 0;c-a 0
(2)化简|a+b|﹣|c﹣b|﹣|c﹣a|
(2022秋 越秀区期末)
4.有理数a、b、c在数轴上的位置如图所示.
(1)比较大小:______0;______0;______0.(直接在横线上填“>”,“=”,“<”中的一个);
(2)化简:.
(2022秋 万州区期末)
5.有理数a,b,c在数轴上对应点的位置如图所示.
(1)在数轴上表示.
(2)试把这五个数从小到大用“”连接起来;
(3)化简
(2022秋 庐江县期末)
6.有理数a、b、c在数轴上的位置如图:
(1)判断正负,用“”或“”填空:___0,___0,___0;
(2)化简:.
(2022秋 长沙期末)
7.有理数a、b、c在数轴上的位置如图,
(1)用“”或“”填空∶_______0,_______0,_______0;
(2)化简∶.
(2022秋 荔湾区校级期末)
8.有理数a、b、c在数轴上的位置如图所示.
(1)用“<”连接:0、a、﹣b、c.
(2)化简:|a+c|+2|c﹣b|﹣|a+b|.
(2022秋 渠县校级期末)
9.a、b、c三个数在数轴上位置如图所示,且|a|=|b|
(1)求出a、b、c各数的绝对值;
(2)比较a,﹣a、﹣c的大小;
(3)化简|a+b|+|a﹣b|+|a+c|+|b﹣c|.
(2022秋 市中区校级期末)
10.有理数a、b、c在数轴上的位置如图.
(1)用“>”或“<”填空: 0, 0, 0, 0.
(2)化简:.
(2022秋 连云港期末)
11.计算:
(1);
(2)
(2023春 无锡月考)
12.计算:
(1);
(2).
(2022秋 南通期末)
13.计算:
(1);
(2).
(2022秋 姜堰区期末)
14.计算:
(1)
(2)
(2022秋 市中区校级期末)
15.计算:
(1)
(2)
(2022秋 宝应县期末)
16.计算:
(1)
(2)
(2022秋 涵江区期末)
17.计算:
(1)
(2)
(2022秋 梁子湖区期末)
18.计算:
(1);
(2).
(2022秋 汉川市期末)
19.计算:
(1);
(2)
(2022秋 梅里斯区期末)
20.计算
(1)
(2)
(2022秋 仓山区期末)
21.计算:
(1);
(2).
(2023 官渡区校级开学)
22.计算:
(1);
(2);
(3).
(2022秋 南阳期末)
23.计算下列各题:
(1);
(2).
(2022秋 沈丘县月考)
24.计算:
(1);
(2).
(2023 渝北区校级自主招生)
25.计算:
(1);
(2).
(2023春 夏邑县校级期末)
26.计算:
(1)
(2)
(2022秋 南昌期末)
27.计算:
(1);
(2).
(2022秋 新华区校级期末)
28.计算:
(1);
(2).
(2022秋 辽阳期末)
29.计算:
(1);
(2).
(2022秋 建平县期末)
30.计算:
(1)
(2)
试卷第4页,共5页
试卷第1页,共5页
参考答案:
1.(1)
(2)
【分析】(1)先根据数轴上点的位置得到,,再根据有理数的加减计算法则即可判断个式子的符号;
(2)根据(1)所求先去绝对值,再根据整式的加减计算法则求解即可.
【详解】(1)解:由题意得,,
∴,
故答案为:;
(2)解:∵,
∴
.
【点睛】本题主要考查了化简绝对值,根据数轴上点的位置判断式子符号,有理数的加减计算,整式的加减计算,正确判断出是解题的关键.
2.(1)<;<;>;>
(2)
【分析】(1)根据数轴可知:,且,由有理数的加减法法则可得答案;
(2)根据数轴比较、、、与0的大小,然后进行化简运算即可.
【详解】(1)解:由图可知:,且,
∴;
故答案为:<;<;>;>;
(2)原式=
=
=
=
=.
【点睛】本题考查根据数轴上点的位置判断式子的正负、整式的加减运算,正确判断式子的正负是解题的关键.
3.(1)<,<,>;(2)﹣2b.
【分析】(1)数轴上的数,右边的数总比左边的数大,利用这个特点可比较三个数的大小.
(2)由数轴可知:b>0,a<c<0,所以可知:a+b<0,c-b<0, c-a>0.根据负数的绝对值是它的相反数可求值.
【详解】解:(1)a+b<0,c﹣b<0,c﹣a>0.
故答案为<,<,>;
(2)|a+b|﹣|c﹣b|﹣|c﹣a|
=﹣(a+b)+(c﹣b)﹣(c﹣a)
=﹣a﹣b+c﹣b﹣c+a
=﹣2b.
【点睛】此题考查绝对值,有理数大小比较,数轴,解题关键在于结合数轴判断各数的大小.
4.(1)<,<,>;
(2);
【分析】(1)根据数轴得到a,b,0,c,之间的关系,结合有理数加减法则即可得到答案;
(2)根据绝对值的性质去绝对值化简即可得到答案;
【详解】(1)解:由数轴可得,
,
∴,,,
故答案为:<,<,>;
(2)解:由(1)可得,
原式
.
【点睛】本题考查数轴上点之间关系,有理数加减运算法则,绝对值的性质,解题的关键是根据数轴得到式子与0的关系.
5.(1)详见解析
(2)
(3)
【分析】(1)直接在数轴上标出,即可求解;
(2)直接观察数轴,即可求解;
(3)根据题意可得,再根据绝对值的性质化简,再合并,即可求解.
【详解】(1)解:在数轴上表示.如图:
(2)解:把这五个数从小到大用“”连接起来如下:
;
(3)解:∵,
∴,
原式
【点睛】本题主要考查了数轴,就绝对值的性质,整式的加减混合运算,利用数形结合思想解答是解题的关键.
6.(1),,
(2)
【分析】(1)根据a、b、c在数轴上的位置,即可判定它们的正负及绝对值的大小,据此即可解答;
(2)根据(1)中的结论,化简绝对值,再进行整式的加减运算,即可求得结果.
【详解】(1)解:由图可知,,,且,
所以,,;
故答案为:,,;
(2)解:,,,
.
【点睛】本题考查了利用数轴判断式子的符号,化简绝对值符号,整式的加减运算,准确判断出各式子的符号是解决本题的关键.
7.(1),,
(2)
【分析】(1)根据各点在数轴上的位置上判断出其符号及绝对值的大小,进而可得出结论;
(2)根据(1)中的结论去绝对值符号,合并同类项即可.
【详解】(1)解:∵由有理数a、b、c在数轴上的位置可知,,,
∴,,.
故答案为:,,;
(2)
【点睛】本题考查的是有理数的大小比较,熟知数轴上右边的数比左边的大是解题的关键.
8.(1)a<0<c<﹣b
(2)c﹣b
【分析】(1)根据各点在数轴上的位置判断出a、b、c的符号及绝对值的大小,再从左到右用“<”连接起来即可
(2)根据(1)中a、b、c的符号判断出各式的符号,再去绝对值符号,合并同类项即可.
【详解】(1)解:画出在数轴上的位置如图:
由图可知,,
;
(2)由(1)可知,,
,,,
原式,
,
.
【点睛】本题考查的是有理数的大小比较,熟知数轴上右边的数总比左边的大是解题的关键.
9.(1)|a|=a,|b|=﹣b,|c|=﹣c;(2)﹣a<a<﹣c;(3)﹣2c.
【分析】(1)根据图示可知c
(3)根据题意得:a+b=0,a﹣b>0,a+c<0,b﹣c>0,由此进行化简即可得结果.
【详解】(1)∵从数轴可知:c<b<0<a,
∴|a|=a,|b|=﹣b,|c|=﹣c;
(2)∵从数轴可知:c<b<0<a,|c|>|a|,
∴﹣a<a<﹣c;
(3)根据题意得:a+b=0,a﹣b>0,a+c<0,b﹣c>0,
则|a+b|+|a﹣b|+|a+c|+|b﹣c|
=0+a-b﹣a﹣c+b-c
=﹣2c.
【点睛】本题考查了数轴、绝对值的化简、有理数大小比较等,读懂数轴、熟练应用相关知识是解题的关键.
10.(1)
(2)
【分析】(1)先判断再结合相反数,有理数的减法运算可得答案;
(2)由再根据化简绝对值的法则化简绝对值,再合并即可.
【详解】(1)解:∵
∴
故答案为:.
(2)结合(1)可得:
【点睛】本题考查的是利用数轴比较有理数的大小,绝对值的含义,化简绝对值,有理数的减法法则的理解,去括号,合并同类项,掌握“绝对值的化简方法”是解本题的关键.
11.(1)
(2)
【分析】(1)先乘除,再进行加法运算;
(2)先乘方,再乘除,最后算减法.
【详解】(1)解:原式
;
(2)原式
.
【点睛】本题考查有理数的混合运算,熟练掌握有理数的运算法则,是解题的关键.
12.(1);
(2).
【分析】(1)用有理数的加法的法则和减法的法则从左到右依次计算;
(2)先用有理数乘方的法则计算乘方,再用有理数的乘法的法则和除法的法则计算乘除,最后用有理数的加法的法则和减法的法则计算加减.
【详解】(1)解:
(2)
【点睛】本题主要考查了有理数的混合运算,解决问题的关键是熟练掌握混合运算的顺序,乘方、乘除、加减的运算法则.
13.(1)5;
(2)0.
【分析】(1)根据有理数的加减法可以解答本题;
(2)先算乘方,再算乘除法,最后算加减,可以解答本题.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查了有理数的混合运算,有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
14.(1);
(2).
【分析】(1)根据有理数的加减运算,求解即可;
(2)根据有理数的乘方以及四则混合运算,求解即可.
【详解】(1)解:;
(2)解:
.
【点睛】此题考查了有理数的乘方以及四则混合运算,解题的关键是熟练掌握有理数的有关运算法则.
15.(1)
(2)
【分析】(1)根据有理数的加减混合运算进行计算即可求解;
(2)根据有理数的混合运算进行计算即可求解.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查了有理数的混合运算,掌握有理数的运算法则是解题的关键.
16.(1)
(2)
【分析】(1)根据有理数的加减进行计算即可求解;
(2)根据有理数的混合运算进行计算即可求解.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查了有理数的混合运算,掌握有理数的运算法则是解题的关键.
17.(1)-8
(2)-1
【分析】(1)原式先去括号,再计算即可得到答案.
(2)原式先计算乘方,再计算乘除、去绝对值,最后进行加减运算即可求解.
【详解】(1)原式
.
(2)原式
.
【点睛】此题考查了有理数的混合运算,熟练掌握运算法则是本题的关键.
18.(1)
(2)0
【分析】(1)先计算乘方,同时根据乘法分配律进行计算即可求解;
(2)根据有理数的混合运算顺序进行计算即可求解.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查了有理数的混合运算,掌握有理数的运算顺序以及有理数的运算法则是解题的关键.
19.(1)9
(2)6
【分析】(1)根据有理数的混合运算法则计算即可;
(2)根据有理数的混合运算法则计算即可.
【详解】(1)
;
(2)
.
【点睛】本题考查了有理数的四则混合,掌握有理数的四则混合运算法则是解答本题的关键.
20.(1)
(2)
【分析】(1)根据有理数四则混合运算法则进行计算即可;
(2)根据含乘方的有理数混合运算法则进行计算即可.
【详解】(1)解:
;
(2)解:
.
【点睛】本题主要考查了有理数混合运算,解题的关键是熟练掌握运算法则,准确计算.
21.(1);
(2).
【分析】(1)根据乘法分配律简便计算;
(2)根据有理数的乘方、有理数的乘除法和加减法可以解答本题.
【详解】(1)解:
;
(2)解:
.
【点睛】本题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,注意乘法运算定律的应用.
22.(1)1
(2)8
(3)
【分析】(1)根据有理数的加减法可以解答本题;
(2)先算乘方,再算乘法,最后算加减;如果有括号,要先做括号内的运算;
(3)先把除法运算转化成乘法运算,再根据乘法分配律计算.
【详解】(1)解:
;
(2)解:
;
(3)解:
.
【点睛】本题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,注意乘法运算定律的应用.
23.(1)7
(2)5
【分析】(1)先算乘方,再算乘除法,最后算加减法即可;
(2)先算乘方和括号内的式子,再算乘除法,最后算加减法即可.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查了含有乘方的有理数混合运算,熟练掌握运算法则和运算顺序是解题的关键.
24.(1)49
(2)13
【分析】(1)先算乘方,把除法转为乘法,再算乘法,最后算加法即可;
(2)先算乘法,再算加减即可.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查的是有理数的混合运算,需要熟练掌握有理数的混合运算法则.
25.(1)
(2)
【分析】(1)先计算有理数的乘方,再根据有理数的混合运算法则计算即可;
(2)根据乘法分配律计算即可.
【详解】(1)解:
;
(2)
.
【点睛】本题考查了有理数的混合运算,解题的关键是掌握有理数的混合运算顺序和法则.
26.(1)
(2)3
【分析】(1)先算第2项括号里的,除法转换为乘法,再根据乘法分配律展开,最后计算加减即可;
(2)先算乘方,化简绝对值,根据法则进一步处理.
【详解】(1)解:
;
(2)
.
【点睛】本题考查有理数的混合运算,注意运算中符号的处理,掌握运算法则是解题的关键.
27.(1)1
(2)25
【分析】(1)先把分数化成小数,然后再利用有理数加减运算法则计算即可;
(2)直角运用乘法结合律计算即可.
【详解】(1)解:
=
=
=-7+8
=1.
(2)解:
=
=
=25.
【点睛】本题主要考查了有理数的加减混合运算、乘法结合律等知识点,灵活应用相关运算法则和运算律成为解答本题的关键.
28.(1)
(2)
【分析】(1)先算乘法,再算加减法即可;
(2)先算乘方和括号内的式子,然后算乘法,最后算减法即可.
【详解】(1)解:
;
(2)解:
.
【点睛】本题考查的是有理数的混合运算,熟练掌握有理数的混合运算法则是解题的关键.
29.(1)
(2)2
【分析】对于(1),先将小数变为分数,同时去括号,再根据有理数的加减法法则计算即可;
对于(2),先算乘方,同时计算括号内的,再计算乘除法,最后计算加减.
【详解】(1)原式
;
(2)原式
.
【点睛】本题主要考查了有理数的混合运算,掌握运算法则是解题的关键.即先算乘方,再算乘除,最后算加减,有括号的先计算括号内的.
30.(1)8
(2)
【分析】根据先乘方,再算乘除法,最后再算加减的有理数混合运算顺序进行计算即可.
【详解】(1)解:原式
;
(2)解:原式
.
【点睛】本题考查了含乘方的有理数的混合运算,熟练掌握有理数的混合运算顺序是计算本题的关键.
答案第16页,共17页
答案第17页,共17页
