第十一章 第03讲多边形及其内角和 同步学与练(含解析)2023-2024学年八年级数学上册人教版
文档属性
| 名称 | 第十一章 第03讲多边形及其内角和 同步学与练(含解析)2023-2024学年八年级数学上册人教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 00:00:00 | ||
图片预览



文档简介
第03讲 多边形及其内角和
课程标准 学习目标
①多边形的认识 ②多边形的内角和与外角和 ③正多边形 掌握多边形及其与多边形有关的概念. 掌握多边形的内角和计算公式,内角和公式的推导过程及其相关计算,掌握多边形的外角和度数. 掌握正多边形的概念,且根据正多边形的性质解决相应的题目.
知识点01 多边形的认识
1.形的概念:
在平面内,由多条线段首位顺次连接所组成的图形是多边形.组成的线段有多少条,则图形就是一个几边形.
2.形的相关概念:
如图:组成多边形的线段叫做多边形的边;相邻两条边的交点叫多边形的顶点;相邻两条边构成的角是多边形的内角;任意两个不相邻的顶点间的连线段叫做多边形的对角线;多边形的边与邻边的延长线构成的角叫做多边形的外角.
题型考点:判断图形.
【即学即练1】
1.如图所示的图形中,属于多边形的有
A.3个 B.4个 C.5个 D.6个
知识点02 多边形的内角和外角和
1.形的对角线计算:
总结规律:若多边形的边数为,则多边形一个顶点的对角线条数为条,多边形所有的对角线条数为条.
2.形一个顶点的对角线把多边形分成的三角形数量计算:
由上图总结:一个顶点的对角线分多边形成三角形的个数为:个.
3.形的内角和计算公式:
由上图可知,多边形的内角和等于图中所有三角形的内角和之和.即:.
4.形的外角和:
任意多边形的外角和都等于.
题型考点:
①利用内角和公式求内角和或求多边形的边数.
②利用多边形的内外角关系计算.
【即学即练1】
2.十二边形的内角和是( )
A.1440° B.1620° C.1800° D.1980°
3.若一个多边形的内角和是1080°,则这个多边形的边数是( )
A.6 B.7 C.8 D.10
【即学即练2】
4.多边形的边数由3增加到2021时,其外角和的度数( )
A.增加 B.减少 C.不变 D.不能确定
【即学即练3】
5.一个多边形的内角和比它的外角和的3倍少180°,则这个多边形的边数是 .
6.若一个多边形的内角和比外角和大360°,则这个多边形的边数为 .
知识点03 正多边形
1.边形的概念:
每条边都相等,每个内角都相等的多边形是正多边形.
2.边形的每个内角计算:
因为正多边形的内角和为,每个内角都相等且有个内角,所以正多边形的每个内角度数为:.
3.边形的每个外角计算:
正多边形的外角和是360°,每个外角也相等,所以正多边形的每个外角度数为.
4.多边形的内角与外角关系:
;
题型考点:利用正多边形的相关计算公式计算.
【即学即练1】
7.若一个多边形的每个内角都为,则它的边数为( )
A.6 B.8 C.5 D.10
8.一个多边形的每一个外角都等于,那么这个多边形的内角和是 °.
9.如果一个正多边形的一个内角与一个外角的度数之比是,那么这个正多边形的边数是( )
A.11 B.10 C.9 D.8
题型01 多边形的截角问题
【典例1】
10.在中,,沿图中虚线截去,则( )
A. B. C. D.
变式1:
11.一个多边形截去一个角(不过顶点)后,所成的一个多边形的内角和是2520°,那么原多边形的边数是( )
A.13 B.15 C.17 D.19
变式2:
12.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )
A.10 B.11 C.12 D.10或11或12
变式3:
13.一个多边形截去一个角后,形成的另一个多边形的内角和是1440°.则原来多边形的边数是 .
题型02 实际生活与正多边形
【典例1】
14.点出发向前直走,向左转,继续向前走,再向左转,他以同样的走法回到点时,共走了 .
变式1:
15.如图,小明从点A出发沿直线前进10米到达点B,向左转后又沿直线前进10米到达点C,再向左转后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为( )
A.100米 B.80米 C.60米 D.40米
【典例2】
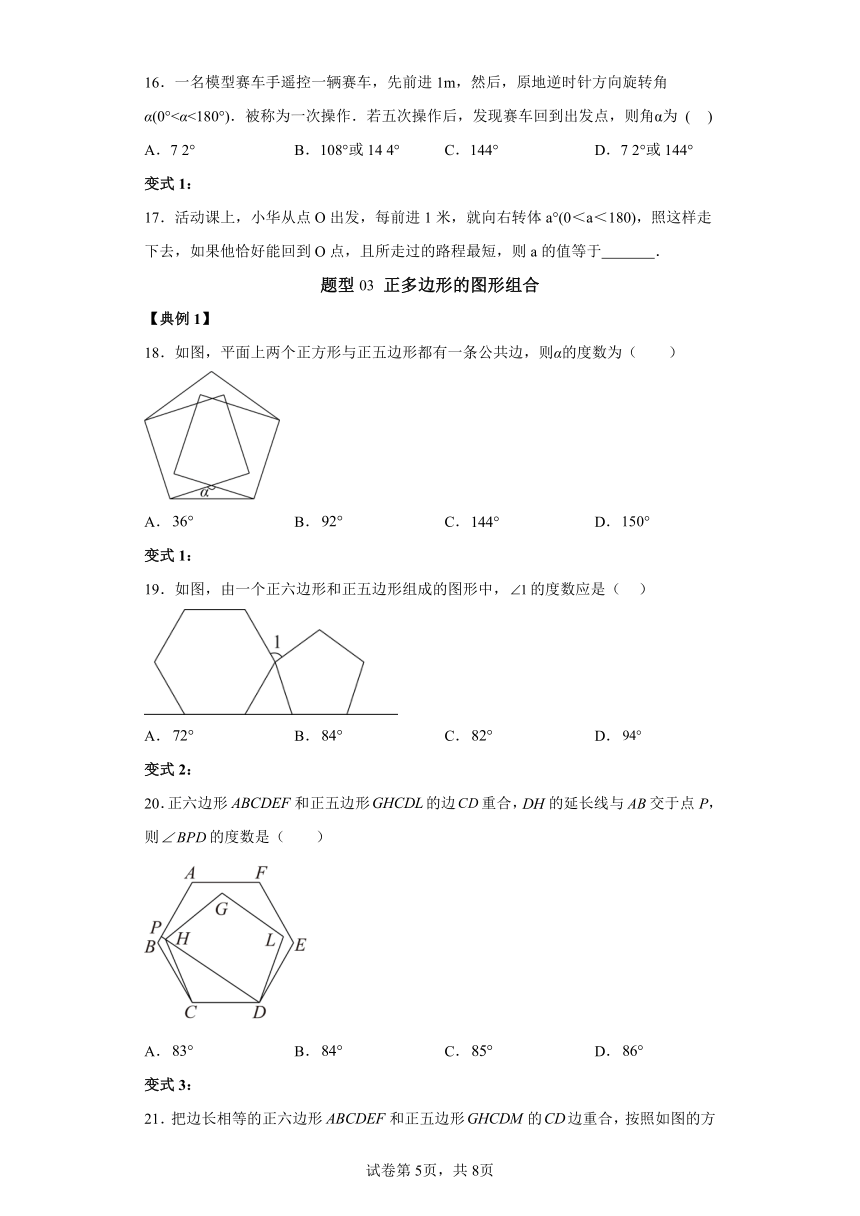
16.一名模型赛车手遥控一辆赛车,先前进1m,然后,原地逆时针方向旋转角α(0°<α<180°).被称为一次操作.若五次操作后,发现赛车回到出发点,则角α为 ( )
A.7 2° B.108°或14 4° C.144° D.7 2°或144°
变式1:
17.活动课上,小华从点O出发,每前进1米,就向右转体a°(0<a<180),照这样走下去,如果他恰好能回到O点,且所走过的路程最短,则a的值等于 .
题型03 正多边形的图形组合
【典例1】
18.如图,平面上两个正方形与正五边形都有一条公共边,则α的度数为( )
A. B. C. D.
变式1:
19.如图,由一个正六边形和正五边形组成的图形中,的度数应是( )
A. B. C. D.
变式2:
20.正六边形和正五边形的边重合,的延长线与交于点P,则的度数是( )
A. B. C. D.
变式3:
21.把边长相等的正六边形和正五边形的边重合,按照如图的方式叠合在一起,延长交于点N,则等于( )
A. B. C. D.
22.八边形的内角和是外角和的( )倍
A.2 B.3 C.4 D.5
23.下列角度不可能是多边形内角和的为( )
A. B. C. D.
24.如图,的度数是( )
A. B. C. D.
25.清明节当天八年级某班组织学生去烈士林园为革命先烈扫墓,以此表达对先烈的追思和崇敬之情,细心的小明发现革命烈士纪念塔的塔底平面为八边形,这个八边形的内角和为( )
A. B. C. D.
26.如图,四边形为一矩形纸带,点E、F分别在边、上,将纸带沿折叠,点A、D的对应点分别为、,若,则的度数为( )
A.62.5° B.72.5° C.55° D.45°
27.如图,奇奇先从点出发前进,向右转,再前进,又向右转,…,这样一直走下去,他第一次回到出发点时,一共走了( )
A. B. C. D.
28.若一个正多边形每一个外角都相等,且一个内角的度数是,则这个多边形是( )
A.正七边形 B.正八边形 C.正九边形 D.正十边形
29.如图,在五边形中,,,,则的度数是( )
A. B. C. D.
30.如图所示,则的度数是 .
31.如图,正五边形的对角线、相交于点F,则的度数为 .
32.如图,四边形中,与的角平分线相交于点P,若,则 °.
33.将正六边形与正方形按如图所示摆放,且正六边形的边与正方形的边在同一条直线上,则的度数是 .
34.(1)正八边形的每个内角是每个外角的倍,求的值;
(2)一个多边形的外角和是内角和的,求这个多边形的边数.
35.已知,如图,AD与BC交于点O.
(1)如图1,判断与的数量关系:_______,并证明你的结论.
(2)如图2,的度数为______.
(3)如图3,若平分,平分,与交于点M.,请直接写出_____.
36.如图,四边形中,,平分,,交于点.
(1)如图1,若,
①求证:;
②作平分,如图2,求证:.
(2)如图3,作平分,在锐角内部作射线,交于,若的大小为,试说明:平分.
试卷第8页,共8页
试卷第1页,共8页
参考答案:
1.A
【详解】解:根据多边形的定义:平面内不在同一条直线上的几条线段首尾顺次相接组成的图形叫多边形.显然只有第一个、第二个、第五个符合题意.
故选A.
2.C
【分析】由多边形内角和公式(n-2)×180°计算即可.
【详解】由多边形内角和=(n-2)180°,其中n为多边形的边数.
所以12边形的内角和=(12-2)×180°=1800°.
故答案为:C
【点睛】本题主要考查多边形内角和公式,正确认识公式中的n为多边形的边数,直接代入计算即可解决.
3.C
【分析】多边形的内角和可以表示成(n2) 180°,依此列方程可求解.
【详解】解:设所求多边形边数为n,则
1080°=(n2) 180°,
解得:n=8.
故选:C.
【点睛】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
4.C
【分析】根据多边形的外角和定理即可求解判断.
【详解】解:∵任何多边形的外角和都是360°,
∴多边形的边数由3增加到2021时,其外角和的度数不变,
故选:C.
【点睛】此题考查多边形的外角和,熟记多边形的外角和是360度,并不随边数的变化而变化是解题的关键.
5.7
【分析】多边形的内角和可以表示成(n-2) 180°,外角和都等于360°,故可列方程求解.
【详解】解:设所求多边形边数为n,
则(n-2) 180°=3×360°-180°,
解得n=7.
故答案为:7.
【点睛】本题考查了多边形内角与外角,关键是根据多边形的内角和和外角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
6.6
【详解】设多边形的边数是,
根据题意得,,
解得.
故答案为:6.
7.B
【分析】根据邻补角关系,求得多边形的外角度数,用多边形的外角和定理计算即可.
【详解】解:∵一个正多边形的每个内角都为,
∴这个正多边形的每个外角都为:,
∴这个多边形的边数为:.
故选:B.
【点睛】本题考查了已知多边形的内角求边数,熟练将内角度数转化为外角度数是解题的关键.
8.1440
【分析】由多边形外角的性质可求解多边形的边数,再利用多边形的内角和定理可求解.
【详解】解:,
.
即这个多边形的内角和是,
故答案为:.
【点睛】本题主要考查多边形的内角与外角,求解多边形的边数是解题的关键.
9.C
【分析】设这个正多边形的边数为n,由“如果一个正多边形的一个内角与一个外角的度数之比是7:2”,得出此多边形的外角和为(n-2)×180°,又根据多边形的外角和为360°,由此列出方程,解方程即可.
【详解】解:设这个正多边形的边数为n,
由题意得:(n-2)×180=360,
解得:n=9,
故选:C.
【点睛】此题考查了多边形的内角和与外角和,熟记多边形的内角和公式及多边形的外角和是360°是解题的关键.
10.C
【分析】可先求得的度数,根据四边形内角和为,即可求得答案.
【详解】∵,
∴.
∴.
故选:C.
【点睛】本题主要考查多边形内角和,牢记多边形内角和公式(边形内角和等于)是解题的关键.
11.B
【分析】一个多边形截去一个角(截线不过顶点)之后,则多边形的角增加了一个,求出内角和是2520°的多边形的边数,即可求得原多边形的边数.
【详解】解:设内角和是2520°的多边形的边数是n.
根据题意得:(n-2) 180=2520,
解得:n=16.
则原来的多边形的边数是16-1=15.
故选:B.
【点睛】本题主要考查了多边形的内角和公式,理解新多边形的边数比原多边形的边数增加1是解题的关键.
12.D
【分析】先根据多边形的内角和公式求出截去一个角后的多边形的边数,再根据截去一个角后边数增加1,不变,减少1讨论得解.
【详解】解:设多边形截去一个角的边数为n,
则(n﹣2) 180°=1620°,
解得n=11,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是10或11或12.
故选:D.
【点睛】本题考查了多边形的内角和公式,本题难点在于多边形截去一个角后边数有增加1,不变,减少1三种情况.
13.9或10或11
【分析】先根据多边形的内角和公式求出截去一个角后的多边形的边数,再分情况说明求得原来多边形的解.
【详解】解:设多边形截去一个角的边数为,根据题意得:
又截去一个角后的多边形的边可以增加1、不变、减少1,
原多边形的边数为9或10或11.
【点睛】本题考查的是多边形的内角和公式,本题的易错点在于忽略考虑截去一个角后多边形的边数可以不变、增加或者减少.
14.
【分析】根据题意,小聪走过的路是正多边形,先用除以求出边数,然后再乘以米即可.
【详解】解:∵多边形的边数为,
∴小华要走次才能回到原地,
∴小华走的距离为.
故答案为:.
【点睛】此题考查了多边形的外角和定理,解题的关键是熟记任何一个多边形的外角和都是.
15.B
【分析】根据题意,小明走过的路程是正多边形,先用360°除以45°求出边数,然后再乘以10米即可.
【详解】解:∵小明每次都是沿直线前进10米后再向左转,
∴他走过的图形是正多边形,边数n=360°÷45°=8,
∴小明第一次回到出发点A时所走的路程=8×10=80米.
故选:B.
【点睛】本题考查了正多边形外角问题的实际应用,根据题意判断小明走过的图形是正多边形是解题的关键.
16.D
【分析】因为赛车五次操作后回到出发点,五次操作一种是“正五边形“二种是“五角星“形,根据α最大值小于180°,经过五次操作,绝对不可能三圈或三圈以上.一圈360°或两圈720度.分别用360°和720°除以5,就可以得到答案.
【详解】解:360÷5=72°,
720÷5=144°.
故选D.
【点睛】本题主要考查了正多边形的外角的特点.正多边形的每个外角都相等.
17.120
【详解】解:根据题意,小华所走过的路线是正多边形,
∴边数,
走过的路程最短,则n最小,a最大,
n最小是3,a°最大是120°.
18.C
【分析】根据正五边形和正方形的内角的度数进行计算即可.
【详解】解:如图,∵正五边形的每个内角是,正方形的每个内角,
,
,
故选:C.
【点睛】本题考查了多边形的内角,掌握正五边形和正方形的内角是解题的关键.
19.B
【分析】根据正多边形内角和公式求出正六边形和正五边形的内角和内角的补角,结合三角形内角和定理即可求解;
【详解】解:正六边形的内角为:,内角的补角为:60°;
正五边形的内角为:,内角的补角为:72°;
∴
故选:B
【点睛】本题主要考查多边形内角和公式,三角形的内角和定理,掌握相关知识并正确求解是解题的关键.
20.B
【分析】先根据正多边形的内角和求出,,进而求出 ,再根据四边形的内角和求出答案.
【详解】解:∵六边形为正六边形,
∴.
∵五边形为正五边形,
∴,,
∴.
∵四边形的内角和为,
∴.
故选:B.
【点睛】本题主要考查了多边形的内角和定理,掌握多边形内角和公式是解题的关键.
21.B
【分析】根据正六边形的性质求得、、的度数,根据正五边形的性质求得、的度数,然后再由六边形的内角和求得.
【详解】解:∵六边形,
∴,
∵五边形是正五边形,
∴,
∵,
∴,
故选:B.
【点睛】本题主要考查了正多边形的性质应用,准确计算是解题的关键.
22.B
【分析】根据多边形的内角和公式求得八边形的内角和,然后与多边形的外角和为360°作商即可.
【详解】解:∵八边形的内角和为:,其外角和为,
(倍),
故选:B.
【点睛】本题考查多边形的内角和与外角和,此为基础且重要知识点,必须熟练掌握.
23.B
【分析】设多边形的边数为且为整数),然后利用多边形的内角和公式,结合各项列得方程,解方程求得值,判断值是否符合题意即可.
【详解】解:设多边形的边数为且为整数),
则,
解得:,则A不符合题意;
,
解得:,则B符合题意;
,
解得:,则C不符合题意;
,
解得:,则D不符合题意;
故选:B.
【点睛】本题考查多边形的内角和公式,此为基础且重要知识点,必须熟练掌握.
24.A
【分析】首先根据三角形内角和定理和对顶角得到,然后代入求解即可.
【详解】解:∵,,
∴
∴
,
故选:A.
【点睛】本题主要考查三角形的内角和定理,多边形内角和,对顶角的性质,掌握相关定理是解题的关键.
25.C
【分析】直接利用多边形的内角和公式进行计算即可.
【详解】解:这个八边形的内角和为:;
故选C
【点睛】本题考查的是多边形的内角和定理的应用,熟记多边形内角和公式是解本题的关键.
26.B
【分析】如图,折叠得到,平角的定义,得到,平行线的性质,得到,即可得解.
【详解】解:如图,
∵将纸带沿折叠,点A、D的对应点分别为、,
∴,
∵四边形为一矩形纸带,
∴,
∴,
故选B.
【点睛】本题考查矩形与折叠.解题的关键是掌握矩形的性质,折叠的性质.
27.D
【分析】由题意可知奇奇所走的路线为正多边形,根据多边形的外角和定理即可求出答案.
【详解】解:∵奇奇从A点出发最后回到出发点A时正好走了一个正多边形,
∴根据外角和定理可知正多边形的边数为,
则一共走了米.
故选D.
【点睛】本题主要考查了多边形外角和定理的应用,解题的关键是判断出奇奇所走的路线为正多边形,牢记任何一个多边形的外角和都是,正多边形的每一个外角都相等.
28.C
【分析】由多边形的内角与外角互补求得外角的度数,再由正多边形的外角和为,可得到答案.
【详解】解:∵一个内角的度数是,
∴每个外角度数为,
∴正多边形的边数为:,
即这个多边形是正九边形.
故选C.
【点睛】本题考查正多边形的外角和,熟练掌握正多边形的性质是解题的关键.
29.C
【分析】利用多边形的内角和公式可得五边形的内角和,由平行线的性质可得,从而得到,利用邻补角的定义可得,从而得出,进行计算即可得出的度数.
【详解】解:四边形为五边形,
其内角和为,
,
,
,
,
,
,
,
故选:C.
【点睛】本题主要考查多边形的内角和,平行线的性质,邻补角的定义,熟练掌握多边形的内角和公式,平行线的性质,邻补角的定义,是解题的关键.
30.##360度
【分析】如图所示,与交于点,连接,根据三角形的外角和的性质可得,,由此可将转化为求四边形的内角和,由此即可求解.
【详解】解:如图所示,与交于点,连接,
∴在中,,
在中,,
∴,
∵,,
∴,
∵四边形的内角和为,
∴,
故答案为:.
【点睛】本题主要考查三角形的外角和的性质,四边形的内角和定理,掌握以上知识是解题的关键.
31.##108度
【分析】先根据正多边形内角和公式求出内角的度数,再根据等腰三角形的性质求出,,最后根据三角形内角和定理得出答案.
【详解】解:∵五边形为正五边形,
∴,,
∴,
∴.
故答案为:108°.
【点睛】本题主要考查了多边形内角和定理,三角形内角和定理,掌握多边形内角和计算公式是解题的关键.
32.13
【分析】延长交于点D,与交于点E,根据三角形外角性质和三角形内角和定理计算即可.
【详解】解:延长交于点D,与交于点E,
根据三角形的外角的性质,
,,
∵与的角平分线相交于点P,
∴,
∴,
根据三角形的内角和定理,
,
∴,
∴,
∵,
所以,
故答案为:13.
【点睛】本题考查了角的平分线计算,三角形外角性质,三角形内角和定理,熟练掌握外角性质和角的平分线的意义是解题的关键.
33.##度
【分析】先根据多边形的内角和共求出六边形的内角,然后根据正多边形内角与外角的互补即可求得正六边形和正方形的外角,最后根据三角形的内角和即可求得的度数.
【详解】解:∵图中六边形为正六边形,
∴,
∴,
∵正方形中,,
∴,
∴,
故答案为:.
【点睛】此题考查了正多边形的内角和公式,正多边形的外角与内角的互补,熟记正多边形的内角和公式是解题的关键.
34.(1);(2)十四边形
【分析】(1)分别求出正八边形的每个内角和外角的度数,即可求解;
(2)设这个多边形的边数为,根据题意,列出方程,即可求解.
【详解】解:(1)∵正八边形的每个内角,正八边形的每个外角,
∴;
(2)设这个多边形的边数为,根据题意得:,
解得.
∴这个多边形是十四边形.
【点睛】此题考查多边形内角与外角,正确的列出方程组是解题的关键.
35.(1),证明见解析
(2)
(3)
【分析】(1)根据三角形的内角和定理和对顶角相等即可得出结论;
(2)连接,由(1)可得,则等于五边形内角和;
(3)根据(1)中结论即可求解.
【详解】(1)解:,证明如下:
证明:∵,且,
∴;
故答案为:;
(2)解:连接,
由(1)可得,
∴,
∴五边形内角和,
故答案为:.
(3)解:由(1)中结论可得:,
∵,
∴,
∵平分,平分,
∴,
∴,
由(1)中结论可得:,
故答案为:.
【点睛】本题主要考查了三角形的内角和,多边形的内角和,对顶角相等,解题的关键是掌握三角形的内角和为,多边形内角和为.
36.(1)①见解析 ②见解析
(2)见解析
【分析】(1)①根据多边形内角和可证得,结合,即可得到结论.②根据角平分线的定义可求得,结合,可证得,即可得到结论.
(2)延长,交于点,可先证得,结合,,可求得.
【详解】(1)①∵,,
∴.
∵,
∴.
②∵平分,
∴.
∵平分,
∴.
∴.
∵,
∴.
∴.
∴.
(2)延长,交于点,如图所示:
∵,
∴.
∴.
∵平分,
∴.
∵平分,
∴.
∵,
∴.
∴.
∴.
∴平分.
【点睛】本题主要考查角平分线的定义、三角形的外角的性质、多边形内角和、平行线的判定,能根据题意构建辅助线是解题的关键.
答案第12页,共15页
答案第11页,共15页
课程标准 学习目标
①多边形的认识 ②多边形的内角和与外角和 ③正多边形 掌握多边形及其与多边形有关的概念. 掌握多边形的内角和计算公式,内角和公式的推导过程及其相关计算,掌握多边形的外角和度数. 掌握正多边形的概念,且根据正多边形的性质解决相应的题目.
知识点01 多边形的认识
1.形的概念:
在平面内,由多条线段首位顺次连接所组成的图形是多边形.组成的线段有多少条,则图形就是一个几边形.
2.形的相关概念:
如图:组成多边形的线段叫做多边形的边;相邻两条边的交点叫多边形的顶点;相邻两条边构成的角是多边形的内角;任意两个不相邻的顶点间的连线段叫做多边形的对角线;多边形的边与邻边的延长线构成的角叫做多边形的外角.
题型考点:判断图形.
【即学即练1】
1.如图所示的图形中,属于多边形的有
A.3个 B.4个 C.5个 D.6个
知识点02 多边形的内角和外角和
1.形的对角线计算:
总结规律:若多边形的边数为,则多边形一个顶点的对角线条数为条,多边形所有的对角线条数为条.
2.形一个顶点的对角线把多边形分成的三角形数量计算:
由上图总结:一个顶点的对角线分多边形成三角形的个数为:个.
3.形的内角和计算公式:
由上图可知,多边形的内角和等于图中所有三角形的内角和之和.即:.
4.形的外角和:
任意多边形的外角和都等于.
题型考点:
①利用内角和公式求内角和或求多边形的边数.
②利用多边形的内外角关系计算.
【即学即练1】
2.十二边形的内角和是( )
A.1440° B.1620° C.1800° D.1980°
3.若一个多边形的内角和是1080°,则这个多边形的边数是( )
A.6 B.7 C.8 D.10
【即学即练2】
4.多边形的边数由3增加到2021时,其外角和的度数( )
A.增加 B.减少 C.不变 D.不能确定
【即学即练3】
5.一个多边形的内角和比它的外角和的3倍少180°,则这个多边形的边数是 .
6.若一个多边形的内角和比外角和大360°,则这个多边形的边数为 .
知识点03 正多边形
1.边形的概念:
每条边都相等,每个内角都相等的多边形是正多边形.
2.边形的每个内角计算:
因为正多边形的内角和为,每个内角都相等且有个内角,所以正多边形的每个内角度数为:.
3.边形的每个外角计算:
正多边形的外角和是360°,每个外角也相等,所以正多边形的每个外角度数为.
4.多边形的内角与外角关系:
;
题型考点:利用正多边形的相关计算公式计算.
【即学即练1】
7.若一个多边形的每个内角都为,则它的边数为( )
A.6 B.8 C.5 D.10
8.一个多边形的每一个外角都等于,那么这个多边形的内角和是 °.
9.如果一个正多边形的一个内角与一个外角的度数之比是,那么这个正多边形的边数是( )
A.11 B.10 C.9 D.8
题型01 多边形的截角问题
【典例1】
10.在中,,沿图中虚线截去,则( )
A. B. C. D.
变式1:
11.一个多边形截去一个角(不过顶点)后,所成的一个多边形的内角和是2520°,那么原多边形的边数是( )
A.13 B.15 C.17 D.19
变式2:
12.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )
A.10 B.11 C.12 D.10或11或12
变式3:
13.一个多边形截去一个角后,形成的另一个多边形的内角和是1440°.则原来多边形的边数是 .
题型02 实际生活与正多边形
【典例1】
14.点出发向前直走,向左转,继续向前走,再向左转,他以同样的走法回到点时,共走了 .
变式1:
15.如图,小明从点A出发沿直线前进10米到达点B,向左转后又沿直线前进10米到达点C,再向左转后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为( )
A.100米 B.80米 C.60米 D.40米
【典例2】
16.一名模型赛车手遥控一辆赛车,先前进1m,然后,原地逆时针方向旋转角α(0°<α<180°).被称为一次操作.若五次操作后,发现赛车回到出发点,则角α为 ( )
A.7 2° B.108°或14 4° C.144° D.7 2°或144°
变式1:
17.活动课上,小华从点O出发,每前进1米,就向右转体a°(0<a<180),照这样走下去,如果他恰好能回到O点,且所走过的路程最短,则a的值等于 .
题型03 正多边形的图形组合
【典例1】
18.如图,平面上两个正方形与正五边形都有一条公共边,则α的度数为( )
A. B. C. D.
变式1:
19.如图,由一个正六边形和正五边形组成的图形中,的度数应是( )
A. B. C. D.
变式2:
20.正六边形和正五边形的边重合,的延长线与交于点P,则的度数是( )
A. B. C. D.
变式3:
21.把边长相等的正六边形和正五边形的边重合,按照如图的方式叠合在一起,延长交于点N,则等于( )
A. B. C. D.
22.八边形的内角和是外角和的( )倍
A.2 B.3 C.4 D.5
23.下列角度不可能是多边形内角和的为( )
A. B. C. D.
24.如图,的度数是( )
A. B. C. D.
25.清明节当天八年级某班组织学生去烈士林园为革命先烈扫墓,以此表达对先烈的追思和崇敬之情,细心的小明发现革命烈士纪念塔的塔底平面为八边形,这个八边形的内角和为( )
A. B. C. D.
26.如图,四边形为一矩形纸带,点E、F分别在边、上,将纸带沿折叠,点A、D的对应点分别为、,若,则的度数为( )
A.62.5° B.72.5° C.55° D.45°
27.如图,奇奇先从点出发前进,向右转,再前进,又向右转,…,这样一直走下去,他第一次回到出发点时,一共走了( )
A. B. C. D.
28.若一个正多边形每一个外角都相等,且一个内角的度数是,则这个多边形是( )
A.正七边形 B.正八边形 C.正九边形 D.正十边形
29.如图,在五边形中,,,,则的度数是( )
A. B. C. D.
30.如图所示,则的度数是 .
31.如图,正五边形的对角线、相交于点F,则的度数为 .
32.如图,四边形中,与的角平分线相交于点P,若,则 °.
33.将正六边形与正方形按如图所示摆放,且正六边形的边与正方形的边在同一条直线上,则的度数是 .
34.(1)正八边形的每个内角是每个外角的倍,求的值;
(2)一个多边形的外角和是内角和的,求这个多边形的边数.
35.已知,如图,AD与BC交于点O.
(1)如图1,判断与的数量关系:_______,并证明你的结论.
(2)如图2,的度数为______.
(3)如图3,若平分,平分,与交于点M.,请直接写出_____.
36.如图,四边形中,,平分,,交于点.
(1)如图1,若,
①求证:;
②作平分,如图2,求证:.
(2)如图3,作平分,在锐角内部作射线,交于,若的大小为,试说明:平分.
试卷第8页,共8页
试卷第1页,共8页
参考答案:
1.A
【详解】解:根据多边形的定义:平面内不在同一条直线上的几条线段首尾顺次相接组成的图形叫多边形.显然只有第一个、第二个、第五个符合题意.
故选A.
2.C
【分析】由多边形内角和公式(n-2)×180°计算即可.
【详解】由多边形内角和=(n-2)180°,其中n为多边形的边数.
所以12边形的内角和=(12-2)×180°=1800°.
故答案为:C
【点睛】本题主要考查多边形内角和公式,正确认识公式中的n为多边形的边数,直接代入计算即可解决.
3.C
【分析】多边形的内角和可以表示成(n2) 180°,依此列方程可求解.
【详解】解:设所求多边形边数为n,则
1080°=(n2) 180°,
解得:n=8.
故选:C.
【点睛】本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
4.C
【分析】根据多边形的外角和定理即可求解判断.
【详解】解:∵任何多边形的外角和都是360°,
∴多边形的边数由3增加到2021时,其外角和的度数不变,
故选:C.
【点睛】此题考查多边形的外角和,熟记多边形的外角和是360度,并不随边数的变化而变化是解题的关键.
5.7
【分析】多边形的内角和可以表示成(n-2) 180°,外角和都等于360°,故可列方程求解.
【详解】解:设所求多边形边数为n,
则(n-2) 180°=3×360°-180°,
解得n=7.
故答案为:7.
【点睛】本题考查了多边形内角与外角,关键是根据多边形的内角和和外角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
6.6
【详解】设多边形的边数是,
根据题意得,,
解得.
故答案为:6.
7.B
【分析】根据邻补角关系,求得多边形的外角度数,用多边形的外角和定理计算即可.
【详解】解:∵一个正多边形的每个内角都为,
∴这个正多边形的每个外角都为:,
∴这个多边形的边数为:.
故选:B.
【点睛】本题考查了已知多边形的内角求边数,熟练将内角度数转化为外角度数是解题的关键.
8.1440
【分析】由多边形外角的性质可求解多边形的边数,再利用多边形的内角和定理可求解.
【详解】解:,
.
即这个多边形的内角和是,
故答案为:.
【点睛】本题主要考查多边形的内角与外角,求解多边形的边数是解题的关键.
9.C
【分析】设这个正多边形的边数为n,由“如果一个正多边形的一个内角与一个外角的度数之比是7:2”,得出此多边形的外角和为(n-2)×180°,又根据多边形的外角和为360°,由此列出方程,解方程即可.
【详解】解:设这个正多边形的边数为n,
由题意得:(n-2)×180=360,
解得:n=9,
故选:C.
【点睛】此题考查了多边形的内角和与外角和,熟记多边形的内角和公式及多边形的外角和是360°是解题的关键.
10.C
【分析】可先求得的度数,根据四边形内角和为,即可求得答案.
【详解】∵,
∴.
∴.
故选:C.
【点睛】本题主要考查多边形内角和,牢记多边形内角和公式(边形内角和等于)是解题的关键.
11.B
【分析】一个多边形截去一个角(截线不过顶点)之后,则多边形的角增加了一个,求出内角和是2520°的多边形的边数,即可求得原多边形的边数.
【详解】解:设内角和是2520°的多边形的边数是n.
根据题意得:(n-2) 180=2520,
解得:n=16.
则原来的多边形的边数是16-1=15.
故选:B.
【点睛】本题主要考查了多边形的内角和公式,理解新多边形的边数比原多边形的边数增加1是解题的关键.
12.D
【分析】先根据多边形的内角和公式求出截去一个角后的多边形的边数,再根据截去一个角后边数增加1,不变,减少1讨论得解.
【详解】解:设多边形截去一个角的边数为n,
则(n﹣2) 180°=1620°,
解得n=11,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是10或11或12.
故选:D.
【点睛】本题考查了多边形的内角和公式,本题难点在于多边形截去一个角后边数有增加1,不变,减少1三种情况.
13.9或10或11
【分析】先根据多边形的内角和公式求出截去一个角后的多边形的边数,再分情况说明求得原来多边形的解.
【详解】解:设多边形截去一个角的边数为,根据题意得:
又截去一个角后的多边形的边可以增加1、不变、减少1,
原多边形的边数为9或10或11.
【点睛】本题考查的是多边形的内角和公式,本题的易错点在于忽略考虑截去一个角后多边形的边数可以不变、增加或者减少.
14.
【分析】根据题意,小聪走过的路是正多边形,先用除以求出边数,然后再乘以米即可.
【详解】解:∵多边形的边数为,
∴小华要走次才能回到原地,
∴小华走的距离为.
故答案为:.
【点睛】此题考查了多边形的外角和定理,解题的关键是熟记任何一个多边形的外角和都是.
15.B
【分析】根据题意,小明走过的路程是正多边形,先用360°除以45°求出边数,然后再乘以10米即可.
【详解】解:∵小明每次都是沿直线前进10米后再向左转,
∴他走过的图形是正多边形,边数n=360°÷45°=8,
∴小明第一次回到出发点A时所走的路程=8×10=80米.
故选:B.
【点睛】本题考查了正多边形外角问题的实际应用,根据题意判断小明走过的图形是正多边形是解题的关键.
16.D
【分析】因为赛车五次操作后回到出发点,五次操作一种是“正五边形“二种是“五角星“形,根据α最大值小于180°,经过五次操作,绝对不可能三圈或三圈以上.一圈360°或两圈720度.分别用360°和720°除以5,就可以得到答案.
【详解】解:360÷5=72°,
720÷5=144°.
故选D.
【点睛】本题主要考查了正多边形的外角的特点.正多边形的每个外角都相等.
17.120
【详解】解:根据题意,小华所走过的路线是正多边形,
∴边数,
走过的路程最短,则n最小,a最大,
n最小是3,a°最大是120°.
18.C
【分析】根据正五边形和正方形的内角的度数进行计算即可.
【详解】解:如图,∵正五边形的每个内角是,正方形的每个内角,
,
,
故选:C.
【点睛】本题考查了多边形的内角,掌握正五边形和正方形的内角是解题的关键.
19.B
【分析】根据正多边形内角和公式求出正六边形和正五边形的内角和内角的补角,结合三角形内角和定理即可求解;
【详解】解:正六边形的内角为:,内角的补角为:60°;
正五边形的内角为:,内角的补角为:72°;
∴
故选:B
【点睛】本题主要考查多边形内角和公式,三角形的内角和定理,掌握相关知识并正确求解是解题的关键.
20.B
【分析】先根据正多边形的内角和求出,,进而求出 ,再根据四边形的内角和求出答案.
【详解】解:∵六边形为正六边形,
∴.
∵五边形为正五边形,
∴,,
∴.
∵四边形的内角和为,
∴.
故选:B.
【点睛】本题主要考查了多边形的内角和定理,掌握多边形内角和公式是解题的关键.
21.B
【分析】根据正六边形的性质求得、、的度数,根据正五边形的性质求得、的度数,然后再由六边形的内角和求得.
【详解】解:∵六边形,
∴,
∵五边形是正五边形,
∴,
∵,
∴,
故选:B.
【点睛】本题主要考查了正多边形的性质应用,准确计算是解题的关键.
22.B
【分析】根据多边形的内角和公式求得八边形的内角和,然后与多边形的外角和为360°作商即可.
【详解】解:∵八边形的内角和为:,其外角和为,
(倍),
故选:B.
【点睛】本题考查多边形的内角和与外角和,此为基础且重要知识点,必须熟练掌握.
23.B
【分析】设多边形的边数为且为整数),然后利用多边形的内角和公式,结合各项列得方程,解方程求得值,判断值是否符合题意即可.
【详解】解:设多边形的边数为且为整数),
则,
解得:,则A不符合题意;
,
解得:,则B符合题意;
,
解得:,则C不符合题意;
,
解得:,则D不符合题意;
故选:B.
【点睛】本题考查多边形的内角和公式,此为基础且重要知识点,必须熟练掌握.
24.A
【分析】首先根据三角形内角和定理和对顶角得到,然后代入求解即可.
【详解】解:∵,,
∴
∴
,
故选:A.
【点睛】本题主要考查三角形的内角和定理,多边形内角和,对顶角的性质,掌握相关定理是解题的关键.
25.C
【分析】直接利用多边形的内角和公式进行计算即可.
【详解】解:这个八边形的内角和为:;
故选C
【点睛】本题考查的是多边形的内角和定理的应用,熟记多边形内角和公式是解本题的关键.
26.B
【分析】如图,折叠得到,平角的定义,得到,平行线的性质,得到,即可得解.
【详解】解:如图,
∵将纸带沿折叠,点A、D的对应点分别为、,
∴,
∵四边形为一矩形纸带,
∴,
∴,
故选B.
【点睛】本题考查矩形与折叠.解题的关键是掌握矩形的性质,折叠的性质.
27.D
【分析】由题意可知奇奇所走的路线为正多边形,根据多边形的外角和定理即可求出答案.
【详解】解:∵奇奇从A点出发最后回到出发点A时正好走了一个正多边形,
∴根据外角和定理可知正多边形的边数为,
则一共走了米.
故选D.
【点睛】本题主要考查了多边形外角和定理的应用,解题的关键是判断出奇奇所走的路线为正多边形,牢记任何一个多边形的外角和都是,正多边形的每一个外角都相等.
28.C
【分析】由多边形的内角与外角互补求得外角的度数,再由正多边形的外角和为,可得到答案.
【详解】解:∵一个内角的度数是,
∴每个外角度数为,
∴正多边形的边数为:,
即这个多边形是正九边形.
故选C.
【点睛】本题考查正多边形的外角和,熟练掌握正多边形的性质是解题的关键.
29.C
【分析】利用多边形的内角和公式可得五边形的内角和,由平行线的性质可得,从而得到,利用邻补角的定义可得,从而得出,进行计算即可得出的度数.
【详解】解:四边形为五边形,
其内角和为,
,
,
,
,
,
,
,
故选:C.
【点睛】本题主要考查多边形的内角和,平行线的性质,邻补角的定义,熟练掌握多边形的内角和公式,平行线的性质,邻补角的定义,是解题的关键.
30.##360度
【分析】如图所示,与交于点,连接,根据三角形的外角和的性质可得,,由此可将转化为求四边形的内角和,由此即可求解.
【详解】解:如图所示,与交于点,连接,
∴在中,,
在中,,
∴,
∵,,
∴,
∵四边形的内角和为,
∴,
故答案为:.
【点睛】本题主要考查三角形的外角和的性质,四边形的内角和定理,掌握以上知识是解题的关键.
31.##108度
【分析】先根据正多边形内角和公式求出内角的度数,再根据等腰三角形的性质求出,,最后根据三角形内角和定理得出答案.
【详解】解:∵五边形为正五边形,
∴,,
∴,
∴.
故答案为:108°.
【点睛】本题主要考查了多边形内角和定理,三角形内角和定理,掌握多边形内角和计算公式是解题的关键.
32.13
【分析】延长交于点D,与交于点E,根据三角形外角性质和三角形内角和定理计算即可.
【详解】解:延长交于点D,与交于点E,
根据三角形的外角的性质,
,,
∵与的角平分线相交于点P,
∴,
∴,
根据三角形的内角和定理,
,
∴,
∴,
∵,
所以,
故答案为:13.
【点睛】本题考查了角的平分线计算,三角形外角性质,三角形内角和定理,熟练掌握外角性质和角的平分线的意义是解题的关键.
33.##度
【分析】先根据多边形的内角和共求出六边形的内角,然后根据正多边形内角与外角的互补即可求得正六边形和正方形的外角,最后根据三角形的内角和即可求得的度数.
【详解】解:∵图中六边形为正六边形,
∴,
∴,
∵正方形中,,
∴,
∴,
故答案为:.
【点睛】此题考查了正多边形的内角和公式,正多边形的外角与内角的互补,熟记正多边形的内角和公式是解题的关键.
34.(1);(2)十四边形
【分析】(1)分别求出正八边形的每个内角和外角的度数,即可求解;
(2)设这个多边形的边数为,根据题意,列出方程,即可求解.
【详解】解:(1)∵正八边形的每个内角,正八边形的每个外角,
∴;
(2)设这个多边形的边数为,根据题意得:,
解得.
∴这个多边形是十四边形.
【点睛】此题考查多边形内角与外角,正确的列出方程组是解题的关键.
35.(1),证明见解析
(2)
(3)
【分析】(1)根据三角形的内角和定理和对顶角相等即可得出结论;
(2)连接,由(1)可得,则等于五边形内角和;
(3)根据(1)中结论即可求解.
【详解】(1)解:,证明如下:
证明:∵,且,
∴;
故答案为:;
(2)解:连接,
由(1)可得,
∴,
∴五边形内角和,
故答案为:.
(3)解:由(1)中结论可得:,
∵,
∴,
∵平分,平分,
∴,
∴,
由(1)中结论可得:,
故答案为:.
【点睛】本题主要考查了三角形的内角和,多边形的内角和,对顶角相等,解题的关键是掌握三角形的内角和为,多边形内角和为.
36.(1)①见解析 ②见解析
(2)见解析
【分析】(1)①根据多边形内角和可证得,结合,即可得到结论.②根据角平分线的定义可求得,结合,可证得,即可得到结论.
(2)延长,交于点,可先证得,结合,,可求得.
【详解】(1)①∵,,
∴.
∵,
∴.
②∵平分,
∴.
∵平分,
∴.
∴.
∵,
∴.
∴.
∴.
(2)延长,交于点,如图所示:
∵,
∴.
∴.
∵平分,
∴.
∵平分,
∴.
∵,
∴.
∴.
∴.
∴平分.
【点睛】本题主要考查角平分线的定义、三角形的外角的性质、多边形内角和、平行线的判定,能根据题意构建辅助线是解题的关键.
答案第12页,共15页
答案第11页,共15页
