第十二章 第01讲全等三角形的概念与性质 同步学与练(含解析)2023-2024学年八年级数学上册人教版
文档属性
| 名称 | 第十二章 第01讲全等三角形的概念与性质 同步学与练(含解析)2023-2024学年八年级数学上册人教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 00:00:00 | ||
图片预览

文档简介
第01讲 全等三角形的概念与性质
课程标准 学习目标
①全等形的概念 ②全等三角形的概念 ③全等三角形的性质 1. 理解掌握全等形的概念并能够判断全等图形. 2. 理解全等三角形的概念并能够判断全等三角形. 3. 掌握全等三角形的性质,并根据全等三角形的性质熟练解决相关题目.
知识点01 全等形的概念
1. 全等形的概念:
形状和大小完全一样的两个图形叫做全等形.即能够完全重合的两个图形叫做全等形.
题型考点:①概念理解.②全等形判断.
【即学即练1】
1.下列选项中表示两个全等的图形的是( )
A.形状相同的两个图形 B.周长相等的两个图形
C.面积相等的两个图形 D.能够完全重合的两个图形
【即学即练2】
2.下列各项中,两个图形属于全等图形的是( )
A. B.
C. D.
知识点02 全等三角形
1. 全等三角形的概念:
形状和大小完全一样的两个三角形叫做全等三角形.即能够完全重合的两个三角形叫做全等三角形.
2. 全等三角形的相关概念:
如图,若△ABC与△DEF全等.则其中:
能够重合的点叫做全等三角形的对应点.
能够重合的边叫做全等三角形的对应边.
能够重合的角叫做全等三角形的对应角.
用符号“≌”连接,读作全等于.表示△ABC≌△DEF.对应点必须写在对应的位置.
题型考点:①判断全等三角形的对应关系.
【即学即练1】
3.如图,已知,点A与点D,点B与点E,点C与点F是对应顶点.写出这两个三角形的对应边和对应角.
【即学即练2】
4.如图所示,已知,指出它们的对应边和对应角.
知识点03 全等三角形的性质
1. 全等三角形的性质:
由全等三角形的性质及其相关概念可知:
①全等三角形的对应边相等.对应角也相等.
②全等三角形对应边上的中线、高线、角平分线分别对应相等.
③全等的两个三角形它们的周长和面积分别对应相等.
【即学即练1】
5.如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是( )
A.AD=AE B.DB=AE C.DF=EF D.DB=EC
【即学即练2】
6.如图,,,则 .
【即学即练3】
7.如图,,点B、F、C、E在同一条直线上,交于点M,,则的度数是 .
【即学即练4】
8.已知△ABC的三边长分别为3,4,5,△DEF的三边长分别为3,3x﹣2,2x+1,若这两个三角形全等,则x的值为( )
A.2 B.2或 C.或 D.2或或
题型01 利用全等三角形的性质求线段
【典例1】
9.如图,AC⊥BE,DE⊥BE,若△ABC≌△BDE,AC=5,DE=2,则CE等于( )
A.2.5 B.3 C.3.5 D.4
【典例2】
10.如图,,点在同一条直线上,,则的长为( )
A.1 B.2 C.5 D.6
【典例3】
11.如图,,若,则的长为( )
A.6 B.7 C.13 D.19
【典例4】
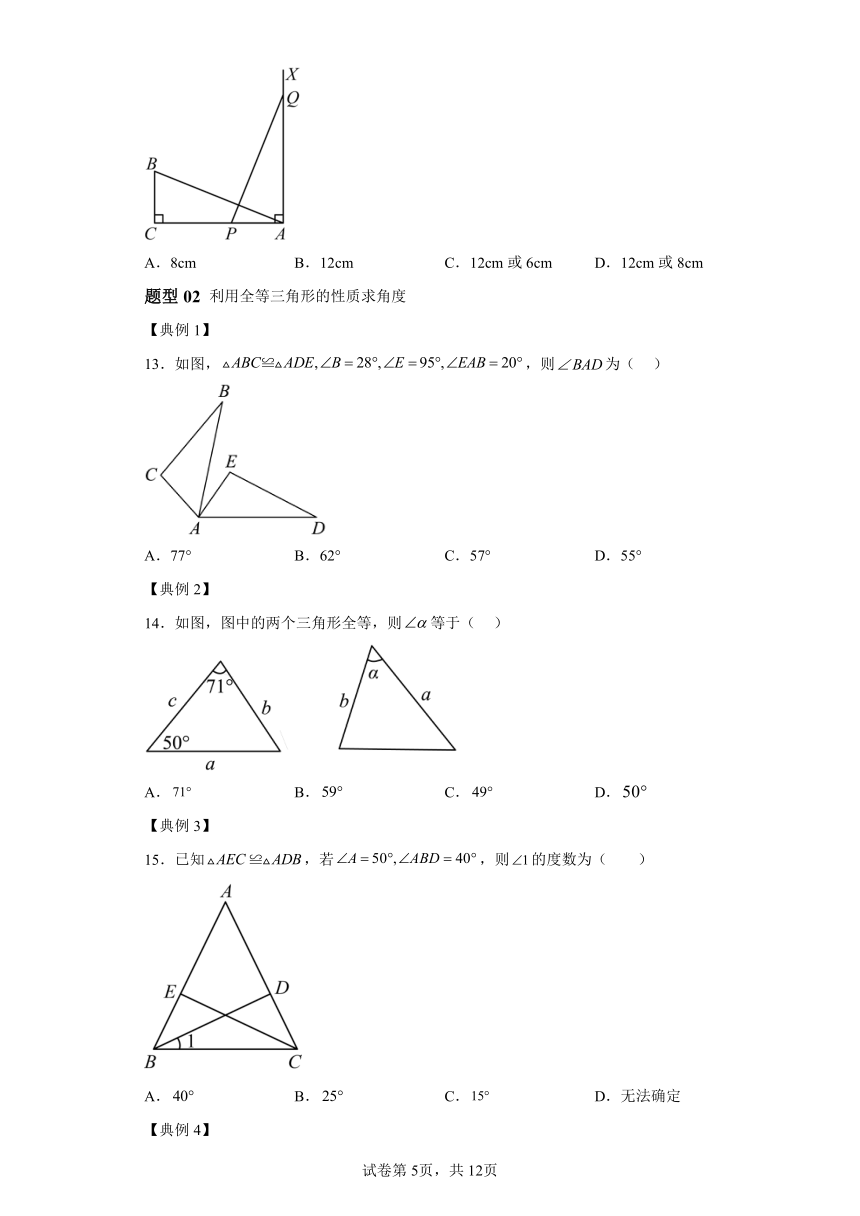
12.如图,在中,,一条线段,P,Q两点分别在线段和的垂线上移动,若以A、B、C为顶点的三角形与以A、P、Q为顶点的三角形全等,则的值为( )
A.8cm B.12cm C.12cm或6cm D.12cm或8cm
题型02 利用全等三角形的性质求角度
【典例1】
13.如图,,则为( )
A.77° B.62° C.57° D.55°
【典例2】
14.如图,图中的两个三角形全等,则等于( )
A. B. C. D.
【典例3】
15.已知,若,则的度数为( )
A. B. C. D.无法确定
【典例4】
16.如图,已知,平分,与交于点G.若,,则的度数是( )
A. B. C. D.
题型03 全等三角形的面积与周长
【典例1】
17.已知△ABC≌△DEF,且△ABC的周长为12 cm,面积为6 cm2,则△DEF的周长为 cm,面积为 cm2.
【典例2】
18.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,,,平移距离为4,则阴影部分面积为( )
A.20 B.24 C.28 D.30
【典例3】
19.如图,若,且,则阴影部分的面积 .
【典例4】
20.如图,在中,于点D,E是上一点,若,,则的周长为( )
A.22 B.23 C.24 D.26
【典例5】
21.如图,,其中,则的周长为 .
【典例6】
22.如图,若,,,,则的周长为 .
题型04 方格中的全等
【典例1】
23.如图,在2×3的正方形方格中,每个正方形方格的边长都为1,则和的关系是( )
A. B. C. D.
【典例2】
24.如图所示的2×2的小正方形方格中,连接AB、AC、AD.则下列结论错误的是( )
A.∠1+∠2=∠3 B.∠1+∠2=2∠3
C.∠1+∠2=90° D.∠1+∠2+∠3=135°
【典例3】
25.如图是由个相同的小正方形组成的网格图,其中等于( )
A. B. C. D.
【典例4】
26.如图,是一个4×4的正方形网格,∠1+∠2+∠3+∠4+∠5+∠6+∠7等于( )
A.585° B.540° C.270° D.315°
27.与下图全等的图形是( )
A. B. C. D.
28.下列说法中,正确的有( )
①形状相同的两个图形是全等形 ②面积相等的两个图形是全等形 ③全等三角形的周长相等,面积相等 ④若,则,
A.1个 B.2个 C.3个 D.4个
29.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90° B.105° C.120° D.135°
30.如图,△ABC≌△EFD,则下列说法错误的是( )
A. B.平行且等于
C.平行且等于 D.
31.如图,在中,在边BC上取一点D,连接AD,在边AD上取一点E,连接CE.若,,则的度数为( )
A. B. C. D.
32.如图,N,C,A三点在同一直线上,N,B,M三点在同一直线上,在中,,又,则的度数等于( )
A.10° B.20° C.30° D.40°
33.如图,△ABC≌△ADE,且AE//BD,∠BAD=96°,则∠BAC的度数的值为( )
A.84° B.60° C.48° D.42°
34.如图,,D在BC上,连接CE,则以下结论:①AD平分∠BDE;②∠CDE=∠BAD;③;④其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
35.如图,,且点B,C,E共线,若的面积为6,,则 .
36.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到的位置,,平移距离为4,则阴影部分的面积为 .
37.如图,点E是CD上的一点,Rt△ACD≌Rt△EBC,则下结论:①AC=BC,②AD∥BE,③∠ACB=90°,④AD+DE=BE,
成立的有 个.
38.如图,于点A,,,射线于点B,一动点E从A点出发以2个单位/秒沿射线运动,点D为射线上一动点,随着E点运动而运动,且始终保持,若点E经过t秒,与全等,则t的值为 秒.
39.如图,已知,点E在边上,与相交于点F.
(1)若,求线段的长;
(2)若,求的度数.
40.如图,,点D在边上,与交于点P,已知,,,.
(1)求的度数.
(2)求与的周长和.
41.如图,已知,点E在上,与相交于点F.
(1)当,时,求线段AE的长;
(2)已知,,求与的度数.
试卷第8页,共12页
试卷第9页,共12页
参考答案:
1.D
【分析】全等图形:能够完全重合的平面图形。特点是形状、大小相同.
【详解】解:A、形状相同的两个图形,大小不一定相同,故此选项错误,不符合题意;
B、周长相等的两个图形,形状、大小不一定相同,故此选项错误,不符合题意;
C、面积相等的两个图形,形状、大小不一定相同,故此选项错误,不符合题意;
D、能够完全重合的两个图形是全等图形,故此选项正确,符合题意;
故选:D.
【点睛】本题考查全等图形的定义.掌握相关结论是解题的关键.
2.C
【分析】利用全等图形的概念:能够完全重合的两个图形叫做全等形可得答案.
【详解】解:A、两个图形不能完全重合,不是全等图形,不符合题意;
B、两个图形不能完全重合,不是全等图形,不符合题意;
C、两个图形能够完全重合,是全等图形,符合题意;
D、两个图形不能完全重合,不是全等图形,不符合题意;
故选:C.
【点睛】本题考查的是全等形的识别、全等图形的基本性质,属于较容易的基础题.
3.见解析
【分析】根据对应顶点,写出对应边和对应角即可.
【详解】解:∵,点A与点D,点B与点E,点C与点F是对应顶点,
∴这两个三角形的对应边是:和,和,和;
对应角是:和,和,和.
【点睛】本题考查全等三角形的性质.正确的找出对应边和对应角,是解题的关键.
4.见解析
【分析】根据全等三角形的概念,正确的确定对应边和对应角即可.
【详解】解:∵,
∴的对应边是,的对应边是,的对应边是,
的对应角是,的对应角是,的对应角是.
【点睛】本题考查全等三角形的概念.熟练掌握全等三角形对应边和对应角的概念,是解题的关键.
5.B
【详解】试题解析:∵△ABE≌△ACD,
∴AB=AC,AD=AE,∠B=∠C,故A正确;
∴AB-AD=AC-AE,即BD=EC,故D正确;
在△BDF和△CEF中
∴△BDF≌△CEF(ASA),
∴DF=EF,故C正确;
故选B.
6.
【分析】根据全等三角形的性质可知解答即可.
【详解】解:∵,
∴,
∵,
∴.
故答案为:10.
【点睛】本题考查了全等三角形的性质,掌握全等三角形的性质是解题的关键.
7.
【分析】先由全等三角形的性质得到,再由三角形外角的性质可得.
【详解】解:∵,
∴,
∴,
故答案为:.
【点睛】本题主要考查了全等三角形的性质,三角形外角的性质,熟知全等三角形对应角相等是解题的关键.
8.A
【分析】首先根据全等三角形的性质:全等三角形的对应边相等可得:3x-2与4是对应边,或3x-2与5是对应边,计算发现,3x-2=5时,2x-1≠4,故3x-2与5不是对应边.
【详解】解:∵△ABC三边长分别为3,4,5,△DEF三边长分别为3,3x-2,2x-1,这两个三角形全等,
①3x-2=4,解得:x=2,
当x=2时,2x+1=5,两个三角形全等.
②当3x-2=5,解得:x=,
把x=代入2x+1≠4,
∴3x-2与5不是对应边,两个三角形不全等.
故选A.
【点睛】此题主要考查了全等三角形的性质,分类讨论正确得出对应边是解题关键.
9.B
【分析】由△ABC≌△BDE,AC=5,DE=2,得到BE=AC=5,BC=DE=2,即可得到答案.
【详解】解:∵△ABC≌△BDE,AC=5,DE=2,
∴BE=AC=5,BC=DE=2,
∴CE=BE-BC=3,
故选:B
【点睛】此题主要考查了全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.
10.A
【分析】由,可得,再由可得,最后计算即可.
【详解】解:∵,
∴,
∵,
∴,
∴,
故选:A.
【点睛】本题考查的是全等三角形的性质,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.
11.B
【分析】根据全等三角形的性质得出,根据,即可求解.
【详解】解:∵,,
∴,
∴,
故选:B.
【点睛】本题考查了全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.
12.C
【分析】分两种情况,由全等三角形对应边相等,即可解决问题.
【详解】解:当时,
∴,
当时,
∴,
∴的值是6cm或12cm.
故选:C.
【点睛】本题考查全等三角形的性质.正确的找到对应边,是解题的关键.注意,分类讨论.
13.A
【分析】根据全等三角形的对应角相等得到,根据三角形内角和定理求出,进而求出.
【详解】解:∵,
∴,
∴,
∴,
故选:A.
【点睛】本题考查全等三角形的性质,三角形的内角和定理.熟练掌握全等三角形的对应角相等,是解题的关键.
14.B
【分析】由全等三角形的对应角相等,结合三角形内角和定理即可得到答案.
【详解】解:由全等三角形的性质可知,两幅图中边长为a、b的夹角对应相等,
∴,
故选:B.
【点睛】本题考查了全等三角形的性质以及三角形内角和定理,解题的关键是掌握全等三角形的对应角相等.
15.B
【分析】由全等三角形的性质可得,由等腰三角形的性质可求的度数,即可求解.
【详解】解:∵,
∴,
∴,
∵,
∴,
∵,
∴,
故选:B.
【点睛】本题考查了全等三角形的性质,等腰三角形的性质,掌握全等三角形的对应边相等是解题的关键.
16.D
【分析】根据角平分线的定义得到,根据全等三角形的性质得到,根据三角形的外角性质、全等三角形的性质解答即可.
【详解】解:∵平分,
∴,
∵,
∴,
又∵,
∴,
∴,
∴,
∵,
∴,故D正确.
故选:D.
【点睛】本题考查的是全等三角形的性质、三角形内角和定理、角平分线的定义,掌握全等三角形的对应角相等是解题的关键.
17. 12 6
【详解】根据全等三角形的性质(两个全等三角形的面积和周长都相等)可得:
因为△ABC≌△DEF,且△ABC的周长为12 cm,面积为6 cm2,
所以△DEF的周长为12cm,面积为6cm2.
故答案是:12,6.
18.A
【分析】根据平移性质得到阴影部分面积等于梯形的面积,然后利用梯形面积公式求解即可.
【详解】解:由平移性质得,,,,
∴,,,
∴
,
故选:A.
【点睛】本题考查平移性质、全等三角形的性质、梯形面积公式,熟练掌握平移性质,得到是解答的关键.
19.16
【分析】根据“全等三角形的对应边相等”推知,然后结合三角形的面积公式作答.
【详解】解:∵,,
∴,
∴.
∴.
故答案为:16.
【点睛】本题考查全等三角形的性质和三角形的面积,熟记知识点是关键.
20.C
【分析】直接利用全等三角形的性质得出,进而得出答案.
【详解】解:∵,
∴,
∵,
∴,
∴的周长为:.
故选:C.
【点睛】本题考查全等三角形的性质,熟练掌握全等三角形的对应边相等,是解题的关键.
21.15
【分析】根据全等三角形的性质求解即可.
【详解】解:∵,,
∴,
∵,
∴的周长,
故答案为:15.
【点睛】本题考查全等三角形的性质.熟练掌握全等三角形的对应边相等,是解题的关键.
22.
【分析】根据全等三角形的性质进行解答即可.
【详解】解:∵,
∴,
∴则的周长,
故答案为:.
【点睛】本题考查了全等三角形的性质,熟知全等三角形对应边相等对应角相等是解本题的关键.
23.C
【分析】先证明,再利用全等三角形的性质和等量代换求解即可.
【详解】解:如图,
在和中,
,
∴,
∴,
∵,
∴,
故选:C.
【点睛】本题考查了全等三角形的判定与性质,利用网格证明三角形全等是解题的关键.
24.A
【分析】根据图形以及勾股定理可以得到边之间关系,从而得到,,为等腰直角三角形,对选项逐个判断即可求解.
【详解】解:如图,,,
∴,,为等腰直角三角形
∴∠4=∠2,∠1=∠5,
A、∠1+∠2=∠1+∠4=90°>∠3,故符合题意
B、∠1+∠2=2∠3=90°,故不符合题意
C、∠1+∠2=∠1+∠4=90°,故不符合题意
D、∠1+∠2+∠3=∠1+∠4+∠3=90°+45°=135°,故不符合题意
故选:A.
【点睛】此题考查了全等三角形的判定与性质,勾股定理,熟练掌握相关基本性质找到角之间的关系是解题的关键.
25.A
【分析】根据可证得,可得出,继而可得出答案.
【详解】解:
由题意得:,
,
,
.
故选:.
【点睛】本题考查全等三角形的性质和判定,解答本题的关键是判断出.
26.A
【分析】根据正方形的轴对称性得∠1+∠7=180°,∠2+∠6=180°,∠3+∠5=180°,∠4=45°.
【详解】解:由图可知,∠1+∠7=180°.
同理得,∠2+∠6=180°,∠3+∠5=180°.
又∠4=45°,
所以∠1+∠2+∠3+∠4+∠5+∠6+∠7=585°.
故选A.
【点睛】本题考查了全等三角形的性质,全等三角形的对应角相等.发现并利用全等三角形是解决本题的关键.
27.B
【分析】根据全等形的定义逐个判定即可得到答案;
【详解】解:由题意可得,
A选项图形与题干图形形状不一样,故不符合题意;
B选项图形与题干图形形状一样,故符合题意;
C选项图形与题干图形形状不一样,故不符合题意;
D选项图形与题干图形形状不一样,故不符合题意;
故选B.
【点睛】本题考查全等形的定义:完全重合的两个图形叫全等形,即形状及大小都相同.
28.A
【分析】根据全等的定义和性质判断即可.
【详解】①形状大小都相同的两个图形是全等形,故①错误;
②面积相等的两个图形不一定是全等形,故②错误;
③全等三角形的周长相等,面积相等,是对的,故③正确;
④若,则,,故④错误;
故正确的有1个.
故选:A
【点睛】此题考查全等三角形的定义和性质,解题关键是掌握全等三角形的定义.
29.D
【分析】根据对称性可得, ,即可求解.
【详解】观察图形可知, 所在的三角形与3所在的三角形全等,
,
又,
.
故选D.
【点睛】主要考查了正方形的性质和全等三角形的判定.充分利用正方形的特殊性质来找到全等的条件从而判定全等后利用全等三角形的性质解题.
30.D
【分析】根据全等三角形对应边相等,对应角相等的性质,然后对各选项分析判断后利用排除法求解.
【详解】解:A、∵△ABC≌△EFD,
∴FD=BC,
∴FD-CD=BC-CD,
即FC=BD,故本选项正确;
B、∵△ABC≌△EFD,
∴EF=AB,∠F=∠B,
∴EF∥AB,故本选项正确;
C、∵△ABC≌△EFD,
∴AC=DE,∠ACB=∠EDF,
∴AC∥DE,故本选项正确;
D、DE是△EFD的边,CD不是△ABC或△EFD的边,且长度不确定,所以CD=ED不成立,故本选项错误.
故选:D.
【点睛】本题主要考查了全等三角形的性质,平行线的性质,熟记性质并对各选项进行准确分析是解题的关键.
31.C
【分析】根据全等三角形对应角相等、三角形外角性质及内角和定理,将△ABC各个角相加,可求出∠ADC=90°,由于全等三角形对应边相等,所以AD=CD,所以∠ACD=45°,则∠ACE=45°-α.
【详解】解:∵
∴∠BAD=∠ECD=α,∠B=∠DEC,∠ADB=∠CDE,AD=CD
∵∠DEC=∠EAC+∠ACE
∴∠BAC+∠B+∠ACB=∠BAD+∠EAC+∠B+∠ECD+∠ACE=∠BAD+2∠B+∠ECD=180°
∴∠B=
∴∠ADC=∠ADB=90°
∵AD=CD
∴∠DAC=∠DCA=45°
∴∠ACE=∠ACD-∠ECD=45°-α
故选 C
【点睛】本题考查了全等三角形的性质、三角形外角性质及内角和定理,根据已知条件熟练运用相关知识是解题的关键.
32.B
【分析】根据三角形的内角和定理求出,根据全等三角形的性质得出,求出,求出的度数即可.
【详解】解:∵在中,,,
∴,
∵,
∴,
∴,
∴,
∴,
故选:B.
【点睛】本题考查全等三角形的性质,三角形的内角和定理.熟练掌握全等三角形的对应角相等,是解题的关键.
33.D
【分析】根据全等三角形的性质得到AB=AD,根据等腰三角形的性质、三角形内角和定理求出∠ADB,根据平行线的性质求出∠DAE,得到答案.
【详解】解:∵△ABC≌△ADE,∠BAD=96°,
∴AB=AD,∠BAC=∠DAE,
∴∠ABD=∠ADB=×(180°﹣96°)=42°,
∵AE//BD,
∴∠DAE=∠ADB=42°,
∴∠BAC=∠DAE=42°.
故选:D.
【点睛】本题主要考查了全等三角形的定制、等腰三角形的性质、三角形的内角和定理以及平行线的性质,灵活运用相关性质定理成为解答本题的关键.
34.C
【分析】由,推出,再由等腰三角形的性质,可以求解.
【详解】解:如图所示:和 交于点O,
,
,
,
平分,
,
,
,
,
由条件不能推出,
正确;
故选:C.
【点睛】本题考查了全等三角形的性质,等腰三角形的性质,关键是掌握并灵活应用全等三角形的对应边相等,对应角相等;等腰三角形的底边相等.
35.1
【分析】设,且,根据得,,则,由的面积为6得进一步得到,即可得到答案.
【详解】解:设,且,
∵,
∴,,
∴,
∵的面积为6,
∴,
∴,
∵,
∴.
故答案为:1
【点睛】此题考查了全等三角形的性质、完全平方公式、算术平方根等知识,数形结合是解题的关键.
36.22
【分析】根据平移的性质分别求出,根据题意求出,根据全等三角形的性质、梯形的面积公式计算,得到答案.
【详解】解:由平移的性质知,,
∴,
根据题意得:,
∴,
∴
,
故答案为:22.
【点睛】本题考查平移及全等三角形的性质,掌握平移的性质是解题的关键.
37.1
【分析】根据全等三角形的性质可以得出AC=BE,CD=BC, ,根据以上结论可以推导出 ,,即可求解.
【详解】解:∵Rt△ACD≌Rt△EBC,
∴AC=BE,
∵在Rt△BEC中,BE<BC,
∴AC<BC,
∴①错误;
∵∠CAD=∠CEB=∠BED=90°,∠D<∠CAD,
∴∠D≠∠BED,
∴AD和BE不平行,
∴②错误;
∵Rt△ACD≌Rt△EBC,
∴∠ACD=∠CBE,∠D=∠BCE,
∵∠CAD=90°,
∴∠ACD+∠D=90°,
∴∠ACB=∠ACD+∠BCE=90°,
∴③正确;
∵Rt△ACD≌Rt△EBC,
∴AD=CE,CD=BC,
CD=CE+DE=AD+DE=BC,
∵BE<BC,
∴AD+DE>BE,
∴④错误;
故答案为:1.
【点睛】本题考查了全等三角形的性质,直角三角形斜边大于直角边等知识,熟练掌握全等三角形的性质是解题关键.
38.2或6或8
【分析】此题要分两种情况:①当E在线段AB上时,②当E在BN上,再分别分成两种情况AC=BE,AB=BE进行计算即可.
【详解】解:①当E在线段AB上,△ACB≌△BED时,AC=BE,
∵AC=4,
∴BE=4,
∴AE=AB-BE=8-4=4,
∴点E的运动时间为t=4÷2=2(秒);
②当E在BN上,AC=BE时,
AE=8+4=12,
点E的运动时间为t=12÷2=6(秒);
③当E在BN上,AB=EB时,△ACB≌△BDE,
AE=8+8=16,
点E的运动时间为t=16÷2=8(秒),
故答案为:2或6或8.
【点睛】本题考查三角形全等的性质,熟练掌握全等三角形的对应边相等是解题的关键.
39.(1)5
(2)
【分析】(1)由,得到,而,即可得到;
(2)由,得到,,由三角形外角的性质得到进行求解即可.
【详解】(1)解:∵,
∴,
∵,
∴;
(2)∵,
∴,,
∵,,
∴.
【点睛】本题考查全等三角形的性质,解题的关键是掌握全等三角形的对应边相等,对应角相等.
40.(1)
(2)
【分析】(1)根据全等三角形的性质得到,计算即可;
(2)根据全等三角形的性质求出、,根据三角形的周长公式计算即可.
【详解】(1)解:∵,,
∴,
∵,
∴,
∴,
即的度数为;
(2)解:∵,
∴,,
∴与的周长和为
.
【点睛】本题主要考查全等三角形的性质,熟练掌握全等三角形的对应角相等,对应边相等是解本题的关键.
41.(1)3
(2),
【分析】(1)根据全等三角形的性质得到,,结合图形计算,即可得到答案;
(2)根据全等三角形的性质得到,,根据三角形内角和定理求出,计算即可求得.
【详解】(1)解:,,,
,,
;
(2)解:,,,
,,,
,
,
,
,
,
.
【点睛】本题考查了全等三角形的性质,三角形的内角和定理,三角形外角的性质,熟练掌握全等三角形的性质是解题的关键.
答案第8页,共18页
答案第7页,共18页
课程标准 学习目标
①全等形的概念 ②全等三角形的概念 ③全等三角形的性质 1. 理解掌握全等形的概念并能够判断全等图形. 2. 理解全等三角形的概念并能够判断全等三角形. 3. 掌握全等三角形的性质,并根据全等三角形的性质熟练解决相关题目.
知识点01 全等形的概念
1. 全等形的概念:
形状和大小完全一样的两个图形叫做全等形.即能够完全重合的两个图形叫做全等形.
题型考点:①概念理解.②全等形判断.
【即学即练1】
1.下列选项中表示两个全等的图形的是( )
A.形状相同的两个图形 B.周长相等的两个图形
C.面积相等的两个图形 D.能够完全重合的两个图形
【即学即练2】
2.下列各项中,两个图形属于全等图形的是( )
A. B.
C. D.
知识点02 全等三角形
1. 全等三角形的概念:
形状和大小完全一样的两个三角形叫做全等三角形.即能够完全重合的两个三角形叫做全等三角形.
2. 全等三角形的相关概念:
如图,若△ABC与△DEF全等.则其中:
能够重合的点叫做全等三角形的对应点.
能够重合的边叫做全等三角形的对应边.
能够重合的角叫做全等三角形的对应角.
用符号“≌”连接,读作全等于.表示△ABC≌△DEF.对应点必须写在对应的位置.
题型考点:①判断全等三角形的对应关系.
【即学即练1】
3.如图,已知,点A与点D,点B与点E,点C与点F是对应顶点.写出这两个三角形的对应边和对应角.
【即学即练2】
4.如图所示,已知,指出它们的对应边和对应角.
知识点03 全等三角形的性质
1. 全等三角形的性质:
由全等三角形的性质及其相关概念可知:
①全等三角形的对应边相等.对应角也相等.
②全等三角形对应边上的中线、高线、角平分线分别对应相等.
③全等的两个三角形它们的周长和面积分别对应相等.
【即学即练1】
5.如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是( )
A.AD=AE B.DB=AE C.DF=EF D.DB=EC
【即学即练2】
6.如图,,,则 .
【即学即练3】
7.如图,,点B、F、C、E在同一条直线上,交于点M,,则的度数是 .
【即学即练4】
8.已知△ABC的三边长分别为3,4,5,△DEF的三边长分别为3,3x﹣2,2x+1,若这两个三角形全等,则x的值为( )
A.2 B.2或 C.或 D.2或或
题型01 利用全等三角形的性质求线段
【典例1】
9.如图,AC⊥BE,DE⊥BE,若△ABC≌△BDE,AC=5,DE=2,则CE等于( )
A.2.5 B.3 C.3.5 D.4
【典例2】
10.如图,,点在同一条直线上,,则的长为( )
A.1 B.2 C.5 D.6
【典例3】
11.如图,,若,则的长为( )
A.6 B.7 C.13 D.19
【典例4】
12.如图,在中,,一条线段,P,Q两点分别在线段和的垂线上移动,若以A、B、C为顶点的三角形与以A、P、Q为顶点的三角形全等,则的值为( )
A.8cm B.12cm C.12cm或6cm D.12cm或8cm
题型02 利用全等三角形的性质求角度
【典例1】
13.如图,,则为( )
A.77° B.62° C.57° D.55°
【典例2】
14.如图,图中的两个三角形全等,则等于( )
A. B. C. D.
【典例3】
15.已知,若,则的度数为( )
A. B. C. D.无法确定
【典例4】
16.如图,已知,平分,与交于点G.若,,则的度数是( )
A. B. C. D.
题型03 全等三角形的面积与周长
【典例1】
17.已知△ABC≌△DEF,且△ABC的周长为12 cm,面积为6 cm2,则△DEF的周长为 cm,面积为 cm2.
【典例2】
18.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,,,平移距离为4,则阴影部分面积为( )
A.20 B.24 C.28 D.30
【典例3】
19.如图,若,且,则阴影部分的面积 .
【典例4】
20.如图,在中,于点D,E是上一点,若,,则的周长为( )
A.22 B.23 C.24 D.26
【典例5】
21.如图,,其中,则的周长为 .
【典例6】
22.如图,若,,,,则的周长为 .
题型04 方格中的全等
【典例1】
23.如图,在2×3的正方形方格中,每个正方形方格的边长都为1,则和的关系是( )
A. B. C. D.
【典例2】
24.如图所示的2×2的小正方形方格中,连接AB、AC、AD.则下列结论错误的是( )
A.∠1+∠2=∠3 B.∠1+∠2=2∠3
C.∠1+∠2=90° D.∠1+∠2+∠3=135°
【典例3】
25.如图是由个相同的小正方形组成的网格图,其中等于( )
A. B. C. D.
【典例4】
26.如图,是一个4×4的正方形网格,∠1+∠2+∠3+∠4+∠5+∠6+∠7等于( )
A.585° B.540° C.270° D.315°
27.与下图全等的图形是( )
A. B. C. D.
28.下列说法中,正确的有( )
①形状相同的两个图形是全等形 ②面积相等的两个图形是全等形 ③全等三角形的周长相等,面积相等 ④若,则,
A.1个 B.2个 C.3个 D.4个
29.如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为( )
A.90° B.105° C.120° D.135°
30.如图,△ABC≌△EFD,则下列说法错误的是( )
A. B.平行且等于
C.平行且等于 D.
31.如图,在中,在边BC上取一点D,连接AD,在边AD上取一点E,连接CE.若,,则的度数为( )
A. B. C. D.
32.如图,N,C,A三点在同一直线上,N,B,M三点在同一直线上,在中,,又,则的度数等于( )
A.10° B.20° C.30° D.40°
33.如图,△ABC≌△ADE,且AE//BD,∠BAD=96°,则∠BAC的度数的值为( )
A.84° B.60° C.48° D.42°
34.如图,,D在BC上,连接CE,则以下结论:①AD平分∠BDE;②∠CDE=∠BAD;③;④其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
35.如图,,且点B,C,E共线,若的面积为6,,则 .
36.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到的位置,,平移距离为4,则阴影部分的面积为 .
37.如图,点E是CD上的一点,Rt△ACD≌Rt△EBC,则下结论:①AC=BC,②AD∥BE,③∠ACB=90°,④AD+DE=BE,
成立的有 个.
38.如图,于点A,,,射线于点B,一动点E从A点出发以2个单位/秒沿射线运动,点D为射线上一动点,随着E点运动而运动,且始终保持,若点E经过t秒,与全等,则t的值为 秒.
39.如图,已知,点E在边上,与相交于点F.
(1)若,求线段的长;
(2)若,求的度数.
40.如图,,点D在边上,与交于点P,已知,,,.
(1)求的度数.
(2)求与的周长和.
41.如图,已知,点E在上,与相交于点F.
(1)当,时,求线段AE的长;
(2)已知,,求与的度数.
试卷第8页,共12页
试卷第9页,共12页
参考答案:
1.D
【分析】全等图形:能够完全重合的平面图形。特点是形状、大小相同.
【详解】解:A、形状相同的两个图形,大小不一定相同,故此选项错误,不符合题意;
B、周长相等的两个图形,形状、大小不一定相同,故此选项错误,不符合题意;
C、面积相等的两个图形,形状、大小不一定相同,故此选项错误,不符合题意;
D、能够完全重合的两个图形是全等图形,故此选项正确,符合题意;
故选:D.
【点睛】本题考查全等图形的定义.掌握相关结论是解题的关键.
2.C
【分析】利用全等图形的概念:能够完全重合的两个图形叫做全等形可得答案.
【详解】解:A、两个图形不能完全重合,不是全等图形,不符合题意;
B、两个图形不能完全重合,不是全等图形,不符合题意;
C、两个图形能够完全重合,是全等图形,符合题意;
D、两个图形不能完全重合,不是全等图形,不符合题意;
故选:C.
【点睛】本题考查的是全等形的识别、全等图形的基本性质,属于较容易的基础题.
3.见解析
【分析】根据对应顶点,写出对应边和对应角即可.
【详解】解:∵,点A与点D,点B与点E,点C与点F是对应顶点,
∴这两个三角形的对应边是:和,和,和;
对应角是:和,和,和.
【点睛】本题考查全等三角形的性质.正确的找出对应边和对应角,是解题的关键.
4.见解析
【分析】根据全等三角形的概念,正确的确定对应边和对应角即可.
【详解】解:∵,
∴的对应边是,的对应边是,的对应边是,
的对应角是,的对应角是,的对应角是.
【点睛】本题考查全等三角形的概念.熟练掌握全等三角形对应边和对应角的概念,是解题的关键.
5.B
【详解】试题解析:∵△ABE≌△ACD,
∴AB=AC,AD=AE,∠B=∠C,故A正确;
∴AB-AD=AC-AE,即BD=EC,故D正确;
在△BDF和△CEF中
∴△BDF≌△CEF(ASA),
∴DF=EF,故C正确;
故选B.
6.
【分析】根据全等三角形的性质可知解答即可.
【详解】解:∵,
∴,
∵,
∴.
故答案为:10.
【点睛】本题考查了全等三角形的性质,掌握全等三角形的性质是解题的关键.
7.
【分析】先由全等三角形的性质得到,再由三角形外角的性质可得.
【详解】解:∵,
∴,
∴,
故答案为:.
【点睛】本题主要考查了全等三角形的性质,三角形外角的性质,熟知全等三角形对应角相等是解题的关键.
8.A
【分析】首先根据全等三角形的性质:全等三角形的对应边相等可得:3x-2与4是对应边,或3x-2与5是对应边,计算发现,3x-2=5时,2x-1≠4,故3x-2与5不是对应边.
【详解】解:∵△ABC三边长分别为3,4,5,△DEF三边长分别为3,3x-2,2x-1,这两个三角形全等,
①3x-2=4,解得:x=2,
当x=2时,2x+1=5,两个三角形全等.
②当3x-2=5,解得:x=,
把x=代入2x+1≠4,
∴3x-2与5不是对应边,两个三角形不全等.
故选A.
【点睛】此题主要考查了全等三角形的性质,分类讨论正确得出对应边是解题关键.
9.B
【分析】由△ABC≌△BDE,AC=5,DE=2,得到BE=AC=5,BC=DE=2,即可得到答案.
【详解】解:∵△ABC≌△BDE,AC=5,DE=2,
∴BE=AC=5,BC=DE=2,
∴CE=BE-BC=3,
故选:B
【点睛】此题主要考查了全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.
10.A
【分析】由,可得,再由可得,最后计算即可.
【详解】解:∵,
∴,
∵,
∴,
∴,
故选:A.
【点睛】本题考查的是全等三角形的性质,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.
11.B
【分析】根据全等三角形的性质得出,根据,即可求解.
【详解】解:∵,,
∴,
∴,
故选:B.
【点睛】本题考查了全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.
12.C
【分析】分两种情况,由全等三角形对应边相等,即可解决问题.
【详解】解:当时,
∴,
当时,
∴,
∴的值是6cm或12cm.
故选:C.
【点睛】本题考查全等三角形的性质.正确的找到对应边,是解题的关键.注意,分类讨论.
13.A
【分析】根据全等三角形的对应角相等得到,根据三角形内角和定理求出,进而求出.
【详解】解:∵,
∴,
∴,
∴,
故选:A.
【点睛】本题考查全等三角形的性质,三角形的内角和定理.熟练掌握全等三角形的对应角相等,是解题的关键.
14.B
【分析】由全等三角形的对应角相等,结合三角形内角和定理即可得到答案.
【详解】解:由全等三角形的性质可知,两幅图中边长为a、b的夹角对应相等,
∴,
故选:B.
【点睛】本题考查了全等三角形的性质以及三角形内角和定理,解题的关键是掌握全等三角形的对应角相等.
15.B
【分析】由全等三角形的性质可得,由等腰三角形的性质可求的度数,即可求解.
【详解】解:∵,
∴,
∴,
∵,
∴,
∵,
∴,
故选:B.
【点睛】本题考查了全等三角形的性质,等腰三角形的性质,掌握全等三角形的对应边相等是解题的关键.
16.D
【分析】根据角平分线的定义得到,根据全等三角形的性质得到,根据三角形的外角性质、全等三角形的性质解答即可.
【详解】解:∵平分,
∴,
∵,
∴,
又∵,
∴,
∴,
∴,
∵,
∴,故D正确.
故选:D.
【点睛】本题考查的是全等三角形的性质、三角形内角和定理、角平分线的定义,掌握全等三角形的对应角相等是解题的关键.
17. 12 6
【详解】根据全等三角形的性质(两个全等三角形的面积和周长都相等)可得:
因为△ABC≌△DEF,且△ABC的周长为12 cm,面积为6 cm2,
所以△DEF的周长为12cm,面积为6cm2.
故答案是:12,6.
18.A
【分析】根据平移性质得到阴影部分面积等于梯形的面积,然后利用梯形面积公式求解即可.
【详解】解:由平移性质得,,,,
∴,,,
∴
,
故选:A.
【点睛】本题考查平移性质、全等三角形的性质、梯形面积公式,熟练掌握平移性质,得到是解答的关键.
19.16
【分析】根据“全等三角形的对应边相等”推知,然后结合三角形的面积公式作答.
【详解】解:∵,,
∴,
∴.
∴.
故答案为:16.
【点睛】本题考查全等三角形的性质和三角形的面积,熟记知识点是关键.
20.C
【分析】直接利用全等三角形的性质得出,进而得出答案.
【详解】解:∵,
∴,
∵,
∴,
∴的周长为:.
故选:C.
【点睛】本题考查全等三角形的性质,熟练掌握全等三角形的对应边相等,是解题的关键.
21.15
【分析】根据全等三角形的性质求解即可.
【详解】解:∵,,
∴,
∵,
∴的周长,
故答案为:15.
【点睛】本题考查全等三角形的性质.熟练掌握全等三角形的对应边相等,是解题的关键.
22.
【分析】根据全等三角形的性质进行解答即可.
【详解】解:∵,
∴,
∴则的周长,
故答案为:.
【点睛】本题考查了全等三角形的性质,熟知全等三角形对应边相等对应角相等是解本题的关键.
23.C
【分析】先证明,再利用全等三角形的性质和等量代换求解即可.
【详解】解:如图,
在和中,
,
∴,
∴,
∵,
∴,
故选:C.
【点睛】本题考查了全等三角形的判定与性质,利用网格证明三角形全等是解题的关键.
24.A
【分析】根据图形以及勾股定理可以得到边之间关系,从而得到,,为等腰直角三角形,对选项逐个判断即可求解.
【详解】解:如图,,,
∴,,为等腰直角三角形
∴∠4=∠2,∠1=∠5,
A、∠1+∠2=∠1+∠4=90°>∠3,故符合题意
B、∠1+∠2=2∠3=90°,故不符合题意
C、∠1+∠2=∠1+∠4=90°,故不符合题意
D、∠1+∠2+∠3=∠1+∠4+∠3=90°+45°=135°,故不符合题意
故选:A.
【点睛】此题考查了全等三角形的判定与性质,勾股定理,熟练掌握相关基本性质找到角之间的关系是解题的关键.
25.A
【分析】根据可证得,可得出,继而可得出答案.
【详解】解:
由题意得:,
,
,
.
故选:.
【点睛】本题考查全等三角形的性质和判定,解答本题的关键是判断出.
26.A
【分析】根据正方形的轴对称性得∠1+∠7=180°,∠2+∠6=180°,∠3+∠5=180°,∠4=45°.
【详解】解:由图可知,∠1+∠7=180°.
同理得,∠2+∠6=180°,∠3+∠5=180°.
又∠4=45°,
所以∠1+∠2+∠3+∠4+∠5+∠6+∠7=585°.
故选A.
【点睛】本题考查了全等三角形的性质,全等三角形的对应角相等.发现并利用全等三角形是解决本题的关键.
27.B
【分析】根据全等形的定义逐个判定即可得到答案;
【详解】解:由题意可得,
A选项图形与题干图形形状不一样,故不符合题意;
B选项图形与题干图形形状一样,故符合题意;
C选项图形与题干图形形状不一样,故不符合题意;
D选项图形与题干图形形状不一样,故不符合题意;
故选B.
【点睛】本题考查全等形的定义:完全重合的两个图形叫全等形,即形状及大小都相同.
28.A
【分析】根据全等的定义和性质判断即可.
【详解】①形状大小都相同的两个图形是全等形,故①错误;
②面积相等的两个图形不一定是全等形,故②错误;
③全等三角形的周长相等,面积相等,是对的,故③正确;
④若,则,,故④错误;
故正确的有1个.
故选:A
【点睛】此题考查全等三角形的定义和性质,解题关键是掌握全等三角形的定义.
29.D
【分析】根据对称性可得, ,即可求解.
【详解】观察图形可知, 所在的三角形与3所在的三角形全等,
,
又,
.
故选D.
【点睛】主要考查了正方形的性质和全等三角形的判定.充分利用正方形的特殊性质来找到全等的条件从而判定全等后利用全等三角形的性质解题.
30.D
【分析】根据全等三角形对应边相等,对应角相等的性质,然后对各选项分析判断后利用排除法求解.
【详解】解:A、∵△ABC≌△EFD,
∴FD=BC,
∴FD-CD=BC-CD,
即FC=BD,故本选项正确;
B、∵△ABC≌△EFD,
∴EF=AB,∠F=∠B,
∴EF∥AB,故本选项正确;
C、∵△ABC≌△EFD,
∴AC=DE,∠ACB=∠EDF,
∴AC∥DE,故本选项正确;
D、DE是△EFD的边,CD不是△ABC或△EFD的边,且长度不确定,所以CD=ED不成立,故本选项错误.
故选:D.
【点睛】本题主要考查了全等三角形的性质,平行线的性质,熟记性质并对各选项进行准确分析是解题的关键.
31.C
【分析】根据全等三角形对应角相等、三角形外角性质及内角和定理,将△ABC各个角相加,可求出∠ADC=90°,由于全等三角形对应边相等,所以AD=CD,所以∠ACD=45°,则∠ACE=45°-α.
【详解】解:∵
∴∠BAD=∠ECD=α,∠B=∠DEC,∠ADB=∠CDE,AD=CD
∵∠DEC=∠EAC+∠ACE
∴∠BAC+∠B+∠ACB=∠BAD+∠EAC+∠B+∠ECD+∠ACE=∠BAD+2∠B+∠ECD=180°
∴∠B=
∴∠ADC=∠ADB=90°
∵AD=CD
∴∠DAC=∠DCA=45°
∴∠ACE=∠ACD-∠ECD=45°-α
故选 C
【点睛】本题考查了全等三角形的性质、三角形外角性质及内角和定理,根据已知条件熟练运用相关知识是解题的关键.
32.B
【分析】根据三角形的内角和定理求出,根据全等三角形的性质得出,求出,求出的度数即可.
【详解】解:∵在中,,,
∴,
∵,
∴,
∴,
∴,
∴,
故选:B.
【点睛】本题考查全等三角形的性质,三角形的内角和定理.熟练掌握全等三角形的对应角相等,是解题的关键.
33.D
【分析】根据全等三角形的性质得到AB=AD,根据等腰三角形的性质、三角形内角和定理求出∠ADB,根据平行线的性质求出∠DAE,得到答案.
【详解】解:∵△ABC≌△ADE,∠BAD=96°,
∴AB=AD,∠BAC=∠DAE,
∴∠ABD=∠ADB=×(180°﹣96°)=42°,
∵AE//BD,
∴∠DAE=∠ADB=42°,
∴∠BAC=∠DAE=42°.
故选:D.
【点睛】本题主要考查了全等三角形的定制、等腰三角形的性质、三角形的内角和定理以及平行线的性质,灵活运用相关性质定理成为解答本题的关键.
34.C
【分析】由,推出,再由等腰三角形的性质,可以求解.
【详解】解:如图所示:和 交于点O,
,
,
,
平分,
,
,
,
,
由条件不能推出,
正确;
故选:C.
【点睛】本题考查了全等三角形的性质,等腰三角形的性质,关键是掌握并灵活应用全等三角形的对应边相等,对应角相等;等腰三角形的底边相等.
35.1
【分析】设,且,根据得,,则,由的面积为6得进一步得到,即可得到答案.
【详解】解:设,且,
∵,
∴,,
∴,
∵的面积为6,
∴,
∴,
∵,
∴.
故答案为:1
【点睛】此题考查了全等三角形的性质、完全平方公式、算术平方根等知识,数形结合是解题的关键.
36.22
【分析】根据平移的性质分别求出,根据题意求出,根据全等三角形的性质、梯形的面积公式计算,得到答案.
【详解】解:由平移的性质知,,
∴,
根据题意得:,
∴,
∴
,
故答案为:22.
【点睛】本题考查平移及全等三角形的性质,掌握平移的性质是解题的关键.
37.1
【分析】根据全等三角形的性质可以得出AC=BE,CD=BC, ,根据以上结论可以推导出 ,,即可求解.
【详解】解:∵Rt△ACD≌Rt△EBC,
∴AC=BE,
∵在Rt△BEC中,BE<BC,
∴AC<BC,
∴①错误;
∵∠CAD=∠CEB=∠BED=90°,∠D<∠CAD,
∴∠D≠∠BED,
∴AD和BE不平行,
∴②错误;
∵Rt△ACD≌Rt△EBC,
∴∠ACD=∠CBE,∠D=∠BCE,
∵∠CAD=90°,
∴∠ACD+∠D=90°,
∴∠ACB=∠ACD+∠BCE=90°,
∴③正确;
∵Rt△ACD≌Rt△EBC,
∴AD=CE,CD=BC,
CD=CE+DE=AD+DE=BC,
∵BE<BC,
∴AD+DE>BE,
∴④错误;
故答案为:1.
【点睛】本题考查了全等三角形的性质,直角三角形斜边大于直角边等知识,熟练掌握全等三角形的性质是解题关键.
38.2或6或8
【分析】此题要分两种情况:①当E在线段AB上时,②当E在BN上,再分别分成两种情况AC=BE,AB=BE进行计算即可.
【详解】解:①当E在线段AB上,△ACB≌△BED时,AC=BE,
∵AC=4,
∴BE=4,
∴AE=AB-BE=8-4=4,
∴点E的运动时间为t=4÷2=2(秒);
②当E在BN上,AC=BE时,
AE=8+4=12,
点E的运动时间为t=12÷2=6(秒);
③当E在BN上,AB=EB时,△ACB≌△BDE,
AE=8+8=16,
点E的运动时间为t=16÷2=8(秒),
故答案为:2或6或8.
【点睛】本题考查三角形全等的性质,熟练掌握全等三角形的对应边相等是解题的关键.
39.(1)5
(2)
【分析】(1)由,得到,而,即可得到;
(2)由,得到,,由三角形外角的性质得到进行求解即可.
【详解】(1)解:∵,
∴,
∵,
∴;
(2)∵,
∴,,
∵,,
∴.
【点睛】本题考查全等三角形的性质,解题的关键是掌握全等三角形的对应边相等,对应角相等.
40.(1)
(2)
【分析】(1)根据全等三角形的性质得到,计算即可;
(2)根据全等三角形的性质求出、,根据三角形的周长公式计算即可.
【详解】(1)解:∵,,
∴,
∵,
∴,
∴,
即的度数为;
(2)解:∵,
∴,,
∴与的周长和为
.
【点睛】本题主要考查全等三角形的性质,熟练掌握全等三角形的对应角相等,对应边相等是解本题的关键.
41.(1)3
(2),
【分析】(1)根据全等三角形的性质得到,,结合图形计算,即可得到答案;
(2)根据全等三角形的性质得到,,根据三角形内角和定理求出,计算即可求得.
【详解】(1)解:,,,
,,
;
(2)解:,,,
,,,
,
,
,
,
,
.
【点睛】本题考查了全等三角形的性质,三角形的内角和定理,三角形外角的性质,熟练掌握全等三角形的性质是解题的关键.
答案第8页,共18页
答案第7页,共18页
