24.3正多边形和圆 课件(共29张PPT)
文档属性
| 名称 | 24.3正多边形和圆 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 18:07:27 | ||
图片预览




文档简介
(共29张PPT)
24.3 正多边形和圆
人教版九年级上册
知识回顾
圆内接四边形的性质:
1.对角 ;
2.四个内角的和是 ;
3.任一外角与其相邻的内角的对角 (即外角等于 ).
互补
360°
相等
内对角
教学目标
1.了解正多边形和圆的有关概念.
2.理解并掌握正多边形半径、中心角、边心距、边长之间的关系.
3.会应用正多边形和圆的有关知识解决实际问题.
新知导入
下面这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗
新知探究
什么叫做正多边形?
各边相等、各角也相等的多边形叫做正多边形.
矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
正多边形
各边相等
各角相等
缺一不可
新知探究
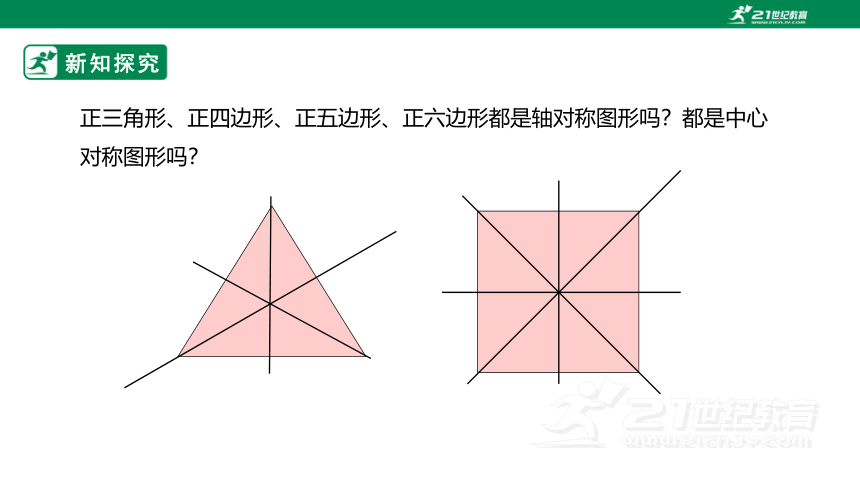
正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
新知探究
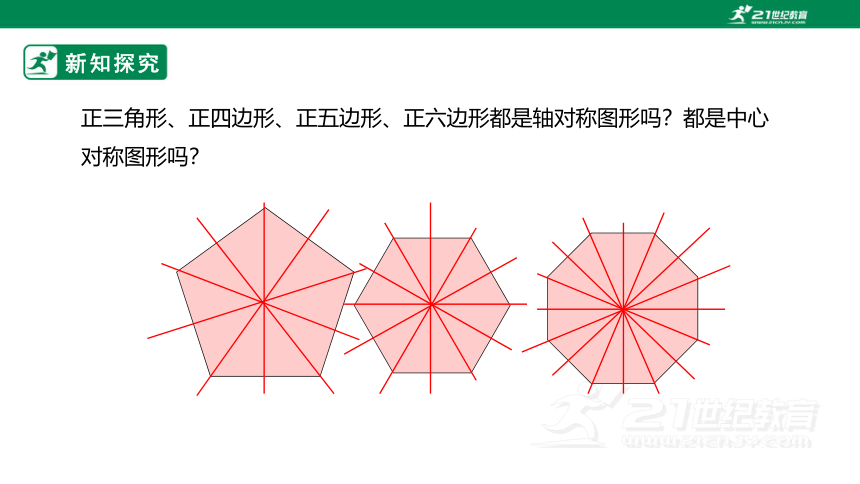
正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
新知探究
O
A
B
C
D
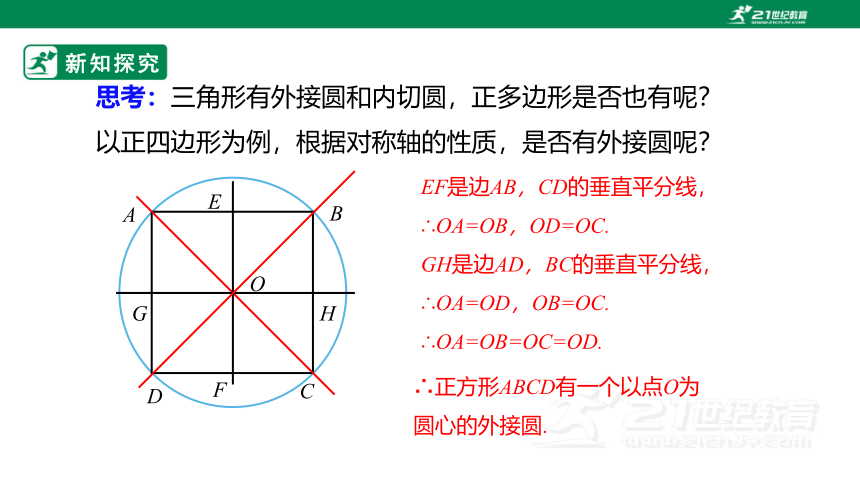
思考:三角形有外接圆和内切圆,正多边形是否也有呢?
以正四边形为例,根据对称轴的性质,是否有外接圆呢?
E
F
G
H
EF是边AB,CD的垂直平分线,∴OA=OB,OD=OC.
GH是边AD,BC的垂直平分线,
∴OA=OD,OB=OC.
∴OA=OB=OC=OD.
∴正方形ABCD有一个以点O为圆心的外接圆.
新知探究
O
A
B
C
D
E
F
G
H
AC平分∠DAB及∠DCB,BD平分∠ABC及∠ADC,
∴OE=OH=OF=OG.
∴正方形ABCD还有一个以点O为圆心的内切圆.
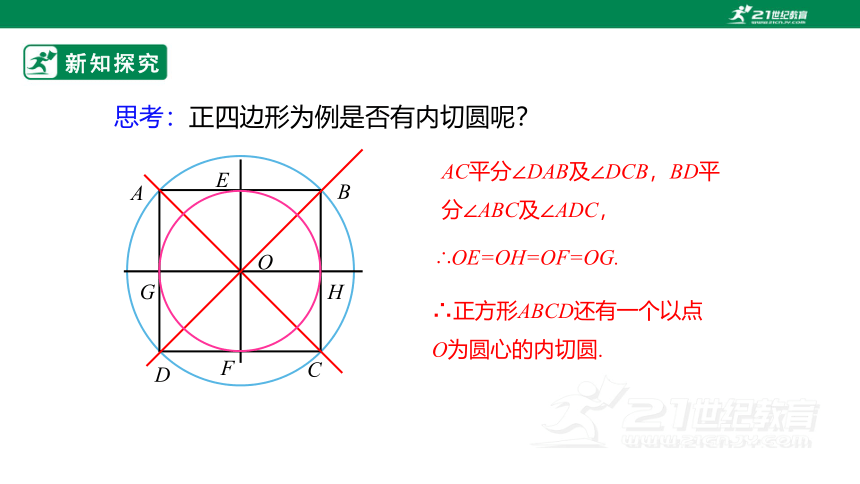
思考:正四边形为例是否有内切圆呢?
新知探究
思考:所有的正多边形是不是都有一个外接圆和一个内切圆?
任何正多边形都有一个外接圆和一个内切圆.
思考:能否借助圆画正n边形呢?
(1)如果将圆n等分,依次连接各分点得到一个n边形,这个n边形一定是正n边形吗?
新知探究
如图,在⊙O中,A,B,C,D,E是⊙O的五等分点.依次连接ABCDE形成五边形.
例1
解:五边形ABCDE是正五边形.证明如下:
在⊙O中,
∴AB=BC=CD=DE=EA,
∴∠A=∠B;
同理∠B=∠C=∠D=∠E.
又∵五边形ABCDE的顶点都在⊙O上,
问:五边形ABCDE是正五边形吗?如果是,请证明你的结论.
∴五边形ABCDE是正五边形.
问:各边相等的圆内接多边形是正多边形吗?各角相等的圆内接多边形是正多边形吗?
新知练习
1.如图所示,△AOB是正三角形,以点O为圆心,OA为半径作☉O,直径FC//AB,AO,BO的延长线分别交☉O于点D,E.求证:六边形ABCDEF为圆内接正六边形.
解: ∵ △AOB是正三角形,
∴ ∠AOB=∠OAB=∠OBA =60° ,OB=OA,∴点B在☉O上.
∵FC//AB,∴ ∠FOA= ∠OAB =60°,∠COB=∠OBA= 60°,
∴ ∠AOB=∠BOC=∠COD= ∠DOE=∠EOF=∠FOA=60°.
∴ .
∴六边形ABCDEF为圆内接正六边形.
新知小结
1、任意三角形都有外接圆和内切圆,但是只有正三角形的外接圆和内切圆是同心圆;
2、任意多边形不一定有外接圆和内切圆,但当多边形是正多边形时,一定有一个外接圆和一个内切圆,并且这两个圆是同心圆.
新知小结
把圆分成n(n≥3)等份,依次连接各分点得到的多边形就是这个圆的内接正n边形,这个圆就是这个正n边形的外接圆.
圆内接正多边形
圆的外切正n边形
把圆分成n(n≥3)等份,经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.一定要注意正多边形的半径是指外接圆的半径,而不是内切圆的半径.
新知探究
1.一个正多边形的各个顶点都在一个圆上,则这个正多边形就是这个圆的 ,圆叫做这个多边形的 .
2.一个正多边形的外接圆的______叫做正多边形的中心.
3.外接圆的______叫做正多边形的半径.
4.正多边形每一边所对的 叫做正多边形的中心角.
5.中心到正多边形的一边的 叫做正多边形的边心距
半径R
边心距r
中心角
内接多边形
外接圆
圆心
半径
圆心角
距离
新知探究
已知正六边形的半径为R,求正六边形的边长、边心距和面积.
例2
解:如图,∵正六边形的中心角为60°,
∴∠AOB=60°.
∵OA=OB,
∴AB=OA=R.
过点O作OM⊥AB于点M,
则AM=
在Rt△OAM中,OM=
∴S正六边形=6S△OBA=6× AB·OM=
M
o
A
B
∴△OBA是等边三角形.
新知练习
2.有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积 (结果保留小数点后一位).
抽象成
新知练习
利用勾股定理,可得边心距 r ==2
亭子地基的面积
在Rt△OPB中,OB=4 m, PB= = =2(m),
过点O作OP⊥BC于P.
解:如图,连接OB, OC.因为六边形ABCDEF是正六边形,所以它的中心角等于=60°,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此亭子地基的周长 l=6×4=24(m),
新知小结
正n边形的中心角怎么计算?
正n边形的边长a,半径R,边心距r之间有什么关系?
边长为a,边心距为r的正n边形的面积如何计算?
其中l为正n边形的周长.
新知小结
正多边形的有关结论
1.正六边形的边长等于其外接圆的半径;正三角形的边长等于其外接圆半径的倍;正方形的边长等于其外接圆半径的倍.
2.若已知正n边形的边长、周长、边心距、面积中的任意一项,则可求出其他各项.
3.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形,所以在进行与正多边形有关的计算时,可以把正多边形的计算转化到直角三角形中,利用勾股定理等知识解决.
4.由正多边形的内角与外角互补,正多边形的中心角等于外角,可得正多边形的中心角和内角互补.
新知小结
2.作边心距,构造直角三角形.
1.连半径,得中心角;
O
A
B
C
D
E
F
R
M
r
·
圆内接正多边形的辅助线
O
边心距r
边长一半
半径R
B
M
中心角一半
课堂总结
正多边形的性质
正多边形的
有关概念
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
中心
半径
边心距
中心角
正多边形的对称性
课堂练习
1.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A
A.正三角形 B.正方形
C.正五边形 D.正六边形
解:∵正三角形一条边所对的圆心角是360°÷3=120°,
正方形一条边所对的圆心角是360°÷4=90°,
正五边形一条边所对的圆心角是360°÷5=72°,
正六边形一条边所对的圆心角是360°÷6=60°,
∴一条边所对的圆心角最大的图形是正三角形.
课堂练习
2.正三角形的边心距、半径和高的比为( )
A.1∶2∶ B.1: :3
C.1∶ ∶ D.1∶2:3
3.如图,正六边形的内切圆的半径OD= cm,则它的中心角∠AOB=____,边长AB=____cm,正六边形的面积S= cm2.
D
60°
2
课堂练习
解:(1) 正多边形必有外接圆,作出正五边形的外接圆☉O,如图,
则所对的圆心角的度数均为,
∵∠EAC的度数等于所对的圆心角的度数的一半,
∴∠EAC= .
同理∠AED= .
∴∠EAC+∠AED=180°,∴AC//ED.
4.如图,正五边形ABCDE的对角线AC和BE相交于点M.
求证:(1) AC//ED;(2) ME=AE.
课堂练习
5.已知边长为4的等边三角形ABC,求△ABC的中心角、半径、边心距、面积.
解:如图所示,过点A作AD⊥BC于点D,过点B作BE⊥AC于点E,
AD,BE交于点O,连接CO.
由题意得BD=CD=2,AE=EC=2,
AD垂直平分BC,BE垂直平分AC,
∴AO=CO,CO=BO,∴AO=CO=BO,
∴点O为等边三角形ABC的中心.
∵ ∠BOC=2∠BAC,∠BAC= 60°, ∴ △ABC的中心角∠BOC = 120°.
∵OB=OC, ∴ ∠OBC=∠OCB=.
课堂练习
设OD=x,则OB =2x.
在Rt△BOD中,根据勾股定理得(2x)2-x2 =22,∴x=,
∴等边三角形ABC的边心距为,半径为.
∴ S△ABC= BC·AD= ×4×(+ )=4.
5.已知边长为4的等边三角形ABC,求△ABC的中心角、半径、边心距、面积.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.3 正多边形和圆
人教版九年级上册
知识回顾
圆内接四边形的性质:
1.对角 ;
2.四个内角的和是 ;
3.任一外角与其相邻的内角的对角 (即外角等于 ).
互补
360°
相等
内对角
教学目标
1.了解正多边形和圆的有关概念.
2.理解并掌握正多边形半径、中心角、边心距、边长之间的关系.
3.会应用正多边形和圆的有关知识解决实际问题.
新知导入
下面这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗
新知探究
什么叫做正多边形?
各边相等、各角也相等的多边形叫做正多边形.
矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
正多边形
各边相等
各角相等
缺一不可
新知探究
正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
新知探究
正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
新知探究
O
A
B
C
D
思考:三角形有外接圆和内切圆,正多边形是否也有呢?
以正四边形为例,根据对称轴的性质,是否有外接圆呢?
E
F
G
H
EF是边AB,CD的垂直平分线,∴OA=OB,OD=OC.
GH是边AD,BC的垂直平分线,
∴OA=OD,OB=OC.
∴OA=OB=OC=OD.
∴正方形ABCD有一个以点O为圆心的外接圆.
新知探究
O
A
B
C
D
E
F
G
H
AC平分∠DAB及∠DCB,BD平分∠ABC及∠ADC,
∴OE=OH=OF=OG.
∴正方形ABCD还有一个以点O为圆心的内切圆.
思考:正四边形为例是否有内切圆呢?
新知探究
思考:所有的正多边形是不是都有一个外接圆和一个内切圆?
任何正多边形都有一个外接圆和一个内切圆.
思考:能否借助圆画正n边形呢?
(1)如果将圆n等分,依次连接各分点得到一个n边形,这个n边形一定是正n边形吗?
新知探究
如图,在⊙O中,A,B,C,D,E是⊙O的五等分点.依次连接ABCDE形成五边形.
例1
解:五边形ABCDE是正五边形.证明如下:
在⊙O中,
∴AB=BC=CD=DE=EA,
∴∠A=∠B;
同理∠B=∠C=∠D=∠E.
又∵五边形ABCDE的顶点都在⊙O上,
问:五边形ABCDE是正五边形吗?如果是,请证明你的结论.
∴五边形ABCDE是正五边形.
问:各边相等的圆内接多边形是正多边形吗?各角相等的圆内接多边形是正多边形吗?
新知练习
1.如图所示,△AOB是正三角形,以点O为圆心,OA为半径作☉O,直径FC//AB,AO,BO的延长线分别交☉O于点D,E.求证:六边形ABCDEF为圆内接正六边形.
解: ∵ △AOB是正三角形,
∴ ∠AOB=∠OAB=∠OBA =60° ,OB=OA,∴点B在☉O上.
∵FC//AB,∴ ∠FOA= ∠OAB =60°,∠COB=∠OBA= 60°,
∴ ∠AOB=∠BOC=∠COD= ∠DOE=∠EOF=∠FOA=60°.
∴ .
∴六边形ABCDEF为圆内接正六边形.
新知小结
1、任意三角形都有外接圆和内切圆,但是只有正三角形的外接圆和内切圆是同心圆;
2、任意多边形不一定有外接圆和内切圆,但当多边形是正多边形时,一定有一个外接圆和一个内切圆,并且这两个圆是同心圆.
新知小结
把圆分成n(n≥3)等份,依次连接各分点得到的多边形就是这个圆的内接正n边形,这个圆就是这个正n边形的外接圆.
圆内接正多边形
圆的外切正n边形
把圆分成n(n≥3)等份,经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.一定要注意正多边形的半径是指外接圆的半径,而不是内切圆的半径.
新知探究
1.一个正多边形的各个顶点都在一个圆上,则这个正多边形就是这个圆的 ,圆叫做这个多边形的 .
2.一个正多边形的外接圆的______叫做正多边形的中心.
3.外接圆的______叫做正多边形的半径.
4.正多边形每一边所对的 叫做正多边形的中心角.
5.中心到正多边形的一边的 叫做正多边形的边心距
半径R
边心距r
中心角
内接多边形
外接圆
圆心
半径
圆心角
距离
新知探究
已知正六边形的半径为R,求正六边形的边长、边心距和面积.
例2
解:如图,∵正六边形的中心角为60°,
∴∠AOB=60°.
∵OA=OB,
∴AB=OA=R.
过点O作OM⊥AB于点M,
则AM=
在Rt△OAM中,OM=
∴S正六边形=6S△OBA=6× AB·OM=
M
o
A
B
∴△OBA是等边三角形.
新知练习
2.有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积 (结果保留小数点后一位).
抽象成
新知练习
利用勾股定理,可得边心距 r ==2
亭子地基的面积
在Rt△OPB中,OB=4 m, PB= = =2(m),
过点O作OP⊥BC于P.
解:如图,连接OB, OC.因为六边形ABCDEF是正六边形,所以它的中心角等于=60°,△OBC是等边三角形,从而正六边形的边长等于它的半径.
因此亭子地基的周长 l=6×4=24(m),
新知小结
正n边形的中心角怎么计算?
正n边形的边长a,半径R,边心距r之间有什么关系?
边长为a,边心距为r的正n边形的面积如何计算?
其中l为正n边形的周长.
新知小结
正多边形的有关结论
1.正六边形的边长等于其外接圆的半径;正三角形的边长等于其外接圆半径的倍;正方形的边长等于其外接圆半径的倍.
2.若已知正n边形的边长、周长、边心距、面积中的任意一项,则可求出其他各项.
3.正n边形的半径和边心距把正n边形分成2n个全等的直角三角形,所以在进行与正多边形有关的计算时,可以把正多边形的计算转化到直角三角形中,利用勾股定理等知识解决.
4.由正多边形的内角与外角互补,正多边形的中心角等于外角,可得正多边形的中心角和内角互补.
新知小结
2.作边心距,构造直角三角形.
1.连半径,得中心角;
O
A
B
C
D
E
F
R
M
r
·
圆内接正多边形的辅助线
O
边心距r
边长一半
半径R
B
M
中心角一半
课堂总结
正多边形的性质
正多边形的
有关概念
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
中心
半径
边心距
中心角
正多边形的对称性
课堂练习
1.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )
A
A.正三角形 B.正方形
C.正五边形 D.正六边形
解:∵正三角形一条边所对的圆心角是360°÷3=120°,
正方形一条边所对的圆心角是360°÷4=90°,
正五边形一条边所对的圆心角是360°÷5=72°,
正六边形一条边所对的圆心角是360°÷6=60°,
∴一条边所对的圆心角最大的图形是正三角形.
课堂练习
2.正三角形的边心距、半径和高的比为( )
A.1∶2∶ B.1: :3
C.1∶ ∶ D.1∶2:3
3.如图,正六边形的内切圆的半径OD= cm,则它的中心角∠AOB=____,边长AB=____cm,正六边形的面积S= cm2.
D
60°
2
课堂练习
解:(1) 正多边形必有外接圆,作出正五边形的外接圆☉O,如图,
则所对的圆心角的度数均为,
∵∠EAC的度数等于所对的圆心角的度数的一半,
∴∠EAC= .
同理∠AED= .
∴∠EAC+∠AED=180°,∴AC//ED.
4.如图,正五边形ABCDE的对角线AC和BE相交于点M.
求证:(1) AC//ED;(2) ME=AE.
课堂练习
5.已知边长为4的等边三角形ABC,求△ABC的中心角、半径、边心距、面积.
解:如图所示,过点A作AD⊥BC于点D,过点B作BE⊥AC于点E,
AD,BE交于点O,连接CO.
由题意得BD=CD=2,AE=EC=2,
AD垂直平分BC,BE垂直平分AC,
∴AO=CO,CO=BO,∴AO=CO=BO,
∴点O为等边三角形ABC的中心.
∵ ∠BOC=2∠BAC,∠BAC= 60°, ∴ △ABC的中心角∠BOC = 120°.
∵OB=OC, ∴ ∠OBC=∠OCB=.
课堂练习
设OD=x,则OB =2x.
在Rt△BOD中,根据勾股定理得(2x)2-x2 =22,∴x=,
∴等边三角形ABC的边心距为,半径为.
∴ S△ABC= BC·AD= ×4×(+ )=4.
5.已知边长为4的等边三角形ABC,求△ABC的中心角、半径、边心距、面积.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
