27.1 图形的相似一课一练(含解析)
文档属性
| 名称 | 27.1 图形的相似一课一练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 409.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 22:50:06 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
27.1 图形的相似一课一练
一、填空题
1.把一个矩形剪去一个正方形,若余下的矩形与原矩形相似,则原矩形长宽之比为 .
二、单选题
2.下列图形中一定是相似形的是( )
A.两个菱形 B.两个等边三角形
C.两个矩形 D.两个直角三角形
3.下列叙述正确的是( )
A.任意两个等腰三角形相似 B.任意两个平行四边形相似
C.任意两个矩形相似 D.任意两个正方形相似
4.在我们日常生活中存在很多较小的或眼睛不易辨清的物体,利用放大镜“放大”,可以使人看得更清楚.如图,利用放大镜可以看清辣椒表面的纹路,这种图形的变换是( )
A.平移变换 B.旋转变换 C.轴对称变换 D.相似变换
5.如图的两个四边形相似,则∠a的度数是( )
A.120° B.87° C.75° D.60°
6.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为( )
A.70° B.80° C.90° D.120°
7.下列各组图形中,两个图形形状不一定相同的是( )
A.两个等边三角形
B.有一个角是35°的两个等腰三角形
C.两个正方形
D.两个圆
三、解答题
8.如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
四、作图题
9.如图所示,请你画一画,试着把下面两个图形用给出的格点缩小为原来的 .
五、综合题
10.方格图中的每个小方格都是边长为1小正方形,我们把小正方形的顶点称为格点,格点连线为边的四边形称为“格点四边形”,图1中的四边形ABCD就是一个格点四边形.
(1)小彬在图2的方格图中画了一个格点四边形EFGH.借助方格图回答:四边形ABCD与四边形EFGH相似吗?若相似,直接写出四边形ABCD与四边形EFGH的相似比;若不相似说明理由;
(2)请在图3的方格图中画一个格点四边形,使它与四边形ABCD相似,但与四边形ABCD、四边形EFGH都不全等.
11.如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长.
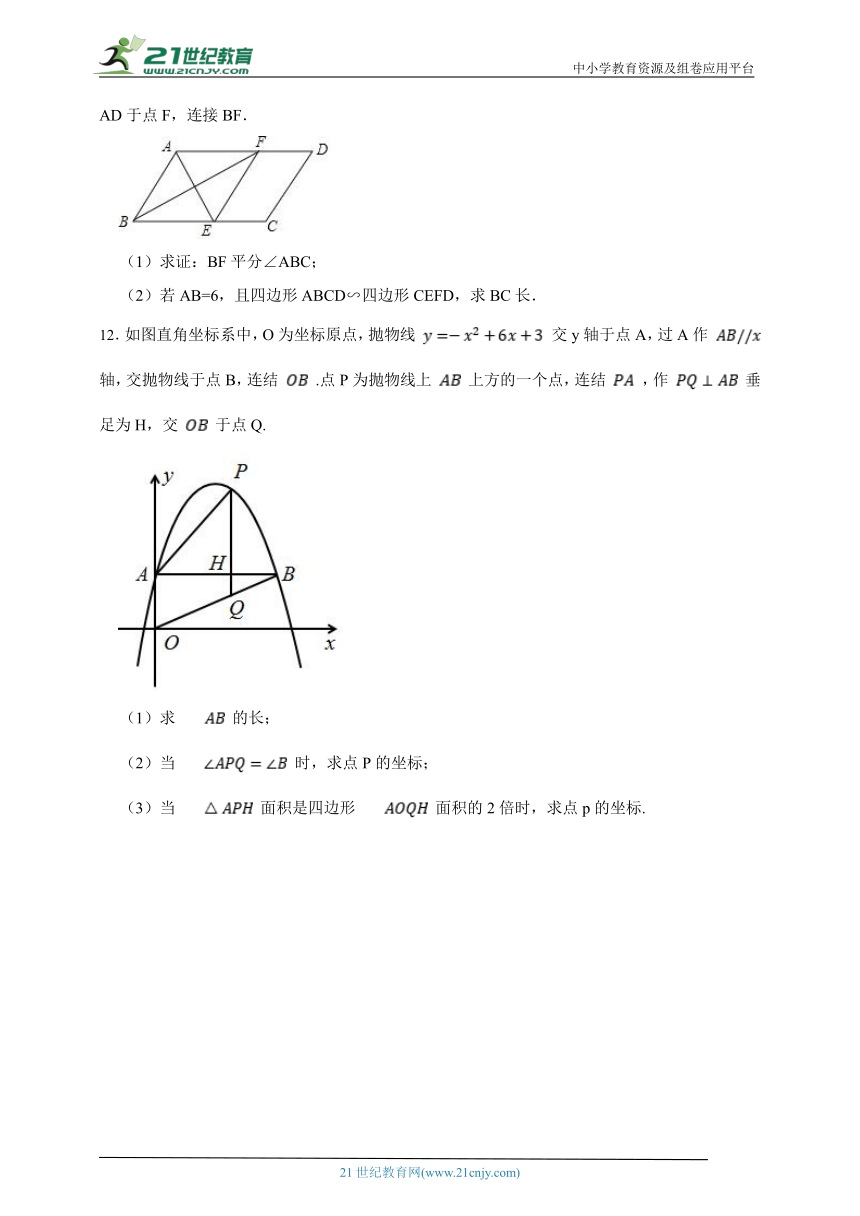
12.如图直角坐标系中,O为坐标原点,抛物线 交y轴于点A,过A作 轴,交抛物线于点B,连结 .点P为抛物线上 上方的一个点,连结 ,作 垂足为H,交 于点Q.
(1)求 的长;
(2)当 时,求点P的坐标;
(3)当 面积是四边形 面积的2倍时,求点p的坐标.
答案解析部分
1.【答案】
【解析】【解答】
根据相似多边形对应边的成比例,=,
设原矩形ABCD的长AD=x,宽AB=y,则AE=x-y.
∴=
解得:x=,或x=(舍去).
∴=.
即原矩形的长与宽的比是.
【分析】根据相似多边形对应边的比等于相似比,设出原来矩形的长和宽,就可得到关于长宽的方程,从而可以解得.
2.【答案】B
【解析】【解答】解:∵等边三角形的对应角相等,对应边的比相等,
∴两个等边三角形一定是相似形,
又∵直角三角形,菱形的对应角不一定相等,矩形的边不一定对应成比例,
∴两个直角三角形、两个菱形、两个矩形都不一定是相似形,
故答案为:B.
【分析】 对应角相等,对应边的比相等的两个图形就叫相似图形。根据相似图形的定义对每个选项一一判断即可。
3.【答案】D
【解析】【解答】解: A、任意两个等腰三角形不一定满足三边对应成比例,三个角分别对应相等,不一定相似,故此选项不符合题意;
B、任意两个平行四边形不一定满足边对应成比例,四个角对应相等,不一定相似,故此选项不符合题意;
C、任意两个矩形不一定满足边对应成比例,不一定相似,故此选项不符合题意;
D、任意两个两个正方形满足相似图形的定义,故选项符合题意.
故答案为:D.
【分析】对应边成比例,且对应角相等的两个图形相似,据此一一判断得出答案.
4.【答案】D
【解析】【解答】解:利用放大镜可以看清辣椒表面的纹路,这种图形的变换是相似变换.
故答案为:D.
【分析】根据相似图形的概念即可得出答案。
5.【答案】B
【解析】【解答】解:如图,
∵两个四边形相似,
∴ ,
∵四边形的内角和等于360°,
∴ .
故答案为:B.
【分析】利用相似四边形的对应角相等,可求出∠1的度数,再利用四边形的内角和定理可求出∠a的度数.
6.【答案】B
【解析】【解答】解:∵四边形ABCD∽四边形EFGH,∠A=80°,
∴∠E=∠A=80°,
故答案为:B
【分析】根据相似多边形的对应角相等可求解.
7.【答案】B
【解析】【解答】解:A、相似,因为其三个角均相等,符合相似三角形的判定;
B、不相似,因为没有指明该角是顶角还是底角,若一个顶角和一个底角相等则不一定相似;
C、相似,因为其四个角均相等,且对应边成比例,符合相似的条件;
D、相似,因为圆是以定点为圆心,定长为半径所组成的图形,符合相似的条件;
故答案为:B
【分析】根据相似图形的性质判断。
8.【答案】解:设运动了ts,根据题意得:AP=2tcm,CQ=3tcm,则AQ=AC﹣CQ=16﹣3t(cm),当△APQ∽△ABC时, ,即 ,解得:t= ;当△APQ∽△ACB时, ,即 ,解得:t=4;故当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是: s或4s.
【解析】【分析】由题意根据路程=速度时间,可将AP、CQ、AQ用含t的代数式表示。因为∠A时公共角,所以以A、P、Q为顶点的三角形与△ABC相似时分两种情况讨论求解:
①当△APQ∽△ABC时,可得比例式,代入可得关于t的方程,解方程即可求解;
②当△APQ∽△ACB时,可得比例式,代入可得关于t的方程,解方程即可求解。
9.【答案】解:如图所示:
【解析】【分析】将图形中对应边长变为原来的 得出对应点位置画出图形即可.
10.【答案】(1)解:相似;
根据题意,四边形ABCD中, ,BC=1,CD=2,AD= ;四边形EFGH中, ,FG=2,GH=4,EH= ;
∴ ,即 ,
∴四边形ABCD与四边形EFGH相似,相似比为: .
(2)解:根据题意,设相似比为 ,则四边形MNPQ的各边为:
MN=2,NP= ,PQ= ,MQ= ,
如图,四边形MNPQ即为所求.
.
【解析】【分析】(1)分别求出四边形各边的长度,求出对应边的相似比,即可得到答案;(2)先确定相似比,然后求出个对应边的长度,即可画出图形.
11.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD,∴∠FAE=∠AEB,∵EF∥AB,
∴四边形ABEF是平行四边形,
∵AE平分∠BAD,∴∠FAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=EB,
∴四边形ABEF是菱形,
∴BF平分∠ABC
(2)解:∵四边形ABEF为菱形;
∴BE=AB=6,
∵四边形ABCD∽四边形CEFD,
∴ ,即 ,
解得:BC=3±3 (负值舍去),
∴BC=3+3
【解析】【分析】(1)利用平行四边形的性质,可证得AD∥BC,AB=CD,利用两组对边分别平行的四边形是平行四边形,可证得四边形ABEF是平行四边形,再根据角平分线的定义及平行线的性质,去证明AB=EB,就可证得四边形ABEF是菱形,然后根据菱形的性质可证得结论。
(2)利用相似多边形的性质和菱形的性质,由四边形ABCD∽四边形CEFD,得出对应边成比例,就可求出BC的长。
12.【答案】(1)解:当x=0时,y=3,
∴A(0,3),
令 ,解得x=0或6,
∴B(6,3),
故AB=6;
(2)解:设P(m,-m2+6m+3),
∵∠P=∠B,∠AHP=∠OAB=90°,
∴△ABO∽△HPA,
∴,
∴,
解得m=4,
∴P(4,11);
(3)解:当 面积是四边形 面积的2倍时, 则2(3+)=-m2+6m,
解得m1=4, m2=3,
∴P(4,11)或(3,12).
【解析】【分析】 (1)对于y=-x2+6x+3,令x=0,则y=3,故点A(0,3),令y=-x2+6x+3=3,解得x=0或6,故点B(6,3),即可求解;
(2)根据题意,证明△ABO~△HPA,则,据此列式即可求解;
(3)当△APH的面积是四边形AOQH的面积的2倍时,则2(AO+HQ)=PH,即可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
27.1 图形的相似一课一练
一、填空题
1.把一个矩形剪去一个正方形,若余下的矩形与原矩形相似,则原矩形长宽之比为 .
二、单选题
2.下列图形中一定是相似形的是( )
A.两个菱形 B.两个等边三角形
C.两个矩形 D.两个直角三角形
3.下列叙述正确的是( )
A.任意两个等腰三角形相似 B.任意两个平行四边形相似
C.任意两个矩形相似 D.任意两个正方形相似
4.在我们日常生活中存在很多较小的或眼睛不易辨清的物体,利用放大镜“放大”,可以使人看得更清楚.如图,利用放大镜可以看清辣椒表面的纹路,这种图形的变换是( )
A.平移变换 B.旋转变换 C.轴对称变换 D.相似变换
5.如图的两个四边形相似,则∠a的度数是( )
A.120° B.87° C.75° D.60°
6.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为( )
A.70° B.80° C.90° D.120°
7.下列各组图形中,两个图形形状不一定相同的是( )
A.两个等边三角形
B.有一个角是35°的两个等腰三角形
C.两个正方形
D.两个圆
三、解答题
8.如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?
四、作图题
9.如图所示,请你画一画,试着把下面两个图形用给出的格点缩小为原来的 .
五、综合题
10.方格图中的每个小方格都是边长为1小正方形,我们把小正方形的顶点称为格点,格点连线为边的四边形称为“格点四边形”,图1中的四边形ABCD就是一个格点四边形.
(1)小彬在图2的方格图中画了一个格点四边形EFGH.借助方格图回答:四边形ABCD与四边形EFGH相似吗?若相似,直接写出四边形ABCD与四边形EFGH的相似比;若不相似说明理由;
(2)请在图3的方格图中画一个格点四边形,使它与四边形ABCD相似,但与四边形ABCD、四边形EFGH都不全等.
11.如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长.
12.如图直角坐标系中,O为坐标原点,抛物线 交y轴于点A,过A作 轴,交抛物线于点B,连结 .点P为抛物线上 上方的一个点,连结 ,作 垂足为H,交 于点Q.
(1)求 的长;
(2)当 时,求点P的坐标;
(3)当 面积是四边形 面积的2倍时,求点p的坐标.
答案解析部分
1.【答案】
【解析】【解答】
根据相似多边形对应边的成比例,=,
设原矩形ABCD的长AD=x,宽AB=y,则AE=x-y.
∴=
解得:x=,或x=(舍去).
∴=.
即原矩形的长与宽的比是.
【分析】根据相似多边形对应边的比等于相似比,设出原来矩形的长和宽,就可得到关于长宽的方程,从而可以解得.
2.【答案】B
【解析】【解答】解:∵等边三角形的对应角相等,对应边的比相等,
∴两个等边三角形一定是相似形,
又∵直角三角形,菱形的对应角不一定相等,矩形的边不一定对应成比例,
∴两个直角三角形、两个菱形、两个矩形都不一定是相似形,
故答案为:B.
【分析】 对应角相等,对应边的比相等的两个图形就叫相似图形。根据相似图形的定义对每个选项一一判断即可。
3.【答案】D
【解析】【解答】解: A、任意两个等腰三角形不一定满足三边对应成比例,三个角分别对应相等,不一定相似,故此选项不符合题意;
B、任意两个平行四边形不一定满足边对应成比例,四个角对应相等,不一定相似,故此选项不符合题意;
C、任意两个矩形不一定满足边对应成比例,不一定相似,故此选项不符合题意;
D、任意两个两个正方形满足相似图形的定义,故选项符合题意.
故答案为:D.
【分析】对应边成比例,且对应角相等的两个图形相似,据此一一判断得出答案.
4.【答案】D
【解析】【解答】解:利用放大镜可以看清辣椒表面的纹路,这种图形的变换是相似变换.
故答案为:D.
【分析】根据相似图形的概念即可得出答案。
5.【答案】B
【解析】【解答】解:如图,
∵两个四边形相似,
∴ ,
∵四边形的内角和等于360°,
∴ .
故答案为:B.
【分析】利用相似四边形的对应角相等,可求出∠1的度数,再利用四边形的内角和定理可求出∠a的度数.
6.【答案】B
【解析】【解答】解:∵四边形ABCD∽四边形EFGH,∠A=80°,
∴∠E=∠A=80°,
故答案为:B
【分析】根据相似多边形的对应角相等可求解.
7.【答案】B
【解析】【解答】解:A、相似,因为其三个角均相等,符合相似三角形的判定;
B、不相似,因为没有指明该角是顶角还是底角,若一个顶角和一个底角相等则不一定相似;
C、相似,因为其四个角均相等,且对应边成比例,符合相似的条件;
D、相似,因为圆是以定点为圆心,定长为半径所组成的图形,符合相似的条件;
故答案为:B
【分析】根据相似图形的性质判断。
8.【答案】解:设运动了ts,根据题意得:AP=2tcm,CQ=3tcm,则AQ=AC﹣CQ=16﹣3t(cm),当△APQ∽△ABC时, ,即 ,解得:t= ;当△APQ∽△ACB时, ,即 ,解得:t=4;故当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是: s或4s.
【解析】【分析】由题意根据路程=速度时间,可将AP、CQ、AQ用含t的代数式表示。因为∠A时公共角,所以以A、P、Q为顶点的三角形与△ABC相似时分两种情况讨论求解:
①当△APQ∽△ABC时,可得比例式,代入可得关于t的方程,解方程即可求解;
②当△APQ∽△ACB时,可得比例式,代入可得关于t的方程,解方程即可求解。
9.【答案】解:如图所示:
【解析】【分析】将图形中对应边长变为原来的 得出对应点位置画出图形即可.
10.【答案】(1)解:相似;
根据题意,四边形ABCD中, ,BC=1,CD=2,AD= ;四边形EFGH中, ,FG=2,GH=4,EH= ;
∴ ,即 ,
∴四边形ABCD与四边形EFGH相似,相似比为: .
(2)解:根据题意,设相似比为 ,则四边形MNPQ的各边为:
MN=2,NP= ,PQ= ,MQ= ,
如图,四边形MNPQ即为所求.
.
【解析】【分析】(1)分别求出四边形各边的长度,求出对应边的相似比,即可得到答案;(2)先确定相似比,然后求出个对应边的长度,即可画出图形.
11.【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD,∴∠FAE=∠AEB,∵EF∥AB,
∴四边形ABEF是平行四边形,
∵AE平分∠BAD,∴∠FAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=EB,
∴四边形ABEF是菱形,
∴BF平分∠ABC
(2)解:∵四边形ABEF为菱形;
∴BE=AB=6,
∵四边形ABCD∽四边形CEFD,
∴ ,即 ,
解得:BC=3±3 (负值舍去),
∴BC=3+3
【解析】【分析】(1)利用平行四边形的性质,可证得AD∥BC,AB=CD,利用两组对边分别平行的四边形是平行四边形,可证得四边形ABEF是平行四边形,再根据角平分线的定义及平行线的性质,去证明AB=EB,就可证得四边形ABEF是菱形,然后根据菱形的性质可证得结论。
(2)利用相似多边形的性质和菱形的性质,由四边形ABCD∽四边形CEFD,得出对应边成比例,就可求出BC的长。
12.【答案】(1)解:当x=0时,y=3,
∴A(0,3),
令 ,解得x=0或6,
∴B(6,3),
故AB=6;
(2)解:设P(m,-m2+6m+3),
∵∠P=∠B,∠AHP=∠OAB=90°,
∴△ABO∽△HPA,
∴,
∴,
解得m=4,
∴P(4,11);
(3)解:当 面积是四边形 面积的2倍时, 则2(3+)=-m2+6m,
解得m1=4, m2=3,
∴P(4,11)或(3,12).
【解析】【分析】 (1)对于y=-x2+6x+3,令x=0,则y=3,故点A(0,3),令y=-x2+6x+3=3,解得x=0或6,故点B(6,3),即可求解;
(2)根据题意,证明△ABO~△HPA,则,据此列式即可求解;
(3)当△APH的面积是四边形AOQH的面积的2倍时,则2(AO+HQ)=PH,即可求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
