27.2.1 相似三角形的判定一课一练(含解析)
文档属性
| 名称 | 27.2.1 相似三角形的判定一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 418.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
27.2.1 相似三角形的判定一课一练
一、填空题
1.如图,△ABC是等腰三角形,AB=AC=8,BC=3,点D在AB边上,点E在CB的延长线上,已知AD=3,BE=2,连接ED并延长交AC于点F,则线段AF的长为 .
二、单选题
2.下列四组线段中,不能成比例的是( )
A.a=3,b=6,c=2,d=4 B.a=1,b=3,c=2,d=6
C.a=4,b=6,c=5,d=10 D.a=2,b=5,c=4,d=10
3.如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
A.∠ABD=∠C B.∠ADB=∠ABC C. D.
4.把ad=bc写成比例式,错误的是 ( )
A. B. C. D.
5.如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若AD:DB=3:2,则AE:AC等于( )
A.3:2 B.3:1 C.2:3 D.3:5
6.某同学的身高为1.6米,某一时刻他在阳光下的影长为1.2米,与他相邻的一棵树的影长为3.6米,则这棵树的高度为( ).
A.5. 3米 B.4.8米 C.4.0米 D.2.7米
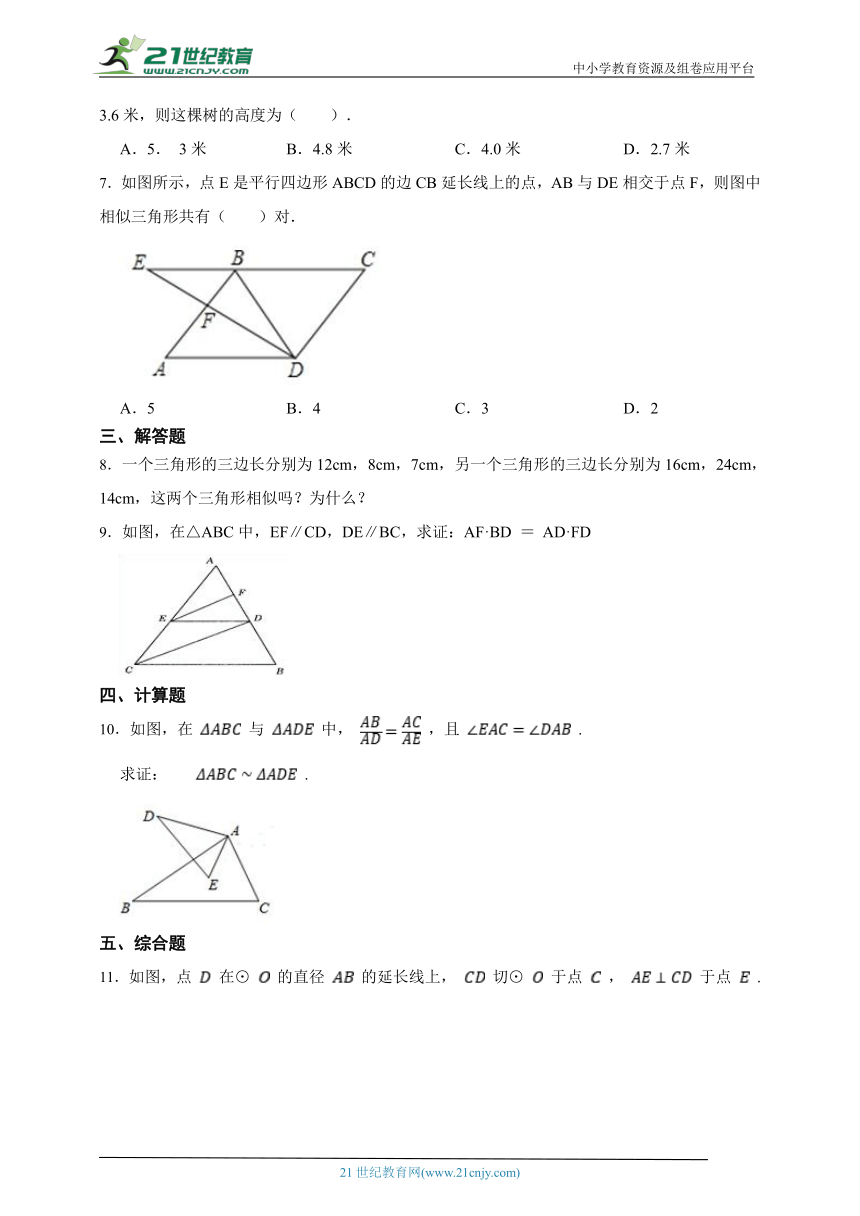
7.如图所示,点E是平行四边形ABCD的边CB延长线上的点,AB与DE相交于点F,则图中相似三角形共有( )对.
A.5 B.4 C.3 D.2
三、解答题
8.一个三角形的三边长分别为12cm,8cm,7cm,另一个三角形的三边长分别为16cm,24cm,14cm,这两个三角形相似吗?为什么?
9.如图,在△ABC中,EF∥CD,DE∥BC,求证:AF·BD = AD·FD
四、计算题
10.如图,在 与 中, ,且 .
求证: .
五、综合题
11.如图,点 在⊙ 的直径 的延长线上, 切⊙ 于点 , 于点 .
(1)求证: 平分 ;
(2)若 , ,求 的长.
12.如图,在坐标平面上,O为原点,另有A(0,3),B(﹣5,0),C(6,0)三点,直线L通过C点且与y轴相交于D点,请回答下列问题:
(1)已知直线L的方程为5x﹣3y=k,求k的值.
(2)承(1),请完整说明△AOB与△COD相似的理由.
答案解析部分
1.【答案】
【解析】【解答】解:过 点作 ,交 于点 ,如图所示:
∵BG∥EF,即 ,
∴ ,
∴AF= AG,
∴ ,
∵BC=3,BE=2,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴AC=AF+FG+CG= ,
∴FG= ,
∴ ;
故答案为: .
【分析】先求出,再求出,最后计算求解即可。
2.【答案】C
【解析】【解答】解:A、∵2×6=3×4,∴四组线段中能成比例;不符合题意;
B、∵1×6=3×2,∴四组线段中能成比例;不符合题意;
C、∵4×10≠5×6,∴四组线段中不能成比例;符合题意;
D、∵2×10=4×10,∴四组线段中能成比例;不符合题意;
故答案为:C.
【分析】根据比例的性质验证四条线段是否两两乘积相等即可判断求解.
3.【答案】C
【解析】【解答】解:∵∠A是公共角,
∴当∠ABD=∠C或∠ADB=∠ABC时,△ADB∽△ABC(有两角对应相等的三角形相似);
故A与B正确;
当 时,△ADB∽△ABC(两组对应边的比相等且夹角对应相等的两个三角形相似);
故D正确;
当 时,∠A不是夹角,故不能判定△ADB与△ABC相似,
故C错误.
故答案为:C.
【分析】△ADB与△ABC中已经有一个公共角相等,要使△ADB与△ABC相似,可以添加∠ABD=∠C或∠ADB=∠ABC或=即可,从而作出判断。
4.【答案】D
【解析】∵ad=bc,
∴写成比例式为:a:b=c:d、b:d=a:c、b:a=d:c,
故题中D选项是错误的,故选D.
5.【答案】D
【解析】【解答】∵DE∥BC,根据平行线分线段成比例定理,AD:DB=3:2,
∴AE:EC=3:2,∴AE:AC=3:5.
故答案为:D.
【分析】根据平行线分线段成比例,分析判断即可。
6.【答案】B
【解析】【解答】根据同一时刻物体的高度和物体的影长成比例可得:1.6:1.2=树高:3.6,则可解得树高为4.8m.
故答案为:B
【分析】根据同一时刻,同一地点,同一平面内,不同物体的高度与该物体的影长成比例,即可列出方程,求解即可。
7.【答案】B
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴AB∥CD,BC∥AD,△ADB∽△CBD,
∵BF∥CD,
∴△EFB∽△EDC,
∵BE∥AD,
∴△EFB∽△DFA,
∴△EDC∽△DFA.
故选B.
【分析】根据平行四边形的性质得AB∥CD,BC∥AD,△ADB∽△CBD,再利用平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似,由BF∥CD得到△EFB∽△EDC,由BE∥AD得到△EFB∽△DFA,根据相似的传递性得到△EDC∽△DFA.
8.【答案】解:∵ , , ,
∴这两个三角形相似
【解析】【分析】根据相似三角形的判定定理:三边对应成比例,两个三角形相似,可知这两个三角形相似。
9.【答案】证明:∵EF∥CD,∴AF:DF=AE:EC, ∵DE∥BC,∴AD:DE=AE:EC.
∴AF:DF=AD:DB, ∴AF·BD = AD·FD .
【解析】【分析】由题意知EF∥CD,DE∥BC,根据平行线分线段成比例定理可得比例式:AF:DF=AE:EC,AD:DE=AE:EC;于是可得AF:DF=AD:DB,将比例式化为乘积式即可求解。
10.【答案】证明:∵ ,
∴ ,
即 ,
又 ,
∴ .
【解析】【分析】先证得 ,利用有两条对应边的比相等,且其夹角相等,即可判定两个三角形相似.
11.【答案】(1)证明:连接OC,则OC⊥CD,∵AE⊥CD,∴OC∥AE,∴∠CAE=∠ACO,
∵OA=OC,∴∠OAC=∠ACO,
∴∠EAC=∠OAC,∴AC平分∠DAE。
(2)解:∵AB=6,∴OA=OB=3,Rt△OCD中,OC=OB=3,OD=3+2=5,由勾股定理得CD=4.
∵OC∥AE,∴ ,即 ,解得CE= .
【解析】【分析】(1)因为CD切⊙ O 于点 C , 所以连接OC,则OC⊥CD,由AE⊥CD,及OA=OC,即可证明∠EAC=∠OAC;
(2)Rt△OCD中,由勾股定理得CD=;由OC∥AE,可得,代入相关数据计算即可。
12.【答案】(1)解:∵直线L:5x﹣3y=k过点C(6,0),
∴5×6﹣3×0=k,
∴k=30,
(2)解:由(1)知,直线L:5x﹣3y=30,
∵直线L与y轴的交点为D,
令x=0,
∴﹣3y=30,
∴y=﹣10,
∴D(0,﹣10),
∴OD=10,
∵A(0,3),B(﹣5,0),C(6,0),
∴OA=3,OB=5,OC=6,
∴ = , = ,
∴ ,
∵∠AOB=∠COD=90°,
∴△AOB∽△COD.
【解析】【分析】(1)利用函数图象上的的特点,即可求出k的值.
(2)根据坐标分别求出OA,OB,OC,OD,即可得出,即可得出结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
27.2.1 相似三角形的判定一课一练
一、填空题
1.如图,△ABC是等腰三角形,AB=AC=8,BC=3,点D在AB边上,点E在CB的延长线上,已知AD=3,BE=2,连接ED并延长交AC于点F,则线段AF的长为 .
二、单选题
2.下列四组线段中,不能成比例的是( )
A.a=3,b=6,c=2,d=4 B.a=1,b=3,c=2,d=6
C.a=4,b=6,c=5,d=10 D.a=2,b=5,c=4,d=10
3.如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )
A.∠ABD=∠C B.∠ADB=∠ABC C. D.
4.把ad=bc写成比例式,错误的是 ( )
A. B. C. D.
5.如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若AD:DB=3:2,则AE:AC等于( )
A.3:2 B.3:1 C.2:3 D.3:5
6.某同学的身高为1.6米,某一时刻他在阳光下的影长为1.2米,与他相邻的一棵树的影长为3.6米,则这棵树的高度为( ).
A.5. 3米 B.4.8米 C.4.0米 D.2.7米
7.如图所示,点E是平行四边形ABCD的边CB延长线上的点,AB与DE相交于点F,则图中相似三角形共有( )对.
A.5 B.4 C.3 D.2
三、解答题
8.一个三角形的三边长分别为12cm,8cm,7cm,另一个三角形的三边长分别为16cm,24cm,14cm,这两个三角形相似吗?为什么?
9.如图,在△ABC中,EF∥CD,DE∥BC,求证:AF·BD = AD·FD
四、计算题
10.如图,在 与 中, ,且 .
求证: .
五、综合题
11.如图,点 在⊙ 的直径 的延长线上, 切⊙ 于点 , 于点 .
(1)求证: 平分 ;
(2)若 , ,求 的长.
12.如图,在坐标平面上,O为原点,另有A(0,3),B(﹣5,0),C(6,0)三点,直线L通过C点且与y轴相交于D点,请回答下列问题:
(1)已知直线L的方程为5x﹣3y=k,求k的值.
(2)承(1),请完整说明△AOB与△COD相似的理由.
答案解析部分
1.【答案】
【解析】【解答】解:过 点作 ,交 于点 ,如图所示:
∵BG∥EF,即 ,
∴ ,
∴AF= AG,
∴ ,
∵BC=3,BE=2,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴AC=AF+FG+CG= ,
∴FG= ,
∴ ;
故答案为: .
【分析】先求出,再求出,最后计算求解即可。
2.【答案】C
【解析】【解答】解:A、∵2×6=3×4,∴四组线段中能成比例;不符合题意;
B、∵1×6=3×2,∴四组线段中能成比例;不符合题意;
C、∵4×10≠5×6,∴四组线段中不能成比例;符合题意;
D、∵2×10=4×10,∴四组线段中能成比例;不符合题意;
故答案为:C.
【分析】根据比例的性质验证四条线段是否两两乘积相等即可判断求解.
3.【答案】C
【解析】【解答】解:∵∠A是公共角,
∴当∠ABD=∠C或∠ADB=∠ABC时,△ADB∽△ABC(有两角对应相等的三角形相似);
故A与B正确;
当 时,△ADB∽△ABC(两组对应边的比相等且夹角对应相等的两个三角形相似);
故D正确;
当 时,∠A不是夹角,故不能判定△ADB与△ABC相似,
故C错误.
故答案为:C.
【分析】△ADB与△ABC中已经有一个公共角相等,要使△ADB与△ABC相似,可以添加∠ABD=∠C或∠ADB=∠ABC或=即可,从而作出判断。
4.【答案】D
【解析】∵ad=bc,
∴写成比例式为:a:b=c:d、b:d=a:c、b:a=d:c,
故题中D选项是错误的,故选D.
5.【答案】D
【解析】【解答】∵DE∥BC,根据平行线分线段成比例定理,AD:DB=3:2,
∴AE:EC=3:2,∴AE:AC=3:5.
故答案为:D.
【分析】根据平行线分线段成比例,分析判断即可。
6.【答案】B
【解析】【解答】根据同一时刻物体的高度和物体的影长成比例可得:1.6:1.2=树高:3.6,则可解得树高为4.8m.
故答案为:B
【分析】根据同一时刻,同一地点,同一平面内,不同物体的高度与该物体的影长成比例,即可列出方程,求解即可。
7.【答案】B
【解析】【解答】解:∵四边形ABCD为平行四边形,
∴AB∥CD,BC∥AD,△ADB∽△CBD,
∵BF∥CD,
∴△EFB∽△EDC,
∵BE∥AD,
∴△EFB∽△DFA,
∴△EDC∽△DFA.
故选B.
【分析】根据平行四边形的性质得AB∥CD,BC∥AD,△ADB∽△CBD,再利用平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似,由BF∥CD得到△EFB∽△EDC,由BE∥AD得到△EFB∽△DFA,根据相似的传递性得到△EDC∽△DFA.
8.【答案】解:∵ , , ,
∴这两个三角形相似
【解析】【分析】根据相似三角形的判定定理:三边对应成比例,两个三角形相似,可知这两个三角形相似。
9.【答案】证明:∵EF∥CD,∴AF:DF=AE:EC, ∵DE∥BC,∴AD:DE=AE:EC.
∴AF:DF=AD:DB, ∴AF·BD = AD·FD .
【解析】【分析】由题意知EF∥CD,DE∥BC,根据平行线分线段成比例定理可得比例式:AF:DF=AE:EC,AD:DE=AE:EC;于是可得AF:DF=AD:DB,将比例式化为乘积式即可求解。
10.【答案】证明:∵ ,
∴ ,
即 ,
又 ,
∴ .
【解析】【分析】先证得 ,利用有两条对应边的比相等,且其夹角相等,即可判定两个三角形相似.
11.【答案】(1)证明:连接OC,则OC⊥CD,∵AE⊥CD,∴OC∥AE,∴∠CAE=∠ACO,
∵OA=OC,∴∠OAC=∠ACO,
∴∠EAC=∠OAC,∴AC平分∠DAE。
(2)解:∵AB=6,∴OA=OB=3,Rt△OCD中,OC=OB=3,OD=3+2=5,由勾股定理得CD=4.
∵OC∥AE,∴ ,即 ,解得CE= .
【解析】【分析】(1)因为CD切⊙ O 于点 C , 所以连接OC,则OC⊥CD,由AE⊥CD,及OA=OC,即可证明∠EAC=∠OAC;
(2)Rt△OCD中,由勾股定理得CD=;由OC∥AE,可得,代入相关数据计算即可。
12.【答案】(1)解:∵直线L:5x﹣3y=k过点C(6,0),
∴5×6﹣3×0=k,
∴k=30,
(2)解:由(1)知,直线L:5x﹣3y=30,
∵直线L与y轴的交点为D,
令x=0,
∴﹣3y=30,
∴y=﹣10,
∴D(0,﹣10),
∴OD=10,
∵A(0,3),B(﹣5,0),C(6,0),
∴OA=3,OB=5,OC=6,
∴ = , = ,
∴ ,
∵∠AOB=∠COD=90°,
∴△AOB∽△COD.
【解析】【分析】(1)利用函数图象上的的特点,即可求出k的值.
(2)根据坐标分别求出OA,OB,OC,OD,即可得出,即可得出结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
