【金版学案】2014-2015学年高中数学章末知识整合(人教版必修三)第二章
文档属性
| 名称 | 【金版学案】2014-2015学年高中数学章末知识整合(人教版必修三)第二章 | 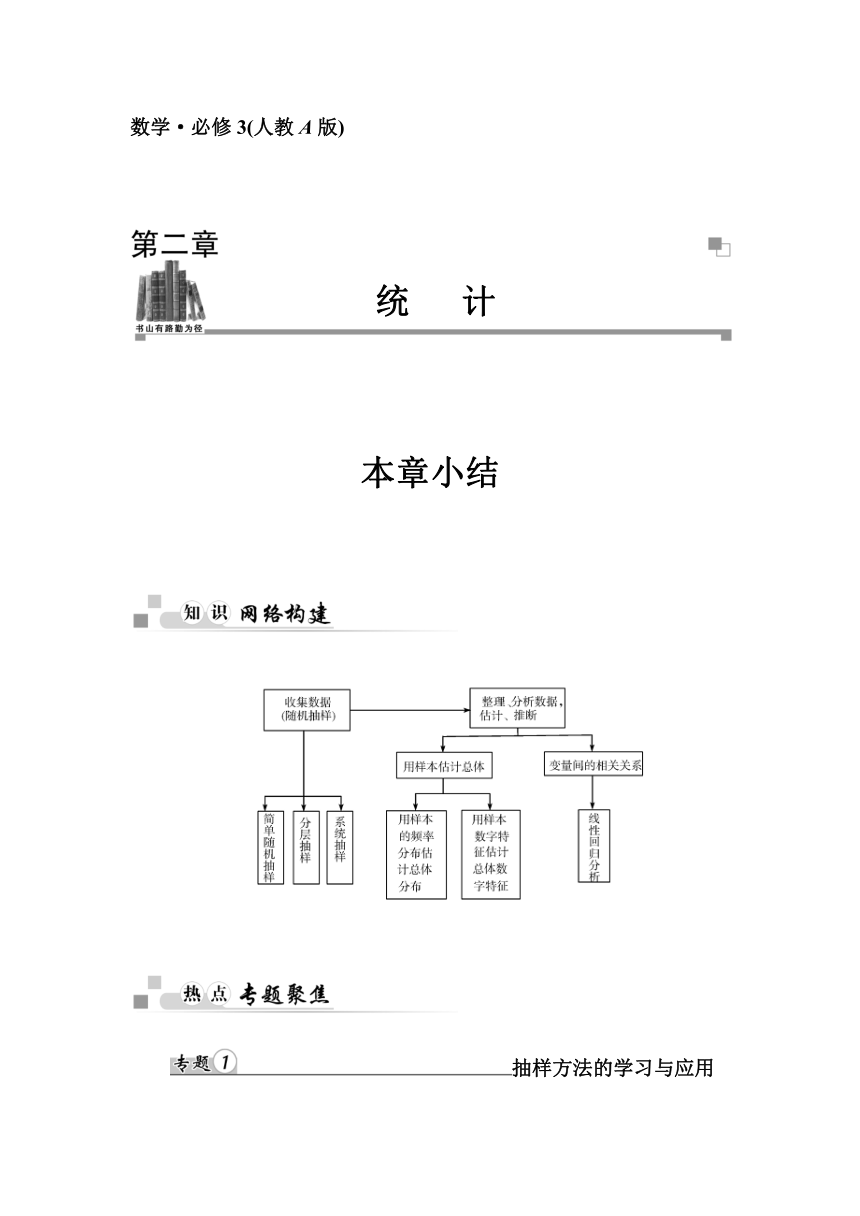 | |
| 格式 | zip | ||
| 文件大小 | 426.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-20 20:02:48 | ||
图片预览





文档简介
数学·必修3(人教A版)
本章小结
抽样方法的学习与应用
专题归纳
三种抽样方法的概念和抽样方法的具体实施以及三种抽样方法的区别与联系是本部分的基础知识和重要内容.三种抽样方法的特点:
(1)简单随机抽样.
①要求被抽取样本的总体的个数有限,以便于 ( http: / / www.21cnjy.com )对其中各个个体被抽取的可能性进行分析,一般地,从个体数为N的总体中抽取一个容量为n的样本,每个个体被抽取的机会是均等的.
②从总体中逐个不放回地抽取,易操作,且抽样方法比较简单,所以成为其他较复杂的抽样方法的基础.
③简单随机抽样体现了抽样的客观性与公平性.
(2)系统抽样.
①系统抽样与简单随机抽样的联系在于:在总体均分后的每一部分进行抽样时,采用的是简单随机抽样.
②整个抽样过程中,每个个体被抽取的机会均等.
(3)分层抽样.
①它适用于总体由差异明显的几部分组成的情况.
②在每一层进行抽样时,采用简单随机抽样或系统抽样.
③分层抽样充分利用已掌握的信息,使样本具有良好的代表性.
分层抽样也是机会均等抽样,而且在每层抽样时,可以根据具体情况采用不同的抽样方法,因此应用较为广泛.
例题分析
一批产品,有一级品100个,二级品60个,三级品40个,分别用系统抽样和分层抽样方法,从这批产品中抽取一容量为20的样本.
解析:系统抽样方法:将200个产品编号后, ( http: / / www.21cnjy.com )随机地分为20个组,每组10个产品,从号码为1~10的第一组中随机抽取1个号码,假如抽到的是6号,然后从6号开始,每隔10个号码抽取1个,得到6,16,26,…,196,这样就得到容量为20的一个样本.
分层抽样方法:∵一、二、三级品的个数之比为 ( http: / / www.21cnjy.com )5∶3∶2,∴需要从一级品中抽取×20=10(个),二级品中抽取×20=6(个),三级品中抽到×20=4(个).
跟踪训练
1.某服装厂平均每小时大约生产服装362件,要求质检员每小时抽取40件服装检验其质量状况,请你设计一个调查方案.
解析:因为总体中的个体数较多,并且总体是由没有明显差异的个体组成,所以本题宜采用系统抽样法.
第一步,把这些服装分成40组,由于的商是9,余数是2,所以每个组有9件服装还剩2件服装,这时分段间隔就是9.
第二步,先用简单随机抽样的方法从这些服装中抽取2件服装不进行检验.
第三步,将剩下的服装进行编号,编号分别为0,1,2,…,359.
第四步,从第一组(编号分别为0,1,…,8)的服装中按照简单随机抽样的方法抽取1件服装,比如,编号为k.
第五步,依次抽取编号分别为下面数字的服装k,k+9,k+18,k+27,…,k+39×9,这样就抽取了一个容量为40的样本.
2.在120个零件中,一级品24个,二级品36个,三级品60个,从中抽取容量为20的样本,则总体中每个个体被抽取的机会是多少?
解析:因为总体中的个体数N=120,样本容量n=20,故每个个体被抽取的机会为.
3.经问卷调查,某班学生对 ( http: / / www.21cnjy.com )摄影分别执“喜欢”、“不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢”态度的多12人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的5位“喜欢”摄影的同学、1位“不喜欢”摄影的同学和3位执“一般”态度的同学,那么全班学生中“喜欢”摄影的比全班人数的一半还多________人.
解析:设班里“喜欢”摄影的同学有y人,“一般”的有x人,“不喜欢”的有x-12人,则 解得
∴全班共有30+18+6=54人,又30-=3.
∴“喜欢”摄影的比全班人数的一半还多3人.
答案:3
统计图、表及其应用
专题归纳
收集、整理与分析以及处理数据的能力是信 ( http: / / www.21cnjy.com )息时代每一个公民基本素养的一部分.统计所提供的“运用数据进行推断”的思考方法已经成为现代社会一种普遍适用并且强有力的思维方式.统计图表就是表达和分析数据的重要工具,它不仅可以帮助我们从数据中获得有用的信息,还可以帮助我们直观、准确地理解相应的结果.用样本估计总体的方法在高中数学中主要有频率分布表、频率分布直方图、频率分布折线图、总体密度曲线、茎叶图等.
例题分析
为了保护学生视力,教室内的日光灯在使用一段时间后必须更换,已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
天数/天 151~180 181~210 211~240 241~270 271~300 301~330 331~360 361~390
灯管数/只 1 11 18 20 25 16 7 2
试估计这种日光灯的平均使用寿命.若定期更换,可选择多长时间统一更换合适?
解析:总体的平均数与标准差往往是很难求的,甚至是不可求的,通常的做法是用样本的平均数与标准差去估计总体的平均数与标准差.
各组中值分别为165,195,225,255,285,315,345,375,由此可算得平均数约为:
165×1%+195×11%+22 ( http: / / www.21cnjy.com )5×18%+255×20%+285×25%+315×16%+345×7%+375×2%=267.9≈268(天).
将组中值对于此平均数求方差得:
×=2 128.60(天2)
故标准差为≈46(天).
答:估计这种日光灯的平均使用寿命约为268天,标准差约为46天,故可在222天到314天左右统一更换较合适.
甲、乙两人在相同条件下打靶十次,每次打靶的成绩情况如下图:
(1)请填写下表:
平均数 中位数 命中9环以上次数
甲 7
乙
(2)从下列三个不同角度对这次测验结果进行分析:
从平均数和中位数相结合看,谁的成绩好些?
从平均数和命中9环以上的次数相结合看,谁的成绩好些?
从折线图两人射击命中环数的走势看,谁更有潜力?
解析:(1)甲的数据为:2,4,6 ( http: / / www.21cnjy.com ),7,7,8,8,9,9,10,所以甲的中位数为7.5,命中9环以上次数为3.乙的数据为:5,6,6,7,7,7,7,8,8,9,所以乙的平均数为7,乙的中位数为7,命中9环以上次数为1.
(2)从平均数和中位数相结合看,甲成绩比乙稳 ( http: / / www.21cnjy.com )定;从平均数和命中9环以上的次数相结合看,甲成绩比乙好一些;从折线图两人射击命中环数的走势看,甲的潜力更大一些.
跟踪训练
4.某公司销售部有营销人员15人,销售部为了制订某种商品的月销售定额,统计了这15人某月的销售量(如下表):
每人销售件数/件 1800 510 250 210 150 120
人数/人 1 1 3 5 3 2
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)假设销售部负责人把每位营销人员的月销售额定为320件,你认为是否合理,为什么?如不合理,请你制订一个较合理的销售定额.
解析:(1)由表可知平均数 ( http: / / www.21cnjy.com )=(1 800×1+510×1+250×3+210×5+150×3+120×2)=320(件).中位数为210(件),众数为210(件).
(2)不合理.因为15人 ( http: / / www.21cnjy.com )中就有13人的销售额达不到320件,也就是说320虽是这一组数据的平均数,但它却不能反映营销人员的一般水平.销售额定为210件要合理些.这是由于210既是中位数,又是众数,是绝大部分人都能达到的定额.
5.公交车的数量太多容易造成资源的浪费 ( http: / / www.21cnjy.com ),太少又难以满足乘客的需求.为此,公交公司在某站台随机调查了80名乘客,他们的候车时间如下所示(单位:分):
17 14 20 12 10 24 18 17 1 22
13 19 28 5 34 7 25 18 28 1
15 31 12 11 10 16 12 9 10 13
19 10 12 12 16 22 17 23 16 15
16 11 9 3 13 2 18 22 19 9
23 28 15 21 28 12 11 14 15 3
11 6 2 18 25 5 12 15 20 16
12 28 20 12 28 15 8 32 18 9
(1)将数据进行适当的分组,并画出相应的频率分布直方图和频率折线图.
(2)这80名乘客候车时间的平均数是多少?标准差呢?
(3)你能为公交公司提出什么建议?
解析:
时间分组 频数 频率
[0,5) 6 0.075
[5,10) 9 0.1 175
[10,15) 22 0.275
[15,20) 22 0.275
[20,25) 10 0.125
[25,30) 8 0.100
[30,35) 3 0.0 375
频率分布直方图如下所示:
频率折线图如下所示:
(2)这80名乘客候车时间的平均数是15.475 min,标准差约是7.5.
(3)公交公司可以适当增加公交车的数量.
回归分析及其应用
专题归纳
回归分析是对具有相关关系的两个变量进行 ( http: / / www.21cnjy.com )统计分析的一种常用方法.相关性问题是日常生活中普遍存在的问题.生活中有些变量之间存在着明显的函数关系,有些变量之间不满足函数关系,但是它们之间又存在着一种明显的依赖关系.
利用回归分析的方法对两个具有线性相关关系的变量研究的步骤为:
(1)画出这两个变量的散点图;
(2)求回归直线方程;
(3)利用回归直线方程进行预报.
某农场对单位面积化肥用量x(kg)和水稻相应产量y(kg)的关系作了统计,得到数据如下:
x 15 20 25 30 35 40 45
y 330 345 365 405 445 450 455
如果x与y之间具有线性相关关系,求出回归直线方程,并预测当单位面积化肥用量为32 kg时,水稻的产量大约是多少(精确到0.01 kg)
解析:用列表的方法计算a与回归系数b.
序号 x y x2 xy
1 15 330 225 4 950
2 20 345 400 6 900
3 25 365 625 9 125
4 30 405 900 12 150
5 35 445 1 225 15 575
6 40 450 1 600 18 000
7 45 455 2 025 20 475
=×(15+20+…+45)=30,
=×(330+345+…+455)≈399.3,
∑x=225+400+…+2 025=7 000,
∑xiyi=4 950+6 900+…+20 475=87 175,
=≈4.746,
=399.3-4.746×30=256.92.
y对x的回归直线方程为=+x=256.92+4.746x.
当x=32时,=256.92+4.746×32≈408.79.
故所求回归直线方程为=256.92+4.746x.当单位面积化肥用量为32 kg时,水稻的产量大约为408.79 kg.
跟踪训练
6.高三(1)班学生每周用于数学学习的时间x(单位:h)与数学成绩y(单位:分)之间有如下数据:
x 24 15 23 19 16 11 20 16 17 13
y 92 79 97 89 64 47 83 68 71 59
某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
解析:两个有相关关系的变量间的关系可以用线性回归方程来表示,而对总体的预测可由回归直线方程帮助解决.
因为学习时间与学习成绩间有相关关系,可以列出下表,并用计算器进行计算.
i 1 2 3 4 5 6 7 8 9 10
xi 24 15 23 19 16 11 20 16 17 13
yi 92 79 97 89 64 47 83 68 71 59
xiyi 2 208 1 185 2 231 1 691 1 024 517 1 660 1 088 1 207 767
=17.4, =74.9,=3 182,iyi=13 578
于是可得==≈3.53,
=-=74.9-3.53×17.4≈13.5,
因此可求得回归直线方程=3.53x+13.5,
当x=18时,=3.53×18+13.5=77.04≈77,
故该同学预计可得77分左右.
统 计
本章小结
抽样方法的学习与应用
专题归纳
三种抽样方法的概念和抽样方法的具体实施以及三种抽样方法的区别与联系是本部分的基础知识和重要内容.三种抽样方法的特点:
(1)简单随机抽样.
①要求被抽取样本的总体的个数有限,以便于 ( http: / / www.21cnjy.com )对其中各个个体被抽取的可能性进行分析,一般地,从个体数为N的总体中抽取一个容量为n的样本,每个个体被抽取的机会是均等的.
②从总体中逐个不放回地抽取,易操作,且抽样方法比较简单,所以成为其他较复杂的抽样方法的基础.
③简单随机抽样体现了抽样的客观性与公平性.
(2)系统抽样.
①系统抽样与简单随机抽样的联系在于:在总体均分后的每一部分进行抽样时,采用的是简单随机抽样.
②整个抽样过程中,每个个体被抽取的机会均等.
(3)分层抽样.
①它适用于总体由差异明显的几部分组成的情况.
②在每一层进行抽样时,采用简单随机抽样或系统抽样.
③分层抽样充分利用已掌握的信息,使样本具有良好的代表性.
分层抽样也是机会均等抽样,而且在每层抽样时,可以根据具体情况采用不同的抽样方法,因此应用较为广泛.
例题分析
一批产品,有一级品100个,二级品60个,三级品40个,分别用系统抽样和分层抽样方法,从这批产品中抽取一容量为20的样本.
解析:系统抽样方法:将200个产品编号后, ( http: / / www.21cnjy.com )随机地分为20个组,每组10个产品,从号码为1~10的第一组中随机抽取1个号码,假如抽到的是6号,然后从6号开始,每隔10个号码抽取1个,得到6,16,26,…,196,这样就得到容量为20的一个样本.
分层抽样方法:∵一、二、三级品的个数之比为 ( http: / / www.21cnjy.com )5∶3∶2,∴需要从一级品中抽取×20=10(个),二级品中抽取×20=6(个),三级品中抽到×20=4(个).
跟踪训练
1.某服装厂平均每小时大约生产服装362件,要求质检员每小时抽取40件服装检验其质量状况,请你设计一个调查方案.
解析:因为总体中的个体数较多,并且总体是由没有明显差异的个体组成,所以本题宜采用系统抽样法.
第一步,把这些服装分成40组,由于的商是9,余数是2,所以每个组有9件服装还剩2件服装,这时分段间隔就是9.
第二步,先用简单随机抽样的方法从这些服装中抽取2件服装不进行检验.
第三步,将剩下的服装进行编号,编号分别为0,1,2,…,359.
第四步,从第一组(编号分别为0,1,…,8)的服装中按照简单随机抽样的方法抽取1件服装,比如,编号为k.
第五步,依次抽取编号分别为下面数字的服装k,k+9,k+18,k+27,…,k+39×9,这样就抽取了一个容量为40的样本.
2.在120个零件中,一级品24个,二级品36个,三级品60个,从中抽取容量为20的样本,则总体中每个个体被抽取的机会是多少?
解析:因为总体中的个体数N=120,样本容量n=20,故每个个体被抽取的机会为.
3.经问卷调查,某班学生对 ( http: / / www.21cnjy.com )摄影分别执“喜欢”、“不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢”态度的多12人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的5位“喜欢”摄影的同学、1位“不喜欢”摄影的同学和3位执“一般”态度的同学,那么全班学生中“喜欢”摄影的比全班人数的一半还多________人.
解析:设班里“喜欢”摄影的同学有y人,“一般”的有x人,“不喜欢”的有x-12人,则 解得
∴全班共有30+18+6=54人,又30-=3.
∴“喜欢”摄影的比全班人数的一半还多3人.
答案:3
统计图、表及其应用
专题归纳
收集、整理与分析以及处理数据的能力是信 ( http: / / www.21cnjy.com )息时代每一个公民基本素养的一部分.统计所提供的“运用数据进行推断”的思考方法已经成为现代社会一种普遍适用并且强有力的思维方式.统计图表就是表达和分析数据的重要工具,它不仅可以帮助我们从数据中获得有用的信息,还可以帮助我们直观、准确地理解相应的结果.用样本估计总体的方法在高中数学中主要有频率分布表、频率分布直方图、频率分布折线图、总体密度曲线、茎叶图等.
例题分析
为了保护学生视力,教室内的日光灯在使用一段时间后必须更换,已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
天数/天 151~180 181~210 211~240 241~270 271~300 301~330 331~360 361~390
灯管数/只 1 11 18 20 25 16 7 2
试估计这种日光灯的平均使用寿命.若定期更换,可选择多长时间统一更换合适?
解析:总体的平均数与标准差往往是很难求的,甚至是不可求的,通常的做法是用样本的平均数与标准差去估计总体的平均数与标准差.
各组中值分别为165,195,225,255,285,315,345,375,由此可算得平均数约为:
165×1%+195×11%+22 ( http: / / www.21cnjy.com )5×18%+255×20%+285×25%+315×16%+345×7%+375×2%=267.9≈268(天).
将组中值对于此平均数求方差得:
×=2 128.60(天2)
故标准差为≈46(天).
答:估计这种日光灯的平均使用寿命约为268天,标准差约为46天,故可在222天到314天左右统一更换较合适.
甲、乙两人在相同条件下打靶十次,每次打靶的成绩情况如下图:
(1)请填写下表:
平均数 中位数 命中9环以上次数
甲 7
乙
(2)从下列三个不同角度对这次测验结果进行分析:
从平均数和中位数相结合看,谁的成绩好些?
从平均数和命中9环以上的次数相结合看,谁的成绩好些?
从折线图两人射击命中环数的走势看,谁更有潜力?
解析:(1)甲的数据为:2,4,6 ( http: / / www.21cnjy.com ),7,7,8,8,9,9,10,所以甲的中位数为7.5,命中9环以上次数为3.乙的数据为:5,6,6,7,7,7,7,8,8,9,所以乙的平均数为7,乙的中位数为7,命中9环以上次数为1.
(2)从平均数和中位数相结合看,甲成绩比乙稳 ( http: / / www.21cnjy.com )定;从平均数和命中9环以上的次数相结合看,甲成绩比乙好一些;从折线图两人射击命中环数的走势看,甲的潜力更大一些.
跟踪训练
4.某公司销售部有营销人员15人,销售部为了制订某种商品的月销售定额,统计了这15人某月的销售量(如下表):
每人销售件数/件 1800 510 250 210 150 120
人数/人 1 1 3 5 3 2
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)假设销售部负责人把每位营销人员的月销售额定为320件,你认为是否合理,为什么?如不合理,请你制订一个较合理的销售定额.
解析:(1)由表可知平均数 ( http: / / www.21cnjy.com )=(1 800×1+510×1+250×3+210×5+150×3+120×2)=320(件).中位数为210(件),众数为210(件).
(2)不合理.因为15人 ( http: / / www.21cnjy.com )中就有13人的销售额达不到320件,也就是说320虽是这一组数据的平均数,但它却不能反映营销人员的一般水平.销售额定为210件要合理些.这是由于210既是中位数,又是众数,是绝大部分人都能达到的定额.
5.公交车的数量太多容易造成资源的浪费 ( http: / / www.21cnjy.com ),太少又难以满足乘客的需求.为此,公交公司在某站台随机调查了80名乘客,他们的候车时间如下所示(单位:分):
17 14 20 12 10 24 18 17 1 22
13 19 28 5 34 7 25 18 28 1
15 31 12 11 10 16 12 9 10 13
19 10 12 12 16 22 17 23 16 15
16 11 9 3 13 2 18 22 19 9
23 28 15 21 28 12 11 14 15 3
11 6 2 18 25 5 12 15 20 16
12 28 20 12 28 15 8 32 18 9
(1)将数据进行适当的分组,并画出相应的频率分布直方图和频率折线图.
(2)这80名乘客候车时间的平均数是多少?标准差呢?
(3)你能为公交公司提出什么建议?
解析:
时间分组 频数 频率
[0,5) 6 0.075
[5,10) 9 0.1 175
[10,15) 22 0.275
[15,20) 22 0.275
[20,25) 10 0.125
[25,30) 8 0.100
[30,35) 3 0.0 375
频率分布直方图如下所示:
频率折线图如下所示:
(2)这80名乘客候车时间的平均数是15.475 min,标准差约是7.5.
(3)公交公司可以适当增加公交车的数量.
回归分析及其应用
专题归纳
回归分析是对具有相关关系的两个变量进行 ( http: / / www.21cnjy.com )统计分析的一种常用方法.相关性问题是日常生活中普遍存在的问题.生活中有些变量之间存在着明显的函数关系,有些变量之间不满足函数关系,但是它们之间又存在着一种明显的依赖关系.
利用回归分析的方法对两个具有线性相关关系的变量研究的步骤为:
(1)画出这两个变量的散点图;
(2)求回归直线方程;
(3)利用回归直线方程进行预报.
某农场对单位面积化肥用量x(kg)和水稻相应产量y(kg)的关系作了统计,得到数据如下:
x 15 20 25 30 35 40 45
y 330 345 365 405 445 450 455
如果x与y之间具有线性相关关系,求出回归直线方程,并预测当单位面积化肥用量为32 kg时,水稻的产量大约是多少(精确到0.01 kg)
解析:用列表的方法计算a与回归系数b.
序号 x y x2 xy
1 15 330 225 4 950
2 20 345 400 6 900
3 25 365 625 9 125
4 30 405 900 12 150
5 35 445 1 225 15 575
6 40 450 1 600 18 000
7 45 455 2 025 20 475
=×(15+20+…+45)=30,
=×(330+345+…+455)≈399.3,
∑x=225+400+…+2 025=7 000,
∑xiyi=4 950+6 900+…+20 475=87 175,
=≈4.746,
=399.3-4.746×30=256.92.
y对x的回归直线方程为=+x=256.92+4.746x.
当x=32时,=256.92+4.746×32≈408.79.
故所求回归直线方程为=256.92+4.746x.当单位面积化肥用量为32 kg时,水稻的产量大约为408.79 kg.
跟踪训练
6.高三(1)班学生每周用于数学学习的时间x(单位:h)与数学成绩y(单位:分)之间有如下数据:
x 24 15 23 19 16 11 20 16 17 13
y 92 79 97 89 64 47 83 68 71 59
某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
解析:两个有相关关系的变量间的关系可以用线性回归方程来表示,而对总体的预测可由回归直线方程帮助解决.
因为学习时间与学习成绩间有相关关系,可以列出下表,并用计算器进行计算.
i 1 2 3 4 5 6 7 8 9 10
xi 24 15 23 19 16 11 20 16 17 13
yi 92 79 97 89 64 47 83 68 71 59
xiyi 2 208 1 185 2 231 1 691 1 024 517 1 660 1 088 1 207 767
=17.4, =74.9,=3 182,iyi=13 578
于是可得==≈3.53,
=-=74.9-3.53×17.4≈13.5,
因此可求得回归直线方程=3.53x+13.5,
当x=18时,=3.53×18+13.5=77.04≈77,
故该同学预计可得77分左右.
统 计
