27.2.2 相似三角形的性质一课一练(含解析)
文档属性
| 名称 | 27.2.2 相似三角形的性质一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 22:52:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
27.2.2 相似三角形的性质一课一练
一、单选题
1.如图,△ABC∽△ADE , 则下列比例式正确的是( )
A. B. C. D.
2.两个相似三角形的相似比为1:2,则它们面积的比为( )
A.1:4 B.1:2 C.1: D.4:1
3.若△ABC∽△A′B′C′且 = ,△ABC的周长为15cm,则△A′B′C′的周长为( )cm.
A.18 B.20 C. D.
4.△ABC与△A'B'C'是位似图形,且△ABC与△A'B'C'位似比是1:2,已知△ABC的面积是10,则△A'B'C'的面积是( )
A.10 B.20 C.40 D.80
二、填空题
5.若两个相似三角形的相似比为3∶4,则它们的面积比为 .
6.如图,在四边形 中, 于点 , ,且 ,当 , 时,线段 的长度为 .
三、计算题
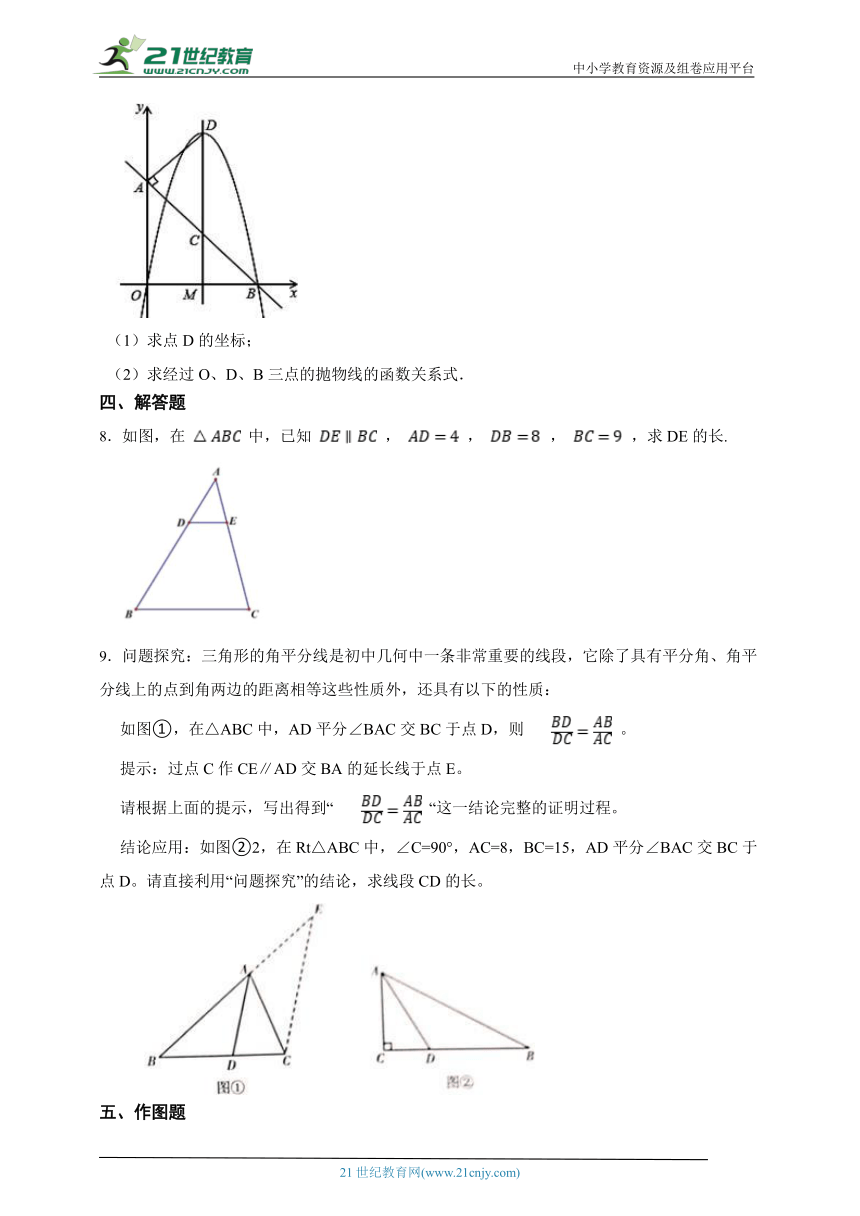
7.如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.
(1)求点D的坐标;
(2)求经过O、D、B三点的抛物线的函数关系式.
四、解答题
8.如图,在 中,已知 , , , ,求DE的长.
9.问题探究:三角形的角平分线是初中几何中一条非常重要的线段,它除了具有平分角、角平分线上的点到角两边的距离相等这些性质外,还具有以下的性质:
如图①,在△ABC中,AD平分∠BAC交BC于点D,则 。
提示:过点C作CE∥AD交BA的延长线于点E。
请根据上面的提示,写出得到“ “这一结论完整的证明过程。
结论应用:如图②2,在Rt△ABC中,∠C=90°,AC=8,BC=15,AD平分∠BAC交BC于点D。请直接利用“问题探究”的结论,求线段CD的长。
五、作图题
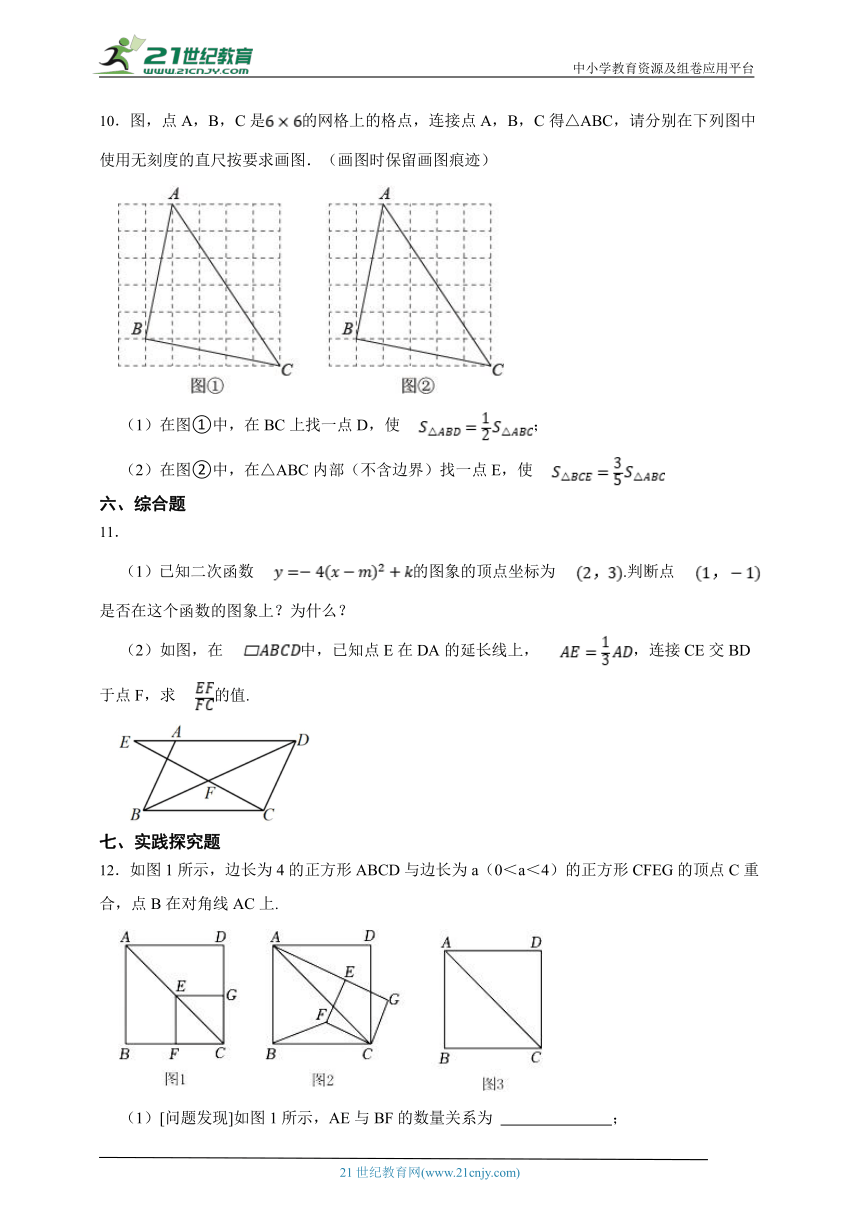
10.图,点A,B,C是的网格上的格点,连接点A,B,C得△ABC,请分别在下列图中使用无刻度的直尺按要求画图.(画图时保留画图痕迹)
(1)在图①中,在BC上找一点D,使;
(2)在图②中,在△ABC内部(不含边界)找一点E,使
六、综合题
11.
(1)已知二次函数的图象的顶点坐标为.判断点是否在这个函数的图象上?为什么?
(2)如图,在中,已知点E在DA的延长线上,,连接CE交BD于点F,求的值.
七、实践探究题
12.如图1所示,边长为4的正方形ABCD与边长为a(0<a<4)的正方形CFEG的顶点C重合,点B在对角线AC上.
(1)[问题发现]如图1所示,AE与BF的数量关系为 ;
(2)[类比探究]如图2所示,将正方形CFEG绕点C旋转,旋转角为α(0<α<30°),请问此时上述结论是否还成立?若成立,写出推理过程,若不成立,说明理由;
(3)[拓展延伸]当a=时,正方形CFEG若按图1所示位置开始旋转,在正方形CFEG的旋转过程中,当点A、F、C在一条直线上时,求出此时线段AE的长.
答案解析部分
1.【答案】D
【解析】【解答】∵△ABC∽△ADE , ∴ ,
故答案为:D.
【分析】本题考查相似三角形的性质,掌握相似三角形的对应边成比例这一性质是解答此题的关键.
2.【答案】A
【解析】【解答】∵两个相似三角形的相似比为1:2,
∴它们面积的比等于: .
故答案为:A.
【分析】根据相似三角形的性质“相似三角形的面积的比等于相似比的平方”可求解.
3.【答案】B
【解析】【解答】∵△ABC∽△A′B′C′,
∴ = =
∴ = = ,
∵△ABC的周长为15cm,
∴△A′B′C′的周长为20cm.
故选B.
【分析】根据比例的等比性质可得相似三角形周长的比等于相似比,可得 = = ,由△ABC的周长为15cm,即可求得△A′B′C′的周长.
4.【答案】A
【解析】【解答】解:∵两个三嘉兴的位似比为1:2
∴两个三角形的为1:4
∵△ABC的面积为10
∴△A'B'C'面积为20
故答案为:B.
【分析】根据相似三角形的性质,计算得到答案即可。
5.【答案】9:16
【解析】【解答】解:∵两个相似五边形的相似比为3:4,
∴它们的面积比为9:16
故答案为9:16
【分析】相似多边形的面积比等于相似比的平方,据此解答即可.
6.【答案】
【解析】【解答】解:如图,在
上截取
,过
作
交
于点
,把
绕
逆时针旋转得
,连接
,
则
,
,
,
∴ ,
又∵ 于点
,
,
,
∴ ,
∴ ,
又∵ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
又
,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴在
中,由勾股定理得,
,
∴ .
故答案为:
.
【分析】在
上截取
,过
作
交
于点
,把
绕
逆时针旋转得
,连接
,易求
,然后证明
,可得
,再证
可得
,由
可得
,从而求出MN=
,证得
,可求出
,在
中,由勾股定理求出CE,利用
即可求解.
7.【答案】(1)如图,过点D作DE⊥OA于E,
在△AED与△BAO中
∵∠EDA+∠EAD=∠EAD+∠BAO=90°,
∴∠EDA=∠BAO,
∵∠AED=∠AOB=90°,
∴△ADE∽△BAO,
∴
∵点A(0,4),DM=6,
∴AO=4,AE=EO-AO=DM-AO=2,
∴ED=,
∴点D的坐标为D(2,6).
(2)∵AE=2,ED=2,△ADE∽△BAO,
∴BO=AO=4
∴点B的坐标为B(4,0)
设:过O、D、B三点的抛物线的函数关系式为:
将O(0,0),B(0,4),D(2,6)代入函数关系式,解得:
∴过O、D、B三点的抛物线的函数关系式为:.
【解析】【分析】(1)过点D作DE⊥OA于E,可得到:△ADE∽△BAO,根据相似三角形的对应边成比例可求得点D坐标;
(2)根据△ADE∽△BAO,且AE=2,ED=2,可以得到:点B的坐标为B(0,4).设出函数解析式,将O、D、B三点坐标代入即可求出解析式.
8.【答案】解:∵AD=4,DB=8,
∴AB=12,
∵DE∥BC,
∴△ADE∽△ABC,
∴ ,即 ,
∴DE=3.
【解析】【分析】由DE∥BC,判断△ADE∽△ABC,再由相似三角形的性质得出相似比求DE.
9.【答案】解:问题探究:过点C作CE∥AD交BA的延长线于点E, ∴ ,∠BAD=∠E,∠CAD=∠ACE. ∵AD平分∠BAC,∴∠BAD=∠CAD. ∴∠E=∠ACE.∴AC= AE. ∴ . 结论应用:在Rt△ABC中,∠C=90°, . 设CD的长为x,则BD的长为15-x. ∵AD平分∠BAC, ∴ ,即 . 解得 . ∴CD的长为 .
【解析】【分析】 过点C作CE∥AD交BA的延长线于点E,则 ,根据“双平等腰”模型,易证 AC=AE,进而即可得到结论;根据勾股定理,求出AB的长, 设CD的长为x,则BD的长为15-x. 根据角平分线的性质,列出方程,即可求解.
10.【答案】(1)解:如图所示,取格点G、H,连接GH交BC于D,点D即为所求;
∵四边形BGCH是矩形,
∴点D是BC的中点,
∴;
(2)解:如图所示,取格点M、T、H、N,连接MN交AB于P,连接TH交AC于Q,连接PQ,
在线段PQ上任取一点E(不包括端点)即为所求;
由图知,,
∴,
∴∠ABC=90°,
∴,
∵,
∴△MNE∽△PQE,
∴,
∴,
同理可证,
∴,
又∵∠PAQ=∠BAC,
∴△APQ∽△ABC,
∴∠APQ=∠ABC,
∴,
∴.
【解析】【分析】根据要求作出图象即可。
11.【答案】(1)解:点在这个函数的图象上.理由如下:
∵二次函数的图象的顶点坐标为,
∴二次函数的解析式为,
∴当时,.
∴点在这个函数的图象上.
(2)解:∵在中,
∴BC=AD.
∵ED//BC,
∴△EDF∽△CBF,
∴,
又∵,
∴,
∴.
∴.
【解析】【分析】(1)由题意先把顶点坐标代入抛物线的解析式,然后把点(1,-1)代入所求的解析式验证即可判断求解;
(2)由平行四边形的性质可得BC=AD,根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得△EDF∽△CBF,于是可得比例式并结合已知即可求解.
12.【答案】(1)AE= BF
(2)解:上述结成立,理由如下:
连接CE,如图2所示:
∵∠FCE=∠BCA=45°,
∴∠BCF=∠ACE=45°﹣∠ACF,
在Rt△CEF和Rt△CBA中,CE= CF,CA= CB,
∴ = ,
∴△ACE∽△BCF,
∴ = ,
∴AE= BF;
(3)解:如图3﹣1中,当点F落在AC上时,
∵AB=CB=4,∠B=90°,
∴AC= AB=4 ,
∵CF=EF= ,
∴AF=3 ,
∵∠AFE=90°,
∴AE= .
如图3﹣2中,当点F落在AC的延长线上时,同法可得AE= .
综上所述,AE的长为2 或2 .
故答案为:2 或2 .
【解析】【解答】解:(1)结论:AE= BF,理由如下:
∵四边形ABCD和四边形CFEG是正方形,
∴∠B=∠CFE=90°,∠FCE=∠BCA=45°,CE= CF,CE⊥GF,
∴AB∥EF,
∴ = ,
∴AE= BF;
故答案为:AE= BF;
【分析】(1)根据正方形的性质可得∠B=∠CFE=90°,∠FCE=∠BCA=45°,CE=CF,CE⊥GF,则AB∥EF,然后根据平行线分线段成比例的性质进行解答;
(2)连接CE,根据角的和差关系可得∠BCF=∠ACE,易得=,证明△ACE∽△BCF,然后根据相似三角形的性质进行解答;
(3)当点F落在AC上时,由勾股定理可得AC=AB=4,则AF=AC-CF=3,然后利用勾股定理就可求出AE的值;当点F落在AC的延长线上时,同法可得AE.
27.2.2 相似三角形的性质一课一练
一、单选题
1.如图,△ABC∽△ADE , 则下列比例式正确的是( )
A. B. C. D.
2.两个相似三角形的相似比为1:2,则它们面积的比为( )
A.1:4 B.1:2 C.1: D.4:1
3.若△ABC∽△A′B′C′且 = ,△ABC的周长为15cm,则△A′B′C′的周长为( )cm.
A.18 B.20 C. D.
4.△ABC与△A'B'C'是位似图形,且△ABC与△A'B'C'位似比是1:2,已知△ABC的面积是10,则△A'B'C'的面积是( )
A.10 B.20 C.40 D.80
二、填空题
5.若两个相似三角形的相似比为3∶4,则它们的面积比为 .
6.如图,在四边形 中, 于点 , ,且 ,当 , 时,线段 的长度为 .
三、计算题
7.如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.
(1)求点D的坐标;
(2)求经过O、D、B三点的抛物线的函数关系式.
四、解答题
8.如图,在 中,已知 , , , ,求DE的长.
9.问题探究:三角形的角平分线是初中几何中一条非常重要的线段,它除了具有平分角、角平分线上的点到角两边的距离相等这些性质外,还具有以下的性质:
如图①,在△ABC中,AD平分∠BAC交BC于点D,则 。
提示:过点C作CE∥AD交BA的延长线于点E。
请根据上面的提示,写出得到“ “这一结论完整的证明过程。
结论应用:如图②2,在Rt△ABC中,∠C=90°,AC=8,BC=15,AD平分∠BAC交BC于点D。请直接利用“问题探究”的结论,求线段CD的长。
五、作图题
10.图,点A,B,C是的网格上的格点,连接点A,B,C得△ABC,请分别在下列图中使用无刻度的直尺按要求画图.(画图时保留画图痕迹)
(1)在图①中,在BC上找一点D,使;
(2)在图②中,在△ABC内部(不含边界)找一点E,使
六、综合题
11.
(1)已知二次函数的图象的顶点坐标为.判断点是否在这个函数的图象上?为什么?
(2)如图,在中,已知点E在DA的延长线上,,连接CE交BD于点F,求的值.
七、实践探究题
12.如图1所示,边长为4的正方形ABCD与边长为a(0<a<4)的正方形CFEG的顶点C重合,点B在对角线AC上.
(1)[问题发现]如图1所示,AE与BF的数量关系为 ;
(2)[类比探究]如图2所示,将正方形CFEG绕点C旋转,旋转角为α(0<α<30°),请问此时上述结论是否还成立?若成立,写出推理过程,若不成立,说明理由;
(3)[拓展延伸]当a=时,正方形CFEG若按图1所示位置开始旋转,在正方形CFEG的旋转过程中,当点A、F、C在一条直线上时,求出此时线段AE的长.
答案解析部分
1.【答案】D
【解析】【解答】∵△ABC∽△ADE , ∴ ,
故答案为:D.
【分析】本题考查相似三角形的性质,掌握相似三角形的对应边成比例这一性质是解答此题的关键.
2.【答案】A
【解析】【解答】∵两个相似三角形的相似比为1:2,
∴它们面积的比等于: .
故答案为:A.
【分析】根据相似三角形的性质“相似三角形的面积的比等于相似比的平方”可求解.
3.【答案】B
【解析】【解答】∵△ABC∽△A′B′C′,
∴ = =
∴ = = ,
∵△ABC的周长为15cm,
∴△A′B′C′的周长为20cm.
故选B.
【分析】根据比例的等比性质可得相似三角形周长的比等于相似比,可得 = = ,由△ABC的周长为15cm,即可求得△A′B′C′的周长.
4.【答案】A
【解析】【解答】解:∵两个三嘉兴的位似比为1:2
∴两个三角形的为1:4
∵△ABC的面积为10
∴△A'B'C'面积为20
故答案为:B.
【分析】根据相似三角形的性质,计算得到答案即可。
5.【答案】9:16
【解析】【解答】解:∵两个相似五边形的相似比为3:4,
∴它们的面积比为9:16
故答案为9:16
【分析】相似多边形的面积比等于相似比的平方,据此解答即可.
6.【答案】
【解析】【解答】解:如图,在
上截取
,过
作
交
于点
,把
绕
逆时针旋转得
,连接
,
则
,
,
,
∴ ,
又∵ 于点
,
,
,
∴ ,
∴ ,
又∵ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
又
,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴在
中,由勾股定理得,
,
∴ .
故答案为:
.
【分析】在
上截取
,过
作
交
于点
,把
绕
逆时针旋转得
,连接
,易求
,然后证明
,可得
,再证
可得
,由
可得
,从而求出MN=
,证得
,可求出
,在
中,由勾股定理求出CE,利用
即可求解.
7.【答案】(1)如图,过点D作DE⊥OA于E,
在△AED与△BAO中
∵∠EDA+∠EAD=∠EAD+∠BAO=90°,
∴∠EDA=∠BAO,
∵∠AED=∠AOB=90°,
∴△ADE∽△BAO,
∴
∵点A(0,4),DM=6,
∴AO=4,AE=EO-AO=DM-AO=2,
∴ED=,
∴点D的坐标为D(2,6).
(2)∵AE=2,ED=2,△ADE∽△BAO,
∴BO=AO=4
∴点B的坐标为B(4,0)
设:过O、D、B三点的抛物线的函数关系式为:
将O(0,0),B(0,4),D(2,6)代入函数关系式,解得:
∴过O、D、B三点的抛物线的函数关系式为:.
【解析】【分析】(1)过点D作DE⊥OA于E,可得到:△ADE∽△BAO,根据相似三角形的对应边成比例可求得点D坐标;
(2)根据△ADE∽△BAO,且AE=2,ED=2,可以得到:点B的坐标为B(0,4).设出函数解析式,将O、D、B三点坐标代入即可求出解析式.
8.【答案】解:∵AD=4,DB=8,
∴AB=12,
∵DE∥BC,
∴△ADE∽△ABC,
∴ ,即 ,
∴DE=3.
【解析】【分析】由DE∥BC,判断△ADE∽△ABC,再由相似三角形的性质得出相似比求DE.
9.【答案】解:问题探究:过点C作CE∥AD交BA的延长线于点E, ∴ ,∠BAD=∠E,∠CAD=∠ACE. ∵AD平分∠BAC,∴∠BAD=∠CAD. ∴∠E=∠ACE.∴AC= AE. ∴ . 结论应用:在Rt△ABC中,∠C=90°, . 设CD的长为x,则BD的长为15-x. ∵AD平分∠BAC, ∴ ,即 . 解得 . ∴CD的长为 .
【解析】【分析】 过点C作CE∥AD交BA的延长线于点E,则 ,根据“双平等腰”模型,易证 AC=AE,进而即可得到结论;根据勾股定理,求出AB的长, 设CD的长为x,则BD的长为15-x. 根据角平分线的性质,列出方程,即可求解.
10.【答案】(1)解:如图所示,取格点G、H,连接GH交BC于D,点D即为所求;
∵四边形BGCH是矩形,
∴点D是BC的中点,
∴;
(2)解:如图所示,取格点M、T、H、N,连接MN交AB于P,连接TH交AC于Q,连接PQ,
在线段PQ上任取一点E(不包括端点)即为所求;
由图知,,
∴,
∴∠ABC=90°,
∴,
∵,
∴△MNE∽△PQE,
∴,
∴,
同理可证,
∴,
又∵∠PAQ=∠BAC,
∴△APQ∽△ABC,
∴∠APQ=∠ABC,
∴,
∴.
【解析】【分析】根据要求作出图象即可。
11.【答案】(1)解:点在这个函数的图象上.理由如下:
∵二次函数的图象的顶点坐标为,
∴二次函数的解析式为,
∴当时,.
∴点在这个函数的图象上.
(2)解:∵在中,
∴BC=AD.
∵ED//BC,
∴△EDF∽△CBF,
∴,
又∵,
∴,
∴.
∴.
【解析】【分析】(1)由题意先把顶点坐标代入抛物线的解析式,然后把点(1,-1)代入所求的解析式验证即可判断求解;
(2)由平行四边形的性质可得BC=AD,根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得△EDF∽△CBF,于是可得比例式并结合已知即可求解.
12.【答案】(1)AE= BF
(2)解:上述结成立,理由如下:
连接CE,如图2所示:
∵∠FCE=∠BCA=45°,
∴∠BCF=∠ACE=45°﹣∠ACF,
在Rt△CEF和Rt△CBA中,CE= CF,CA= CB,
∴ = ,
∴△ACE∽△BCF,
∴ = ,
∴AE= BF;
(3)解:如图3﹣1中,当点F落在AC上时,
∵AB=CB=4,∠B=90°,
∴AC= AB=4 ,
∵CF=EF= ,
∴AF=3 ,
∵∠AFE=90°,
∴AE= .
如图3﹣2中,当点F落在AC的延长线上时,同法可得AE= .
综上所述,AE的长为2 或2 .
故答案为:2 或2 .
【解析】【解答】解:(1)结论:AE= BF,理由如下:
∵四边形ABCD和四边形CFEG是正方形,
∴∠B=∠CFE=90°,∠FCE=∠BCA=45°,CE= CF,CE⊥GF,
∴AB∥EF,
∴ = ,
∴AE= BF;
故答案为:AE= BF;
【分析】(1)根据正方形的性质可得∠B=∠CFE=90°,∠FCE=∠BCA=45°,CE=CF,CE⊥GF,则AB∥EF,然后根据平行线分线段成比例的性质进行解答;
(2)连接CE,根据角的和差关系可得∠BCF=∠ACE,易得=,证明△ACE∽△BCF,然后根据相似三角形的性质进行解答;
(3)当点F落在AC上时,由勾股定理可得AC=AB=4,则AF=AC-CF=3,然后利用勾股定理就可求出AE的值;当点F落在AC的延长线上时,同法可得AE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
27.2.2 相似三角形的性质一课一练
一、单选题
1.如图,△ABC∽△ADE , 则下列比例式正确的是( )
A. B. C. D.
2.两个相似三角形的相似比为1:2,则它们面积的比为( )
A.1:4 B.1:2 C.1: D.4:1
3.若△ABC∽△A′B′C′且 = ,△ABC的周长为15cm,则△A′B′C′的周长为( )cm.
A.18 B.20 C. D.
4.△ABC与△A'B'C'是位似图形,且△ABC与△A'B'C'位似比是1:2,已知△ABC的面积是10,则△A'B'C'的面积是( )
A.10 B.20 C.40 D.80
二、填空题
5.若两个相似三角形的相似比为3∶4,则它们的面积比为 .
6.如图,在四边形 中, 于点 , ,且 ,当 , 时,线段 的长度为 .
三、计算题
7.如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.
(1)求点D的坐标;
(2)求经过O、D、B三点的抛物线的函数关系式.
四、解答题
8.如图,在 中,已知 , , , ,求DE的长.
9.问题探究:三角形的角平分线是初中几何中一条非常重要的线段,它除了具有平分角、角平分线上的点到角两边的距离相等这些性质外,还具有以下的性质:
如图①,在△ABC中,AD平分∠BAC交BC于点D,则 。
提示:过点C作CE∥AD交BA的延长线于点E。
请根据上面的提示,写出得到“ “这一结论完整的证明过程。
结论应用:如图②2,在Rt△ABC中,∠C=90°,AC=8,BC=15,AD平分∠BAC交BC于点D。请直接利用“问题探究”的结论,求线段CD的长。
五、作图题
10.图,点A,B,C是的网格上的格点,连接点A,B,C得△ABC,请分别在下列图中使用无刻度的直尺按要求画图.(画图时保留画图痕迹)
(1)在图①中,在BC上找一点D,使;
(2)在图②中,在△ABC内部(不含边界)找一点E,使
六、综合题
11.
(1)已知二次函数的图象的顶点坐标为.判断点是否在这个函数的图象上?为什么?
(2)如图,在中,已知点E在DA的延长线上,,连接CE交BD于点F,求的值.
七、实践探究题
12.如图1所示,边长为4的正方形ABCD与边长为a(0<a<4)的正方形CFEG的顶点C重合,点B在对角线AC上.
(1)[问题发现]如图1所示,AE与BF的数量关系为 ;
(2)[类比探究]如图2所示,将正方形CFEG绕点C旋转,旋转角为α(0<α<30°),请问此时上述结论是否还成立?若成立,写出推理过程,若不成立,说明理由;
(3)[拓展延伸]当a=时,正方形CFEG若按图1所示位置开始旋转,在正方形CFEG的旋转过程中,当点A、F、C在一条直线上时,求出此时线段AE的长.
答案解析部分
1.【答案】D
【解析】【解答】∵△ABC∽△ADE , ∴ ,
故答案为:D.
【分析】本题考查相似三角形的性质,掌握相似三角形的对应边成比例这一性质是解答此题的关键.
2.【答案】A
【解析】【解答】∵两个相似三角形的相似比为1:2,
∴它们面积的比等于: .
故答案为:A.
【分析】根据相似三角形的性质“相似三角形的面积的比等于相似比的平方”可求解.
3.【答案】B
【解析】【解答】∵△ABC∽△A′B′C′,
∴ = =
∴ = = ,
∵△ABC的周长为15cm,
∴△A′B′C′的周长为20cm.
故选B.
【分析】根据比例的等比性质可得相似三角形周长的比等于相似比,可得 = = ,由△ABC的周长为15cm,即可求得△A′B′C′的周长.
4.【答案】A
【解析】【解答】解:∵两个三嘉兴的位似比为1:2
∴两个三角形的为1:4
∵△ABC的面积为10
∴△A'B'C'面积为20
故答案为:B.
【分析】根据相似三角形的性质,计算得到答案即可。
5.【答案】9:16
【解析】【解答】解:∵两个相似五边形的相似比为3:4,
∴它们的面积比为9:16
故答案为9:16
【分析】相似多边形的面积比等于相似比的平方,据此解答即可.
6.【答案】
【解析】【解答】解:如图,在
上截取
,过
作
交
于点
,把
绕
逆时针旋转得
,连接
,
则
,
,
,
∴ ,
又∵ 于点
,
,
,
∴ ,
∴ ,
又∵ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
又
,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴在
中,由勾股定理得,
,
∴ .
故答案为:
.
【分析】在
上截取
,过
作
交
于点
,把
绕
逆时针旋转得
,连接
,易求
,然后证明
,可得
,再证
可得
,由
可得
,从而求出MN=
,证得
,可求出
,在
中,由勾股定理求出CE,利用
即可求解.
7.【答案】(1)如图,过点D作DE⊥OA于E,
在△AED与△BAO中
∵∠EDA+∠EAD=∠EAD+∠BAO=90°,
∴∠EDA=∠BAO,
∵∠AED=∠AOB=90°,
∴△ADE∽△BAO,
∴
∵点A(0,4),DM=6,
∴AO=4,AE=EO-AO=DM-AO=2,
∴ED=,
∴点D的坐标为D(2,6).
(2)∵AE=2,ED=2,△ADE∽△BAO,
∴BO=AO=4
∴点B的坐标为B(4,0)
设:过O、D、B三点的抛物线的函数关系式为:
将O(0,0),B(0,4),D(2,6)代入函数关系式,解得:
∴过O、D、B三点的抛物线的函数关系式为:.
【解析】【分析】(1)过点D作DE⊥OA于E,可得到:△ADE∽△BAO,根据相似三角形的对应边成比例可求得点D坐标;
(2)根据△ADE∽△BAO,且AE=2,ED=2,可以得到:点B的坐标为B(0,4).设出函数解析式,将O、D、B三点坐标代入即可求出解析式.
8.【答案】解:∵AD=4,DB=8,
∴AB=12,
∵DE∥BC,
∴△ADE∽△ABC,
∴ ,即 ,
∴DE=3.
【解析】【分析】由DE∥BC,判断△ADE∽△ABC,再由相似三角形的性质得出相似比求DE.
9.【答案】解:问题探究:过点C作CE∥AD交BA的延长线于点E, ∴ ,∠BAD=∠E,∠CAD=∠ACE. ∵AD平分∠BAC,∴∠BAD=∠CAD. ∴∠E=∠ACE.∴AC= AE. ∴ . 结论应用:在Rt△ABC中,∠C=90°, . 设CD的长为x,则BD的长为15-x. ∵AD平分∠BAC, ∴ ,即 . 解得 . ∴CD的长为 .
【解析】【分析】 过点C作CE∥AD交BA的延长线于点E,则 ,根据“双平等腰”模型,易证 AC=AE,进而即可得到结论;根据勾股定理,求出AB的长, 设CD的长为x,则BD的长为15-x. 根据角平分线的性质,列出方程,即可求解.
10.【答案】(1)解:如图所示,取格点G、H,连接GH交BC于D,点D即为所求;
∵四边形BGCH是矩形,
∴点D是BC的中点,
∴;
(2)解:如图所示,取格点M、T、H、N,连接MN交AB于P,连接TH交AC于Q,连接PQ,
在线段PQ上任取一点E(不包括端点)即为所求;
由图知,,
∴,
∴∠ABC=90°,
∴,
∵,
∴△MNE∽△PQE,
∴,
∴,
同理可证,
∴,
又∵∠PAQ=∠BAC,
∴△APQ∽△ABC,
∴∠APQ=∠ABC,
∴,
∴.
【解析】【分析】根据要求作出图象即可。
11.【答案】(1)解:点在这个函数的图象上.理由如下:
∵二次函数的图象的顶点坐标为,
∴二次函数的解析式为,
∴当时,.
∴点在这个函数的图象上.
(2)解:∵在中,
∴BC=AD.
∵ED//BC,
∴△EDF∽△CBF,
∴,
又∵,
∴,
∴.
∴.
【解析】【分析】(1)由题意先把顶点坐标代入抛物线的解析式,然后把点(1,-1)代入所求的解析式验证即可判断求解;
(2)由平行四边形的性质可得BC=AD,根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得△EDF∽△CBF,于是可得比例式并结合已知即可求解.
12.【答案】(1)AE= BF
(2)解:上述结成立,理由如下:
连接CE,如图2所示:
∵∠FCE=∠BCA=45°,
∴∠BCF=∠ACE=45°﹣∠ACF,
在Rt△CEF和Rt△CBA中,CE= CF,CA= CB,
∴ = ,
∴△ACE∽△BCF,
∴ = ,
∴AE= BF;
(3)解:如图3﹣1中,当点F落在AC上时,
∵AB=CB=4,∠B=90°,
∴AC= AB=4 ,
∵CF=EF= ,
∴AF=3 ,
∵∠AFE=90°,
∴AE= .
如图3﹣2中,当点F落在AC的延长线上时,同法可得AE= .
综上所述,AE的长为2 或2 .
故答案为:2 或2 .
【解析】【解答】解:(1)结论:AE= BF,理由如下:
∵四边形ABCD和四边形CFEG是正方形,
∴∠B=∠CFE=90°,∠FCE=∠BCA=45°,CE= CF,CE⊥GF,
∴AB∥EF,
∴ = ,
∴AE= BF;
故答案为:AE= BF;
【分析】(1)根据正方形的性质可得∠B=∠CFE=90°,∠FCE=∠BCA=45°,CE=CF,CE⊥GF,则AB∥EF,然后根据平行线分线段成比例的性质进行解答;
(2)连接CE,根据角的和差关系可得∠BCF=∠ACE,易得=,证明△ACE∽△BCF,然后根据相似三角形的性质进行解答;
(3)当点F落在AC上时,由勾股定理可得AC=AB=4,则AF=AC-CF=3,然后利用勾股定理就可求出AE的值;当点F落在AC的延长线上时,同法可得AE.
27.2.2 相似三角形的性质一课一练
一、单选题
1.如图,△ABC∽△ADE , 则下列比例式正确的是( )
A. B. C. D.
2.两个相似三角形的相似比为1:2,则它们面积的比为( )
A.1:4 B.1:2 C.1: D.4:1
3.若△ABC∽△A′B′C′且 = ,△ABC的周长为15cm,则△A′B′C′的周长为( )cm.
A.18 B.20 C. D.
4.△ABC与△A'B'C'是位似图形,且△ABC与△A'B'C'位似比是1:2,已知△ABC的面积是10,则△A'B'C'的面积是( )
A.10 B.20 C.40 D.80
二、填空题
5.若两个相似三角形的相似比为3∶4,则它们的面积比为 .
6.如图,在四边形 中, 于点 , ,且 ,当 , 时,线段 的长度为 .
三、计算题
7.如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.
(1)求点D的坐标;
(2)求经过O、D、B三点的抛物线的函数关系式.
四、解答题
8.如图,在 中,已知 , , , ,求DE的长.
9.问题探究:三角形的角平分线是初中几何中一条非常重要的线段,它除了具有平分角、角平分线上的点到角两边的距离相等这些性质外,还具有以下的性质:
如图①,在△ABC中,AD平分∠BAC交BC于点D,则 。
提示:过点C作CE∥AD交BA的延长线于点E。
请根据上面的提示,写出得到“ “这一结论完整的证明过程。
结论应用:如图②2,在Rt△ABC中,∠C=90°,AC=8,BC=15,AD平分∠BAC交BC于点D。请直接利用“问题探究”的结论,求线段CD的长。
五、作图题
10.图,点A,B,C是的网格上的格点,连接点A,B,C得△ABC,请分别在下列图中使用无刻度的直尺按要求画图.(画图时保留画图痕迹)
(1)在图①中,在BC上找一点D,使;
(2)在图②中,在△ABC内部(不含边界)找一点E,使
六、综合题
11.
(1)已知二次函数的图象的顶点坐标为.判断点是否在这个函数的图象上?为什么?
(2)如图,在中,已知点E在DA的延长线上,,连接CE交BD于点F,求的值.
七、实践探究题
12.如图1所示,边长为4的正方形ABCD与边长为a(0<a<4)的正方形CFEG的顶点C重合,点B在对角线AC上.
(1)[问题发现]如图1所示,AE与BF的数量关系为 ;
(2)[类比探究]如图2所示,将正方形CFEG绕点C旋转,旋转角为α(0<α<30°),请问此时上述结论是否还成立?若成立,写出推理过程,若不成立,说明理由;
(3)[拓展延伸]当a=时,正方形CFEG若按图1所示位置开始旋转,在正方形CFEG的旋转过程中,当点A、F、C在一条直线上时,求出此时线段AE的长.
答案解析部分
1.【答案】D
【解析】【解答】∵△ABC∽△ADE , ∴ ,
故答案为:D.
【分析】本题考查相似三角形的性质,掌握相似三角形的对应边成比例这一性质是解答此题的关键.
2.【答案】A
【解析】【解答】∵两个相似三角形的相似比为1:2,
∴它们面积的比等于: .
故答案为:A.
【分析】根据相似三角形的性质“相似三角形的面积的比等于相似比的平方”可求解.
3.【答案】B
【解析】【解答】∵△ABC∽△A′B′C′,
∴ = =
∴ = = ,
∵△ABC的周长为15cm,
∴△A′B′C′的周长为20cm.
故选B.
【分析】根据比例的等比性质可得相似三角形周长的比等于相似比,可得 = = ,由△ABC的周长为15cm,即可求得△A′B′C′的周长.
4.【答案】A
【解析】【解答】解:∵两个三嘉兴的位似比为1:2
∴两个三角形的为1:4
∵△ABC的面积为10
∴△A'B'C'面积为20
故答案为:B.
【分析】根据相似三角形的性质,计算得到答案即可。
5.【答案】9:16
【解析】【解答】解:∵两个相似五边形的相似比为3:4,
∴它们的面积比为9:16
故答案为9:16
【分析】相似多边形的面积比等于相似比的平方,据此解答即可.
6.【答案】
【解析】【解答】解:如图,在
上截取
,过
作
交
于点
,把
绕
逆时针旋转得
,连接
,
则
,
,
,
∴ ,
又∵ 于点
,
,
,
∴ ,
∴ ,
又∵ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
又
,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴在
中,由勾股定理得,
,
∴ .
故答案为:
.
【分析】在
上截取
,过
作
交
于点
,把
绕
逆时针旋转得
,连接
,易求
,然后证明
,可得
,再证
可得
,由
可得
,从而求出MN=
,证得
,可求出
,在
中,由勾股定理求出CE,利用
即可求解.
7.【答案】(1)如图,过点D作DE⊥OA于E,
在△AED与△BAO中
∵∠EDA+∠EAD=∠EAD+∠BAO=90°,
∴∠EDA=∠BAO,
∵∠AED=∠AOB=90°,
∴△ADE∽△BAO,
∴
∵点A(0,4),DM=6,
∴AO=4,AE=EO-AO=DM-AO=2,
∴ED=,
∴点D的坐标为D(2,6).
(2)∵AE=2,ED=2,△ADE∽△BAO,
∴BO=AO=4
∴点B的坐标为B(4,0)
设:过O、D、B三点的抛物线的函数关系式为:
将O(0,0),B(0,4),D(2,6)代入函数关系式,解得:
∴过O、D、B三点的抛物线的函数关系式为:.
【解析】【分析】(1)过点D作DE⊥OA于E,可得到:△ADE∽△BAO,根据相似三角形的对应边成比例可求得点D坐标;
(2)根据△ADE∽△BAO,且AE=2,ED=2,可以得到:点B的坐标为B(0,4).设出函数解析式,将O、D、B三点坐标代入即可求出解析式.
8.【答案】解:∵AD=4,DB=8,
∴AB=12,
∵DE∥BC,
∴△ADE∽△ABC,
∴ ,即 ,
∴DE=3.
【解析】【分析】由DE∥BC,判断△ADE∽△ABC,再由相似三角形的性质得出相似比求DE.
9.【答案】解:问题探究:过点C作CE∥AD交BA的延长线于点E, ∴ ,∠BAD=∠E,∠CAD=∠ACE. ∵AD平分∠BAC,∴∠BAD=∠CAD. ∴∠E=∠ACE.∴AC= AE. ∴ . 结论应用:在Rt△ABC中,∠C=90°, . 设CD的长为x,则BD的长为15-x. ∵AD平分∠BAC, ∴ ,即 . 解得 . ∴CD的长为 .
【解析】【分析】 过点C作CE∥AD交BA的延长线于点E,则 ,根据“双平等腰”模型,易证 AC=AE,进而即可得到结论;根据勾股定理,求出AB的长, 设CD的长为x,则BD的长为15-x. 根据角平分线的性质,列出方程,即可求解.
10.【答案】(1)解:如图所示,取格点G、H,连接GH交BC于D,点D即为所求;
∵四边形BGCH是矩形,
∴点D是BC的中点,
∴;
(2)解:如图所示,取格点M、T、H、N,连接MN交AB于P,连接TH交AC于Q,连接PQ,
在线段PQ上任取一点E(不包括端点)即为所求;
由图知,,
∴,
∴∠ABC=90°,
∴,
∵,
∴△MNE∽△PQE,
∴,
∴,
同理可证,
∴,
又∵∠PAQ=∠BAC,
∴△APQ∽△ABC,
∴∠APQ=∠ABC,
∴,
∴.
【解析】【分析】根据要求作出图象即可。
11.【答案】(1)解:点在这个函数的图象上.理由如下:
∵二次函数的图象的顶点坐标为,
∴二次函数的解析式为,
∴当时,.
∴点在这个函数的图象上.
(2)解:∵在中,
∴BC=AD.
∵ED//BC,
∴△EDF∽△CBF,
∴,
又∵,
∴,
∴.
∴.
【解析】【分析】(1)由题意先把顶点坐标代入抛物线的解析式,然后把点(1,-1)代入所求的解析式验证即可判断求解;
(2)由平行四边形的性质可得BC=AD,根据“平行与三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似”可得△EDF∽△CBF,于是可得比例式并结合已知即可求解.
12.【答案】(1)AE= BF
(2)解:上述结成立,理由如下:
连接CE,如图2所示:
∵∠FCE=∠BCA=45°,
∴∠BCF=∠ACE=45°﹣∠ACF,
在Rt△CEF和Rt△CBA中,CE= CF,CA= CB,
∴ = ,
∴△ACE∽△BCF,
∴ = ,
∴AE= BF;
(3)解:如图3﹣1中,当点F落在AC上时,
∵AB=CB=4,∠B=90°,
∴AC= AB=4 ,
∵CF=EF= ,
∴AF=3 ,
∵∠AFE=90°,
∴AE= .
如图3﹣2中,当点F落在AC的延长线上时,同法可得AE= .
综上所述,AE的长为2 或2 .
故答案为:2 或2 .
【解析】【解答】解:(1)结论:AE= BF,理由如下:
∵四边形ABCD和四边形CFEG是正方形,
∴∠B=∠CFE=90°,∠FCE=∠BCA=45°,CE= CF,CE⊥GF,
∴AB∥EF,
∴ = ,
∴AE= BF;
故答案为:AE= BF;
【分析】(1)根据正方形的性质可得∠B=∠CFE=90°,∠FCE=∠BCA=45°,CE=CF,CE⊥GF,则AB∥EF,然后根据平行线分线段成比例的性质进行解答;
(2)连接CE,根据角的和差关系可得∠BCF=∠ACE,易得=,证明△ACE∽△BCF,然后根据相似三角形的性质进行解答;
(3)当点F落在AC上时,由勾股定理可得AC=AB=4,则AF=AC-CF=3,然后利用勾股定理就可求出AE的值;当点F落在AC的延长线上时,同法可得AE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
