27.2.3 相似三角形应用举例一课一练(含解析)
文档属性
| 名称 | 27.2.3 相似三角形应用举例一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 395.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
27.2.3 相似三角形应用举例一课一练
一、单选题
1.某班某同学要测量学校升旗的旗杆高度,在同一时刻,量得某一同学的身高是1.5m,影长是1m,旗杆的影长是8m,则旗杆的高度是( )
A.12m B.11m C.10m D.9m
2.如图,在 ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
3.如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,AB:AC=1:9,则建筑物CD的高是( )
A.9.6m B.10.8m C.12m D.14m
4.某一时刻,身高1.6m 的小明在阳光下的影长是0.4m.同一时刻同一地点,测得某旗杆的影长是5m,则该旗杆的高度是()
A.1.25m B.10m C.20m D.8m
5.一个钢筋三角架三边长分别为20cm,50cm,60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有( ).
A.一种 B.两种 C.三种 D.四种
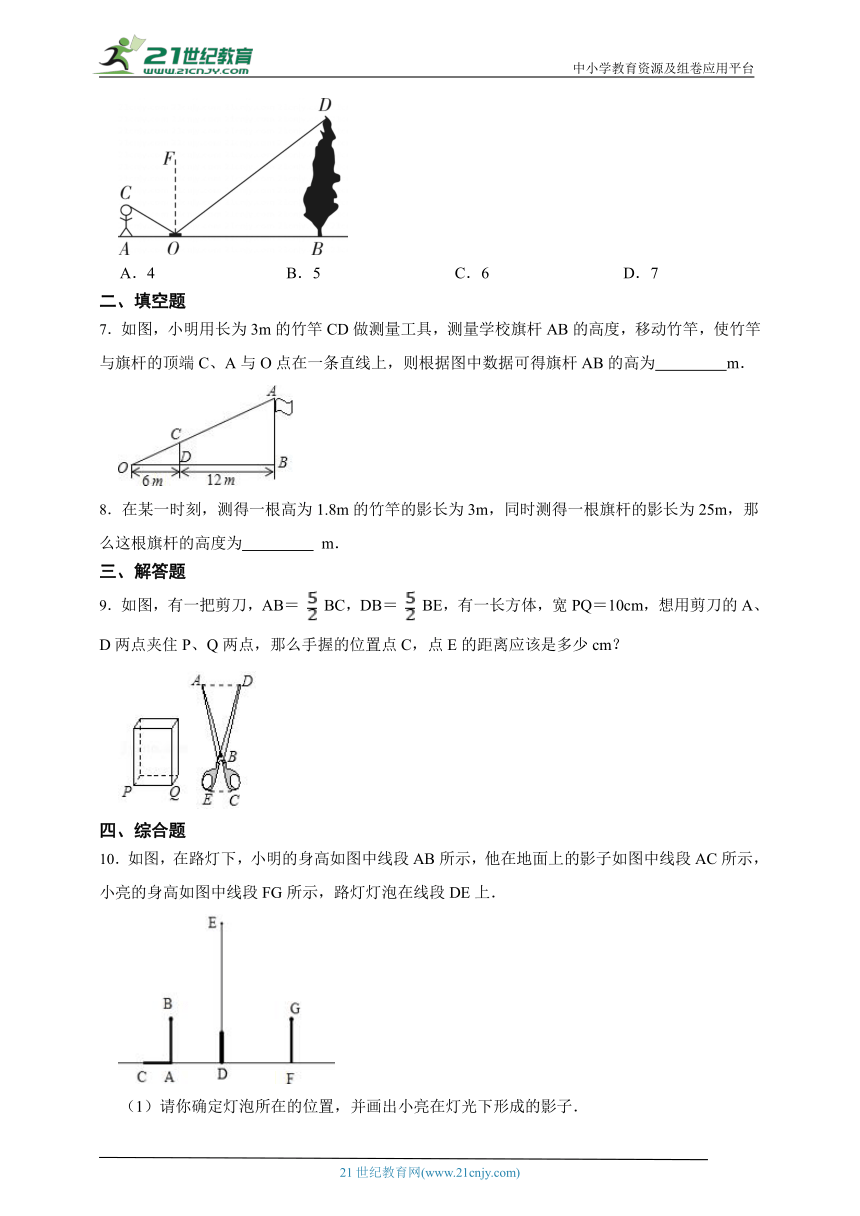
6.如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点,镜子,树底三点在同一水平线上,眼睛与地面的高度为1.6米,米,米,则树高为( )米
A.4 B.5 C.6 D.7
二、填空题
7.如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为 m.
8.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为 m.
三、解答题
9.如图,有一把剪刀,AB= BC,DB= BE,有一长方体,宽PQ=10cm,想用剪刀的A、D两点夹住P、Q两点,那么手握的位置点C,点E的距离应该是多少cm?
四、综合题
10.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
11.在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
12.为了测量一棵大树的高度,准备了如下测量工具:①镜子;②皮尺;③长为2m的标杆;④高为1.5m的测角仪(能测量仰角和俯角的仪器),请根据你所设计的测量方案,回答下列问题:
(1)在你设计的方案上,选用的测量工具是 ;
(2)在下图中画出你的测量方案示意图;
(3)你需要测量示意图中的哪些数据,并用a,b,c,α等字母表示测得的数据;
(4)写出求树高的算式:AB= m.
答案解析部分
1.【答案】A
【解析】【分析】因为在同一时刻同一地点任何物体的高与其影子长比值是相同的,所以同学的身高与其影子长的比值等于旗杆的高与其影子长的比值.
【解答】设旗杆的高度为x,
根据在同一时刻同一地点任何物体的高与其影子长比值是相同的,得:,
∴
∴旗杆的高度是12m.
故选A.
2.【答案】C
【解析】【解答】解:∵在 ABCD中,E为CD中点,
∴AB=CD=2DE,
又∵AB∥CD,
∴△AOB∽△EOD,
∴ =( )2=4,
∴S△AOB=4S△DOE=48cm2.
故答案为:C.
【分析】由平行四边形可得△AOB∽△EOD,由面积比等于相似比的平方,可得面积之比,依此可求得S△AOB。
3.【答案】B
【解析】【解答】解:∵EB∥CD,
∴△ABE∽△ACD,
∴ ,即 ,
∴CD=10.8(米).
故答案为:B.
【分析】利用EB∥CD可证得△ABE∽△ACD,利用相似三角形的对应边成比例,可得比列式,即可求出CD的长.
4.【答案】C
【解析】【分析】设该旗杆的高度为xm,根据三角形相似的性质得到同一时刻同一地点物体的高度与其影长的比相等,即有1.6:0.4=x:5,然后解方程即可.
【解答】设该旗杆的高度为xm,根据题意得,1.6:0.4=x:5,
解得x=20(m).
即该旗杆的高度是20m.
故选C.
【点评】本题考查了三角形相似的性质:相似三角形对应边的比相等
5.【答案】B
【解析】【解答】取30cm为一边,另两边设为xcm、ycm;
( 1 )30cm与20cm对应,即 ,
解得x=75,y=90;
75+90>50,不可以.
( 2 )30cm与50cm对应,即 ,
解得x=12,y=36;
12+36=48<50,可以.
( 3 )30cm与60cm对应,即 ,
解得x=10,y=25;
10+25<50,可以.
所以有两种不同的截法.
故答案为:B.
【分析】根据相似三角形对应边成比例,分三种情况列方程解答.舍去不合题意的情况.
6.【答案】A
【解析】【解答】解:由题意得
∠COF=∠DOF,∠ACO=90°-∠COF,∠BOD=90°-∠DOF,
∴∠ACO=∠BOD,
∵∠OAC=∠OBD=90°,
∴△ACO∽△BDO,
∴即
解之:BD=4.
故答案为:A
【分析】利用已知条件和余角的性质可证得∠ACO=∠BOD,利用有两组对应角分别相等的两三角形相似,可证得△ACO∽△BDO,利用相似三角形的对应边成比例,可求出BD的长.
7.【答案】9
【解析】【解答】由得到,,即,∴AB=9,故本题答案为9
【分析】本题主要考查相似三角形的应用,属于简单题.
8.【答案】15
【解析】【解答】解:设旗杆高度为x米,
由题意得, ,
解得x=15.
故答案为:15.
【分析】根据同时同地物高与影长成正比列式计算即可得解.
9.【答案】解:∵AB=2.5BC,DB=2.5BE,
∴ ,
又∵∠ABD=∠CBE,
∴△ABD∽△CBE,
∴ = = ,
则 = ,
解得:EC=4,
答:点C,点E的距离应该是4cm.
【解析】【分析】根据题意得出△ABD和△CBD的两条边对应成比例,结合对顶角相等,证明 △ABD∽△CBE, 则可列出比例式代值计算即可.
10.【答案】(1)解:如图,点O为灯泡所在的位置,线段FH为小亮在灯光下形成的影子.
(2)解:由已知可得, ,
∴ ,
∴OD=4m,
∴灯泡的高为4m.
【解析】【分析】(1)根据题意画出图形。
(2)利用平行线分线段成比例,得出对应线段成比例,求出OD的长。
11.【答案】(1)解:∵点D关于直线AE的对称点为F,
∴∠EAF=∠DAE,AD=AF,
又∵∠BAC=2∠DAE,
∴∠BAC=∠DAF,
∵AB=AC,
∴ ,
∴△ADF∽△ABC
(2)解:∵点D关于直线AE的对称点为F,
∴EF=DE,AF=AD,
∵α=45°,
∴∠BAD=90°﹣∠CAD,
∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD,
∴∠BAD=∠CAF,
在△ABD和△ACF中, ,
∴△ABD≌△ACF(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=2α,α=45°,
∴△ABC是等腰直角三角形,
∴∠B=∠ACB=45°,
∴∠ECF=∠ACB+∠ACF=45°+45°=90°,
在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,
所以,DE2=BD2+CE2
(3)解:DE2=BD2+CE2还能成立.
理由如下:作点D关于AE的对称点F,连接EF、CF,
由轴对称的性质得,EF=DE,AF=AD,
∵α=45°,
∴∠BAD=90°﹣∠CAD,
∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD,
∴∠BAD=∠CAF,
在△ABD和△ACF中, ,
∴△ABD≌△ACF(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=2α,α=45°,
∴△ABC是等腰直角三角形,
∴∠B=∠ACB=45°,
∴∠ECF=∠ACB+∠ACF=45°+45°=90°,
在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,
所以,DE2=BD2+CE2.
【解析】【分析】(1)根据轴对称的性质可得∠EAF=∠DAE,AD=AF,再求出∠BAC=∠DAF,然后根据两边对应成比例,夹角相等两三角形相似证明;
(2)根据轴对称的性质可得EF=DE,AF=AD,再求出∠BAD=∠CAF,然后利用“边角边”证明△ABD和△ACF全等,根据全等三角形对应边相等可得CF=BD,全等三角形对应角相等可得∠ACF=∠B,然后求出∠ECF=90°,最后利用勾股定理证明即可;
(3)作点D关于AE的对称点F,连接EF、CF,根据轴对称的性质可得EF=DE,AF=AD,再根据同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△ABD和△ACF全等,根据全等三角形对应边相等可得CF=BD,全等三角形对应角相等可得∠ACF=∠B,然后求出∠ECF=90°,最后利用勾股定理证明即可.本题是相似形综合题,主要利用了轴对称的性质,相似三角形的判定,同角的余角相等的性质,全等三角形的判定与性质,勾股定理,此类题目,小题间的思路相同是解题的关键.
12.【答案】(1)解:镜子,皮尺
(2)解:测量方案示意图:
(3)解:EA(镜子离树的距离)=a,EC(人离镜子的距离)=b,DC(目高)=c
(4)
【解析】【解答】解:(4)根据相似三角形的性质;可得: = ;即AB= .
故答案为: .
【分析】(1)通过设计方案可选择测量工具;
(2)设计出利用相似形的知识来测量树的高度;
(3)通过相似形的性质写出表达式可表示出树高;
(4)根据相似性的性质即可写出曙光的计算式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
27.2.3 相似三角形应用举例一课一练
一、单选题
1.某班某同学要测量学校升旗的旗杆高度,在同一时刻,量得某一同学的身高是1.5m,影长是1m,旗杆的影长是8m,则旗杆的高度是( )
A.12m B.11m C.10m D.9m
2.如图,在 ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2,则S△AOB等于( )
A.24cm2 B.36cm2 C.48cm2 D.60cm2
3.如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,AB:AC=1:9,则建筑物CD的高是( )
A.9.6m B.10.8m C.12m D.14m
4.某一时刻,身高1.6m 的小明在阳光下的影长是0.4m.同一时刻同一地点,测得某旗杆的影长是5m,则该旗杆的高度是()
A.1.25m B.10m C.20m D.8m
5.一个钢筋三角架三边长分别为20cm,50cm,60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm和50cm的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有( ).
A.一种 B.两种 C.三种 D.四种
6.如图,某同学利用镜面反射的原理巧妙地测出了树的高度,已知人的站位点,镜子,树底三点在同一水平线上,眼睛与地面的高度为1.6米,米,米,则树高为( )米
A.4 B.5 C.6 D.7
二、填空题
7.如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为 m.
8.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为 m.
三、解答题
9.如图,有一把剪刀,AB= BC,DB= BE,有一长方体,宽PQ=10cm,想用剪刀的A、D两点夹住P、Q两点,那么手握的位置点C,点E的距离应该是多少cm?
四、综合题
10.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
11.在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
12.为了测量一棵大树的高度,准备了如下测量工具:①镜子;②皮尺;③长为2m的标杆;④高为1.5m的测角仪(能测量仰角和俯角的仪器),请根据你所设计的测量方案,回答下列问题:
(1)在你设计的方案上,选用的测量工具是 ;
(2)在下图中画出你的测量方案示意图;
(3)你需要测量示意图中的哪些数据,并用a,b,c,α等字母表示测得的数据;
(4)写出求树高的算式:AB= m.
答案解析部分
1.【答案】A
【解析】【分析】因为在同一时刻同一地点任何物体的高与其影子长比值是相同的,所以同学的身高与其影子长的比值等于旗杆的高与其影子长的比值.
【解答】设旗杆的高度为x,
根据在同一时刻同一地点任何物体的高与其影子长比值是相同的,得:,
∴
∴旗杆的高度是12m.
故选A.
2.【答案】C
【解析】【解答】解:∵在 ABCD中,E为CD中点,
∴AB=CD=2DE,
又∵AB∥CD,
∴△AOB∽△EOD,
∴ =( )2=4,
∴S△AOB=4S△DOE=48cm2.
故答案为:C.
【分析】由平行四边形可得△AOB∽△EOD,由面积比等于相似比的平方,可得面积之比,依此可求得S△AOB。
3.【答案】B
【解析】【解答】解:∵EB∥CD,
∴△ABE∽△ACD,
∴ ,即 ,
∴CD=10.8(米).
故答案为:B.
【分析】利用EB∥CD可证得△ABE∽△ACD,利用相似三角形的对应边成比例,可得比列式,即可求出CD的长.
4.【答案】C
【解析】【分析】设该旗杆的高度为xm,根据三角形相似的性质得到同一时刻同一地点物体的高度与其影长的比相等,即有1.6:0.4=x:5,然后解方程即可.
【解答】设该旗杆的高度为xm,根据题意得,1.6:0.4=x:5,
解得x=20(m).
即该旗杆的高度是20m.
故选C.
【点评】本题考查了三角形相似的性质:相似三角形对应边的比相等
5.【答案】B
【解析】【解答】取30cm为一边,另两边设为xcm、ycm;
( 1 )30cm与20cm对应,即 ,
解得x=75,y=90;
75+90>50,不可以.
( 2 )30cm与50cm对应,即 ,
解得x=12,y=36;
12+36=48<50,可以.
( 3 )30cm与60cm对应,即 ,
解得x=10,y=25;
10+25<50,可以.
所以有两种不同的截法.
故答案为:B.
【分析】根据相似三角形对应边成比例,分三种情况列方程解答.舍去不合题意的情况.
6.【答案】A
【解析】【解答】解:由题意得
∠COF=∠DOF,∠ACO=90°-∠COF,∠BOD=90°-∠DOF,
∴∠ACO=∠BOD,
∵∠OAC=∠OBD=90°,
∴△ACO∽△BDO,
∴即
解之:BD=4.
故答案为:A
【分析】利用已知条件和余角的性质可证得∠ACO=∠BOD,利用有两组对应角分别相等的两三角形相似,可证得△ACO∽△BDO,利用相似三角形的对应边成比例,可求出BD的长.
7.【答案】9
【解析】【解答】由得到,,即,∴AB=9,故本题答案为9
【分析】本题主要考查相似三角形的应用,属于简单题.
8.【答案】15
【解析】【解答】解:设旗杆高度为x米,
由题意得, ,
解得x=15.
故答案为:15.
【分析】根据同时同地物高与影长成正比列式计算即可得解.
9.【答案】解:∵AB=2.5BC,DB=2.5BE,
∴ ,
又∵∠ABD=∠CBE,
∴△ABD∽△CBE,
∴ = = ,
则 = ,
解得:EC=4,
答:点C,点E的距离应该是4cm.
【解析】【分析】根据题意得出△ABD和△CBD的两条边对应成比例,结合对顶角相等,证明 △ABD∽△CBE, 则可列出比例式代值计算即可.
10.【答案】(1)解:如图,点O为灯泡所在的位置,线段FH为小亮在灯光下形成的影子.
(2)解:由已知可得, ,
∴ ,
∴OD=4m,
∴灯泡的高为4m.
【解析】【分析】(1)根据题意画出图形。
(2)利用平行线分线段成比例,得出对应线段成比例,求出OD的长。
11.【答案】(1)解:∵点D关于直线AE的对称点为F,
∴∠EAF=∠DAE,AD=AF,
又∵∠BAC=2∠DAE,
∴∠BAC=∠DAF,
∵AB=AC,
∴ ,
∴△ADF∽△ABC
(2)解:∵点D关于直线AE的对称点为F,
∴EF=DE,AF=AD,
∵α=45°,
∴∠BAD=90°﹣∠CAD,
∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD,
∴∠BAD=∠CAF,
在△ABD和△ACF中, ,
∴△ABD≌△ACF(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=2α,α=45°,
∴△ABC是等腰直角三角形,
∴∠B=∠ACB=45°,
∴∠ECF=∠ACB+∠ACF=45°+45°=90°,
在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,
所以,DE2=BD2+CE2
(3)解:DE2=BD2+CE2还能成立.
理由如下:作点D关于AE的对称点F,连接EF、CF,
由轴对称的性质得,EF=DE,AF=AD,
∵α=45°,
∴∠BAD=90°﹣∠CAD,
∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD,
∴∠BAD=∠CAF,
在△ABD和△ACF中, ,
∴△ABD≌△ACF(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=2α,α=45°,
∴△ABC是等腰直角三角形,
∴∠B=∠ACB=45°,
∴∠ECF=∠ACB+∠ACF=45°+45°=90°,
在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,
所以,DE2=BD2+CE2.
【解析】【分析】(1)根据轴对称的性质可得∠EAF=∠DAE,AD=AF,再求出∠BAC=∠DAF,然后根据两边对应成比例,夹角相等两三角形相似证明;
(2)根据轴对称的性质可得EF=DE,AF=AD,再求出∠BAD=∠CAF,然后利用“边角边”证明△ABD和△ACF全等,根据全等三角形对应边相等可得CF=BD,全等三角形对应角相等可得∠ACF=∠B,然后求出∠ECF=90°,最后利用勾股定理证明即可;
(3)作点D关于AE的对称点F,连接EF、CF,根据轴对称的性质可得EF=DE,AF=AD,再根据同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△ABD和△ACF全等,根据全等三角形对应边相等可得CF=BD,全等三角形对应角相等可得∠ACF=∠B,然后求出∠ECF=90°,最后利用勾股定理证明即可.本题是相似形综合题,主要利用了轴对称的性质,相似三角形的判定,同角的余角相等的性质,全等三角形的判定与性质,勾股定理,此类题目,小题间的思路相同是解题的关键.
12.【答案】(1)解:镜子,皮尺
(2)解:测量方案示意图:
(3)解:EA(镜子离树的距离)=a,EC(人离镜子的距离)=b,DC(目高)=c
(4)
【解析】【解答】解:(4)根据相似三角形的性质;可得: = ;即AB= .
故答案为: .
【分析】(1)通过设计方案可选择测量工具;
(2)设计出利用相似形的知识来测量树的高度;
(3)通过相似形的性质写出表达式可表示出树高;
(4)根据相似性的性质即可写出曙光的计算式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
