28.2 解直角三角形及其应用一课一练(含解析)
文档属性
| 名称 | 28.2 解直角三角形及其应用一课一练(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 756.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-06 22:58:27 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
28.2 解直角三角形及其应用一课一练
一、单选题
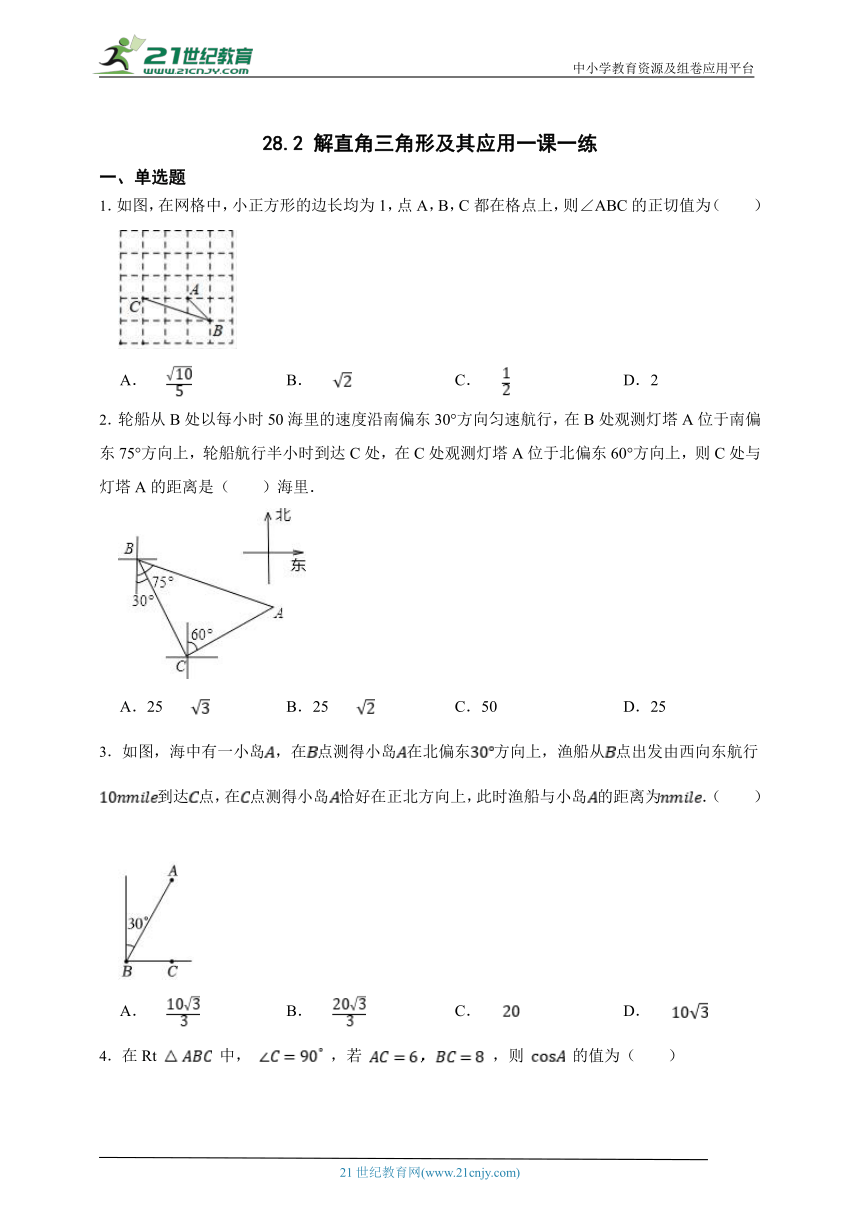
1.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值为( )
A. B. C. D.2
2.轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
A.25 B.25 C.50 D.25
3.如图,海中有一小岛,在点测得小岛在北偏东方向上,渔船从点出发由西向东航行到达点,在点测得小岛恰好在正北方向上,此时渔船与小岛的距离为.( )
A. B. C. D.
4.在Rt 中, ,若 ,则 的值为( )
A. B. C. D.
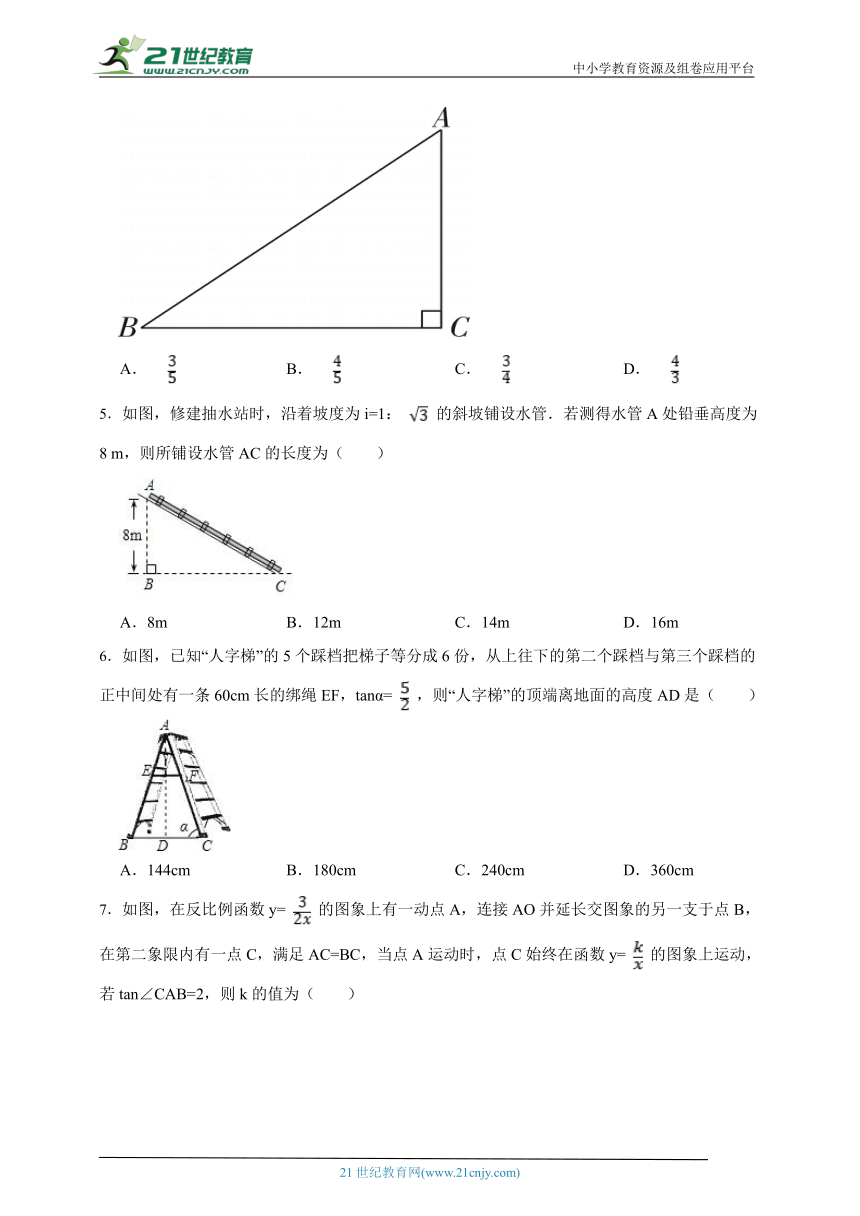
5.如图,修建抽水站时,沿着坡度为i=1: 的斜坡铺设水管.若测得水管A处铅垂高度为8 m,则所铺设水管AC的长度为( )
A.8m B.12m C.14m D.16m
6.如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα= ,则“人字梯”的顶端离地面的高度AD是( )
A.144cm B.180cm C.240cm D.360cm
7.如图,在反比例函数y= 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= 的图象上运动,若tan∠CAB=2,则k的值为( )
A.﹣3 B.﹣6 C.﹣9 D.﹣12
二、填空题
8.某人沿着坡度为 的坡面前进了 米,此时他与水平地面的垂直距离为 米.
9.在中,,是高,且,则 .
三、解答题
10.如图1是“东方之星”救援打捞现场图,小红据此构造出一个如图2所示的数学模型,已知:A、B、D三点在同一水平线上,CD⊥AD,∠A=30°,∠CBD=75°,AB=60m.
(1)求点B到AC的距离;
(2)求线段CD的长度.
四、综合题
11.已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且cot∠ACB=
求:
(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值.
五、实践探究题
12.如图
(1)问题提出
如图,△ABC为等边三角形,边长为6cm,动点M从点B出发,沿着三角形的三条边顺时针方向以2cm/s的速度运动,动点N从点C出发,沿着三角形的三条边逆时针方向以1cm/s的速度运动.动点M、N同时出发,当点M在AB上运动且MN⊥AB时,求点M运动的时间.
(2)问题解决
某小区有一个边长为4米的等边三角形花坛,六一将至,物业借助花坛△ABC举办了一个有奖活动,一家四口举着一根长绳在花坛三边任选位置站立(不能站在各边中点上),四人拉紧、拉直长绳后(长绳可有剩余)可得到一个四边形,如工作人员量得这个四边形是平行四边形,则可领取奖品一份.笑笑和爸爸、妈妈、奶奶一起参加活动,四人的方案是奶奶在A点站立不动,妈妈在△ABC边上某点D处站立不动,爸爸从点B出发,沿着花坛顺时针方向以2米/秒的速度走动(可看作花坛边上运动的点M),同时笑笑从点C出发,沿着花坛逆时针方向以1米/秒的速度走动(可看作花坛边上运动的点N).若笑笑出发不到6秒,一家人就得奖了,那么妈妈所选的位置D距点C多少米?
答案解析部分
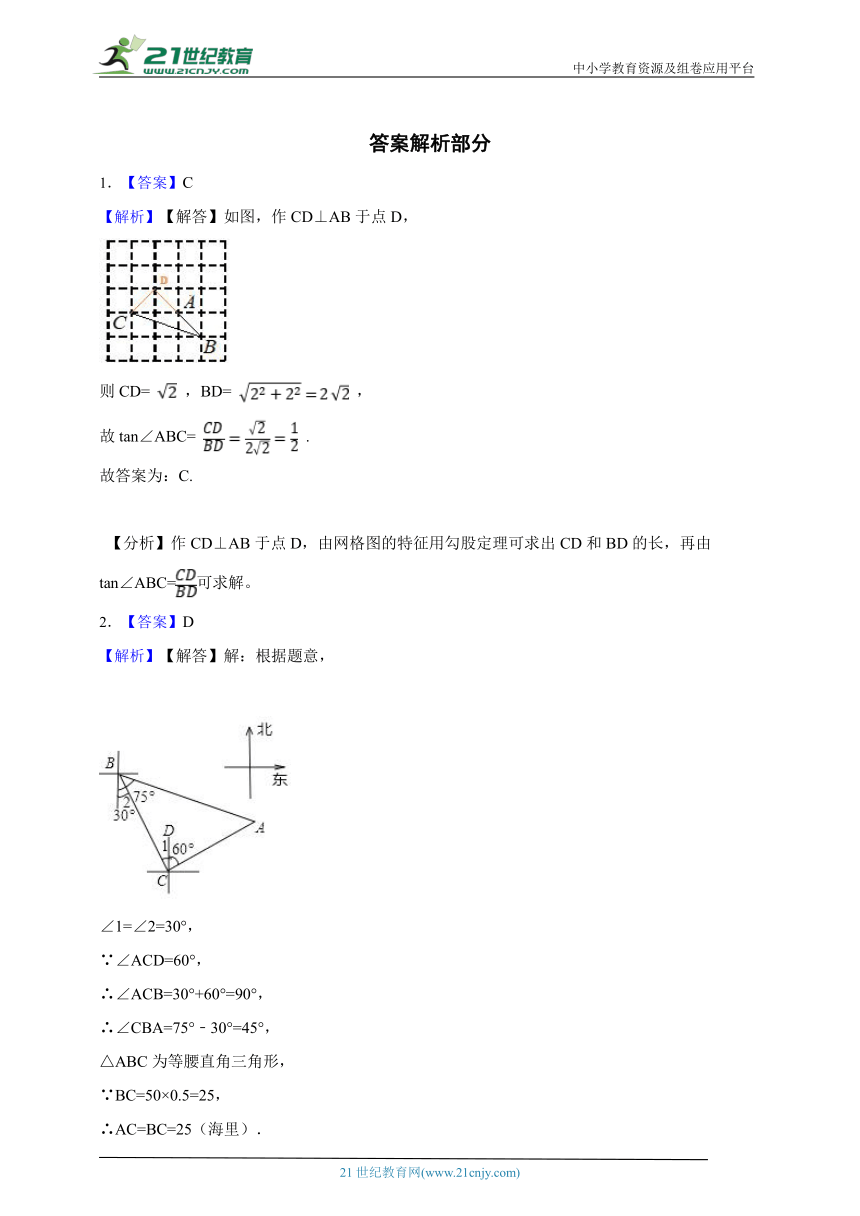
1.【答案】C
【解析】【解答】如图,作CD⊥AB于点D,
则CD= ,BD= ,
故tan∠ABC= .
故答案为:C.
【分析】作CD⊥AB于点D,由网格图的特征用勾股定理可求出CD和BD的长,再由tan∠ABC=可求解。
2.【答案】D
【解析】【解答】解:根据题意,
∠1=∠2=30°,
∵∠ACD=60°,
∴∠ACB=30°+60°=90°,
∴∠CBA=75°﹣30°=45°,
△ABC为等腰直角三角形,
∵BC=50×0.5=25,
∴AC=BC=25(海里).
故答案为:D.
【分析】根据题意推出△ABC为等腰直角三角形,然后根据路程等于速度乘以时间算出BC的长,进而根据等腰三角形的性质得出AC的长。
3.【答案】D
【解析】【解答】解:如图,连接AC,
由题意得∠ACB=90°,∠ABC=60°,BC=10nmile,
∴AC=BC×tan∠ABC=10×tan60°=10×=10nmile.
故答案为:D.
【分析】连接AC根据∠ABC的正切函数可得AC=BC×tan∠ABC,从而代值计算可得答案.
4.【答案】A
【解析】【解答】解:∵∠C=90°,
∴AB==10,
∴cosA===.
故答案为:A.
【分析】根据勾股定理先求出AB长,然后根据余弦三角函数的定义计算即可.
5.【答案】D
【解析】【解答】解;∵该斜坡的坡度为i=1: ,
∴AB:BC=1: ,
∵AB=8m,
∴BC=8 m,
则AC= m.
故答案为:D.
【分析】利用解直角三角形的坡度问题进行求解即可。
6.【答案】B
【解析】【解答】解:如图:
根据题意可知:△AFO∽△ACD,OF= EF=30cm
∴ ,
∴
∴CD=72cm,
∵tanα=
∴
∴AD= =180cm.
故选:B.
【分析】根据题意可知:△AEO∽△ABD,从而可求得BD的长,然后根据锐角三角函数的定义可求得AD的长.
7.【答案】B
【解析】【解答】解:如图,连接OC,过点A作AE⊥y轴于点E,过点C作CF⊥y轴于点F,
∵由直线AB与反比例函数y= 的对称性可知A、B点关于O点对称,
∴AO=BO.
又∵AC=BC,
∴CO⊥AB.
∵∠AOE+∠AOF=90°,∠AOF+∠COF=90°,
∴∠AOE=∠COF,
又∵∠AEO=90°,∠CFO=90°,
∴△AOE∽△COF,
∴ = = ,
∵tan∠CAB= =2,
∴CF=2AE,OF=2OE.
又∵AE OE= ,CF OF=|k|,
∴k=±6.
∵点C在第二象限,
∴k=﹣6,
故选:B.
【分析】连接OC,过点A作AE⊥x轴于点E,过点C作CF⊥y轴于点F,通过角的计算找出∠AOE=∠COF,结合“∠AEO=90°,∠CFO=90°”可得出△AOE∽△COF,根据相似三角形的性质得出比例式,再由tan∠CAB=2,可得出CF OF的值,进而得到k的值.
8.【答案】10
【解析】【解答】解:坡度=1:2,即AB:BC=1:2,
且AC= =10 ,
解得:AB=10米,
故此时他与水平地面的距离为10米.
故答案为10.
【分析】如图,根据坡度为1:2,即可求得AB、BC的长度的比值,已知AC=10 米,利用勾股定理求出AB的值,即可得到答案.
9.【答案】或
【解析】【解答】解:分两种情况:
如图一,当是锐角三角形时,
在中,是边上的高,,,
,
,
,
在中,;
如图二,当是钝角三角形时,
在中,是边上的高,,,
,
,
,
在中,.
故答案为:或.
【分析】分类讨论:①当是锐角三角形时,②当是钝角三角形时,再分别画出图象并利用勾股定理求解即可。
10.【答案】解:过点B作BE⊥AC于点E,
在Rt△AEB中,AB=60m,sinA=,BE=ABsinA=60×=30,cosA=,
∴AE=60×=30m,
在Rt△CEB中,∠ACB=∠CBD﹣∠A=75°﹣30°=45°,
∴BE=CE=30m,
∴AC=AE+CE=(30+30)m,
在Rt△ADC中,sinA=,
则CD=(30+30)×=(15+15)m.
【解析】【分析】过点B作BE⊥AC于点E,在直角三角形AEB中,利用锐角三角函数定义求出AE的长,在直角三角形CEB中,利用锐角三角函数定义求出BE与CE的长,由AE+CE求出AC的长,即可求出CD的长.
11.【答案】(1)解:设反比例函数解析式为y= ,
将点A(2,4)代入,得:k=8,
∴反比例函数的解析式y=
(2)解:过点A作AE⊥x轴于点E,AE与BC交于点F,则CF=2,
∵cot∠ACB= = ,
∴AF=3,
∴EF=1,
∴点C的坐标为(0,1)
(3)解:当y=1时,由1= 可得x=8,
∴点B的坐标为(1,8),
∴BF=BC﹣CF=6,
∴AB= =3 ,
∴cos∠ABC= = =
【解析】【分析】(1)待定系数法求解可得;(2)作AE⊥x轴于点E,AE与BC交于点F,则CF=2,根据cot∠ACB= = 得AF=3,即可知EF,从而得出答案;(3)先求出点B的坐标.继而由勾股定理得出AB的长,最后由三角函数可得答案.
12.【答案】(1)解:设点M运动t秒(0≤t≤3),点M在AB上运动且MN⊥AB,如图,
∵△ABC为等边三角形,边长为6cm,
∴∠A=60°,∠AMN=90°,
∴,
由题意可知:BM=2tcm,AN=(6﹣t)cm,
∴AM=AB﹣BM=(6﹣t)cm,
∴,
解得:t=2,
∴点M运动的时间为2秒;
(2)解:∵△ABC是边长为4米的等边三角形,
∴AB=BC=AC=4,∠A=∠B=∠C=60°.
设笑笑出发x秒,一家人就得奖了,
则笑笑走了x米,笑笑的爸爸走了2x米,
∴CN=x米,BM=2x米,
∴AN=(4﹣x)米,AM=(4﹣2x)米,
∵四边形ANDM为平行四边形,
∴DN=AM=(4﹣2x)米,,
∴∠NDC=∠B=60°,∠DNC=∠A=60°,
∴∠DNC=∠C=∠NDC=60°,
∴△CDN是等边三角形,
∴DN=CD=CN=x米,
∴x=4﹣2x,
解得,
∴米.
即笑笑出发不到6秒,一家人就得奖了,那么妈妈所选的位置D距点C 米.
【解析】【分析】(1)设点M运动t秒,MN⊥AB,解直角三角形即可得到结论;
(2)设笑笑出发x秒,一家人就得奖了,则笑笑走了x米,笑笑的爸爸走了2x米,即CN=x,BM=2x,可求AN、AM,然后证明△CDN是等边三角形,可得:DN=CD=CN=x,列方程即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
28.2 解直角三角形及其应用一课一练
一、单选题
1.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值为( )
A. B. C. D.2
2.轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
A.25 B.25 C.50 D.25
3.如图,海中有一小岛,在点测得小岛在北偏东方向上,渔船从点出发由西向东航行到达点,在点测得小岛恰好在正北方向上,此时渔船与小岛的距离为.( )
A. B. C. D.
4.在Rt 中, ,若 ,则 的值为( )
A. B. C. D.
5.如图,修建抽水站时,沿着坡度为i=1: 的斜坡铺设水管.若测得水管A处铅垂高度为8 m,则所铺设水管AC的长度为( )
A.8m B.12m C.14m D.16m
6.如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF,tanα= ,则“人字梯”的顶端离地面的高度AD是( )
A.144cm B.180cm C.240cm D.360cm
7.如图,在反比例函数y= 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= 的图象上运动,若tan∠CAB=2,则k的值为( )
A.﹣3 B.﹣6 C.﹣9 D.﹣12
二、填空题
8.某人沿着坡度为 的坡面前进了 米,此时他与水平地面的垂直距离为 米.
9.在中,,是高,且,则 .
三、解答题
10.如图1是“东方之星”救援打捞现场图,小红据此构造出一个如图2所示的数学模型,已知:A、B、D三点在同一水平线上,CD⊥AD,∠A=30°,∠CBD=75°,AB=60m.
(1)求点B到AC的距离;
(2)求线段CD的长度.
四、综合题
11.已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且cot∠ACB=
求:
(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值.
五、实践探究题
12.如图
(1)问题提出
如图,△ABC为等边三角形,边长为6cm,动点M从点B出发,沿着三角形的三条边顺时针方向以2cm/s的速度运动,动点N从点C出发,沿着三角形的三条边逆时针方向以1cm/s的速度运动.动点M、N同时出发,当点M在AB上运动且MN⊥AB时,求点M运动的时间.
(2)问题解决
某小区有一个边长为4米的等边三角形花坛,六一将至,物业借助花坛△ABC举办了一个有奖活动,一家四口举着一根长绳在花坛三边任选位置站立(不能站在各边中点上),四人拉紧、拉直长绳后(长绳可有剩余)可得到一个四边形,如工作人员量得这个四边形是平行四边形,则可领取奖品一份.笑笑和爸爸、妈妈、奶奶一起参加活动,四人的方案是奶奶在A点站立不动,妈妈在△ABC边上某点D处站立不动,爸爸从点B出发,沿着花坛顺时针方向以2米/秒的速度走动(可看作花坛边上运动的点M),同时笑笑从点C出发,沿着花坛逆时针方向以1米/秒的速度走动(可看作花坛边上运动的点N).若笑笑出发不到6秒,一家人就得奖了,那么妈妈所选的位置D距点C多少米?
答案解析部分
1.【答案】C
【解析】【解答】如图,作CD⊥AB于点D,
则CD= ,BD= ,
故tan∠ABC= .
故答案为:C.
【分析】作CD⊥AB于点D,由网格图的特征用勾股定理可求出CD和BD的长,再由tan∠ABC=可求解。
2.【答案】D
【解析】【解答】解:根据题意,
∠1=∠2=30°,
∵∠ACD=60°,
∴∠ACB=30°+60°=90°,
∴∠CBA=75°﹣30°=45°,
△ABC为等腰直角三角形,
∵BC=50×0.5=25,
∴AC=BC=25(海里).
故答案为:D.
【分析】根据题意推出△ABC为等腰直角三角形,然后根据路程等于速度乘以时间算出BC的长,进而根据等腰三角形的性质得出AC的长。
3.【答案】D
【解析】【解答】解:如图,连接AC,
由题意得∠ACB=90°,∠ABC=60°,BC=10nmile,
∴AC=BC×tan∠ABC=10×tan60°=10×=10nmile.
故答案为:D.
【分析】连接AC根据∠ABC的正切函数可得AC=BC×tan∠ABC,从而代值计算可得答案.
4.【答案】A
【解析】【解答】解:∵∠C=90°,
∴AB==10,
∴cosA===.
故答案为:A.
【分析】根据勾股定理先求出AB长,然后根据余弦三角函数的定义计算即可.
5.【答案】D
【解析】【解答】解;∵该斜坡的坡度为i=1: ,
∴AB:BC=1: ,
∵AB=8m,
∴BC=8 m,
则AC= m.
故答案为:D.
【分析】利用解直角三角形的坡度问题进行求解即可。
6.【答案】B
【解析】【解答】解:如图:
根据题意可知:△AFO∽△ACD,OF= EF=30cm
∴ ,
∴
∴CD=72cm,
∵tanα=
∴
∴AD= =180cm.
故选:B.
【分析】根据题意可知:△AEO∽△ABD,从而可求得BD的长,然后根据锐角三角函数的定义可求得AD的长.
7.【答案】B
【解析】【解答】解:如图,连接OC,过点A作AE⊥y轴于点E,过点C作CF⊥y轴于点F,
∵由直线AB与反比例函数y= 的对称性可知A、B点关于O点对称,
∴AO=BO.
又∵AC=BC,
∴CO⊥AB.
∵∠AOE+∠AOF=90°,∠AOF+∠COF=90°,
∴∠AOE=∠COF,
又∵∠AEO=90°,∠CFO=90°,
∴△AOE∽△COF,
∴ = = ,
∵tan∠CAB= =2,
∴CF=2AE,OF=2OE.
又∵AE OE= ,CF OF=|k|,
∴k=±6.
∵点C在第二象限,
∴k=﹣6,
故选:B.
【分析】连接OC,过点A作AE⊥x轴于点E,过点C作CF⊥y轴于点F,通过角的计算找出∠AOE=∠COF,结合“∠AEO=90°,∠CFO=90°”可得出△AOE∽△COF,根据相似三角形的性质得出比例式,再由tan∠CAB=2,可得出CF OF的值,进而得到k的值.
8.【答案】10
【解析】【解答】解:坡度=1:2,即AB:BC=1:2,
且AC= =10 ,
解得:AB=10米,
故此时他与水平地面的距离为10米.
故答案为10.
【分析】如图,根据坡度为1:2,即可求得AB、BC的长度的比值,已知AC=10 米,利用勾股定理求出AB的值,即可得到答案.
9.【答案】或
【解析】【解答】解:分两种情况:
如图一,当是锐角三角形时,
在中,是边上的高,,,
,
,
,
在中,;
如图二,当是钝角三角形时,
在中,是边上的高,,,
,
,
,
在中,.
故答案为:或.
【分析】分类讨论:①当是锐角三角形时,②当是钝角三角形时,再分别画出图象并利用勾股定理求解即可。
10.【答案】解:过点B作BE⊥AC于点E,
在Rt△AEB中,AB=60m,sinA=,BE=ABsinA=60×=30,cosA=,
∴AE=60×=30m,
在Rt△CEB中,∠ACB=∠CBD﹣∠A=75°﹣30°=45°,
∴BE=CE=30m,
∴AC=AE+CE=(30+30)m,
在Rt△ADC中,sinA=,
则CD=(30+30)×=(15+15)m.
【解析】【分析】过点B作BE⊥AC于点E,在直角三角形AEB中,利用锐角三角函数定义求出AE的长,在直角三角形CEB中,利用锐角三角函数定义求出BE与CE的长,由AE+CE求出AC的长,即可求出CD的长.
11.【答案】(1)解:设反比例函数解析式为y= ,
将点A(2,4)代入,得:k=8,
∴反比例函数的解析式y=
(2)解:过点A作AE⊥x轴于点E,AE与BC交于点F,则CF=2,
∵cot∠ACB= = ,
∴AF=3,
∴EF=1,
∴点C的坐标为(0,1)
(3)解:当y=1时,由1= 可得x=8,
∴点B的坐标为(1,8),
∴BF=BC﹣CF=6,
∴AB= =3 ,
∴cos∠ABC= = =
【解析】【分析】(1)待定系数法求解可得;(2)作AE⊥x轴于点E,AE与BC交于点F,则CF=2,根据cot∠ACB= = 得AF=3,即可知EF,从而得出答案;(3)先求出点B的坐标.继而由勾股定理得出AB的长,最后由三角函数可得答案.
12.【答案】(1)解:设点M运动t秒(0≤t≤3),点M在AB上运动且MN⊥AB,如图,
∵△ABC为等边三角形,边长为6cm,
∴∠A=60°,∠AMN=90°,
∴,
由题意可知:BM=2tcm,AN=(6﹣t)cm,
∴AM=AB﹣BM=(6﹣t)cm,
∴,
解得:t=2,
∴点M运动的时间为2秒;
(2)解:∵△ABC是边长为4米的等边三角形,
∴AB=BC=AC=4,∠A=∠B=∠C=60°.
设笑笑出发x秒,一家人就得奖了,
则笑笑走了x米,笑笑的爸爸走了2x米,
∴CN=x米,BM=2x米,
∴AN=(4﹣x)米,AM=(4﹣2x)米,
∵四边形ANDM为平行四边形,
∴DN=AM=(4﹣2x)米,,
∴∠NDC=∠B=60°,∠DNC=∠A=60°,
∴∠DNC=∠C=∠NDC=60°,
∴△CDN是等边三角形,
∴DN=CD=CN=x米,
∴x=4﹣2x,
解得,
∴米.
即笑笑出发不到6秒,一家人就得奖了,那么妈妈所选的位置D距点C 米.
【解析】【分析】(1)设点M运动t秒,MN⊥AB,解直角三角形即可得到结论;
(2)设笑笑出发x秒,一家人就得奖了,则笑笑走了x米,笑笑的爸爸走了2x米,即CN=x,BM=2x,可求AN、AM,然后证明△CDN是等边三角形,可得:DN=CD=CN=x,列方程即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
