12.4 整式的除法(第2课时) 课件(共18张PPT)
文档属性
| 名称 | 12.4 整式的除法(第2课时) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 16:39:24 | ||
图片预览






文档简介
(共18张PPT)
12.4 整式的除法
第2课时 多项式除以单项式
数学(华东师大版)
八年级 上册
第12章 整式的乘除
学习目标
1.理解和掌握多项式除以单项式的运算法则;
2.会进行简单的多项式除以单项式的运算.
温故知新
计算下列各式,说说你是怎么想的?
(1)(am+bm)÷m;
(2)(a2+ab)÷a.
(1)(am+bm)÷m
(2)(a2+ab)÷a
=am÷m+bm÷m
=a+b
=a2÷a +ab÷a
=a+b
讲授新课
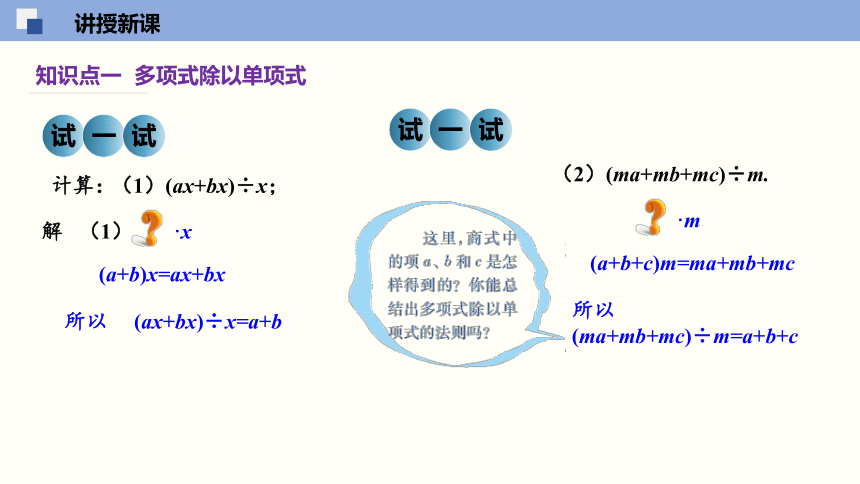
知识点一 多项式除以单项式
试
一
试
计算:
(1)(ax+bx)÷x;
解 (1)
·x
(a+b)x=ax+bx
所以 (ax+bx)÷x=a+b
试
一
试
(2)(ma+mb+mc)÷m.
·m
(a+b+c)m=ma+mb+mc
所以 (ma+mb+mc)÷m=a+b+c
讲授新课
知识要点
多项式除以单项式的法则
多项式除以单项式,先用这个多项式的 除以这个 ,再把所得的商 .
单项式
每一项
相加
关键:
应用法则是把多项式除以单项式转化为单项式除以单项式.
讲授新课
典例精析
例1
计算:
(1)(9x4-15x2+6x)÷3x
(2)(28a3b2c+a2b3-14a2b2)÷(-7a2b)
(1)(9x4-15x2+6x)÷3x
9x4
3x
=9x4÷3x
-15x2
-15x2÷3x
+6x
+6x÷3x
=(9÷3)x4-1-(15÷3)x2-1+(6÷3)x1-1
=3x3-5x+2
(2)(28a3b2c+a2b3-14a2b2)÷(-7a2b)
28a3b2c
-7a2b
=28a3b2c÷(-7a2b)
+a2b3
+a2b3÷(-7a2b)
-14a2b2
-14a2b2÷(-7a2b)
=-4a3-2b2-1c+( a2-2b3-1)-(-2a2-2b2-1)
=-4abc b2+2b
讲授新课
补充例题
计算:
(6xn+2+3xn+1-3xn-1)÷3xn-1
解:(6xn+2+3xn+1-3xn-1)÷3xn-1
=6xn+2÷3xn-1+3xn+1÷3xn-1-3xn-1÷3xn-1
=2xn+2-n+1+xn+1-n+1-1
=2x3+x2-1
思路归纳
如果除式中字母的指数是多项式,计算时要把它看作一个整体,且要添括号.
讲授新课
补充例题
化简:
[4(xy-1)2+(xy+2)(xy-2)]÷ xy
解:[4(xy-1)2+(xy+2)(xy-2)]÷ xy
=(4x2y2-8xy+4+x2y2-4)÷ xy
=(5x2y2-8xy)÷ xy
=20xy-32
思维点拨 进行整式的混合运算,应按照运算顺序进行化简.
当堂检测
1.计算(5m2+15m3n-20m4)÷(-5m2)的结果正确的是( )
A.4m2-3mn-1 B.1-3mn+4m2 C.-1-3m+4m2 D.4m2-3mn
【详解】解:(5m2+15m3n-20m4)÷(-5m2)
=4m2-3mn-1
故选:A.
当堂检测
2.长方形的面积为4a2-8ab+4a,若它的一边长为4a,则这个长方形的周长为( )
A.a-2b+1 B.10a-4b+2 C.5a-2b+1 D.8a-6b+2
【详解】解:∵长方形的面积为4a2-8ab+4a,若它的一边长为4a,
∴长方形的另一边的长为:(4a2-8ab+4a)÷4a=a-2b+1,
∴长方形的周长为:2×(4a+a-2b+1)=2×(5a-2b+1)=10a-4b+2,
故选:B.
当堂检测
3.计算(6ab-5a)÷a的结果是 .
【详解】解:∵(6ab-5a)÷a=6b-5,
故答案为:6b-5.
当堂检测
4.一个底面是正方形的长方体,高为3cm,底面正方形的边长为2cm,若它的高不变,底面正方形边长增加了acm,则它的体积增加了 cm3(用含a的代数式表示).
【详解】解:(a+2)2×3-22×3
=3(a2+4a+4)-12
=3a2+12a+12-12
=3a2+12a
∴它的体积增加了(3a2+12a)cm3.
故答案为:(3a2+12a).
当堂检测
5.先化简再求值:(a+b)(a-b)+(4ab3-8a2b2)÷4ab,其中a=2,b=-.
【详解】解:(a+b)(a-b)+(4ab3-8a2b2)÷4ab
=a2-b2+b2-2ab
=a2-2ab
当=2,b= 时,
原式=6.
当堂检测
6.某学校准备在一块长为(3a+2b)米,宽为(2a+b)米的长方形空地上修建一块长为(a+2b)米,宽为(3a-b)米的长方形草坪,四周铺设地砖(阴影部分),
(1)求铺设地砖的面积;(用含a,b的式子表示,结果化为最简)
(2)若a=3,b=4,铺设地砖的成本为50元/平方米,则完成铺设地砖需要多少元?
当堂检测
【详解】(1)解:∵长方形空地的长为(3a+2b)米,宽为(2a+b)米,
∴长方形空地的面积为(3a+2b)(2a+b)平方米,
∵长方形草坪的长为(a+2b)米,宽为(3a-b)米,
∴长方形草坪的面积为(a+2b)(3a-b)平方米,
∴铺设地砖的面积为:
(3a+2b)(2a+b)-(a+2b)(3a-b)=(3a2+2ab+4b2)m2,
答:铺设地砖的面积为(3a2+2ab+4b2)平方米;
当堂检测
(2)解:∵铺设地砖的面积为(3a2+2ab+4b2)平方米,
∴当a=3,b=4时,
原式=3×32+2×3×4+4×42=3×9+24+4×16=115,
∵铺设地砖的成本为50/元平方米,
∴115×50=5750(元).
答:完成铺设地砖需要5750元.
课堂小结
多项式除以单项式
运算法则
用这个多项式的每一项除以这个单项式,再把所得的商相加.
注意
1.计算时,多项式的各项要包括它们前面的符号,要注意符号的变化;
2.当被除式的项与除式的项相同时,商是1,不能把“1”漏掉.
谢 谢~
12.4 整式的除法
第2课时 多项式除以单项式
数学(华东师大版)
八年级 上册
第12章 整式的乘除
学习目标
1.理解和掌握多项式除以单项式的运算法则;
2.会进行简单的多项式除以单项式的运算.
温故知新
计算下列各式,说说你是怎么想的?
(1)(am+bm)÷m;
(2)(a2+ab)÷a.
(1)(am+bm)÷m
(2)(a2+ab)÷a
=am÷m+bm÷m
=a+b
=a2÷a +ab÷a
=a+b
讲授新课
知识点一 多项式除以单项式
试
一
试
计算:
(1)(ax+bx)÷x;
解 (1)
·x
(a+b)x=ax+bx
所以 (ax+bx)÷x=a+b
试
一
试
(2)(ma+mb+mc)÷m.
·m
(a+b+c)m=ma+mb+mc
所以 (ma+mb+mc)÷m=a+b+c
讲授新课
知识要点
多项式除以单项式的法则
多项式除以单项式,先用这个多项式的 除以这个 ,再把所得的商 .
单项式
每一项
相加
关键:
应用法则是把多项式除以单项式转化为单项式除以单项式.
讲授新课
典例精析
例1
计算:
(1)(9x4-15x2+6x)÷3x
(2)(28a3b2c+a2b3-14a2b2)÷(-7a2b)
(1)(9x4-15x2+6x)÷3x
9x4
3x
=9x4÷3x
-15x2
-15x2÷3x
+6x
+6x÷3x
=(9÷3)x4-1-(15÷3)x2-1+(6÷3)x1-1
=3x3-5x+2
(2)(28a3b2c+a2b3-14a2b2)÷(-7a2b)
28a3b2c
-7a2b
=28a3b2c÷(-7a2b)
+a2b3
+a2b3÷(-7a2b)
-14a2b2
-14a2b2÷(-7a2b)
=-4a3-2b2-1c+( a2-2b3-1)-(-2a2-2b2-1)
=-4abc b2+2b
讲授新课
补充例题
计算:
(6xn+2+3xn+1-3xn-1)÷3xn-1
解:(6xn+2+3xn+1-3xn-1)÷3xn-1
=6xn+2÷3xn-1+3xn+1÷3xn-1-3xn-1÷3xn-1
=2xn+2-n+1+xn+1-n+1-1
=2x3+x2-1
思路归纳
如果除式中字母的指数是多项式,计算时要把它看作一个整体,且要添括号.
讲授新课
补充例题
化简:
[4(xy-1)2+(xy+2)(xy-2)]÷ xy
解:[4(xy-1)2+(xy+2)(xy-2)]÷ xy
=(4x2y2-8xy+4+x2y2-4)÷ xy
=(5x2y2-8xy)÷ xy
=20xy-32
思维点拨 进行整式的混合运算,应按照运算顺序进行化简.
当堂检测
1.计算(5m2+15m3n-20m4)÷(-5m2)的结果正确的是( )
A.4m2-3mn-1 B.1-3mn+4m2 C.-1-3m+4m2 D.4m2-3mn
【详解】解:(5m2+15m3n-20m4)÷(-5m2)
=4m2-3mn-1
故选:A.
当堂检测
2.长方形的面积为4a2-8ab+4a,若它的一边长为4a,则这个长方形的周长为( )
A.a-2b+1 B.10a-4b+2 C.5a-2b+1 D.8a-6b+2
【详解】解:∵长方形的面积为4a2-8ab+4a,若它的一边长为4a,
∴长方形的另一边的长为:(4a2-8ab+4a)÷4a=a-2b+1,
∴长方形的周长为:2×(4a+a-2b+1)=2×(5a-2b+1)=10a-4b+2,
故选:B.
当堂检测
3.计算(6ab-5a)÷a的结果是 .
【详解】解:∵(6ab-5a)÷a=6b-5,
故答案为:6b-5.
当堂检测
4.一个底面是正方形的长方体,高为3cm,底面正方形的边长为2cm,若它的高不变,底面正方形边长增加了acm,则它的体积增加了 cm3(用含a的代数式表示).
【详解】解:(a+2)2×3-22×3
=3(a2+4a+4)-12
=3a2+12a+12-12
=3a2+12a
∴它的体积增加了(3a2+12a)cm3.
故答案为:(3a2+12a).
当堂检测
5.先化简再求值:(a+b)(a-b)+(4ab3-8a2b2)÷4ab,其中a=2,b=-.
【详解】解:(a+b)(a-b)+(4ab3-8a2b2)÷4ab
=a2-b2+b2-2ab
=a2-2ab
当=2,b= 时,
原式=6.
当堂检测
6.某学校准备在一块长为(3a+2b)米,宽为(2a+b)米的长方形空地上修建一块长为(a+2b)米,宽为(3a-b)米的长方形草坪,四周铺设地砖(阴影部分),
(1)求铺设地砖的面积;(用含a,b的式子表示,结果化为最简)
(2)若a=3,b=4,铺设地砖的成本为50元/平方米,则完成铺设地砖需要多少元?
当堂检测
【详解】(1)解:∵长方形空地的长为(3a+2b)米,宽为(2a+b)米,
∴长方形空地的面积为(3a+2b)(2a+b)平方米,
∵长方形草坪的长为(a+2b)米,宽为(3a-b)米,
∴长方形草坪的面积为(a+2b)(3a-b)平方米,
∴铺设地砖的面积为:
(3a+2b)(2a+b)-(a+2b)(3a-b)=(3a2+2ab+4b2)m2,
答:铺设地砖的面积为(3a2+2ab+4b2)平方米;
当堂检测
(2)解:∵铺设地砖的面积为(3a2+2ab+4b2)平方米,
∴当a=3,b=4时,
原式=3×32+2×3×4+4×42=3×9+24+4×16=115,
∵铺设地砖的成本为50/元平方米,
∴115×50=5750(元).
答:完成铺设地砖需要5750元.
课堂小结
多项式除以单项式
运算法则
用这个多项式的每一项除以这个单项式,再把所得的商相加.
注意
1.计算时,多项式的各项要包括它们前面的符号,要注意符号的变化;
2.当被除式的项与除式的项相同时,商是1,不能把“1”漏掉.
谢 谢~
