第五单元《简易方程》(单元复习课件)五年级数学上册 人教版(共22张PPT)
文档属性
| 名称 | 第五单元《简易方程》(单元复习课件)五年级数学上册 人教版(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 424.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-07 07:15:24 | ||
图片预览






文档简介
(共22张PPT)
第5单元
简易方程
人教版·五年级上册
单元知识体系梳理
1
重难点易错点剖析
2
变式巩固练习
3
综合拓展延伸
4
Text here
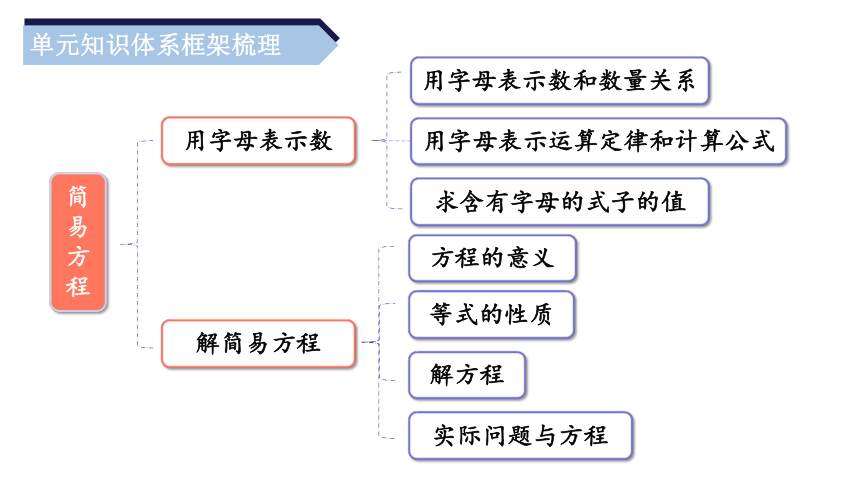
单元知识体系框架梳理
简易方程
解简易方程
用字母表示数和数量关系
用字母表示运算定律和计算公式
求含有字母的式子的值
用字母表示数
方程的意义
等式的性质
解方程
实际问题与方程
Text here
重难易错点剖析
Text here
重难易错点剖析
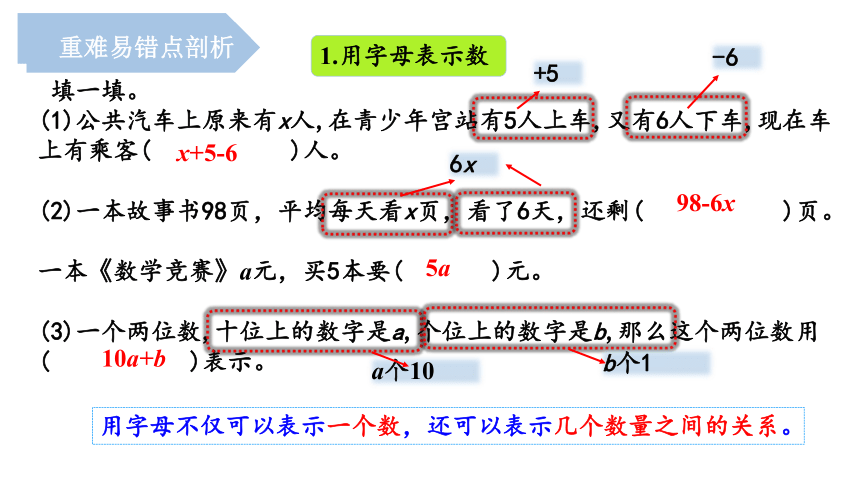
1.用字母表示数
填一填。
(1)公共汽车上原来有x人,在青少年宫站有5人上车,又有6人下车,现在车上有乘客( )人。
(2)一本故事书98页,平均每天看x页,看了6天,还剩( )页。
一本《数学竞赛》a元,买5本要( )元。
(3)一个两位数,十位上的数字是a,个位上的数字是b,那么这个两位数用( )表示。
x+5-6
98-6x
5a
10a+b
+5
-6
6x
a个10
b个1
用字母不仅可以表示一个数,还可以表示几个数量之间的关系。
Text here
重难易错点剖析
填一填,说一说。
(12.5+x)+8=12.5+( + )
4.5×a+6.5×a=a×( )
25-x-y=25 -( + )
s=v×( )
S平行四边形=a×( )
8
4.5+6.5
x
y
t
加法结合律
乘法分配律
x
连减的性质
速度、时间和路程的关系
h
平行四边形面积公式
2.用字母表示运算定律和计算公式
用字母可以表示我们学过的运算定律、运算性质、计算公式以及常用的数量关系。
Text here
重难易错点剖析
小华家12月底用电抄表读数是2231千瓦时,11月底用电抄表读数是m千瓦时。小华家12月份应缴电费a元,
(1)用含有字母的式子表示当地电费单价;
(2)当m=2130,a=56.56时,电费每千瓦时是多少元
(1) a÷(2231-m)
电费÷(12月底读数- 11月底读数) =单价
(2)当m=2130, a=56.56时,
a÷(2231-m)=56.56÷(2231-2130)=0.56(元/千瓦时)
把数值代入含有字母式子进行计算,结果注意不要忘了单位。
3.求含有字母式子的值
Text here
重难易错点剖析
省略乘号并化简下列各式。
2×x = t×47 = a×4 = x×y =
9×y+5×y = a+a+6 = 12×x-7×x = 2.5×c-c =
2x
47t
4a
xy
14y
2a+6
5x
1.5c
在用字母表示的式子里,乘号可以用“·”代替,或省略不写;利用乘法的分配律还可以对一些较复杂的式子进行化简。
4.含有字母式子的化简计算
Text here
重难易错点剖析
在方程后面画√。
6x+8 = 23 ( ) 8x-5 = 15×5 ( )
30a+5b ( ) 7x-8<36 ( )
10x = y ( ) (2.4+a)÷2.4 = 5 ( )
1÷8 = 0.125 ( ) 6x+8 = 9x-13 ( )
√
√
√
√
√
含有未知数的等式叫方程。判断一个式子是不是方程有两个条件:①是否等式;②是否含有未知数。二者缺一不可。
5.方程的意义
根据等式的性质填空。
(1)如果a=b(a、b均不为0),a+8=b+( );3a=b×( )
(2)如果3x = x+100,那么2x =( )
8
3
100
Text here
重难易错点剖析
等式的性质1 等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2 等式两边乘同一个数,或除以同一个不为0的数,左 右两边仍然相等。
6.等式的性质
x-3= 6
解: x-3+3= 6+3
x= 9
Text here
重难易错点剖析
7.方程的解法
解简单的方程,比如形如ax=b的方程 要灵活运用等式的性质1和性质2
x+35=91
解: x+35-35= 91-35
x= 56
用方程表示下面的数量关系,并求出方程的解。
(1)x加上35等于91。 (2)x的3倍等于57。
3x= 57
解: 3x÷3= 57÷3
x= 19
(3)x减3的差是6。 (4)x除以8等于1.3。
x÷8= 1.3
解: x÷8×8= 1.3×8
x= 10.4
Text here
重难易错点剖析
7.方程的解法
用方程表示下面的数量关系,并求出方程的解。
(1)70减去x的差是41.8。
(2)14除以x的商是3.5。
70-x=41.8
解: 70-x+x= 41.8+x
70= 41.8+x
41.8+x= 70
41.8+x-41.8= 70-41.8
x= 28.2
14÷x=3.5
解:14÷x×x=3.5×x
14=3.5x
3.5x=14
3.5x÷3.5=14÷3.5
x=4
解形如a-x=b的方程解:a-x+x=b+x b+x=a x=a-b
Text here
重难易错点剖析
7.方程的解法
解形如ax±b=c的方程,先把ax看作一个
整体,求出ax等于多少,再求x等于多少。
解方程。
8x-19=53 2x+0.8=12.7
解:8x-19+19=53+19
8x=72
8x÷8=72÷8
x=9
解:2x+0.8-0.8=12.7-0.8
2x=11.9
2x÷2=11.9÷2
x=5.95
Text here
重难易错点剖析
7.方程的解法
解方程:0.5(x+16)=30
方法一:0.5(x+16)=30
解:0.5x+8=30
0.5x+8-( )=30-( )
0.5x=22
0.5x÷( )=22 ÷( )
x=( )
方法二:0.5(x+16)=30
解: 0.5(x+16)÷0.5=30÷( )
x+16=60
x=( )
x+16-( )=60-( )
8
8
0.5
0.5
44
0.5
16
16
44
解形如a(x+b)=c(a≠0) 的方程时,可以把(x+b)看作一个整体,先求出这个整体是多少,再求出x的值;也可以运用乘法分配律将原方程展开,再求x的值。
Text here
重难易错点剖析
8.方程的应用
五(1)班女生折了 283颗幸运星,如果再折37颗,那么女生折的幸运星的总颗数就是男生的2倍。五(1)班男生折了多少颗幸运星?
解:设五(一)班男生折了x颗幸运星。
2x=283+37
2x=( )
x=( )
答:五(一)班男生折了( )颗幸运星。
320
160
160
找准题目中的等量关系是列方程解决问题的关键。
Text here
重难易错点剖析
8.方程的应用
雨燕是长距离飞行最快的鸟,每小时飞行的距离比信鸽每小时飞行距离的2倍还多22km,雨燕和信鸽每小时共飞行244km。雨燕和信鸽每小时各飞行多少千米?
解:设信鸽每小时飞行xkm。
2x+22+x=244
3x=( )
x=( )
雨燕每小时飞行:2×( )+22=( )(km)
222
74
答:雨燕每小时飞行( )km,信鸽每小时飞行( )km。
74
170
74
170
当两个量都是未知数,且存在倍数关系时,可先设1倍量为x,再把另一个量用含有x的式子表示出来,最后根据等量关系列出方程。
Text here
重难易错点剖析
8.方程的应用
列方程解决实际问题的步骤:
(1)找出未知数,用字母x表示;
(2)分析实际问题中的数量关系,找出等量关系,列方程;
(3)解方程并检验、作答。
一般情况下,列方程解决问题,都是求什么就设它为x。有时为解题方便,不直接设题目中所求的量为x,而是间接设另一个未知量为x,再根据等量关系列方程反而比较简洁。
Text here
深化练习
解方程。
6÷x=5
5x-3×4=43
解:6÷x×x=5×x
解:5x-12=43
5x=6
5x÷5=6÷5
x=1.2
5x-12+12=43+12
5x=55
5x÷5=55÷5
x=11
1.
Text here
深化练习
解方程。
1.
6(x+7.2)=58.2
8.7x-3.4x=5.406
解:6(x+7.2)÷6=58.2÷6
x+7.2=9.7
x+7.2-7.2=9.7-7.2
x=2.5
解:5.3x=5.406
5.3x÷5.3=5.406÷5.3
x=1.02
Text here
深化练习
2.
选一选:已知3x+7=25,则6x+1=( )。
3x+7=25
解:3x+7-7=25-7
3x÷3=18÷3
x=6
当x=6时,6x+1=37
B
A.22 B.37 C.30
解决问题的关键是先求出x的值,再把x的值代入到另一个式子中,求出另一个式子的值。
Text here
深化练习
3.
一个减法算式里的被减数、减数与差相加,得数是592。已知减数比差的3倍多4,减数是( )。
被减数+减数+差=( )
减数=差×3+( )
被减数=减数+差
592
4
解:设差为x。
4x+4+3x+4+x=592
8x+8=592
8x+8-8=592-8
8x÷8=584÷8
x=73
73×3+4=223
答:减数是223。
Text here
拓展练习
4.
李海和赵兰两人在周长为400m的环形跑道上同时从同一地点同向跑步。李海的速度是400米/分,赵兰的速度是320米/分,多少分钟后两人第一次相遇?相遇时赵兰跑了几圈?
解:设x分钟后两人第一次相遇。
400x-320x=400
( )x=400
x=( )
320×( )=( )(m)
( )÷400=( )(圈)
答:( )分钟后两人第一次相遇,相遇时赵兰跑了( )圈。
80
5
5
1600
1600
4
5
4
甲、乙两人在环形跑道上同时从同一地点同向跑步,属于追及问题。每追及一次,两人跑的路程差就是一个环形跑道的长度。
Text here
拓展练习
5.
学校食堂为同学们准备了相同数量的纯牛奶和酸奶。小明每次领取5瓶纯牛奶和3瓶酸奶分发给同学们,领取若干次后,纯牛奶没有了,酸奶还剩16瓶。学校食堂给同学们准备纯牛奶和酸奶各多少瓶?
解:设小明领了x次奶。
5x=3x+16
x=8
纯牛奶:5×8=40(瓶)
酸奶:3×8+16=40(瓶)。
答:学校食堂给同学们准备纯牛奶40瓶,酸奶40瓶。
第5单元
简易方程
人教版·五年级上册
单元知识体系梳理
1
重难点易错点剖析
2
变式巩固练习
3
综合拓展延伸
4
Text here
单元知识体系框架梳理
简易方程
解简易方程
用字母表示数和数量关系
用字母表示运算定律和计算公式
求含有字母的式子的值
用字母表示数
方程的意义
等式的性质
解方程
实际问题与方程
Text here
重难易错点剖析
Text here
重难易错点剖析
1.用字母表示数
填一填。
(1)公共汽车上原来有x人,在青少年宫站有5人上车,又有6人下车,现在车上有乘客( )人。
(2)一本故事书98页,平均每天看x页,看了6天,还剩( )页。
一本《数学竞赛》a元,买5本要( )元。
(3)一个两位数,十位上的数字是a,个位上的数字是b,那么这个两位数用( )表示。
x+5-6
98-6x
5a
10a+b
+5
-6
6x
a个10
b个1
用字母不仅可以表示一个数,还可以表示几个数量之间的关系。
Text here
重难易错点剖析
填一填,说一说。
(12.5+x)+8=12.5+( + )
4.5×a+6.5×a=a×( )
25-x-y=25 -( + )
s=v×( )
S平行四边形=a×( )
8
4.5+6.5
x
y
t
加法结合律
乘法分配律
x
连减的性质
速度、时间和路程的关系
h
平行四边形面积公式
2.用字母表示运算定律和计算公式
用字母可以表示我们学过的运算定律、运算性质、计算公式以及常用的数量关系。
Text here
重难易错点剖析
小华家12月底用电抄表读数是2231千瓦时,11月底用电抄表读数是m千瓦时。小华家12月份应缴电费a元,
(1)用含有字母的式子表示当地电费单价;
(2)当m=2130,a=56.56时,电费每千瓦时是多少元
(1) a÷(2231-m)
电费÷(12月底读数- 11月底读数) =单价
(2)当m=2130, a=56.56时,
a÷(2231-m)=56.56÷(2231-2130)=0.56(元/千瓦时)
把数值代入含有字母式子进行计算,结果注意不要忘了单位。
3.求含有字母式子的值
Text here
重难易错点剖析
省略乘号并化简下列各式。
2×x = t×47 = a×4 = x×y =
9×y+5×y = a+a+6 = 12×x-7×x = 2.5×c-c =
2x
47t
4a
xy
14y
2a+6
5x
1.5c
在用字母表示的式子里,乘号可以用“·”代替,或省略不写;利用乘法的分配律还可以对一些较复杂的式子进行化简。
4.含有字母式子的化简计算
Text here
重难易错点剖析
在方程后面画√。
6x+8 = 23 ( ) 8x-5 = 15×5 ( )
30a+5b ( ) 7x-8<36 ( )
10x = y ( ) (2.4+a)÷2.4 = 5 ( )
1÷8 = 0.125 ( ) 6x+8 = 9x-13 ( )
√
√
√
√
√
含有未知数的等式叫方程。判断一个式子是不是方程有两个条件:①是否等式;②是否含有未知数。二者缺一不可。
5.方程的意义
根据等式的性质填空。
(1)如果a=b(a、b均不为0),a+8=b+( );3a=b×( )
(2)如果3x = x+100,那么2x =( )
8
3
100
Text here
重难易错点剖析
等式的性质1 等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2 等式两边乘同一个数,或除以同一个不为0的数,左 右两边仍然相等。
6.等式的性质
x-3= 6
解: x-3+3= 6+3
x= 9
Text here
重难易错点剖析
7.方程的解法
解简单的方程,比如形如ax=b的方程 要灵活运用等式的性质1和性质2
x+35=91
解: x+35-35= 91-35
x= 56
用方程表示下面的数量关系,并求出方程的解。
(1)x加上35等于91。 (2)x的3倍等于57。
3x= 57
解: 3x÷3= 57÷3
x= 19
(3)x减3的差是6。 (4)x除以8等于1.3。
x÷8= 1.3
解: x÷8×8= 1.3×8
x= 10.4
Text here
重难易错点剖析
7.方程的解法
用方程表示下面的数量关系,并求出方程的解。
(1)70减去x的差是41.8。
(2)14除以x的商是3.5。
70-x=41.8
解: 70-x+x= 41.8+x
70= 41.8+x
41.8+x= 70
41.8+x-41.8= 70-41.8
x= 28.2
14÷x=3.5
解:14÷x×x=3.5×x
14=3.5x
3.5x=14
3.5x÷3.5=14÷3.5
x=4
解形如a-x=b的方程解:a-x+x=b+x b+x=a x=a-b
Text here
重难易错点剖析
7.方程的解法
解形如ax±b=c的方程,先把ax看作一个
整体,求出ax等于多少,再求x等于多少。
解方程。
8x-19=53 2x+0.8=12.7
解:8x-19+19=53+19
8x=72
8x÷8=72÷8
x=9
解:2x+0.8-0.8=12.7-0.8
2x=11.9
2x÷2=11.9÷2
x=5.95
Text here
重难易错点剖析
7.方程的解法
解方程:0.5(x+16)=30
方法一:0.5(x+16)=30
解:0.5x+8=30
0.5x+8-( )=30-( )
0.5x=22
0.5x÷( )=22 ÷( )
x=( )
方法二:0.5(x+16)=30
解: 0.5(x+16)÷0.5=30÷( )
x+16=60
x=( )
x+16-( )=60-( )
8
8
0.5
0.5
44
0.5
16
16
44
解形如a(x+b)=c(a≠0) 的方程时,可以把(x+b)看作一个整体,先求出这个整体是多少,再求出x的值;也可以运用乘法分配律将原方程展开,再求x的值。
Text here
重难易错点剖析
8.方程的应用
五(1)班女生折了 283颗幸运星,如果再折37颗,那么女生折的幸运星的总颗数就是男生的2倍。五(1)班男生折了多少颗幸运星?
解:设五(一)班男生折了x颗幸运星。
2x=283+37
2x=( )
x=( )
答:五(一)班男生折了( )颗幸运星。
320
160
160
找准题目中的等量关系是列方程解决问题的关键。
Text here
重难易错点剖析
8.方程的应用
雨燕是长距离飞行最快的鸟,每小时飞行的距离比信鸽每小时飞行距离的2倍还多22km,雨燕和信鸽每小时共飞行244km。雨燕和信鸽每小时各飞行多少千米?
解:设信鸽每小时飞行xkm。
2x+22+x=244
3x=( )
x=( )
雨燕每小时飞行:2×( )+22=( )(km)
222
74
答:雨燕每小时飞行( )km,信鸽每小时飞行( )km。
74
170
74
170
当两个量都是未知数,且存在倍数关系时,可先设1倍量为x,再把另一个量用含有x的式子表示出来,最后根据等量关系列出方程。
Text here
重难易错点剖析
8.方程的应用
列方程解决实际问题的步骤:
(1)找出未知数,用字母x表示;
(2)分析实际问题中的数量关系,找出等量关系,列方程;
(3)解方程并检验、作答。
一般情况下,列方程解决问题,都是求什么就设它为x。有时为解题方便,不直接设题目中所求的量为x,而是间接设另一个未知量为x,再根据等量关系列方程反而比较简洁。
Text here
深化练习
解方程。
6÷x=5
5x-3×4=43
解:6÷x×x=5×x
解:5x-12=43
5x=6
5x÷5=6÷5
x=1.2
5x-12+12=43+12
5x=55
5x÷5=55÷5
x=11
1.
Text here
深化练习
解方程。
1.
6(x+7.2)=58.2
8.7x-3.4x=5.406
解:6(x+7.2)÷6=58.2÷6
x+7.2=9.7
x+7.2-7.2=9.7-7.2
x=2.5
解:5.3x=5.406
5.3x÷5.3=5.406÷5.3
x=1.02
Text here
深化练习
2.
选一选:已知3x+7=25,则6x+1=( )。
3x+7=25
解:3x+7-7=25-7
3x÷3=18÷3
x=6
当x=6时,6x+1=37
B
A.22 B.37 C.30
解决问题的关键是先求出x的值,再把x的值代入到另一个式子中,求出另一个式子的值。
Text here
深化练习
3.
一个减法算式里的被减数、减数与差相加,得数是592。已知减数比差的3倍多4,减数是( )。
被减数+减数+差=( )
减数=差×3+( )
被减数=减数+差
592
4
解:设差为x。
4x+4+3x+4+x=592
8x+8=592
8x+8-8=592-8
8x÷8=584÷8
x=73
73×3+4=223
答:减数是223。
Text here
拓展练习
4.
李海和赵兰两人在周长为400m的环形跑道上同时从同一地点同向跑步。李海的速度是400米/分,赵兰的速度是320米/分,多少分钟后两人第一次相遇?相遇时赵兰跑了几圈?
解:设x分钟后两人第一次相遇。
400x-320x=400
( )x=400
x=( )
320×( )=( )(m)
( )÷400=( )(圈)
答:( )分钟后两人第一次相遇,相遇时赵兰跑了( )圈。
80
5
5
1600
1600
4
5
4
甲、乙两人在环形跑道上同时从同一地点同向跑步,属于追及问题。每追及一次,两人跑的路程差就是一个环形跑道的长度。
Text here
拓展练习
5.
学校食堂为同学们准备了相同数量的纯牛奶和酸奶。小明每次领取5瓶纯牛奶和3瓶酸奶分发给同学们,领取若干次后,纯牛奶没有了,酸奶还剩16瓶。学校食堂给同学们准备纯牛奶和酸奶各多少瓶?
解:设小明领了x次奶。
5x=3x+16
x=8
纯牛奶:5×8=40(瓶)
酸奶:3×8+16=40(瓶)。
答:学校食堂给同学们准备纯牛奶40瓶,酸奶40瓶。
