人教版数学八年级上册 14.2.2.1 完全平方公式 课件(共14张PPT)
文档属性
| 名称 | 人教版数学八年级上册 14.2.2.1 完全平方公式 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
14.2.2.1 完全平方公式
1.掌握完全平方公式的特征,能运用公式进行计算。
2.熟悉完全平方公式的常用变形,并且熟练应用变形解题。
学 习 目 标
多项式的乘法法则是什么?
用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
+
=
(a+b)
(p+q)
ap+aq
bp+bq
复 习 导 入
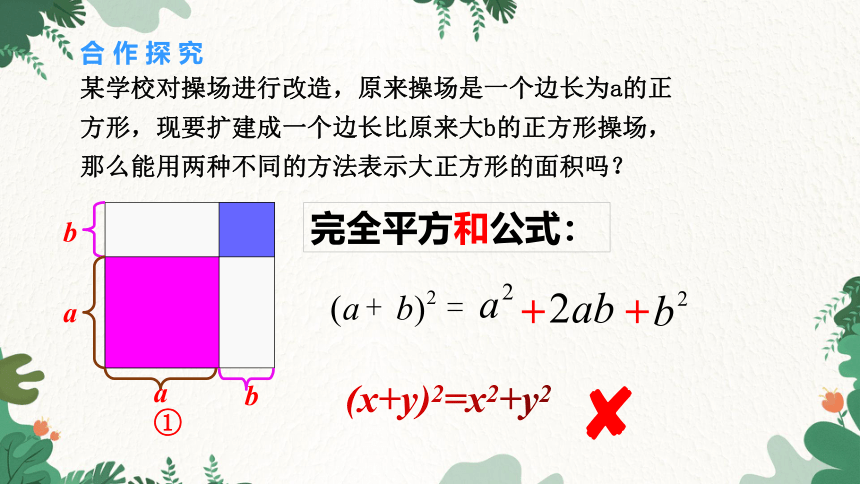
某学校对操场进行改造,原来操场是一个边长为a的正方形,现要扩建成一个边长比原来大b的正方形操场,那么能用两种不同的方法表示大正方形的面积吗?
b
a
b
a
①
+
+
完全平方和公式:
(x+y)2=x2+y2
合 作 探 究
某学校对操场进行改造,原来操场是一个边长为a的正方形,现要分割出一个边长比原来小b的正方形操场,那么能用两种不同的方法表示小正方形的面积吗?
b
a
b
a
②
完全平方差公式:
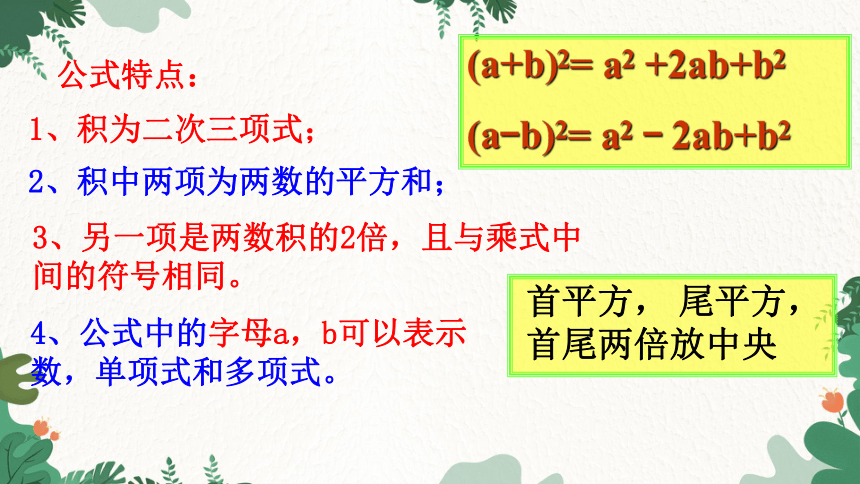
公式特点:
4、公式中的字母a,b可以表示
数,单项式和多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中
间的符号相同。
首平方, 尾平方,
首尾两倍放中央
解: (4m+n)2=
=16m2
(1)(4m+n)2
(a +b)2= a2 + 2 a b + b2
(4m)2
+2 (4m) n
+n2
+8mn
+n2
例1、运用完全平方公式计算:
典 例 精 析
解: (x-2y)2=
=x2
(2)(x-2y)2
(a - b)2= a2 - 2 ab + b2
x2
-2 x 2y
+(2y)2
-4xy
+4y2
(1) 1022
解: 1022
= (100+2)2
=10000+400+4
=10404
(2) 992
解: 992
= (100 –1)2
=10000 -200+1
=9801
例2、运用完全平方公式计算:
1.计算:(口答):
(1) (x+y)2
(2) (5a+b)2
(3) (3a-b)2
(4) (m-2n)2
=x2+2xy+y2
=25a2+10ab+b2
=9a2-6ab+b2
=m2-4mn+4n2
随 堂 练 习
2.若(y+a)2=y2-6y+b,则a,b的值分别为( )
A.a=3,b=9 B.a= -3,b= -9
C.a=3,b= -9 D,a= -3,b=9
3.下列运算中,错误的有( )
①(2x+y)2=4x2+y2; ②(a-3b)2=a2-9b2 ;
③(-x-y)2=x2-2xy+y2; ④(x- )2=x2-x+
A.1个 B.2个 C.3个 D.4个
D
C
运用完全平方公式计算:
(1) 1042
解: 1042
= (100+4)2
=10000+800+16
=10816
(2) 99.992
解: 99.992
= (100 –0.01)2
=10000 -2+0.0001
=9998.0001
拓 展 提 升
完全平方公式的数学表达式:
完全平方公式的文字叙述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
课 堂 总 结
谢谢大家!
14.2.2.1 完全平方公式
1.掌握完全平方公式的特征,能运用公式进行计算。
2.熟悉完全平方公式的常用变形,并且熟练应用变形解题。
学 习 目 标
多项式的乘法法则是什么?
用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
+
=
(a+b)
(p+q)
ap+aq
bp+bq
复 习 导 入
某学校对操场进行改造,原来操场是一个边长为a的正方形,现要扩建成一个边长比原来大b的正方形操场,那么能用两种不同的方法表示大正方形的面积吗?
b
a
b
a
①
+
+
完全平方和公式:
(x+y)2=x2+y2
合 作 探 究
某学校对操场进行改造,原来操场是一个边长为a的正方形,现要分割出一个边长比原来小b的正方形操场,那么能用两种不同的方法表示小正方形的面积吗?
b
a
b
a
②
完全平方差公式:
公式特点:
4、公式中的字母a,b可以表示
数,单项式和多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中
间的符号相同。
首平方, 尾平方,
首尾两倍放中央
解: (4m+n)2=
=16m2
(1)(4m+n)2
(a +b)2= a2 + 2 a b + b2
(4m)2
+2 (4m) n
+n2
+8mn
+n2
例1、运用完全平方公式计算:
典 例 精 析
解: (x-2y)2=
=x2
(2)(x-2y)2
(a - b)2= a2 - 2 ab + b2
x2
-2 x 2y
+(2y)2
-4xy
+4y2
(1) 1022
解: 1022
= (100+2)2
=10000+400+4
=10404
(2) 992
解: 992
= (100 –1)2
=10000 -200+1
=9801
例2、运用完全平方公式计算:
1.计算:(口答):
(1) (x+y)2
(2) (5a+b)2
(3) (3a-b)2
(4) (m-2n)2
=x2+2xy+y2
=25a2+10ab+b2
=9a2-6ab+b2
=m2-4mn+4n2
随 堂 练 习
2.若(y+a)2=y2-6y+b,则a,b的值分别为( )
A.a=3,b=9 B.a= -3,b= -9
C.a=3,b= -9 D,a= -3,b=9
3.下列运算中,错误的有( )
①(2x+y)2=4x2+y2; ②(a-3b)2=a2-9b2 ;
③(-x-y)2=x2-2xy+y2; ④(x- )2=x2-x+
A.1个 B.2个 C.3个 D.4个
D
C
运用完全平方公式计算:
(1) 1042
解: 1042
= (100+4)2
=10000+800+16
=10816
(2) 99.992
解: 99.992
= (100 –0.01)2
=10000 -2+0.0001
=9998.0001
拓 展 提 升
完全平方公式的数学表达式:
完全平方公式的文字叙述:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
课 堂 总 结
谢谢大家!
