13.2.2用坐标表示轴对称 课件(共28张PPT)人教版数学八年级上册
文档属性
| 名称 | 13.2.2用坐标表示轴对称 课件(共28张PPT)人教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 40.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 19:42:20 | ||
图片预览




文档简介
(共28张PPT)
第13章
轴对称
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
13.2.2
用坐标表示轴对称
情景引入
厦门大学校园衔山含湖、面朝大海,背靠万石植物园,一侧是南普陀寺,一侧是白城沙滩,与世界文化遗产鼓浪屿隔海相望。依海而建,依山傍水的地理环境让厦大素有“中国最美校园”的美誉。漫步厦大校园,各式各样中西结合的独特建筑或优雅或恢弘地矗立,让小明目不暇接、惊叹不已,小明在感受厦门大学独特魅力时,妈妈打来电话问小明的位置,聪明的小明想了想,就准确的告诉了妈妈,你能猜到小明是怎么做的吗?
新知探究
复习:
已知点A和直线l,画出点A关于直线l的对称点A′.
过点A作直线l的垂线,垂足为O,
在垂线上截取OA′=OA,
点A′就是点A关于直线l的对称点.
l
A
A′
┐
O
步骤一
步骤二
步骤三
新知探究
思考:
x
y
O
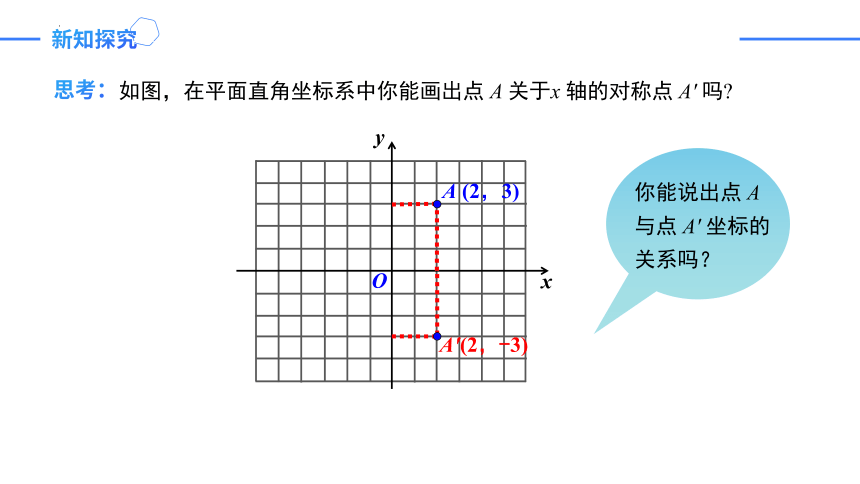
如图,在平面直角坐标系中你能画出点 A 关于x 轴的对称点 A′ 吗
A (2,3)
A′(2,-3)
你能说出点 A 与点 A' 坐标的关系吗?
新知探究
思考:
x
y
O
A(2,3)
A’
B
C
D
E
A
B’
C’
D’
E’
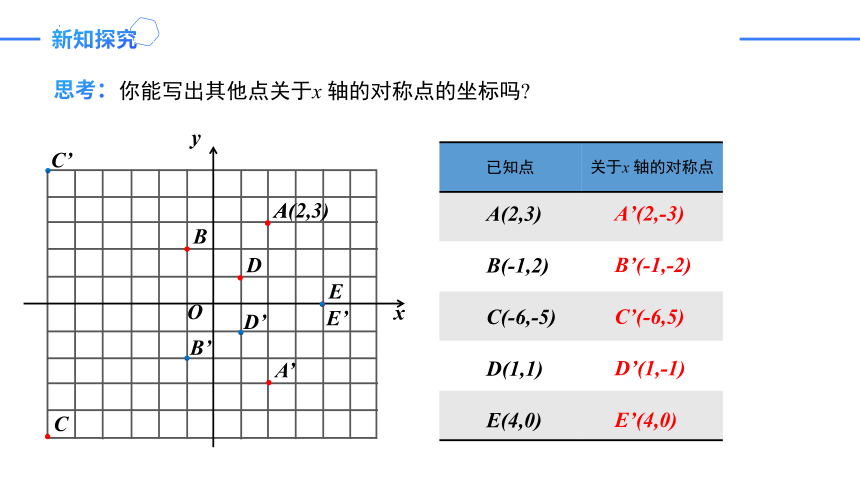
你能写出其他点关于x 轴的对称点的坐标吗
已知点 关于x 轴的对称点
A(2,3)
B(-1,2)
C(-6,-5)
D(1,1)
E(4,0)
A’(2,-3)
B’(-1,-2)
C’(-6,5)
D’(1,-1)
E’(4,0)
新知探究
思考:
x
y
O
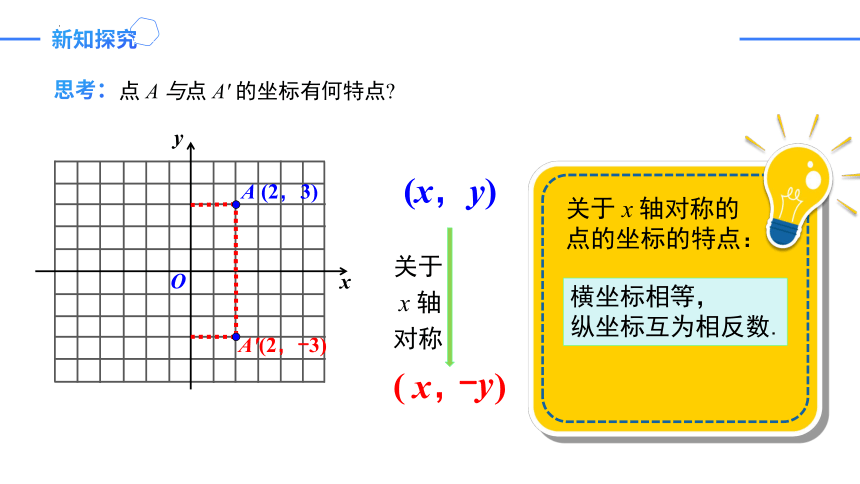
点 A 与点 A′ 的坐标有何特点
A (2,3)
A′(2,-3)
(x,y)
关于
x 轴
对称
( , )
x
-y
关于 x 轴对称的点的坐标的特点:
横坐标相等,
纵坐标互为相反数.
新知探究
思考:
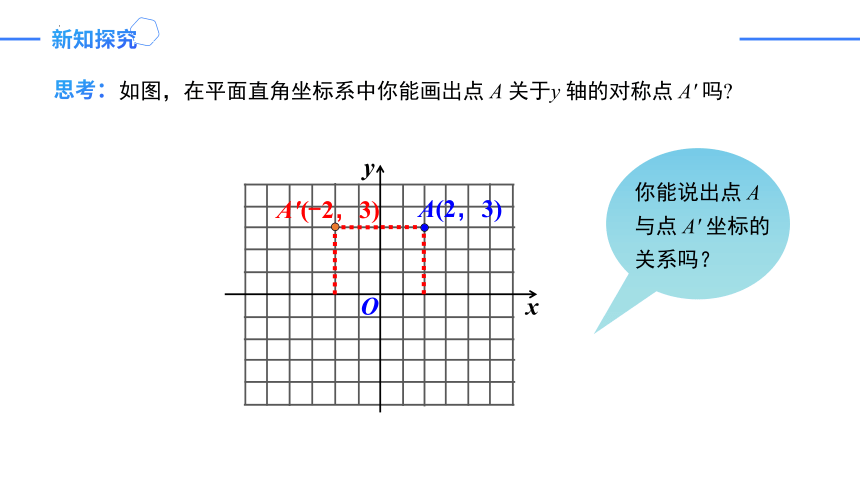
如图,在平面直角坐标系中你能画出点 A 关于y 轴的对称点 A′ 吗
你能说出点 A 与点 A' 坐标的关系吗?
x
y
O
A(2,3)
A′(-2,3)
新知探究
思考:
x
y
O
A(2,3)
A’
B
C
D
E
A
B’
C’
D’
E’
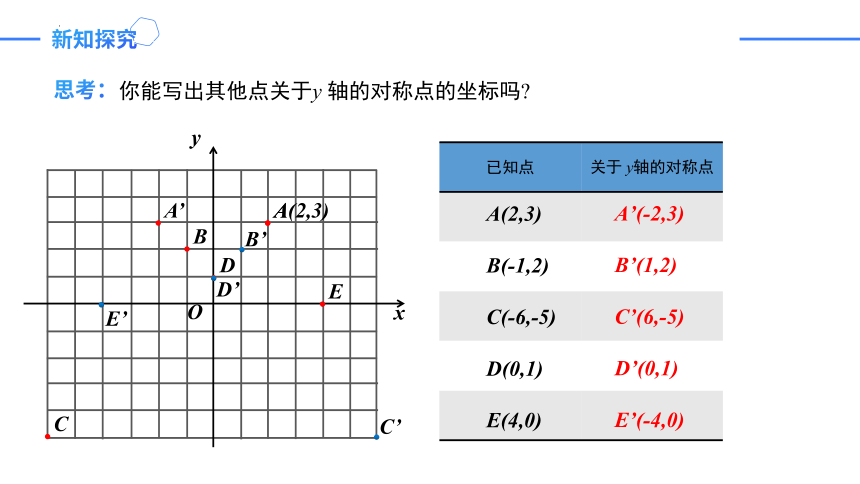
你能写出其他点关于y 轴的对称点的坐标吗
已知点 关于 y轴的对称点
A(2,3)
B(-1,2)
C(-6,-5)
D(0,1)
E(4,0)
A’(-2,3)
B’(1,2)
C’(6,-5)
D’(0,1)
E’(-4,0)
新知探究
思考:
x
y
O
点 A 与点 A′ 的坐标有何特点
A (2,3)
A′(2,-3)
关于 y轴对称的点的坐标的特点:
纵坐标相等,
横坐标互为相反数.
(x,y)
关于 y 轴
对称
( , )
-x
y
新知探究
思考:
x
y
O
如图,在平面直角坐标系中你能画出点 A 关于原点的对称点 A′ 吗
A (2,3)
A′(-2,-3)
你能说出点 A 与点 A' 坐标的关系吗?
新知探究
思考:
x
y
O
A(2,3)
A’
B
C
D
E
A
B’
C’
D’
E’
你能写出其他点关于原点的对称点的坐标吗
已知点 关于原点的对称点
A(2,3)
B(-1,2)
C(-6,-5)
D(1,1)
E(4,0)
A’(-2,-3)
B’(1,-2)
C’(6,5)
D’(-1,-1)
E’(-4,0)
新知探究
思考:
点 A 与点 A′ 的坐标有何特点
(x,y)
关于
原点
对称
( , )
-x
-y
关于原点对称的点的坐标的特点:
横坐标互为相反数,
纵坐标互为相反数.
x
y
O
A (2,3)
A′(-2,-3)
新知探究
●
A(3,2)
●
A′(3,-2)
●
A′′(-3,2)
横坐标不变,纵
坐标互为相反数
纵坐标不变,横
坐标互为相反数
o
x
y
●
A′′′ (-3,-2)
横坐标,纵坐标均互为相反数
关于x轴对称
关于y轴对称
关于原点对称
典例精析
例1
1. 点 P (-5,6) 与点 Q 关于 x 轴对称,则点 Q 的坐标为__________.
2. 点 M (a,-5) 与点 N (-2,b) 关于 x 轴对称,则 a =_____,b =_____.
(-5,-6)
-2
5
3. 点 P (-5,6) 与点 Q 关于 y 轴对称,则点 Q 的坐标为________.
4. 点 M (a,-5) 与点 N (-2,b) 关于 y 轴对称,则 a =
____, b =_____.
5. 点 M (a,-5) 与点 N (-2,b) 关于原点对称,则 a =
____, b =_____.
(5,6)
2
-5
-2
5
新知探究
思考:
如图,已知网格中每个小正方形的边长均为1.
(1)作出△ABC关于y轴的对称图形△A′B′C′,并分别写出A′,B′,C′三点的坐标;
(2)求△ABC的面积.
(2)S△ABC=
解:(1)如右图所示;
A′(3,3),B′(5,1),C′(1,0);
A’
B’
C’
归纳总结
新知探究
在直角坐标系中画与已知图形关于某直线成轴对称的图形的方法:
计算:计算出已知图形中的一些特殊点的对称点的坐标;
描点:根据对称点的坐标描点;
连接:按原图对应点连接所描各点得到对称图形.
所找的特殊点一定要能确定原图形, 否则画出的图形与原图形不一定成轴对称.
典例精析
例2
A’(-4,-1)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
C(-3,2)
B(-1,-1)
A(-4,1)
·
·
·
如图,利用关于坐标轴对称的点的坐标的特点,分别作出△ABC关于X轴和y 轴对称的图形.
B’’(1,-1)
C’’(3,2)
A’’(4,1)
·
·
·
·
·
·
C’(-3,-2)
B’(-1,1)
典例精析
例3
已知点 A (2a-b,5+a),B (2b-1,-a+b).
(1) 若点 A、B 关于 x 轴对称,求 a、b 的值;
(2) 若 A、B 关于 y 轴对称,求 (4a+b)2023的值.
解:(1) ∵ 点 A、B 关于 x 轴对称,
∴ 2a-b=2b-1,5+a-a+b=0.
解得 a=-8,b=-5.
(2) ∵ A、B 关于 y 轴对称,
∴ 2a-b+2b-1=0,5+a=-a+b.
解得 a=-1,b=3.
∴ (4a+b)2023 =-1.
典例精析
例4
已知点 P (a+1,2a-1)关于 x 轴的对称点在第一象限,求 a 的取值范围.
解:依题意得 P 点在第四象限,
解得
即 a 的取值范围是
归纳总结
在坐标系中作已知
图形的对称图形
关键要明确点关于 x 轴、y 轴
对称的点的坐标变化规律,
然后正确描出对称点的位置
关于 x 轴对称,横同纵反;
关于 y 轴对称,横反纵同;
关于原点对称,横纵都反.
轴对称的坐标表示
关于坐标轴对称的点
的坐标特征
当堂检测
1.已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
2
4
6
-20
2.在平面直角坐标系中,点(x,y)关于直线x=1对称点的 坐标是_____________.
在平面直角坐标系中,点(x,y)关于直线y=-1对称点的坐标是_____________.
(-x+2,y)
(x,-y-2)
3.(1)若mn=0,则点P(m,n)必定在__________上;
(2)已知点P(a,b),Q(2,4),且PQ∥x轴,则b的值为____.
坐标轴
4
当堂检测
5.已知矩形ABCD的顶点坐标分别为A(-7,-2),B(-7,-5), C(-3,-5),D(-3,-2),以y 轴为对称轴作轴对称,求矩形A’B’C’D’的坐标。
解:矩形A’B’C’D’的顶点坐标分别为:
A’(7,-2),B’(7,-5),C’(3,-5),D’(3,-2).
4. 已知点 A (2a + b,-4),B (3,a - 2b) 关于 x 轴对称,问点 C (a,b) 在第几象限?
解:∵ 点 A (2a + b,-4),B (3,a - 2b) 关于 x 轴对称,
∴ 2a + b = 3,-4 + a - 2b = 0,
解得 a = 2,b = -1.
∴ 点 C (2,-1) 在第四象限.
当堂检测
6.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,2),C(5,2).
(1)作出△ABC关于y轴的轴对称图形,并写出其顶点坐标.
(2)作出△ABC关于x轴的轴对称图形,并写出其顶点坐标.
B
●
●
●
C
A
●
A1(-2,4)
●
C1(-5,2)
●
B1(-1,2)
●
B2(1,-2)
●
C2(5,-2)
●
A2(-2,4)
o
x
y
(2,4)
(1,2)
(5,2)
当堂检测
7.在平面直角坐标系中,O为坐标原点,点A的坐标为(2x-3,x-2y),它关于x轴的对称点A1的坐标为(x+3,y-4),关于y轴的对称点为A2.
(1)求A1,A2的坐标;
(2)求证:O为线段A1A2的中点.
解:(1)由题意,得
解得
∴A1(9,-2),A2(-9,2);
当堂检测
8.在平面直角坐标系中, △ABC的顶点坐标分别为A(-4,1), B(-2,1),
C(-2,3).
(1)作△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向下平移4个单位长度;
做出平移后的△A2B2C2;
(3)求四边形AA2B2C的面积.
当堂检测
(1)△ABC的顶点坐标分别为A(-4,1), B(-2,1), C(-2,3), 关于y轴对称的点分别为A1(4,1), B1(2,1), C1(2,3).
(2)△ABC的顶点坐标分别为A(-4,1), B(-2,1), C(-2,3), 向下平移4个单位长度的点分别为A2(-4,-3), B2(-2,-3), C2(-2,-1).
当堂检测
(3)四边形AA2B2C为梯形, 其中上底AA2=4, 下底B2C=6, 高A2B2=2, 所以四边形AA2B2C的面积为10.
第13章
轴对称
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
13.2.2
用坐标表示轴对称
情景引入
厦门大学校园衔山含湖、面朝大海,背靠万石植物园,一侧是南普陀寺,一侧是白城沙滩,与世界文化遗产鼓浪屿隔海相望。依海而建,依山傍水的地理环境让厦大素有“中国最美校园”的美誉。漫步厦大校园,各式各样中西结合的独特建筑或优雅或恢弘地矗立,让小明目不暇接、惊叹不已,小明在感受厦门大学独特魅力时,妈妈打来电话问小明的位置,聪明的小明想了想,就准确的告诉了妈妈,你能猜到小明是怎么做的吗?
新知探究
复习:
已知点A和直线l,画出点A关于直线l的对称点A′.
过点A作直线l的垂线,垂足为O,
在垂线上截取OA′=OA,
点A′就是点A关于直线l的对称点.
l
A
A′
┐
O
步骤一
步骤二
步骤三
新知探究
思考:
x
y
O
如图,在平面直角坐标系中你能画出点 A 关于x 轴的对称点 A′ 吗
A (2,3)
A′(2,-3)
你能说出点 A 与点 A' 坐标的关系吗?
新知探究
思考:
x
y
O
A(2,3)
A’
B
C
D
E
A
B’
C’
D’
E’
你能写出其他点关于x 轴的对称点的坐标吗
已知点 关于x 轴的对称点
A(2,3)
B(-1,2)
C(-6,-5)
D(1,1)
E(4,0)
A’(2,-3)
B’(-1,-2)
C’(-6,5)
D’(1,-1)
E’(4,0)
新知探究
思考:
x
y
O
点 A 与点 A′ 的坐标有何特点
A (2,3)
A′(2,-3)
(x,y)
关于
x 轴
对称
( , )
x
-y
关于 x 轴对称的点的坐标的特点:
横坐标相等,
纵坐标互为相反数.
新知探究
思考:
如图,在平面直角坐标系中你能画出点 A 关于y 轴的对称点 A′ 吗
你能说出点 A 与点 A' 坐标的关系吗?
x
y
O
A(2,3)
A′(-2,3)
新知探究
思考:
x
y
O
A(2,3)
A’
B
C
D
E
A
B’
C’
D’
E’
你能写出其他点关于y 轴的对称点的坐标吗
已知点 关于 y轴的对称点
A(2,3)
B(-1,2)
C(-6,-5)
D(0,1)
E(4,0)
A’(-2,3)
B’(1,2)
C’(6,-5)
D’(0,1)
E’(-4,0)
新知探究
思考:
x
y
O
点 A 与点 A′ 的坐标有何特点
A (2,3)
A′(2,-3)
关于 y轴对称的点的坐标的特点:
纵坐标相等,
横坐标互为相反数.
(x,y)
关于 y 轴
对称
( , )
-x
y
新知探究
思考:
x
y
O
如图,在平面直角坐标系中你能画出点 A 关于原点的对称点 A′ 吗
A (2,3)
A′(-2,-3)
你能说出点 A 与点 A' 坐标的关系吗?
新知探究
思考:
x
y
O
A(2,3)
A’
B
C
D
E
A
B’
C’
D’
E’
你能写出其他点关于原点的对称点的坐标吗
已知点 关于原点的对称点
A(2,3)
B(-1,2)
C(-6,-5)
D(1,1)
E(4,0)
A’(-2,-3)
B’(1,-2)
C’(6,5)
D’(-1,-1)
E’(-4,0)
新知探究
思考:
点 A 与点 A′ 的坐标有何特点
(x,y)
关于
原点
对称
( , )
-x
-y
关于原点对称的点的坐标的特点:
横坐标互为相反数,
纵坐标互为相反数.
x
y
O
A (2,3)
A′(-2,-3)
新知探究
●
A(3,2)
●
A′(3,-2)
●
A′′(-3,2)
横坐标不变,纵
坐标互为相反数
纵坐标不变,横
坐标互为相反数
o
x
y
●
A′′′ (-3,-2)
横坐标,纵坐标均互为相反数
关于x轴对称
关于y轴对称
关于原点对称
典例精析
例1
1. 点 P (-5,6) 与点 Q 关于 x 轴对称,则点 Q 的坐标为__________.
2. 点 M (a,-5) 与点 N (-2,b) 关于 x 轴对称,则 a =_____,b =_____.
(-5,-6)
-2
5
3. 点 P (-5,6) 与点 Q 关于 y 轴对称,则点 Q 的坐标为________.
4. 点 M (a,-5) 与点 N (-2,b) 关于 y 轴对称,则 a =
____, b =_____.
5. 点 M (a,-5) 与点 N (-2,b) 关于原点对称,则 a =
____, b =_____.
(5,6)
2
-5
-2
5
新知探究
思考:
如图,已知网格中每个小正方形的边长均为1.
(1)作出△ABC关于y轴的对称图形△A′B′C′,并分别写出A′,B′,C′三点的坐标;
(2)求△ABC的面积.
(2)S△ABC=
解:(1)如右图所示;
A′(3,3),B′(5,1),C′(1,0);
A’
B’
C’
归纳总结
新知探究
在直角坐标系中画与已知图形关于某直线成轴对称的图形的方法:
计算:计算出已知图形中的一些特殊点的对称点的坐标;
描点:根据对称点的坐标描点;
连接:按原图对应点连接所描各点得到对称图形.
所找的特殊点一定要能确定原图形, 否则画出的图形与原图形不一定成轴对称.
典例精析
例2
A’(-4,-1)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
C(-3,2)
B(-1,-1)
A(-4,1)
·
·
·
如图,利用关于坐标轴对称的点的坐标的特点,分别作出△ABC关于X轴和y 轴对称的图形.
B’’(1,-1)
C’’(3,2)
A’’(4,1)
·
·
·
·
·
·
C’(-3,-2)
B’(-1,1)
典例精析
例3
已知点 A (2a-b,5+a),B (2b-1,-a+b).
(1) 若点 A、B 关于 x 轴对称,求 a、b 的值;
(2) 若 A、B 关于 y 轴对称,求 (4a+b)2023的值.
解:(1) ∵ 点 A、B 关于 x 轴对称,
∴ 2a-b=2b-1,5+a-a+b=0.
解得 a=-8,b=-5.
(2) ∵ A、B 关于 y 轴对称,
∴ 2a-b+2b-1=0,5+a=-a+b.
解得 a=-1,b=3.
∴ (4a+b)2023 =-1.
典例精析
例4
已知点 P (a+1,2a-1)关于 x 轴的对称点在第一象限,求 a 的取值范围.
解:依题意得 P 点在第四象限,
解得
即 a 的取值范围是
归纳总结
在坐标系中作已知
图形的对称图形
关键要明确点关于 x 轴、y 轴
对称的点的坐标变化规律,
然后正确描出对称点的位置
关于 x 轴对称,横同纵反;
关于 y 轴对称,横反纵同;
关于原点对称,横纵都反.
轴对称的坐标表示
关于坐标轴对称的点
的坐标特征
当堂检测
1.已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
2
4
6
-20
2.在平面直角坐标系中,点(x,y)关于直线x=1对称点的 坐标是_____________.
在平面直角坐标系中,点(x,y)关于直线y=-1对称点的坐标是_____________.
(-x+2,y)
(x,-y-2)
3.(1)若mn=0,则点P(m,n)必定在__________上;
(2)已知点P(a,b),Q(2,4),且PQ∥x轴,则b的值为____.
坐标轴
4
当堂检测
5.已知矩形ABCD的顶点坐标分别为A(-7,-2),B(-7,-5), C(-3,-5),D(-3,-2),以y 轴为对称轴作轴对称,求矩形A’B’C’D’的坐标。
解:矩形A’B’C’D’的顶点坐标分别为:
A’(7,-2),B’(7,-5),C’(3,-5),D’(3,-2).
4. 已知点 A (2a + b,-4),B (3,a - 2b) 关于 x 轴对称,问点 C (a,b) 在第几象限?
解:∵ 点 A (2a + b,-4),B (3,a - 2b) 关于 x 轴对称,
∴ 2a + b = 3,-4 + a - 2b = 0,
解得 a = 2,b = -1.
∴ 点 C (2,-1) 在第四象限.
当堂检测
6.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,2),C(5,2).
(1)作出△ABC关于y轴的轴对称图形,并写出其顶点坐标.
(2)作出△ABC关于x轴的轴对称图形,并写出其顶点坐标.
B
●
●
●
C
A
●
A1(-2,4)
●
C1(-5,2)
●
B1(-1,2)
●
B2(1,-2)
●
C2(5,-2)
●
A2(-2,4)
o
x
y
(2,4)
(1,2)
(5,2)
当堂检测
7.在平面直角坐标系中,O为坐标原点,点A的坐标为(2x-3,x-2y),它关于x轴的对称点A1的坐标为(x+3,y-4),关于y轴的对称点为A2.
(1)求A1,A2的坐标;
(2)求证:O为线段A1A2的中点.
解:(1)由题意,得
解得
∴A1(9,-2),A2(-9,2);
当堂检测
8.在平面直角坐标系中, △ABC的顶点坐标分别为A(-4,1), B(-2,1),
C(-2,3).
(1)作△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向下平移4个单位长度;
做出平移后的△A2B2C2;
(3)求四边形AA2B2C的面积.
当堂检测
(1)△ABC的顶点坐标分别为A(-4,1), B(-2,1), C(-2,3), 关于y轴对称的点分别为A1(4,1), B1(2,1), C1(2,3).
(2)△ABC的顶点坐标分别为A(-4,1), B(-2,1), C(-2,3), 向下平移4个单位长度的点分别为A2(-4,-3), B2(-2,-3), C2(-2,-1).
当堂检测
(3)四边形AA2B2C为梯形, 其中上底AA2=4, 下底B2C=6, 高A2B2=2, 所以四边形AA2B2C的面积为10.
