3.1 字母表示数 课件(共25张PPT) 七年级数学上册(北师大版)
文档属性
| 名称 | 3.1 字母表示数 课件(共25张PPT) 七年级数学上册(北师大版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 508.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-08 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
第三章 整式及其加减
第1节 字母表示数
导入新课
讲授新课
课堂小结
随堂训练
学习目标
1.理解用字母表示数的意义.(重点)
2.能用字母表示以前学过的运算律和计算公式.
3.能用字母表示一些简单问题中的数量关系和变化规律.(难点)
新课引入
长方形的周长和面积:
正方形的周长和面积:
平行四边形的面积:
梯形的面积:
圆的周长和面积:
长方体的体积:
正方体的体积:
球的表面积和体积:
圆柱的体积:
圆锥的体积:
路程、速度、时间的关系:
新课引入
1只青蛙1张嘴,2只眼睛4条腿,扑通1声跳下水;
2只青蛙2张嘴,4只眼睛8条腿,扑通2声跳下水;
3只青蛙3张嘴, 6只眼睛12条腿,扑通3声跳下水;
………….
你觉得这首歌唱得完吗?
你能用数学知识,一句话把这首儿歌唱完吗?
接下来怎么唱?
合作探究
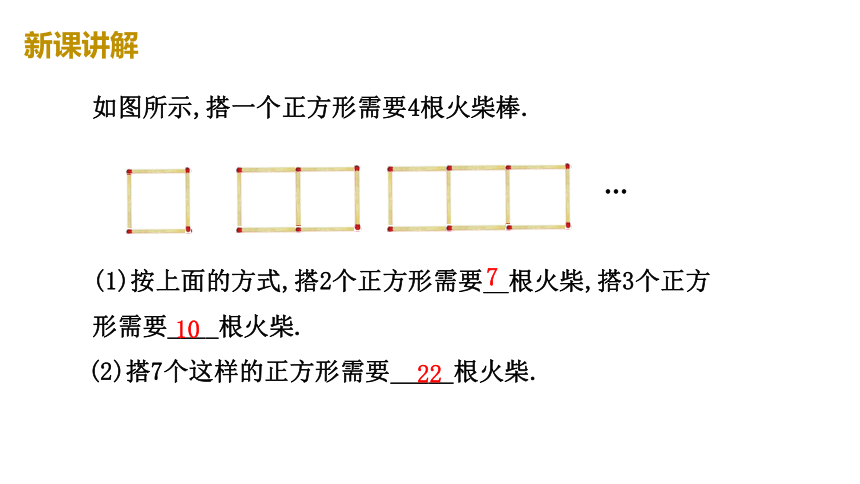
知识点1 用字母表示规律
新课讲解
十只青蛙____张嘴,____只眼睛____条腿,____声扑通跳下水;
一百只青蛙____张嘴,____只眼睛____条腿,____声扑通跳下水;
……
a只青蛙_____张嘴,_______只眼睛_______条腿,_______声扑通跳下水;
a
a
10
20
40
10
100
200
400
100
字母a表示什么?
字母可以表示数
新课讲解
用字母表示数的书写规则
① 数与字母、字母与字母相乘时省略乘号,数与字母相乘时数字在前;
② 出现多个字母时,字母按照26个字母顺序排列;
③ 相同字母相乘时应写成幂的形式;
④ 1或-1与字母相乘时,1通常省略不写;
⑤ 式子中出现除法运算时,一般按分数形式来写,带分数与字母相乘时,把带分数化成假分数.
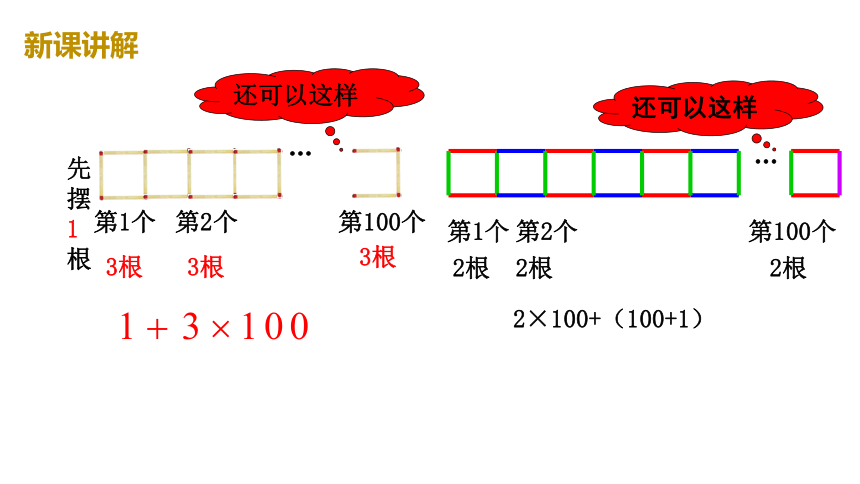
如图所示,搭一个正方形需要4根火柴棒.
…
(1)按上面的方式,搭2个正方形需要__根火柴,搭3个正方形需要____根火柴.
(2)搭7个这样的正方形需要_____根火柴.
7
10
22
新课讲解
(3)搭100个这样的正方形需要多少根火柴
第1个
4根
第2个
第100个
3根
3根
…
有没有其他计算方法?
新课讲解
先摆 1根
第1个
3根
第100个
…
第2个
3根
3根
还可以这样
…
第1个
2根
第2个
2根
第100个
2根
2×100+(100+1)
还可以这样
新课讲解
…
第1个
4根
第100个
4根
…
还可以这样
新课讲解
(4)如果用x表示所搭正方形的个数, 那么搭x个这样的正方形需要多少根火柴
第1个
4根
第2个
第100个
3根
3根
…
新课讲解
先摆 1根
第1个
3根
第100个
…
第2个
3根
3根
或者这样
新课讲解
水平方向
2+2
3+3
4+4
第1个
第2个
第3个
第4个
…
第x个
x+x
1+1
竖直方向
1+1
2+1
3+1
4+1
x+1
x+x+(x+1)
1+1+1+1
2+2+2+1
4+4+4+1
3+3+3+1
上面的一排和下面的一排各用了x根火柴棒,竖直方向用了(x+1)
根火柴棒,共用了【x+x+(x+1)】根火柴棒
新课讲解
…
第1个
4根
第100个
4根
新课讲解
①4+3(x-1);
②x+x+(x+1);
③1+3x;
④4x-(x-1)。
以后,为了方便表达与交流,通常会用像这样含有字母的式子来表示一些数学规律。(注意在这些式子中,我们要明确字母表示的意义)
由上我们知道,当用X来表示小正方形的个数时,火柴棒根数的计算方法有多种。
如:
新课讲解
做一做
…
根据你的计算方法,搭200个这样的正方形需要______根火柴棒.
用200代替[4+3(x-1)]中的x,可以得到4+3×(200-1)=601.
用200代替[x+x+(x+1)]中的x,可以得200+200+(200+1)=601.
议一议
在上面的活动中,我们借助字母描述了正方形的个数和火柴棒的根数之间的关系,你在以前的学习中有哪些地方用到了字母?这些字母都表示什么
用字母表示图形的面积公式
用字母表示数的运算律
新课讲解
加法的交换律可表示为
a+b=b+a;
加法的结合律可表示为
(a+b)+c=a+(b+c);
乘法的交换律可表示为
ab=ba;
乘法的结合律可表示为
(ab)c=a(bc);
乘法对加法的分配律可表示为
a(b+c) =ab+ac.
新课讲解
新课讲解
典例分析
例1.用含字母的式子填空:
(1)长方形的宽为4,长比宽多a,则长方形的长为______,面积为_________;
(2)一件衬衣的进价为a元,售价为2a元,则每件衬衣的利润为____元;
(3)一个数的相反数为a,则这个数是______;
(4)甲、乙两地相距s km,一辆汽车每小时行驶75 km,则它从甲地到乙地的行驶时间为____h.
4+a
16+4a
a
-a
① 数与字母、字母与字母相乘时省略乘号,数与字母相乘时数字在前;
② 出现多个字母时,字母按照26个字母顺序排列;
③ 相同字母相乘时应写成幂的形式;
④ 1或-1与字母相乘时,1通常省略不写;
⑤ 式子中出现除法运算时,一般按分数形式来写,带分数与字母相乘时,把带分数化成假分数.
字母表示数注意事项
100×t
100t
nm
mn
nn
n2
1n
n
n÷3
n
3
1
3
1 n
4n
3
新课讲解
新课讲解
典例分析
例2.用棋子摆成下列一组图案:
…
( 1 )
( 2 )
( 3 )
① 填写下表:
图案编号 (1) (2) (3) (4) (5) (10) (100)
棋子个数
② 摆第n个图案需要____个棋子.
3
6
9
12
15
30
300
3n
当堂小练
1.下列含有字母的式子符合书写规范的是( )
A.1a B.
C.0.5xy D.(x+y)÷z
当堂小练
2.明明步行上学,速度为V米/秒,亮亮骑自行车上学,速度是明明的3倍,则亮亮的速度可以表示为_______米/秒.
当堂小练
3.(双柏县)下面是一个简单的数值运算程序,当输入 的值为2时,输出的数值是 .
课堂小结
1、字母可以表示任何数;
2、用字母可以表示运算律和计算公式;
3、用字母可以把数和数量关系简明地表示出来,使复杂的问题简单化。
4、解决问题的方法:“从特殊到一般的寻求规律的方法”.“从不同角度观察思考探究问题”
第三章 整式及其加减
第1节 字母表示数
导入新课
讲授新课
课堂小结
随堂训练
学习目标
1.理解用字母表示数的意义.(重点)
2.能用字母表示以前学过的运算律和计算公式.
3.能用字母表示一些简单问题中的数量关系和变化规律.(难点)
新课引入
长方形的周长和面积:
正方形的周长和面积:
平行四边形的面积:
梯形的面积:
圆的周长和面积:
长方体的体积:
正方体的体积:
球的表面积和体积:
圆柱的体积:
圆锥的体积:
路程、速度、时间的关系:
新课引入
1只青蛙1张嘴,2只眼睛4条腿,扑通1声跳下水;
2只青蛙2张嘴,4只眼睛8条腿,扑通2声跳下水;
3只青蛙3张嘴, 6只眼睛12条腿,扑通3声跳下水;
………….
你觉得这首歌唱得完吗?
你能用数学知识,一句话把这首儿歌唱完吗?
接下来怎么唱?
合作探究
知识点1 用字母表示规律
新课讲解
十只青蛙____张嘴,____只眼睛____条腿,____声扑通跳下水;
一百只青蛙____张嘴,____只眼睛____条腿,____声扑通跳下水;
……
a只青蛙_____张嘴,_______只眼睛_______条腿,_______声扑通跳下水;
a
a
10
20
40
10
100
200
400
100
字母a表示什么?
字母可以表示数
新课讲解
用字母表示数的书写规则
① 数与字母、字母与字母相乘时省略乘号,数与字母相乘时数字在前;
② 出现多个字母时,字母按照26个字母顺序排列;
③ 相同字母相乘时应写成幂的形式;
④ 1或-1与字母相乘时,1通常省略不写;
⑤ 式子中出现除法运算时,一般按分数形式来写,带分数与字母相乘时,把带分数化成假分数.
如图所示,搭一个正方形需要4根火柴棒.
…
(1)按上面的方式,搭2个正方形需要__根火柴,搭3个正方形需要____根火柴.
(2)搭7个这样的正方形需要_____根火柴.
7
10
22
新课讲解
(3)搭100个这样的正方形需要多少根火柴
第1个
4根
第2个
第100个
3根
3根
…
有没有其他计算方法?
新课讲解
先摆 1根
第1个
3根
第100个
…
第2个
3根
3根
还可以这样
…
第1个
2根
第2个
2根
第100个
2根
2×100+(100+1)
还可以这样
新课讲解
…
第1个
4根
第100个
4根
…
还可以这样
新课讲解
(4)如果用x表示所搭正方形的个数, 那么搭x个这样的正方形需要多少根火柴
第1个
4根
第2个
第100个
3根
3根
…
新课讲解
先摆 1根
第1个
3根
第100个
…
第2个
3根
3根
或者这样
新课讲解
水平方向
2+2
3+3
4+4
第1个
第2个
第3个
第4个
…
第x个
x+x
1+1
竖直方向
1+1
2+1
3+1
4+1
x+1
x+x+(x+1)
1+1+1+1
2+2+2+1
4+4+4+1
3+3+3+1
上面的一排和下面的一排各用了x根火柴棒,竖直方向用了(x+1)
根火柴棒,共用了【x+x+(x+1)】根火柴棒
新课讲解
…
第1个
4根
第100个
4根
新课讲解
①4+3(x-1);
②x+x+(x+1);
③1+3x;
④4x-(x-1)。
以后,为了方便表达与交流,通常会用像这样含有字母的式子来表示一些数学规律。(注意在这些式子中,我们要明确字母表示的意义)
由上我们知道,当用X来表示小正方形的个数时,火柴棒根数的计算方法有多种。
如:
新课讲解
做一做
…
根据你的计算方法,搭200个这样的正方形需要______根火柴棒.
用200代替[4+3(x-1)]中的x,可以得到4+3×(200-1)=601.
用200代替[x+x+(x+1)]中的x,可以得200+200+(200+1)=601.
议一议
在上面的活动中,我们借助字母描述了正方形的个数和火柴棒的根数之间的关系,你在以前的学习中有哪些地方用到了字母?这些字母都表示什么
用字母表示图形的面积公式
用字母表示数的运算律
新课讲解
加法的交换律可表示为
a+b=b+a;
加法的结合律可表示为
(a+b)+c=a+(b+c);
乘法的交换律可表示为
ab=ba;
乘法的结合律可表示为
(ab)c=a(bc);
乘法对加法的分配律可表示为
a(b+c) =ab+ac.
新课讲解
新课讲解
典例分析
例1.用含字母的式子填空:
(1)长方形的宽为4,长比宽多a,则长方形的长为______,面积为_________;
(2)一件衬衣的进价为a元,售价为2a元,则每件衬衣的利润为____元;
(3)一个数的相反数为a,则这个数是______;
(4)甲、乙两地相距s km,一辆汽车每小时行驶75 km,则它从甲地到乙地的行驶时间为____h.
4+a
16+4a
a
-a
① 数与字母、字母与字母相乘时省略乘号,数与字母相乘时数字在前;
② 出现多个字母时,字母按照26个字母顺序排列;
③ 相同字母相乘时应写成幂的形式;
④ 1或-1与字母相乘时,1通常省略不写;
⑤ 式子中出现除法运算时,一般按分数形式来写,带分数与字母相乘时,把带分数化成假分数.
字母表示数注意事项
100×t
100t
nm
mn
nn
n2
1n
n
n÷3
n
3
1
3
1 n
4n
3
新课讲解
新课讲解
典例分析
例2.用棋子摆成下列一组图案:
…
( 1 )
( 2 )
( 3 )
① 填写下表:
图案编号 (1) (2) (3) (4) (5) (10) (100)
棋子个数
② 摆第n个图案需要____个棋子.
3
6
9
12
15
30
300
3n
当堂小练
1.下列含有字母的式子符合书写规范的是( )
A.1a B.
C.0.5xy D.(x+y)÷z
当堂小练
2.明明步行上学,速度为V米/秒,亮亮骑自行车上学,速度是明明的3倍,则亮亮的速度可以表示为_______米/秒.
当堂小练
3.(双柏县)下面是一个简单的数值运算程序,当输入 的值为2时,输出的数值是 .
课堂小结
1、字母可以表示任何数;
2、用字母可以表示运算律和计算公式;
3、用字母可以把数和数量关系简明地表示出来,使复杂的问题简单化。
4、解决问题的方法:“从特殊到一般的寻求规律的方法”.“从不同角度观察思考探究问题”
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
