直线和平面平行
图片预览








文档简介
课件69张PPT。高二年级 数学
第九章 第一节空间的平行直线 与异面直线 (一)
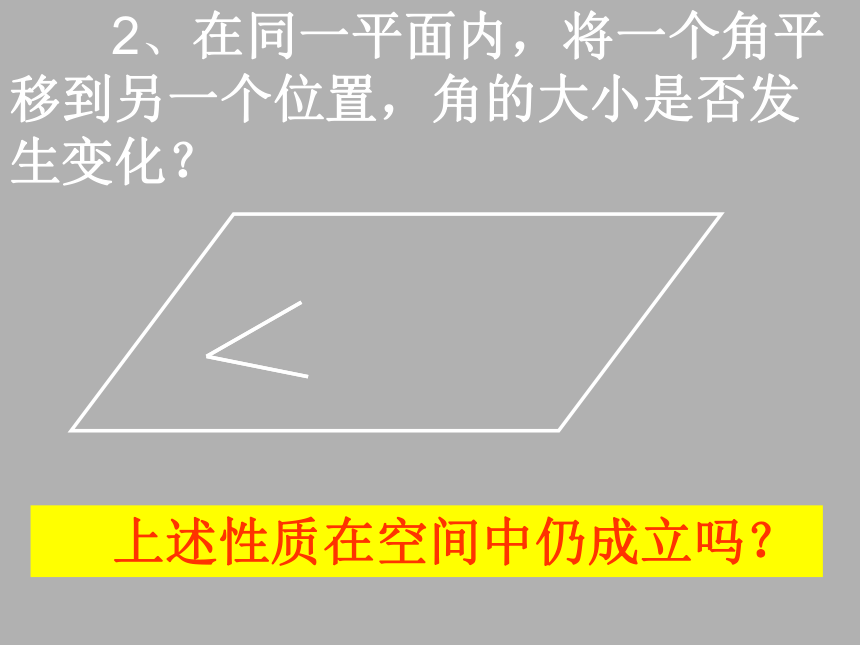
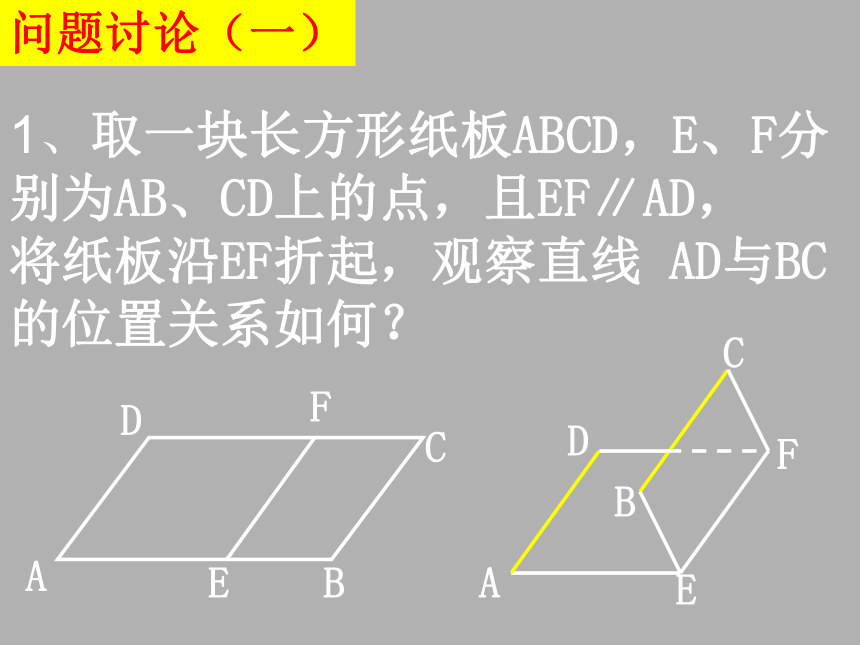
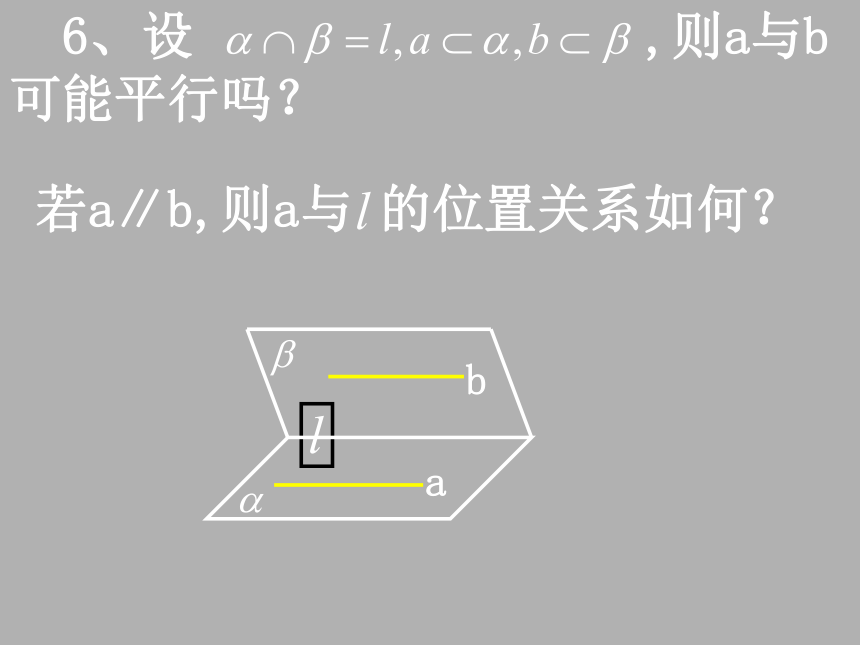
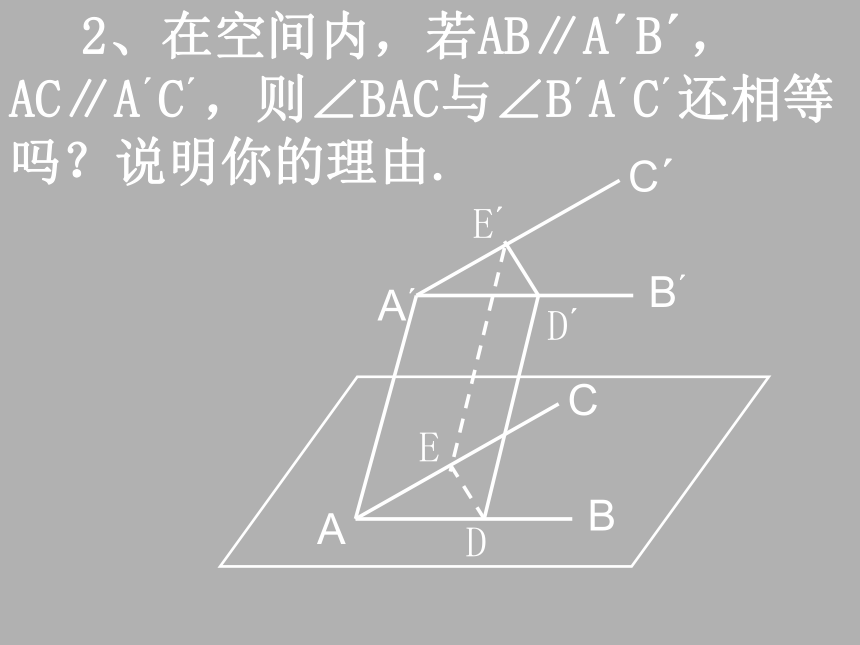
问题提出 1、在同一平面内,若直线a、b都平行于直线c,则a、b的位置关系如何?上述性质在空间中仍成立吗? 2、在同一平面内,将一个角平移到另一个位置,角的大小是否发生变化? 上述性质在空间中仍成立吗? 空间的平行直线与异面直线 (1)1、取一块长方形纸板ABCD,E、F分别为AB、CD上的点,且EF∥AD, 将纸板沿EF折起,观察直线 AD与BC的位置关系如何?问题讨论(一) 2、设直线a∥直线b,将直线a在空间作平行移动,在平移过程中a与b仍保持平行吗? 3、通过上述实验,可得什么结论? 公理4 平行于同一条直线的两条直线互相平行推理模式:设a、b、c为直线,则 5、过直线外一点,可作几条直线与已知直线平行?为什么? 6、设 ,则a与b可能平行吗? 若a∥b,则a与 的位置关系如何?问题讨论(二) 1、在同一平面内,若AB∥A′B′,AC∥A′C′,则∠BAC与∠B′A′C′的大小关系如何? 2、在空间内,若AB∥A′B′,AC∥A′C′,则∠BAC与∠B′A′C′还相等吗?说明你的理由.(3)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等. 讲解新课 分析:在平面内,这个结论我们已经证明成立了.在空间中,这个结论是否成立,还需通过证明. 要证明两个角相等,常用的方法有:证明两个三角形全等或相似,则对应角相等;证明两直线平行,则同位角、内错角相等;证明平行四边形,则它的对角相等,等等.DD′EE′→等角定理演示(3)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等. 讲解新课 DD′EE′并且方向相同. 求证: (3)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等. 讲解新课 DD′EE′并且方向相同. 求证: 3、根据上述分析,可得什么结论? 定理 如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等.如果空间图形的所有点E都沿同一方向移动相同的距离到F则就说点F在空间做了一次平移由上述定理可知,图形平移后与原图形全等,即对应角和对应两点间的距离保持不变,上述定理表明角平移后大小不变 4、在空间中,如果一个角的两边和另一个角的两边都不平行,那么这两个角一定不相等吗? 5、如果两条相交直线分别平行另外两条相交直线,则这两组相交直线的夹角的大小关系如何?推论: 如果两条相交直线和另两条相交直线分别平行, 那么这两组直线所成的锐角(或直角)相等.判断下列命题的真假,真的打“√”,假的打“×”
1.平行于同一直线的两条直线平行( )
2.垂直于同一直线的两条直线平行( )
3.过直线外一点,有且只有一条
直线与已知直线平行( )
4.与已知直线平行且距离等于定
长的直线只有两条( )
5.若一个角的两边分别与另一个
角的两边平行,那么这两个角相等( )
6.若两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等( )√√√×××课堂练习 课堂练习 √巩固练习 例1、已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,求证;四边形EFGH是平行四边形.顺次连接不共面的四点所组成
的四边形叫做空间四边形
相对定点的连线叫做空间四边
形的对角线 讲解范例 例2 已知四边形ABCD是空间四边形,E、H分别是AB、AD的中点,F、G分别是边CB、CD上的点,且 求证:四边形EFGH是梯形. 证明:如图,连接BD根据公理4,EH//FG又FG>EH,∴四边形EFGH的一组对边平行但不相等 ∴四边形EFGH是梯形. 例3、在长方体ABCD-A1B1C1D1中,求证:△AB1C∽△C1A1D.异 面 直 线练 习1、在空间一个角的两边和另一个角的两边平行,则这两个角( )
A、相等
B 、互补
C、相等或互补
D、互余
问题讨论(一) 1. 任意两条相交直线或平行直线共面吗? 2. 将两条相交直线拉开后,它们还相交吗?平行吗?共面吗? 3. 将上述两直线取名为异面直线,那么,异面直线与相交直线、平行直线的本质区别在哪里? 4、怎样定义异面直线? 不同在任何一个平面内的两条直线叫做异面直线1.空间两直线的位置关系 (1)相交——有且只有一个公共点;(2)平行——在同一平面内,没有公共点;(3)异面——不在任何一个平面内,没有公共点. ab复习引入 新授内容 1. 两条异面直线的画法abB2.判断异面直线的方法:连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线. alABα推理模式: 6、连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线吗?为什么? 问题讨论(二) 1. 两异面直线之间有一个相对倾斜度,若将两异面直线分别平行移动,它们的相对倾斜度是否发生变化? 2. 两异面直线的相对倾斜度,可通过一个什么样的角来反映?新授内容 3. 异面直线bOOb′所成的角异面直线所成的角的范围: a 'b 'ba ' 6、两异面直线的夹角的取值范围用一个区间怎样表示? 如果两条异面直线所成的角是直角,则叫两条异面直线垂直.两条异面直线a,b 垂直,记作a⊥b. 5.两条异面直线的公垂线、距离 和两条异面直线都垂直相交的直线,我们称之为异面直线的公垂线. 公垂线段的长度,叫做两条异面直线间的距离. 两条异面直线的公垂线在这两条异面直线间的线段叫做公垂线段. 新授内容 4.异面直线垂直: 8、在平面内,垂直于同一条直线的两直线的位置关系如何?在空间呢?1.一条直线与两条异面直线中的一条相
交,那么它与另一条之间的位置关系
是( )
A.平行 B.相交 C.异面
D.可能平行、可能相交、可能异面巩固练习 D2.设a、b、c是空间三条直线,下面给出
四个命题:
①如果a⊥b,b⊥c,则a∥c;
②如果a、b是异面直线,b、c是异面直线,
则a、c也是异面直线;
③如果a和b相交,b和c相交,则a和c也相
交;
④如果a和b共面,b和c共面,则a和c也共
面。
那么上述命题中,真命题的个数是( )
A、4 B、3 C、2 D、1 E、0E巩固练习 3.下列命题中,其中正确的个数有 。
(1)若两条直线没有公共点,则这两条直线
互相平行
(2)若两条直线都和第三条直线相交,则这
两条直线互相平行
(3)若两条直线都和第三条直线平行,则这
两条直线互相平行
(4)若两条直线都和第三条直线异面,则这
两条直线互相平行1个巩固练习4. 两条直线不相交是这两条直线异面的
条件
必要不充分巩固练习课堂练习 判断题(对的打“√”,错的打“×”)
(1)垂直于两条异面直线的直线有且只有一条( )
(2)在正方体中,相邻两侧面的一对异面的对角线所成的角为60o( )
(3)四边形的一边不可能既和它的邻边垂直,又和它的对边垂直( )×√×练习 判断下列命题是否正确? 1、过直线外一点,有且只有一条直线与这条直线平行. 2、过一点有且只有一条直线与已知直线垂直.(×)(√) 3、分别在两个平面内的两直线一定是异面直线.(×) 4、若直线a在平面α内,直线b不在平面α内,则a,b是异面直线.(×) 5、若直线a与两条平行线中的一条是异面直线,则它和另一条也是异面直线.(×)1. 两条异面直线指的是 ( )
A.没有公共点的两条直线,
B.分别位于两个不同平面内的两条直线,
C.某一个平面内的一条直线和这个平面
外的一条直线,
D.不同在任何一个平面内的两条直线.D练 习2. 已知 a、b 是异面直线,直线c//a,
那么 c 与 b ( )
A.一定是异面直线
B.一定是相交直线
C.不可能是平行直线
D.不可能是相交直线 C 练 习3. 两条直线不平行是这两条直线异面的
( )
A.充分必要条件,
B.充分不必要条件,
C.必要不充分条件,
D.既不充分又不必要条件. C 练 习4. 直线a、b是异面直线,a α,b β,
且α∩β= c,则 ( )
A. c与 a、b都不相交
B. c与 a、b都相交
C. c至少与 a、b中的一条相交
D. c至多与 a、b中的一条相交 C 练 习7.给出下面四个命题:
(1)在空间,过直线外一点作这直线的平行
线只能有一条;
(2)既不平行又不相交的两条直线是异面直线;
(3)两两互相平行的三条直线确定3个平面;
(4)不可能在同一平面内的两条直线是异面直线.
其中正确命题的个数是( )
A.1. B. 2. C. 3. D. 4.C8.若直线a、b与直线l 相交成等角,则 a、b的位置关系是( )
A.异面 B.平行 C.相交
D.可能相交,可能平行,也可能异面9.如果a、b是异面直线,直线c与a、b都相 交,那么由这三条直线中的两条所确定的平面共有 个.D2 10、填空: 1)、设直线a,b在平面α内的射影为a′,b′,若a′∥b′,则直线a,b的位置关系是____________平行或异面讲解范例: 解:(l) (2) ∵CC1∥BB1∴BA1和BB1所成的锐角就是BA1和CC1所成的角. ∵∠A1BB1=45° ∴BA1和CC1所成的角是45°.讲解范例: 解:(3) ∵AB⊥AA1,AB∩AA1=A, AB⊥BC,AB∩BC=B, ∴AB是BC和AA1的公垂线段 ∵AB=a, ∴BC和AA1的距离是a .讲解范例: 例2 在正方体ABCD-A1B1C1D1中,求:
(1)A1B与B1D1所成角; (2)AC与BD1所成角. 解:(1) 如图,连结BD,A1D, ∵ABCD-A1B1C1D1是正方体, ∴DD1//BB1且DD1=BB1. ∴四边形DBB1D1为平行四边形, ∴BD//B1D1. ∵ A1B,BD,A1D是全等的正方形的对角线 ∴A1B=BD=A1D,△A1BD是正三角形,∴∠A1BD=60o,∵∠A1BD是锐角,∴∠A1BD是异面直线A1B与B1D1所成的角.∴A1B与B1D1成角为60o.讲解范例: 例2 在正方体ABCD-A1B1C1D1中,求:
(1)A1B与B1D1所成角; (2)AC与BD1所成角. 解:(2) OE连BD交AC于O, 取DD1 中点E, 连EO, EA,EC. ∵O为BD中点,∴OE//BD1.连 EA,EC. ∵∠EDA=∠EDC=90o,ED=ED,AD=DC, ∴△EDA≌△EDC, ∴EA=EC. ∴EO⊥AC,∴∠EOA=90o.∴∠EOA是异面直线AC与BD1所成角, ∴AC与BD成角90o. 2)、已知两异面直线a、b所成的角为60°,直线 与a、b所成的角都等于θ,则θ的取值范围是_______知识回顾 公理4 平行于同一条直线的两条直线互相平行 1、三线平行公理 2、等角定理 定理 如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等. 3、异面直线的定义 不同在任何一个平面内的两条直线叫做异面直线 4、异面直线的夹角 设a、b为两异面直线,经过空间 一点o作直线 ,把 所成的锐角(或直角)叫做异面直线 a与b所成的角(或夹角).例题分析 例1、如图,点E、F、M、N分别是正方体的四条棱的中点,判断直线EF和MN是否为异面直线? 例5、在正方体ABCD-A1B1C1D1中,M是A1C1的中点,N是B1C1的中点,求异面直线AM与CN所成的角. 例7、在长方体ABCD-A1B1C1D1中,BC=a,CD=b,DD1=c(b>a),求异面直线A1C与B1D1所成的角. OE 例3、在四面体ABCD中,E、F分别是AD、BC上的点,且 ,
已知AB=CD=3,EF= ,求异面直线AB和CD所成的角.M 例6、如图,在四面体ABCD中, △ABC是正三角形,AD=BD=CD,∠ADB=∠BDC=∠CDA=90°,M、N分别是AB和CD的中点,求异面直线DM与BN所成的角. O
第九章 第一节空间的平行直线 与异面直线 (一)
问题提出 1、在同一平面内,若直线a、b都平行于直线c,则a、b的位置关系如何?上述性质在空间中仍成立吗? 2、在同一平面内,将一个角平移到另一个位置,角的大小是否发生变化? 上述性质在空间中仍成立吗? 空间的平行直线与异面直线 (1)1、取一块长方形纸板ABCD,E、F分别为AB、CD上的点,且EF∥AD, 将纸板沿EF折起,观察直线 AD与BC的位置关系如何?问题讨论(一) 2、设直线a∥直线b,将直线a在空间作平行移动,在平移过程中a与b仍保持平行吗? 3、通过上述实验,可得什么结论? 公理4 平行于同一条直线的两条直线互相平行推理模式:设a、b、c为直线,则 5、过直线外一点,可作几条直线与已知直线平行?为什么? 6、设 ,则a与b可能平行吗? 若a∥b,则a与 的位置关系如何?问题讨论(二) 1、在同一平面内,若AB∥A′B′,AC∥A′C′,则∠BAC与∠B′A′C′的大小关系如何? 2、在空间内,若AB∥A′B′,AC∥A′C′,则∠BAC与∠B′A′C′还相等吗?说明你的理由.(3)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等. 讲解新课 分析:在平面内,这个结论我们已经证明成立了.在空间中,这个结论是否成立,还需通过证明. 要证明两个角相等,常用的方法有:证明两个三角形全等或相似,则对应角相等;证明两直线平行,则同位角、内错角相等;证明平行四边形,则它的对角相等,等等.DD′EE′→等角定理演示(3)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等. 讲解新课 DD′EE′并且方向相同. 求证: (3)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等. 讲解新课 DD′EE′并且方向相同. 求证: 3、根据上述分析,可得什么结论? 定理 如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等.如果空间图形的所有点E都沿同一方向移动相同的距离到F则就说点F在空间做了一次平移由上述定理可知,图形平移后与原图形全等,即对应角和对应两点间的距离保持不变,上述定理表明角平移后大小不变 4、在空间中,如果一个角的两边和另一个角的两边都不平行,那么这两个角一定不相等吗? 5、如果两条相交直线分别平行另外两条相交直线,则这两组相交直线的夹角的大小关系如何?推论: 如果两条相交直线和另两条相交直线分别平行, 那么这两组直线所成的锐角(或直角)相等.判断下列命题的真假,真的打“√”,假的打“×”
1.平行于同一直线的两条直线平行( )
2.垂直于同一直线的两条直线平行( )
3.过直线外一点,有且只有一条
直线与已知直线平行( )
4.与已知直线平行且距离等于定
长的直线只有两条( )
5.若一个角的两边分别与另一个
角的两边平行,那么这两个角相等( )
6.若两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等( )√√√×××课堂练习 课堂练习 √巩固练习 例1、已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,求证;四边形EFGH是平行四边形.顺次连接不共面的四点所组成
的四边形叫做空间四边形
相对定点的连线叫做空间四边
形的对角线 讲解范例 例2 已知四边形ABCD是空间四边形,E、H分别是AB、AD的中点,F、G分别是边CB、CD上的点,且 求证:四边形EFGH是梯形. 证明:如图,连接BD根据公理4,EH//FG又FG>EH,∴四边形EFGH的一组对边平行但不相等 ∴四边形EFGH是梯形. 例3、在长方体ABCD-A1B1C1D1中,求证:△AB1C∽△C1A1D.异 面 直 线练 习1、在空间一个角的两边和另一个角的两边平行,则这两个角( )
A、相等
B 、互补
C、相等或互补
D、互余
问题讨论(一) 1. 任意两条相交直线或平行直线共面吗? 2. 将两条相交直线拉开后,它们还相交吗?平行吗?共面吗? 3. 将上述两直线取名为异面直线,那么,异面直线与相交直线、平行直线的本质区别在哪里? 4、怎样定义异面直线? 不同在任何一个平面内的两条直线叫做异面直线1.空间两直线的位置关系 (1)相交——有且只有一个公共点;(2)平行——在同一平面内,没有公共点;(3)异面——不在任何一个平面内,没有公共点. ab复习引入 新授内容 1. 两条异面直线的画法abB2.判断异面直线的方法:连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线. alABα推理模式: 6、连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线吗?为什么? 问题讨论(二) 1. 两异面直线之间有一个相对倾斜度,若将两异面直线分别平行移动,它们的相对倾斜度是否发生变化? 2. 两异面直线的相对倾斜度,可通过一个什么样的角来反映?新授内容 3. 异面直线bOOb′所成的角异面直线所成的角的范围: a 'b 'ba ' 6、两异面直线的夹角的取值范围用一个区间怎样表示? 如果两条异面直线所成的角是直角,则叫两条异面直线垂直.两条异面直线a,b 垂直,记作a⊥b. 5.两条异面直线的公垂线、距离 和两条异面直线都垂直相交的直线,我们称之为异面直线的公垂线. 公垂线段的长度,叫做两条异面直线间的距离. 两条异面直线的公垂线在这两条异面直线间的线段叫做公垂线段. 新授内容 4.异面直线垂直: 8、在平面内,垂直于同一条直线的两直线的位置关系如何?在空间呢?1.一条直线与两条异面直线中的一条相
交,那么它与另一条之间的位置关系
是( )
A.平行 B.相交 C.异面
D.可能平行、可能相交、可能异面巩固练习 D2.设a、b、c是空间三条直线,下面给出
四个命题:
①如果a⊥b,b⊥c,则a∥c;
②如果a、b是异面直线,b、c是异面直线,
则a、c也是异面直线;
③如果a和b相交,b和c相交,则a和c也相
交;
④如果a和b共面,b和c共面,则a和c也共
面。
那么上述命题中,真命题的个数是( )
A、4 B、3 C、2 D、1 E、0E巩固练习 3.下列命题中,其中正确的个数有 。
(1)若两条直线没有公共点,则这两条直线
互相平行
(2)若两条直线都和第三条直线相交,则这
两条直线互相平行
(3)若两条直线都和第三条直线平行,则这
两条直线互相平行
(4)若两条直线都和第三条直线异面,则这
两条直线互相平行1个巩固练习4. 两条直线不相交是这两条直线异面的
条件
必要不充分巩固练习课堂练习 判断题(对的打“√”,错的打“×”)
(1)垂直于两条异面直线的直线有且只有一条( )
(2)在正方体中,相邻两侧面的一对异面的对角线所成的角为60o( )
(3)四边形的一边不可能既和它的邻边垂直,又和它的对边垂直( )×√×练习 判断下列命题是否正确? 1、过直线外一点,有且只有一条直线与这条直线平行. 2、过一点有且只有一条直线与已知直线垂直.(×)(√) 3、分别在两个平面内的两直线一定是异面直线.(×) 4、若直线a在平面α内,直线b不在平面α内,则a,b是异面直线.(×) 5、若直线a与两条平行线中的一条是异面直线,则它和另一条也是异面直线.(×)1. 两条异面直线指的是 ( )
A.没有公共点的两条直线,
B.分别位于两个不同平面内的两条直线,
C.某一个平面内的一条直线和这个平面
外的一条直线,
D.不同在任何一个平面内的两条直线.D练 习2. 已知 a、b 是异面直线,直线c//a,
那么 c 与 b ( )
A.一定是异面直线
B.一定是相交直线
C.不可能是平行直线
D.不可能是相交直线 C 练 习3. 两条直线不平行是这两条直线异面的
( )
A.充分必要条件,
B.充分不必要条件,
C.必要不充分条件,
D.既不充分又不必要条件. C 练 习4. 直线a、b是异面直线,a α,b β,
且α∩β= c,则 ( )
A. c与 a、b都不相交
B. c与 a、b都相交
C. c至少与 a、b中的一条相交
D. c至多与 a、b中的一条相交 C 练 习7.给出下面四个命题:
(1)在空间,过直线外一点作这直线的平行
线只能有一条;
(2)既不平行又不相交的两条直线是异面直线;
(3)两两互相平行的三条直线确定3个平面;
(4)不可能在同一平面内的两条直线是异面直线.
其中正确命题的个数是( )
A.1. B. 2. C. 3. D. 4.C8.若直线a、b与直线l 相交成等角,则 a、b的位置关系是( )
A.异面 B.平行 C.相交
D.可能相交,可能平行,也可能异面9.如果a、b是异面直线,直线c与a、b都相 交,那么由这三条直线中的两条所确定的平面共有 个.D2 10、填空: 1)、设直线a,b在平面α内的射影为a′,b′,若a′∥b′,则直线a,b的位置关系是____________平行或异面讲解范例: 解:(l) (2) ∵CC1∥BB1∴BA1和BB1所成的锐角就是BA1和CC1所成的角. ∵∠A1BB1=45° ∴BA1和CC1所成的角是45°.讲解范例: 解:(3) ∵AB⊥AA1,AB∩AA1=A, AB⊥BC,AB∩BC=B, ∴AB是BC和AA1的公垂线段 ∵AB=a, ∴BC和AA1的距离是a .讲解范例: 例2 在正方体ABCD-A1B1C1D1中,求:
(1)A1B与B1D1所成角; (2)AC与BD1所成角. 解:(1) 如图,连结BD,A1D, ∵ABCD-A1B1C1D1是正方体, ∴DD1//BB1且DD1=BB1. ∴四边形DBB1D1为平行四边形, ∴BD//B1D1. ∵ A1B,BD,A1D是全等的正方形的对角线 ∴A1B=BD=A1D,△A1BD是正三角形,∴∠A1BD=60o,∵∠A1BD是锐角,∴∠A1BD是异面直线A1B与B1D1所成的角.∴A1B与B1D1成角为60o.讲解范例: 例2 在正方体ABCD-A1B1C1D1中,求:
(1)A1B与B1D1所成角; (2)AC与BD1所成角. 解:(2) OE连BD交AC于O, 取DD1 中点E, 连EO, EA,EC. ∵O为BD中点,∴OE//BD1.连 EA,EC. ∵∠EDA=∠EDC=90o,ED=ED,AD=DC, ∴△EDA≌△EDC, ∴EA=EC. ∴EO⊥AC,∴∠EOA=90o.∴∠EOA是异面直线AC与BD1所成角, ∴AC与BD成角90o. 2)、已知两异面直线a、b所成的角为60°,直线 与a、b所成的角都等于θ,则θ的取值范围是_______知识回顾 公理4 平行于同一条直线的两条直线互相平行 1、三线平行公理 2、等角定理 定理 如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等. 3、异面直线的定义 不同在任何一个平面内的两条直线叫做异面直线 4、异面直线的夹角 设a、b为两异面直线,经过空间 一点o作直线 ,把 所成的锐角(或直角)叫做异面直线 a与b所成的角(或夹角).例题分析 例1、如图,点E、F、M、N分别是正方体的四条棱的中点,判断直线EF和MN是否为异面直线? 例5、在正方体ABCD-A1B1C1D1中,M是A1C1的中点,N是B1C1的中点,求异面直线AM与CN所成的角. 例7、在长方体ABCD-A1B1C1D1中,BC=a,CD=b,DD1=c(b>a),求异面直线A1C与B1D1所成的角. OE 例3、在四面体ABCD中,E、F分别是AD、BC上的点,且 ,
已知AB=CD=3,EF= ,求异面直线AB和CD所成的角.M 例6、如图,在四面体ABCD中, △ABC是正三角形,AD=BD=CD,∠ADB=∠BDC=∠CDA=90°,M、N分别是AB和CD的中点,求异面直线DM与BN所成的角. O
